Е. В. Бурлаченко
ДВЕ АЛГЕБРЫ И СВОЙСТВА НАТУРАЛЬНЫХ ЧИСЕЛ
1
Будем рассматривать
формальный степенной ряд с действительными коэффициентами как
последовательность этих коэффициентов, т.е. как элемент векторного
пространства. Обозначим:

Базис
пространства, в котором координаты каждой последовательности (т.е. коэффициенты
разложения по базисным векторам) совпадают с ее значениями, назовем основным.
Каждой матрице ![]() поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы
поставим в
соответствие преобразование, отоброжающее последовательность векторов основного
базиса на последовательность столбцов матрицы ![]() . Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Образ вектора
. Матрицу и соответствующее ей преобразование будем
обозначать одним и тем же символом. Столбцы и строки матрицы пронумеруем целыми
неотрицательными числами. Образ вектора ![]() при
преобразовании
при
преобразовании ![]() обозначим
обозначим ![]() .
.
Целые
неотрицательные числа будем обозначать буквами ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , целые числа – буквой
, целые числа – буквой
![]() , действительные числа – буквами
, действительные числа – буквами ![]() ,
, ![]() ,
, ![]() .
.
Произведением ![]() назовем вектор
назовем вектор ![]() , где
, где
 .
.
Матрицу
вида ![]() (
( ![]() -й член
-й член ![]() -го столбца матрицы равен
-го столбца матрицы равен ![]() и нулю при
и нулю при ![]() ) назовем матрицей умножения на вектор
) назовем матрицей умножения на вектор ![]() .
.
Обратным
к ![]() назовем вектор
назовем вектор 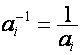 , определяемый уравнением
, определяемый уравнением
![]() .
.
Вектор
![]()
назовем ![]() -й степенью
-й степенью ![]() .
. ![]() -й вектор основного базиса представим как
-й вектор основного базиса представим как ![]() -ю степень
-ю степень ![]() . Каждый вектор запишется в виде
. Каждый вектор запишется в виде
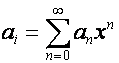 .
.
![]() -й столбец матрицы
-й столбец матрицы ![]() принимает вид
принимает вид ![]() . Сама матрица умножения представима в виде
. Сама матрица умножения представима в виде
 .
.
Матрицу,
![]() -й столбец которой является
-й столбец которой является ![]() -й степенью
-й степенью ![]() , назовем матрицей
степеней вектора
, назовем матрицей
степеней вектора ![]() и обозначим
и обозначим ![]() . Например,
. Например,
 ,
,  ,
,  ;
;
 ,
,  .
.
Так как
![]() ,
,
то
![]() .
.
Например,
 ,
,
т.е.
![]() .
.
Таким образом, матрица степеней отображает
произведение векторов на произведение их образов:
![]() ,
,
так что
![]() .
.
Если рассматривать ![]() и
и ![]() как функции
как функции ![]() и
и ![]() , то выражению
, то выражению ![]() соответствует
подстановка
соответствует
подстановка ![]() .
.
Обозначим:
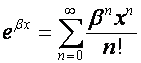 .
.
Убедимся, что векторы данного вида умножаются по
правилу
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Обозначим:
![]() ,
,
так что
![]() .
.
Пусть ![]() – элемент
матрицы
– элемент
матрицы ![]() , где
, где ![]() – номер строки,
– номер строки, ![]() – номер столбца. Тогда
– номер столбца. Тогда
![]()

 ,
,
где ![]() – комплексные числа.
Так как все члены вектора
– комплексные числа.
Так как все члены вектора ![]() , начиная с
, начиная с ![]() -го, равны нулю, то
-го, равны нулю, то ![]() . Таким образом,
. Таким образом,
 .
.
Вектор
![]() ,
, ![]() ,
,
назовем ![]() -й степенью
-й степенью ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Первый
столбец матрицы ![]() обозначим
обозначим ![]() . Вектор
. Вектор ![]() ,
, ![]() , назовем логарифмом вектора
, назовем логарифмом вектора ![]() и обозначим
и обозначим ![]() ; вектор
; вектор ![]() , где
, где ![]() произвольно, назовем
экспонентой вектора
произвольно, назовем
экспонентой вектора ![]() и обозначим
и обозначим ![]() . Так как
. Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Так как
![]()
![]() ,
,
то
![]() .
.
Диагональную
матрицу, диагональные элементы которой равны значениям вектора ![]() , обозначим
, обозначим ![]() :
:
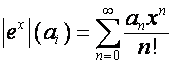 ,
, 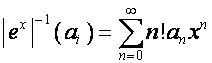 .
.
![]() -ю строку матрицы
-ю строку матрицы
![]()
обозначим ![]() . Так как
. Так как
![]() ,
,
то
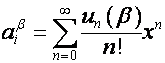 .
.
Например, если ![]() , то
, то
![]() .
.
Пусть ![]() и
и ![]() – преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
– преобразования,
соответствующие дифференцированию и интегрированию в алгебре формальных
степенных рядов:
 ,
,
где знак * означает транспонирование,
 .
.
Обозначим:
![]() ,
, ![]() .
.
Убедимся, что
![]() ,
,
или
![]() :
:
 .
.
Следовательно,
![]() ,
,
![]() ,
,
или
![]() .
.
Так как
![]() ,
,
то
![]() ,
,
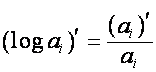 .
.
Отсюда находим:
 .
.
2
Эйлер первым из математиков обнаружил, что
некоторые свойства натуральных чисел, плохо различимые в рамках теории чисел,
становятся зримей при обращении к алгебре формальных степенных рядов.
Простое число имеет два делителя – единицу
и самого себя. Если считать это определением, то единица не является простым
числом. Распределение простых чисел не подчиняется строгому закону, но Эйлер
открыл, что последовательность сумм делителей натуральных чисел является
реккурентной, т.е. такой, каждый член которой по определенному правилу
вычисляется по предыдущим членам. Его мемуар «Открытие наиболее необычайного
закона чисел, относящегося к суммам их делителей» можно найти в [1, стр.112].
Изучая разбиения натуральных чисел, Эйлер
придумал метод производящих функций, суть которого в том, что алгоритм
получения искомых комбинаторных величин связывается с алгоритмом операции
умножения в алгебре формальных степенных рядов. Отсюда, например, видно, что
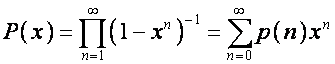 ,
,
где ![]() ,
, ![]() – число всевозможных
разбиений числа
– число всевозможных
разбиений числа ![]() на слагаемые, т.е.
число решений в неотрицательных целых числах уравнения
на слагаемые, т.е.
число решений в неотрицательных целых числах уравнения
![]() .
.
Раскладывая
обратный ряд по степеням ![]() , находим:
, находим:
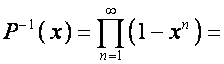
![]()
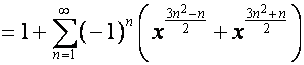 .
.
Доказательство
вытекает из другого равенства [2. стр.138]:
 ,
,
где ![]() – число разбиений
– число разбиений ![]() на четное число
неравных слагаемых,
на четное число
неравных слагаемых, ![]() – число разбиений
– число разбиений ![]() на нечетное число
неравных слагаемых.
на нечетное число
неравных слагаемых.
Таким образом,
![]()
Последовательность слагаемых обрывается, как только
число, стоящее под знаком ![]() , становится отрицательным.
, становится отрицательным.
Следуя Эйлеру, прологарифмируем ряд ![]() , продифференцируем полученный результат и домножим на
, продифференцируем полученный результат и домножим на ![]() :
:
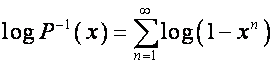 ,
,
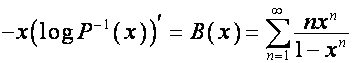 .
.
Разлагая каждый член суммы 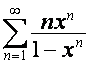 в геометрическую прогрессию,
получаем:
в геометрическую прогрессию,
получаем:
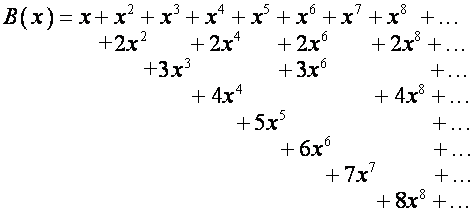
«Мы легко здесь
находим, – заключает Эйлер, – что каждая
степень ![]() встречается столько
раз, сколько ее показатель имеет делителей, и что каждый делитель появляется в
качестве коэффициента при той же самой степени
встречается столько
раз, сколько ее показатель имеет делителей, и что каждый делитель появляется в
качестве коэффициента при той же самой степени ![]() . Следовательно, если мы соберем члены с одинаковыми
степенями, то коэффициент при каждой степени
. Следовательно, если мы соберем члены с одинаковыми
степенями, то коэффициент при каждой степени ![]() будет суммой делителей
показателя степени». Таким образом,
будет суммой делителей
показателя степени». Таким образом,
 ,
,
где ![]() – сумма делителей
числа
– сумма делителей
числа ![]() .
.
С другой стороны,
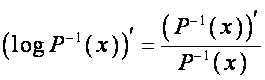 .
.
Пользуясь
разложением ![]() по степеням
по степеням ![]() , получаем
, получаем
 ,
,
![]() .
.
Отсюда
выводим:
![]()
Последовательность слагаемых обрывается, как только
число, стоящее под знаком ![]() , становится отрицательным; если появляется символ
, становится отрицательным; если появляется символ ![]() , он заменяется числом
, он заменяется числом
![]() .
.
Формальный ряд

называется рядом Дирихле [3. стр.144]. На множестве
рядов Дирихле задается операция умножения:
 ,
,
где
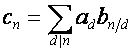 ,
,
символ ![]() означает, что
суммирование ведется по всем делителям числа
означает, что
суммирование ведется по всем делителям числа ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Определенное
таким образом умножение коммутативно и ассоциативно.
Отображение  переводит алгебру
рядов Дирихле в изоморфную ей алгебру, заданную на множестве формальных
степенных рядов вида
переводит алгебру
рядов Дирихле в изоморфную ей алгебру, заданную на множестве формальных
степенных рядов вида
 .
.
Умножение
задается матрицей
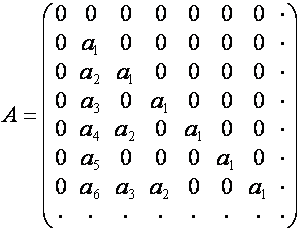 ,
,
![]() -й столбец которой,
-й столбец которой, ![]() , имеет вид
, имеет вид ![]() . Как видим, это то самое преобразование, которым пользовался
Эйлер для нахождения ряда
. Как видим, это то самое преобразование, которым пользовался
Эйлер для нахождения ряда ![]() : если первый столбец матрицы
: если первый столбец матрицы ![]() – ряд
– ряд ![]() , то
, то
![]() .
.
3
На множестве векторов

зададим
операцию ![]() - умножения:
- умножения:
![]() ,
,
где
 .
.
![]() -й столбец матрицы имеет вид
-й столбец матрицы имеет вид
![]() , так что
, так что
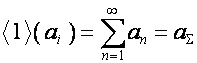 .
.
Для обращения с величинами ![]() и
и ![]() можно ввести
непротиворечивые правила, но нам это без надобности.
можно ввести
непротиворечивые правила, но нам это без надобности.
Так как
![]() ,
,
то
 .
.
![]() -обратным к
-обратным к ![]() назовем вектор
назовем вектор ![]() , определяемый равенством
, определяемый равенством
![]() .
.
Это
согласуется с тем, что ![]() – единичная матрица.
Обозначим
– единичная матрица.
Обозначим
![]() .
.
Для краткости алгебру формальных степенных
рядов будем называть ![]() - алгеброй, алгебру, задаваемую матрицами
- алгеброй, алгебру, задаваемую матрицами ![]() , –
, – ![]() -алгеброй. Проследим аналогию:
-алгеброй. Проследим аналогию:
 ,
, 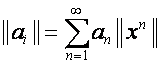 .
.
Так как
![]() ,
,
то
![]() ;
;
так
как
![]() ,
,
то
![]() .
.
Так
как
![]() ,
,
то
![]() является степенным
рядом:
является степенным
рядом:
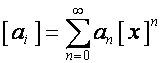 ;
;
так
как
![]() ,
,
то ![]() является суммой
является суммой ![]() и бесконечного множества степенных рядов вида
и бесконечного множества степенных рядов вида
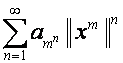 ,
,
где ![]() и не принимает
значений, равных степени натурального числа, отличной от
и не принимает
значений, равных степени натурального числа, отличной от ![]() .
.
Отсюда видно, что если при фиксированном ![]() из матрицы
из матрицы ![]() удалить все строки,
кроме строк с номерами
удалить все строки,
кроме строк с номерами ![]() и все столбцы, кроме столбцов с номерами
и все столбцы, кроме столбцов с номерами ![]() , то получится обычная матрица умножения. Например, при
, то получится обычная матрица умножения. Например, при ![]() ,
, ![]() :
:
 ,
,  .
.
Действительно,
матрицы вида
 ,
, ![]() ,
,
будучи степенными рядами, задают алгебру, изоморфную ![]() -алгебре: если
-алгебре: если
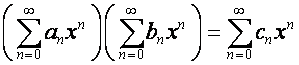 ,
,
то
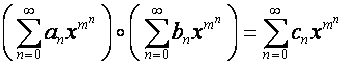 .
.
Например,
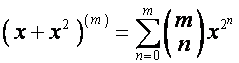 ,
,
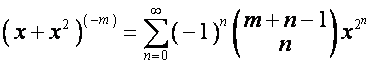 .
.
И
вообше, если
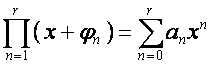 ,
,
то
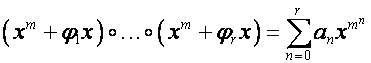 ,
, ![]() .
.
В ![]() -алгебре векторы вида
-алгебре векторы вида 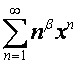 играют ту же роль, которую векторы вида
играют ту же роль, которую векторы вида 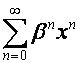 играют в
играют в ![]() -алгебре. Последняя обладает свойством, позволяющим свободно
манипулировать областью сходимости рядов. А именно, если
-алгебре. Последняя обладает свойством, позволяющим свободно
манипулировать областью сходимости рядов. А именно, если
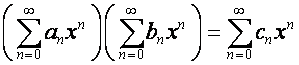 ,
,
то
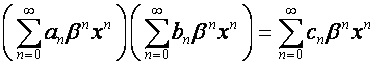 .
.
Это свойство обусловлено тем, что матрица ![]() как матрица степеней
отображает произведение векторов на произведение их образов:
как матрица степеней
отображает произведение векторов на произведение их образов:
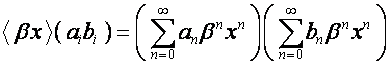 .
.
![]() -алгебра обладает аналогичным свойством: если
-алгебра обладает аналогичным свойством: если
 ,
,
то
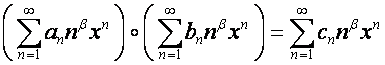 .
.
Обозначим
 .
.
Матрицу, ![]() -м столбцом которой является вектор
-м столбцом которой является вектор ![]() , обозначим
, обозначим ![]() . Например,
. Например,
 ,
,  .
.
Видно, что матрица ![]() не имеет обратной.
не имеет обратной.
Рассмотрим одностороннее произведение
матрицы ![]() с матрицей степеней
с матрицей степеней ![]() ,
, 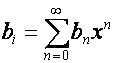 . Так как
. Так как
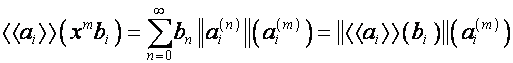 ,
,
то
![]() ,
,
или
![]() .
.
Таким образом, матрица ![]() отображает
отображает ![]() -произведение векторов на
-произведение векторов на ![]() -произведение их образов. Следовательно,
-произведение их образов. Следовательно,
![]() .
.
Отсюда получаем для ![]() -алгебры аналоги операций возведения в степень и
логарифмирования. Обозначим:
-алгебры аналоги операций возведения в степень и
логарифмирования. Обозначим:
![]() ,
, ![]() ,
,
так что
![]() ;
;
![]() ,
, ![]() .
.
Так
как
![]() ,
,
то
![]() .
.
Отсюда
вытекает, что
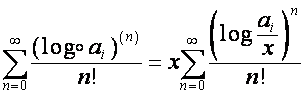 ,
,
где
 ;
;
![]() .
.
Так
как
 ,
,
то
![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() . Тогда
. Тогда
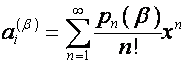 .
.
4
Представление числа ![]() в виде произведения
натуральных множителей, упорядоченных по возрастанию, будем называть
разложением числа
в виде произведения
натуральных множителей, упорядоченных по возрастанию, будем называть
разложением числа ![]() на множители. Пусть
на множители. Пусть
 ,
, 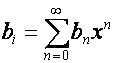 .
.
Выявим интересную аналогию между строками матриц ![]() и
и ![]() с одной стороны и
разбиениями на слагаемые и разложениями на множители числа
с одной стороны и
разбиениями на слагаемые и разложениями на множители числа ![]() – с другой.
– с другой.
Представим таблицу, строки которой
образуются последовательным умножение различных векторов:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , …
, …
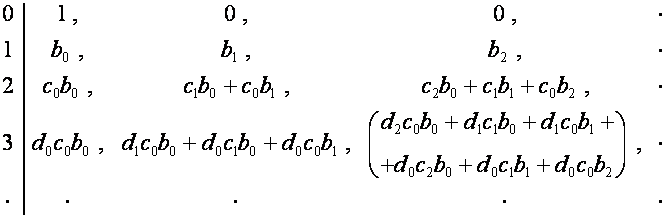
Алгоритм операции умножения приводит к тому, что
множеству слагаемых в разложении ![]() -го члена
-го члена ![]() -й строки таблицы соответствует множество размещений
-й строки таблицы соответствует множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() различным ячейкам:
различным векторам соответствуют различные ячейки, номеру члена соответствует
число предметов в ячейке.
различным ячейкам:
различным векторам соответствуют различные ячейки, номеру члена соответствует
число предметов в ячейке.
Если ![]() , таблица принимает
вид
, таблица принимает
вид
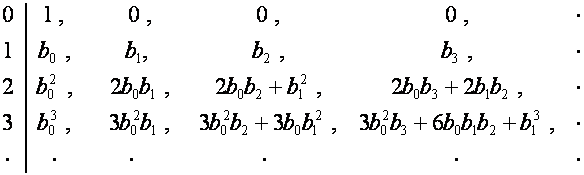
Множеству слагаемых в разложении ![]() -го члена
-го члена ![]() -й строки таблицы соответствует множество размещений
-й строки таблицы соответствует множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() неразличимым ячейкам:
выражение
неразличимым ячейкам:
выражение ![]() означает, что в
соответствующем слагаемому размещении
означает, что в
соответствующем слагаемому размещении ![]() ячеек содержат
одинаковое число предметов, равное
ячеек содержат
одинаковое число предметов, равное ![]() . Коэффициент при
. Коэффициент при ![]() равен
равен  .
.
Множество размещений ![]() неразличимых предметов
по
неразличимых предметов
по ![]() неразличимым ячейкам можно разбить на подмножества размещений
с одинаковым числом пустых ячеек, равным
неразличимым ячейкам можно разбить на подмножества размещений
с одинаковым числом пустых ячеек, равным ![]() . Каждому такому подмножеству соответствует множество
разбиений числа
. Каждому такому подмножеству соответствует множество
разбиений числа ![]() на
на ![]() слагаемых. При
слагаемых. При ![]() число подмножеств
равно
число подмножеств
равно ![]() , при
, при ![]() число подмножеств
равно
число подмножеств
равно ![]() .
.
Таким образом, ![]() -й столбец таблицы,
-й столбец таблицы, ![]() , можно представить в виде
, можно представить в виде

![]() ,
,
где
 ,
, ![]() ,
,
выражению  соответствует разбиение
соответствует разбиение 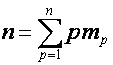 ,
,  и суммирование ведется
по всем разбиениям числа
и суммирование ведется
по всем разбиениям числа ![]() на
на ![]() слагаемых. Коэффициент при
слагаемых. Коэффициент при ![]() в
в ![]() -й строке таблицы равен вынесенному за знак суммы
произведению величины
-й строке таблицы равен вынесенному за знак суммы
произведению величины ![]() с ее долей
комбинаторного коэффициента, т.е.
с ее долей
комбинаторного коэффициента, т.е. 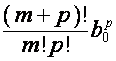 .
.
Матрицу, ![]() -й строкой которой является полином
-й строкой которой является полином
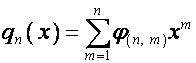 ,
, ![]() ,
,
обозначим
![]() . Тогда, как видно из таблицы,
. Тогда, как видно из таблицы,
![]() ,
,
и,
следовательно,
![]()
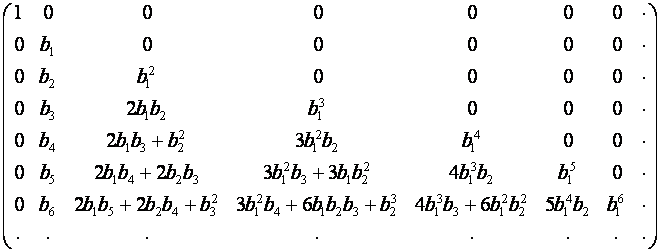
Отсюда, при ![]() , получаем выражение значений
, получаем выражение значений ![]() и
и ![]() через значения
через значения ![]() :
: ![]() -й член
-й член ![]() ,
, ![]() , равен
, равен
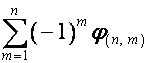 ,
,
![]() -й член
-й член ![]() равен
равен
 .
.
При ![]()
 ,
, ![]() ;
; 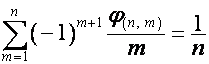 ,
,
где
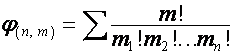 ,
, 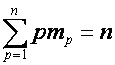 ,
, 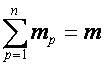 ,
,
и
суммирование ведется по всем разбиениям числа ![]() на
на ![]() слагаемых.
слагаемых.
Рассмотрим таблицу, ![]() -й строкой которой является
-й строкой которой является ![]() :
:
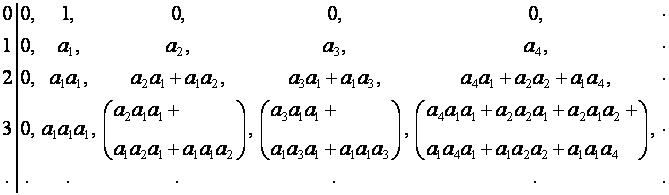
Представим
ее в виде:

Алгоритм операции ![]() -умножения приводит к тому, что множеству слагаемых в
разложении
-умножения приводит к тому, что множеству слагаемых в
разложении ![]() -го члена,
-го члена, ![]() ,
, ![]() -й строки таблицы соответствует множество разложений числа
-й строки таблицы соответствует множество разложений числа ![]() на
на ![]() множителей: выражению
множителей: выражению 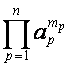 соответствует разложение
соответствует разложение  ,
,  ; коэффициент перед
; коэффициент перед ![]() равен
равен 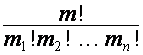 .
.
Множество разложений числа ![]() на
на ![]() множителей можно
разбить на подмножества разложений с одинаковым числом единичных множителей,
равным
множителей можно
разбить на подмножества разложений с одинаковым числом единичных множителей,
равным ![]() ; каждому такому подмножеству соответствует множество
разложений числа
; каждому такому подмножеству соответствует множество
разложений числа ![]() на
на ![]() неединичных
множителей. Число подмножеств не может быть больше числа множителей в
разложении
неединичных
множителей. Число подмножеств не может быть больше числа множителей в
разложении ![]() на простые множители.
на простые множители.
Таким образом, ![]() -й столбец таблицы,
-й столбец таблицы, ![]() , можно представить в виде
, можно представить в виде
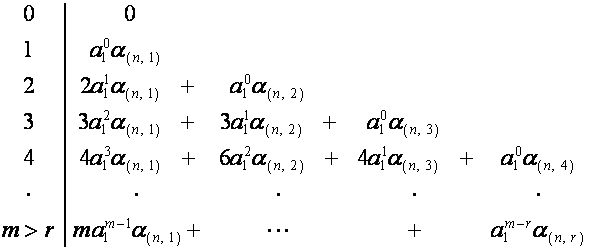 ,
,
где ![]() – число множителей в
разложении
– число множителей в
разложении ![]() на простые множители,
на простые множители,
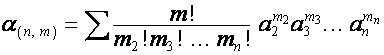 ,
, ![]() ,
,
выражению  соответствует разложение
соответствует разложение
 ,
, 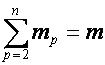 , и суммирование ведется по всем разложениям числа
, и суммирование ведется по всем разложениям числа ![]() на
на ![]() неединичных
множителей. Коэффициент перед
неединичных
множителей. Коэффициент перед ![]() в
в ![]() -й строке таблицы равен вынесенному за знак суммы произведению
величины
-й строке таблицы равен вынесенному за знак суммы произведению
величины ![]() с ее долей комбинаторного коэффициента, т.е.
с ее долей комбинаторного коэффициента, т.е. 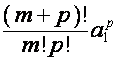 .
.
Матрицу, ![]() -й строкой которой является полином
-й строкой которой является полином
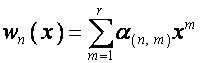 ,
, ![]() ,
, ![]() ,
,
обозначим ![]() . Тогда, как видно из таблицы,
. Тогда, как видно из таблицы,
![]()
и, следовательно,
![]() :
:
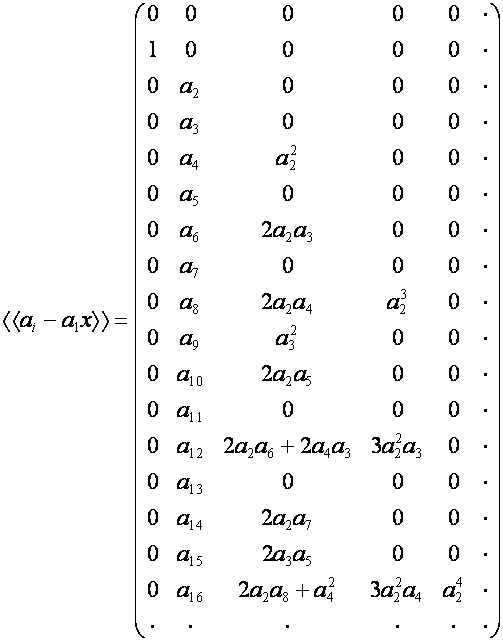
Отсюда при ![]() получаем выражение
значений
получаем выражение
значений ![]() и
и ![]() через значения
через значения ![]() :
: ![]() -й член
-й член ![]() ,
, ![]() , равен
, равен
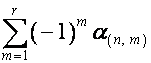 ,
,
где ![]() – число множителей в
разложении
– число множителей в
разложении ![]() на простые множители,
на простые множители, ![]() -й член
-й член ![]() равен
равен
 .
.
5
Рассмотрим фрагмент таблицы, ![]() -й строкой которой является
-й строкой которой является ![]() :
:
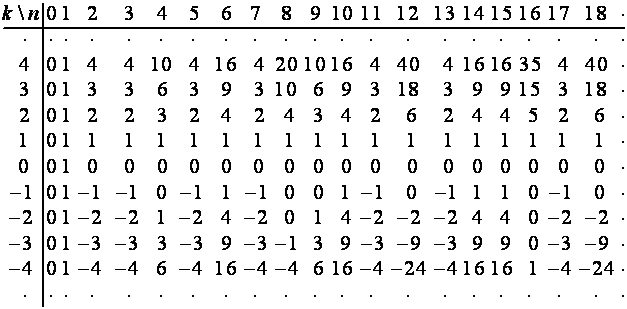
Пусть символ ![]() означает единицу.
Символ
означает единицу.
Символ ![]() ,
, ![]() , определим рекуррентной формулой
, определим рекуррентной формулой
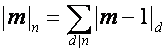 ,
,
так
что ![]() означает число
делителей числа
означает число
делителей числа ![]() , и т.д.:
, и т.д.:
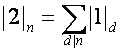 ,
, 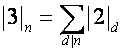 , …
, …
По определению ![]() -й член вектора
-й член вектора ![]() ,
, ![]() ,
, ![]() , равен
, равен ![]() .
.
Представим таблицу, ![]() -й строкой которой, является вектор
-й строкой которой, является вектор ![]() :
:

![]() -й член
-й член ![]() -й строки таблицы
– обозначим его
-й строки таблицы
– обозначим его ![]() – равен сумме
– равен сумме ![]() первых членов
предыдущей строки. Если
первых членов
предыдущей строки. Если ![]() – простое число, то,
как видно из таблицы,
– простое число, то,
как видно из таблицы,
![]() .
.
Пусть ![]() , где
, где ![]() ,
, ![]() – различные простые
числа,
– различные простые
числа, ![]() ,
, ![]() – натуральные числа.
Тогда
– натуральные числа.
Тогда
 .
.
Отсюда
выводим
 ,
,
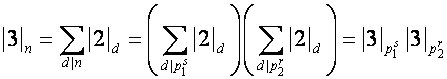 ,
,
![]() .
.
Обобщая,
выводим: если
![]() ,
,
то
![]() .
.
Так
как
 ,
,
то
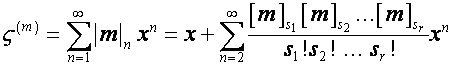 ,
,
где ![]() – возрастающий факториал длины
– возрастающий факториал длины ![]() ,
, ![]() – показатель степени
простого числа в каноническом разложении числа
– показатель степени
простого числа в каноническом разложении числа ![]() .
.
Матрицу, нулевая и первая строки которой
соответственно ![]() и
и ![]() , а
, а ![]() -я строка имеет вид
-я строка имеет вид
 ,
,
обозначим ![]() . Тогда
. Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, если ![]() –
– ![]() -я строка матрицы
-я строка матрицы
![]() ,
,
то
![]() ,
, ![]() ,
,  ,
,
где
![]() ,
,
![]() – показатель степени простого числа в каноническом разложении
числа
– показатель степени простого числа в каноническом разложении
числа ![]() ,
,
 .
.
Последовательность коэффициентов ряда ![]() , рассматриваемая как функция, заданная на множестве
натуральных чисел, называется функцией Мёбиуса, обозначается
, рассматриваемая как функция, заданная на множестве
натуральных чисел, называется функцией Мёбиуса, обозначается ![]() и определяется
следующим образом: если
и определяется
следующим образом: если
![]()
–
каноническое разложение числа ![]() , то
, то
![]() ,
,
![]() , если какое-либо
, если какое-либо ![]() ,
,
![]() , если все
, если все ![]() .
.
Это
соответствует нашему определению:
![]() при
при ![]() ,
,
![]() .
.
Обозначим:
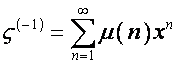 ,
, 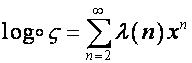 .
.
Согласно
результатам предыдущего раздела,
 ,
,  ,
, ![]() ,
,
где
![]() – число множителей в
разложении
– число множителей в
разложении ![]() на простые множители,
на простые множители,
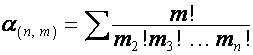 ,
,  ,
, 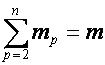 ,
,
и
суммирование ведется по всем разложениям числа ![]() на
на ![]() неединичных
множителей.
неединичных
множителей.
Из определения полинома  вытекает, что
вытекает, что ![]() , если
, если ![]() не является степенью
простого числа, так как в этом случае первый член полинома
не является степенью
простого числа, так как в этом случае первый член полинома  , т.е.
, т.е. ![]() -й строки матрицы
-й строки матрицы ![]() , равен нулю. Если
, равен нулю. Если ![]() , где
, где ![]() – простое число, то
первый член полинома
– простое число, то
первый член полинома  равен
равен  . Так как первый столбец матрицы
. Так как первый столбец матрицы ![]() совпадает с первым
столбцом матрицы
совпадает с первым
столбцом матрицы ![]() , то
, то ![]() , если
, если ![]() .
.
6
Обозначим
![]() ,
,
где
![]() . Свойство логарифма
. Свойство логарифма
![]()
подсказывает, что ![]() -алгебру можно рассматривать как алгебру логарифмов,
представляя векторы
-алгебру можно рассматривать как алгебру логарифмов,
представляя векторы ![]() ,
, ![]() в виде
в виде
![]() ,
, ![]() .
.
Тогда
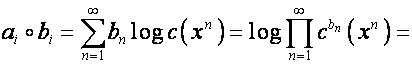
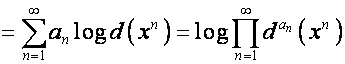 .
.
Если
при этом ![]() , то
, то
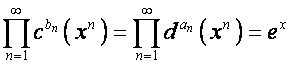 .
.
![]() -й член вектора
-й член вектора ![]() обозначим
обозначим ![]() . Тогда по формуле Файна [4. стр.180], учитывая, что
. Тогда по формуле Файна [4. стр.180], учитывая, что ![]() ,
,
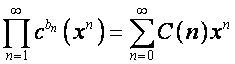 ,
,
где
![]() ,
, 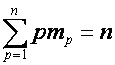 ,
,
и
суммирование ведется по всем разбиениям числа ![]() .
.
Литература:
1. Пойа Д. Математика и правдоподобные
рассуждения. М.: Наука, 1975.
2. Риордан Д. Введение в комбинаторный
анализ. М.: ИЛ, 1963.
3. Сачков В.
Н. Комбинаторные методы дискретной математики. М.: Наука, 1977.
4. Риордан Д.
Комбинаторные тождества. М.: Наука, 1982.