Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
(Продолжение; начало см. в [1])
6.
«Металлические пропорции»
6.1
«Металлической пропорцией» (в честь «золотой
пропорции») [2] называется положительный корень уравнения ![]() :
:
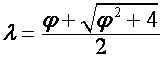 ,
, ![]() .
.
Отсюда видно, что если ![]() , то
, то ![]() . Следовательно,
. Следовательно,
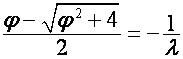 .
.
«Золотая
пропорция»
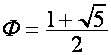
характеризуется следующими
свойствами:
![]() ,
,
где ![]() – целое число,
– целое число,
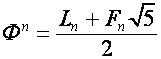 ,
, 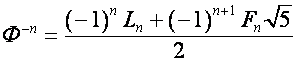 ,
,
где
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Так как производящие функции чисел ![]() (числа Люка) и
(числа Люка) и ![]() (числа Фибоначчи)
имеют вид
(числа Фибоначчи)
имеют вид
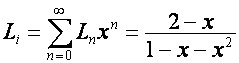 ,
, 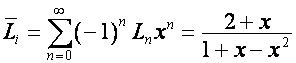 ,
,
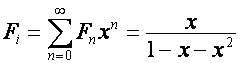 ,
, 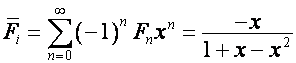 ,
,
то
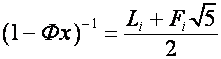 ,
, 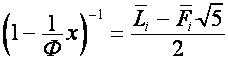 ,
,
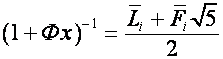 ,
, 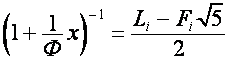 .
.
Любое положительное число является «металлической пропорцией»,
т.е. значением функции ![]() . Перечисленные свойства «золотой пропорции» являются
функциональными свойствами «металлической пропорции» и зависят от параметра
. Перечисленные свойства «золотой пропорции» являются
функциональными свойствами «металлической пропорции» и зависят от параметра ![]() , который при
, который при ![]() равен единице.
равен единице.
Так как формула «металлической пропорции» является
частным случаем формулы корня квадратного уравнения, она указывает на
определенную связь квадратных уравнений с гиперболическими функциями.
Покажем, что проблематика «металлических пропорций»
неразрывно связана с обобщенным преобразованием
Эйлера.
Рассмотрим преобразования
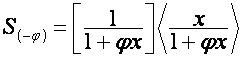 ,
,
 .
.
Для вектора 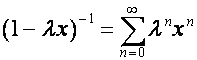 имеем
имеем
![]() ,
,
![]() .
.
Если
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
где
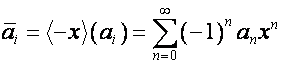 .
.
Составляющие произвольного вектора ![]() в пространствах
в пространствах ![]() и
и ![]() соответственно равны
соответственно равны
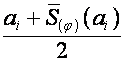 ,
, 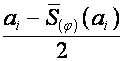 ,
,
так
что
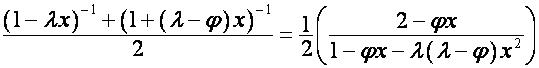 ,
,
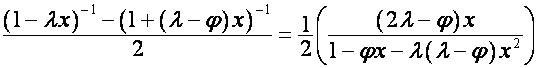 .
.
Рассмотрим вектор
![]() ,
, ![]() , обладающий свойством
, обладающий свойством
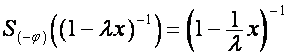 .
.
Его
составляющие в пространствах ![]() и
и ![]() обозначим соответственно
обозначим соответственно
![]() и
и 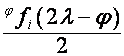 . Так как
. Так как
![]() ,
, 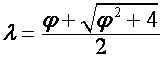 ,
,
то
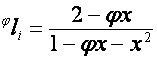 ,
, 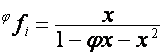 ,
,
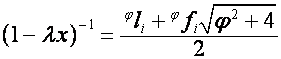 ,
,
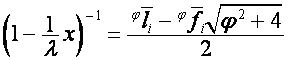 ,
,
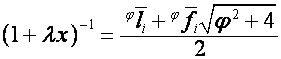 ,
,
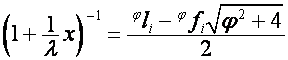 .
.
Числу
![]() поставим в
соответствие ряд
поставим в
соответствие ряд ![]() ,
,
![]() ,
,
![]() ,
,
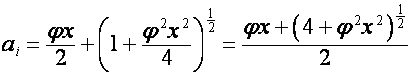 ,
,
по правилу:
![]() ,
,
где ![]() – аналитическая запись
ряда
– аналитическая запись
ряда ![]() . Тогда
. Тогда
![]() ,
,
где ![]() – аналитическая запись
ряда
– аналитическая запись
ряда ![]() . В разделе 5.3 мы выяснили, что
. В разделе 5.3 мы выяснили, что
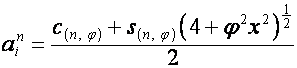 ,
,
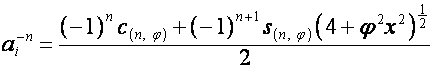 ,
,
где
![]() :
:
![]() ,
, 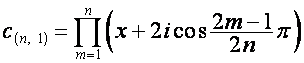 ;
;
![]() :
:
![]() ,
, ![]() ,
, 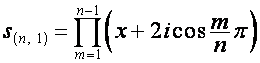 .
.
Отсюда видно, что
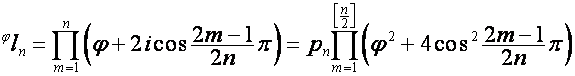 ,
,
![]() ,
, ![]() ,
,
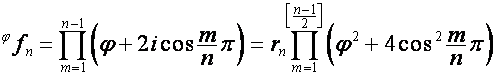 ,
,
![]() ,
, ![]() .
.
Пусть
![]() ,
, ![]() . Тогда
. Тогда
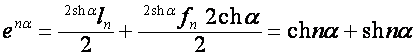 ,
,
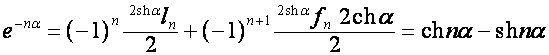 .
.
Следовательно,
![]() ,
, ![]() ,
,
![]() ,
, 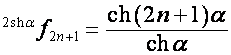 ,
,
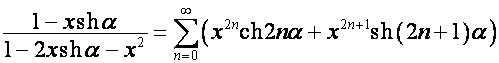 ,
,
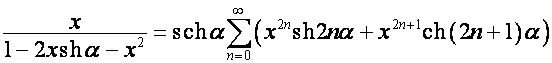 .
.
6.2
Рассмотрим аналогичный случай. Чтобы не усложнять
символику и подчеркнуть аналогию, будем пользоваться обозначениями из
предыдущего раздела.
Рассмотрим вектор ![]() ,
, ![]() , обладающий свойством
, обладающий свойством
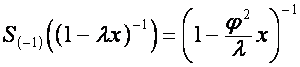 .
.
Его
составляющие в пространствах ![]() и
и ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и 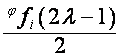 . Так как
. Так как
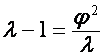 ,
, 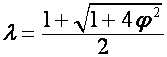 ,
,
то
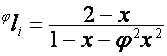 ,
, 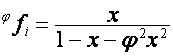 ,
,
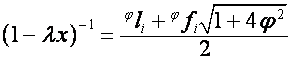 ,
,
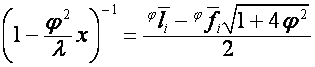 ,
,
 ,
,
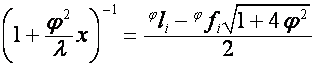 .
.
Числу
![]() поставим в
соответствие ряд
поставим в
соответствие ряд ![]() ,
,
![]() ,
,
![]() ,
,
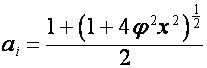 .
.
Раскладывая ![]() в бином Ньютона и группируя
члены, можно представить его в виде
в бином Ньютона и группируя
члены, можно представить его в виде
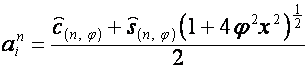 ,
,
где
![]() – полином степени
– полином степени ![]() ,
, ![]() – полином степени
– полином степени ![]() . Сравнивая алгоритм получения полиномов
. Сравнивая алгоритм получения полиномов ![]() и
и ![]() с алгоритмом получения
полиномов
с алгоритмом получения
полиномов ![]() и
и ![]() при разложении в бином
Ньютона
при разложении в бином
Ньютона
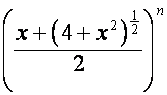 ,
,
заключаем,
что ![]() и
и ![]() получаются из
получаются из ![]() и
и ![]() перестановкой
коэффициентов в обратном порядке и понижением степени на единицу для
перестановкой
коэффициентов в обратном порядке и понижением степени на единицу для ![]() и
и ![]() . Например:
. Например:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Таким образом,
![]() ,
, ![]() ,
,
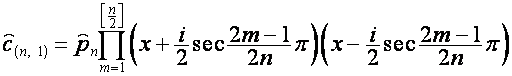 ,
,
где
![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
,
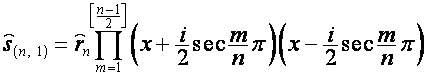 ,
,
где
![]() ,
, ![]() .
.
В
разделе 5.2 мы получили этот же результат, сопоставляя корни полиномов ![]() и
и ![]() с корнями полиномов
с корнями полиномов ![]() и
и ![]() .
.
Так
как
![]() ,
,
или
 ,
,
то
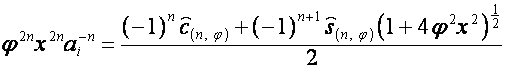 .
.
Отсюда видно, что
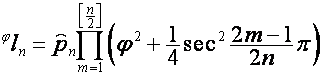 ,
,
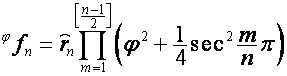 .
.
Так
как при ![]()
 ,
,
то пусть
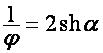 ,
, ![]() .
.
Тогда
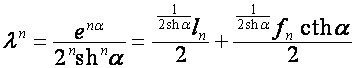 ,
,
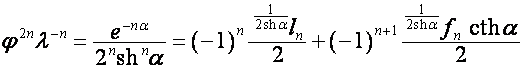 .
.
Но
нет необходимости искать выражение чисел ![]() ,
, ![]() таким образом. Так как
таким образом. Так как
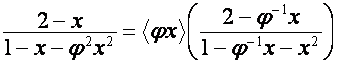 ,
,
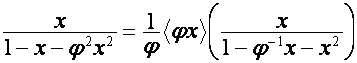 ,
,
то
числа ![]() ,
, ![]() из настоящего раздела
отличаются от чисел
из настоящего раздела
отличаются от чисел ![]() ,
, ![]() из предыдущего раздела
множителями
из предыдущего раздела
множителями ![]() ,
, ![]() соответственно.
Например,
соответственно.
Например,
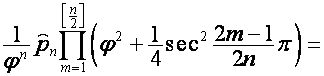
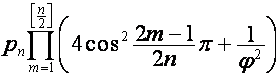 ,
,
где
![]() ,
, 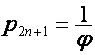 , так как множитель
, так как множитель 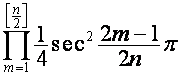 равен
равен ![]() , если
, если ![]() четно, и
четно, и ![]() , если
, если ![]() нечетно.
нечетно.
Аналогично,
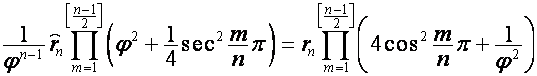 ,
,
где
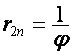 ,
, ![]() , так как множитель
, так как множитель 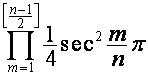 равен
равен ![]() , если
, если ![]() четно, и
четно, и ![]() , если
, если ![]() нечетно.
нечетно.
6.3
Для полноты картины рассмотрим еще один аналогичный случай.
Ради удобства записи введем нормирующий множитель ![]() , тем самым немного нарушив аналогию.
, тем самым немного нарушив аналогию.
Пусть
вектор ![]() ,
, ![]() , обладает свойством
, обладает свойством
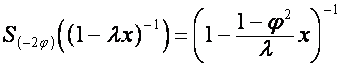 ,
,
Его
составляющие в пространствах ![]() и
и ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и ![]() . Так как
. Так как
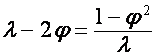 ,
, ![]() ,
,
то
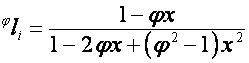 ,
, 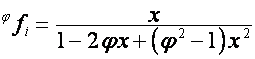 ,
,
![]() ,
, 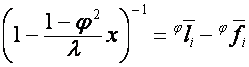 ,
,
![]() ,
, 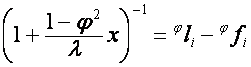 .
.
Числу
![]() поставим в
соответствие ряд
поставим в
соответствие ряд ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
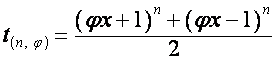 ,
, 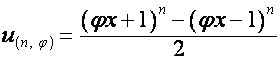 .
.
Так
как
![]() ,
, 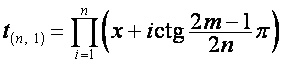 ,
,
![]() ,
, ![]() ,
, 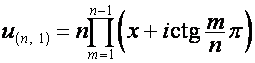 ,
,
то
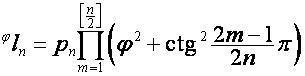 ,
, ![]() ,
, ![]() ,
,
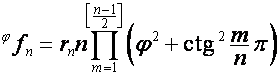 ,
, ![]() ,
, ![]() .
.
Так
как при ![]()
 ,
,
то пусть
 ,
, ![]() .
.
Тогда
 ,
,
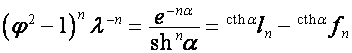 ,
,
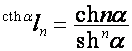 ,
, 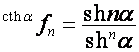 ,
,
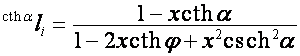 ,
, 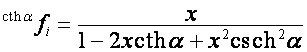 ,
,
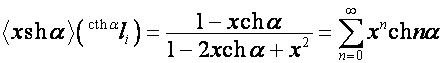 ,
,
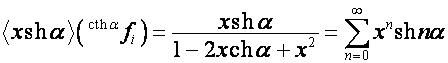 .
.
Так как
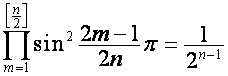 ,
, 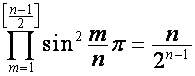 ,
,
то
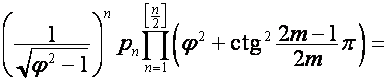
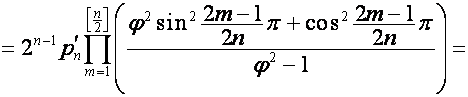
 ,
, ![]() ,
, 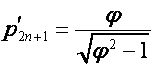 ,
,
или
 ;
;
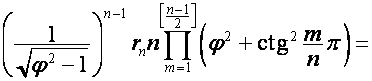
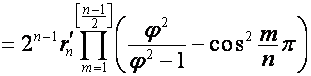 ,
,  ,
, ![]() ,
,
или
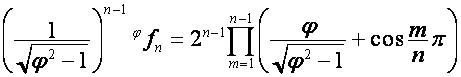 .
.
Так как при ![]()
 ,
,
то пусть
 ,
, ![]() .
.
Тогда
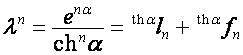 ,
,
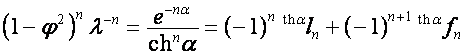 ,
,
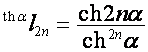 ,
, 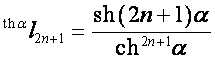 ,
,
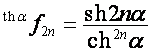 ,
, 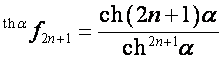 ;
;
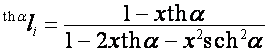 ,
, 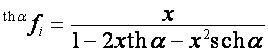 ,
,
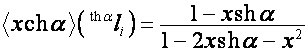 ,
,
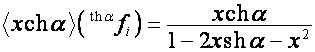 ;
;
 ,
,
 .
.
6.4
Из
рассмотренных примеров выделим суть.
В разделе 4.1, посвященном собственным базисам
преобразования ![]() , мы выяснили, что если
, мы выяснили, что если
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() .
.
Пусть
![]() .
.
Тогда
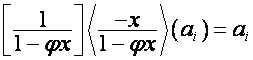 ,
,
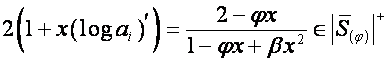 ,
, 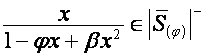 .
.
Обозначим:
![]() ,
, 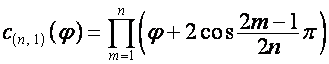 ,
,
![]() ,
, ![]() ,
, 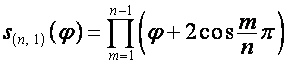 .
.
Тогда
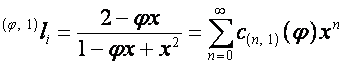 ,
,
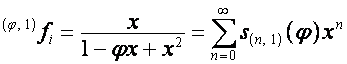 .
.
Так
как при ![]() (напомним, что присутствие мнимой единицы
мы допускаем только в корнях
полиномов)
(напомним, что присутствие мнимой единицы
мы допускаем только в корнях
полиномов)
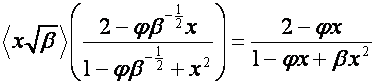 ,
,
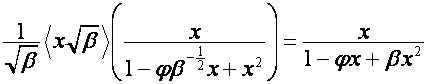 ,
,
то
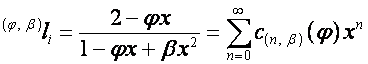 ,
,
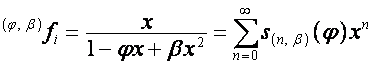 ,
,
где
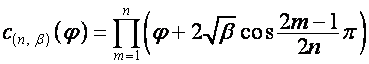 ,
,
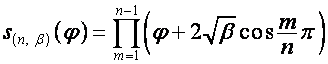 .
.
Таким образом,
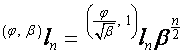 ,
, 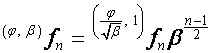 ,
,
или
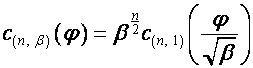 ,
, 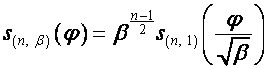 .
.
Тогда,
учитывая, что ![]() ,
, ![]() , совпадают с
полиномами Чебышева
, совпадают с
полиномами Чебышева ![]() ,
, ![]() (см. раздел 5.2),
(см. раздел 5.2),
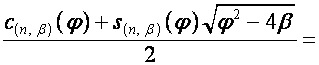

 ;
;

 .
.
Таким образом, 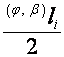 и
и 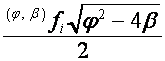 ,
, ![]() , являются соответственно
, являются соответственно ![]() – составляющей и
– составляющей и ![]() – составляющей вектора
– составляющей вектора ![]() .
.
Воспользуемся мнимой единицей для вспомогательных вычислений.
Если 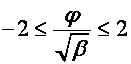 , то пусть
, то пусть 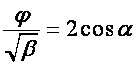 ,
, 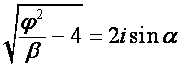 . Тогда
. Тогда
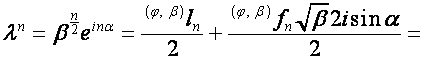
![]() ,
,
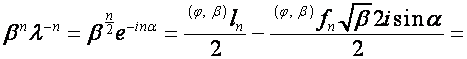
![]() ,
,
![]() ,
, 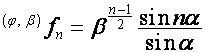 .
.
Если 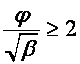 , то пусть
, то пусть 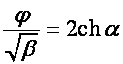 ,
, 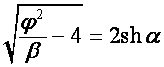 . Тогда
. Тогда
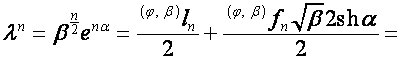
![]() ,
,
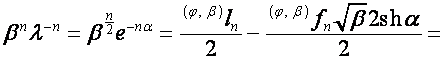
![]() ,
,
![]() ,
, 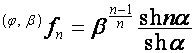 .
.
Если
![]() , или
, или ![]() , формула
, формула ![]() остается применимой:
остается применимой:
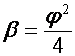 ,
, 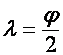 ,
, ![]() ;
;
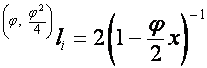 ,
, 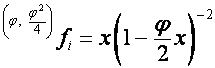 ;
;
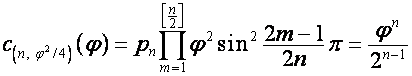 ,
,
![]() ,
, ![]() ;
;
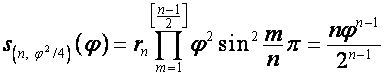 ,
,
![]() ,
, ![]() .
.
Пусть
по-прежнему ![]() . Обозначим:
. Обозначим:
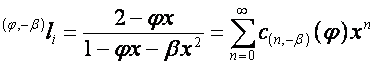 ,
,
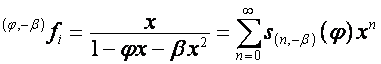 ,
,
где
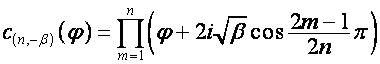 ,
,
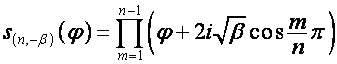 .
.
Тогда
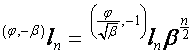 ,
, 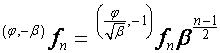 ,
,
или
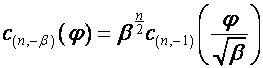 ,
, 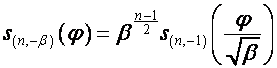 ;
;
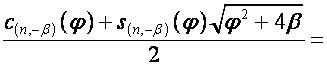

 ;
;

 .
.
Пусть
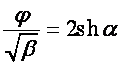 ,
, 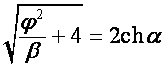 . Тогда
. Тогда
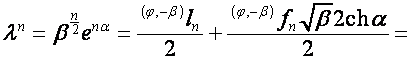
![]() ,
,
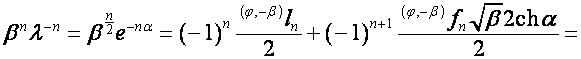
![]() ,
,
![]() ,
, ![]() ,
,
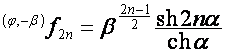 ,
, 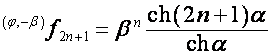 .
.
Например,
при ![]() ,
, ![]() ,
, ![]() :
:
 ,
,  ,
,
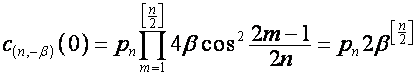 ,
,
![]() ,
, ![]() ;
;
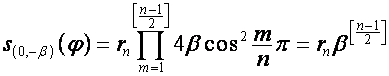 ,
,
![]() ,
, ![]() .
.
Отдельно
выделим случай:
![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ;
;
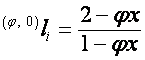 ,
, 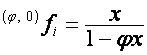 ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
В заключение предупредим одно возможное замечание.
Может показаться, что наши подробные
выкладки сводятся к элементарным
равенствам:
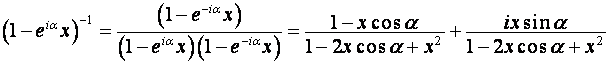 ,
,
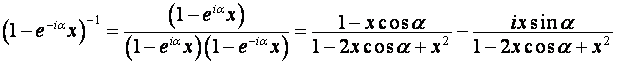 ;
;
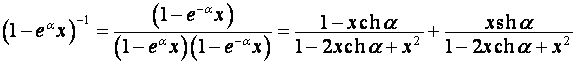 ,
,
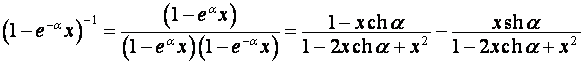 ;
;
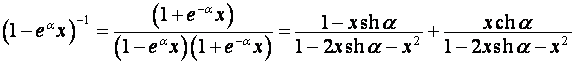 ,
,
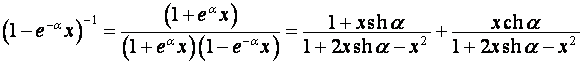 ,
,
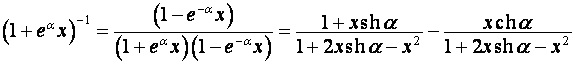 ,
,
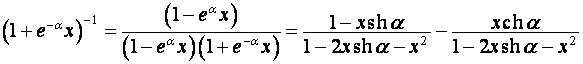 .
.
Но
нашей целью является не получение равенств, а изучение алгебраического
механизма, взаимодействие частей которого
эти равенства обеспечивают. Что касается перечисленных равенств, то мы определили их основное место
работы – механизм обобщенного преобразования Эйлера.
Отметим, что так как матрица преобразования ![]() является
трансформацией матрицы
является
трансформацией матрицы ![]() :
:
![]() ,
,
то
операция
![]()
является
трансформацией операции
![]() .
.
Но
не следует придавать этому факту решающего значения. В данном случае
трансформация вызывает синергетический
эффект – будучи произведением матрицы умножения и матрицы степеней, а
также транспонированной матрицей степеней, матрица ![]() обладает свойствами,
аналоги которых у матрицы
обладает свойствами,
аналоги которых у матрицы ![]() отсутствуют.
отсутствуют.
Отметим также, что благодаря преобразованию «поворот»,
частным случаем которого является и обобщенное преобразование Эйлера, корень
уравнения ![]() ,
,
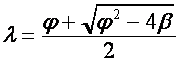 ,
,
воплощается в ряды
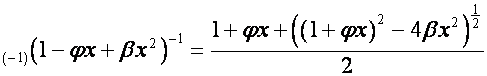 ,
,
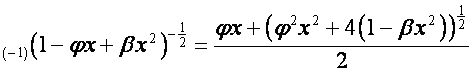 .
.
Как мы выяснили, этот факт
имеет прямое отношение к рассмотренной конструкции.
1.
Е. В. Бурлаченко. Алгебраические заметки.
2.
Стахов А. П . Металлические Пропорции – новые математические константы Природы.
www.trinitas.ru/rus/doc/0232/004a/02321079.htm
.