Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
(Продолжение; начало см. в [1])
4.3. Трансформации
4.3.1
Единичную матрицу
размерности ![]() обозначим
обозначим ![]() . Матрицу, которая получается из
. Матрицу, которая получается из ![]() перестановкой столбцов
в обратном порядке обозначим
перестановкой столбцов
в обратном порядке обозначим ![]() . Например,
. Например,
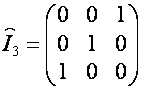 .
.
Матрица ![]() состоит из
состоит из ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() ; матрица
; матрица ![]() состоит из
состоит из ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() , переставленных в обратном порядке; матрица
, переставленных в обратном порядке; матрица ![]() состоит из
состоит из ![]() первых строк матрицы
первых строк матрицы ![]() , переставленных в обратном порядке.
, переставленных в обратном порядке.
Обозначим:
![]() .
.
Например:
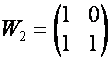 ,
, 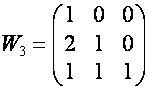 ,
,  .
.
![]() -м столбцом матрицы
-м столбцом матрицы ![]() является
является ![]() ,
, ![]() .
.
![]() .
.
Например:
 ,
,  ,
,  .
.
![]() -м столбцом матрицы
-м столбцом матрицы ![]() является
является ![]() ,
, ![]() .
.
Изучая преобразование
«поворот», мы выяснили, что
![]() ,
,
![]() .
.
Рассмотрим таблицы
![]()
![]()
 :
:
 :
:
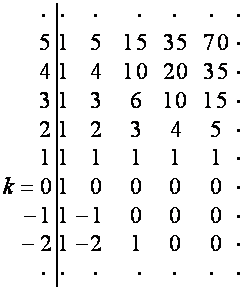 ,
,  ;
;
![]()
![]()
 :
: 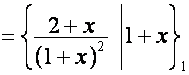 :
:
 ,
, 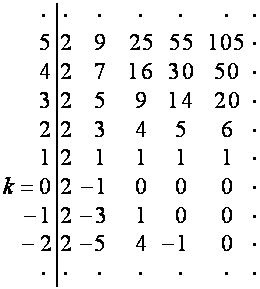 .
.
![]() -й столбец верхней половины таблицы
-й столбец верхней половины таблицы ![]() совпадает с
совпадает с ![]() -й строкой;
-й строкой; ![]() -й столбец верхней половины таблицы
-й столбец верхней половины таблицы ![]() ,
, ![]() , совпадает с
, совпадает с ![]() -й строкой, умноженной на
-й строкой, умноженной на ![]() ;
; ![]() -й столбец верхней половины таблицы
-й столбец верхней половины таблицы ![]() ,
, ![]() , совпадает с
, совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() .
.
Отметим,что
![]() ,
,
![]() ,
,
![]() .
.
Пусть ![]() – полином степени
– полином степени ![]() . Тогда:
. Тогда:
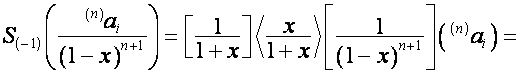
![]() ,
,
так как ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() совпадают со столбцами
матрицы
совпадают со столбцами
матрицы ![]() . Например,
. Например,
 ;
;
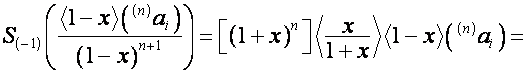
![]() ,
,
так как ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() совпадают со столбцами
матрицы
совпадают со столбцами
матрицы ![]() . Например,
. Например,
 .
.
Таким образом, если
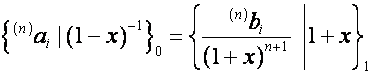 ,
,
то
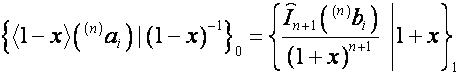 .
.
Так как
![]() ,
,
то
![]() .
.
Таким
образом, ![]() -й столбец верхней половины таблицы
-й столбец верхней половины таблицы ![]() ,
, ![]() , совпадает с
, совпадает с ![]() -й строкой таблицы
-й строкой таблицы ![]() , или
, или ![]() -й член вектора
-й член вектора  ,
, ![]() , равен
, равен ![]() -му члену вектора
-му члену вектора  , и наоборот:
, и наоборот: ![]() -й член вектора
-й член вектора 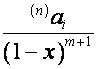 ,
, ![]() , равен
, равен ![]() -му члену вектора
-му члену вектора  .
.
4.3.2
Последовательности
столбцов матриц ![]() и
и ![]() ,
, ![]() ,
, ![]() , совпадают с последовательностями строк верхней и нижней
половин таблицы
, совпадают с последовательностями строк верхней и нижней
половин таблицы ![]() . Формулы
. Формулы
![]() ,
,
![]() ,
,
позволяют изучать
таблицу ![]() , рассматривая в качестве ее элементов не строки, а столбцы.
, рассматривая в качестве ее элементов не строки, а столбцы.
![]() -ю строку матрицы
-ю строку матрицы ![]() ,
, ![]() , обозначим
, обозначим
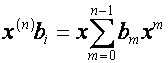 ,
,
так что ![]() – полином степени
– полином степени ![]() . Тогда
. Тогда ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид
![]()

 ,
,
где
![]() ,
,
так как ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() совпадают со столбцами
матрицы
совпадают со столбцами
матрицы ![]() . Например,
. Например,
 .
.
Так как
 ,
,
то ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , имеет вид
, имеет вид
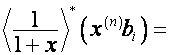
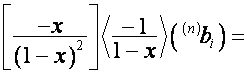
 ,
,
где
![]() ,
,
так как ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() совпадают со столбцами
матрицы
совпадают со столбцами
матрицы ![]() . Например,
. Например,
 ,
,
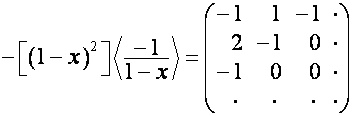 .
.
Таким
образом, ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , имеет вид
, имеет вид 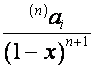 , где
, где ![]() – полином степени
– полином степени ![]() ;
; ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , имеет вид
, имеет вид  , где
, где ![]() – полином степени
– полином степени ![]() ; и, что самое интересное,
; и, что самое интересное,
![]() .
.
Например, если ![]() , то
, то ![]() ,
, ![]() ,
, ![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() , где
, где ![]() , обозначим
, обозначим 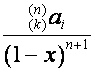 ,
, ![]() . Найдем преобразование
. Найдем преобразование
![]() , такое, что
, такое, что
![]() .
.
Диагональную
матрицу, диагональные элементы которой равны значениям вектора ![]() обозначим
обозначим ![]() :
:
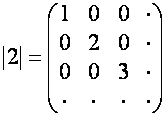 ,
, 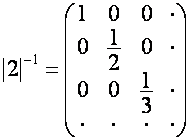 ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Мы знаем, что элементы
матриц ![]() и
и ![]() связаны равенством
связаны равенством
![]() ,
, ![]() ,
,
где верхний индекс –
номер столбца, нижний индекс – номер строки. Следовательно, если ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид  , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид  .
.
Преобразование
![]() отображает
отображает ![]() на
на 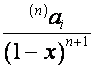 ; преобразование
; преобразование ![]() ,
,

 ,
,
отображает 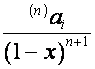 на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() , т.е. на
, т.е. на  . Таким образом,
. Таким образом,
![]() ,
,
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Применительно к ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Так как
![]() ,
,
то
![]() .
.
Окончательно получаем:
![]()
![]() ,
,
так как ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() совпадают со столбцами
матрицы
совпадают со столбцами
матрицы ![]() . Например,
. Например,

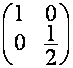
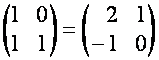 ,
,

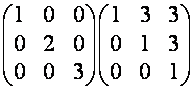

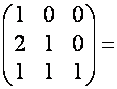
 ,
,
![]()

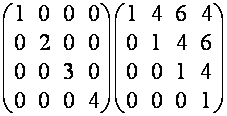


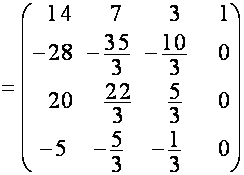 .
.
Пусть ![]() . Тогда
. Тогда ![]() . Так как
. Так как ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 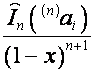 ,
, ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 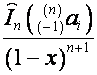 , то
, то
![]() ,
,
![]() .
.
Т.е. преобразование ![]() является отражением,
и
является отражением,
и
![]() .
.
Таким образом, ![]() получается из
получается из ![]() перестановкой в
обратном порядке строк и столбцов:
перестановкой в
обратном порядке строк и столбцов:
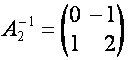 ,
, 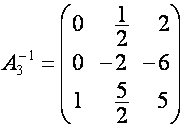 ,
,  .
.
Так как ![]() – определенная
модификация невырожденной матрицы умножения, естественным образом определяется
ее степень:
– определенная
модификация невырожденной матрицы умножения, естественным образом определяется
ее степень:
![]() .
.
Например,
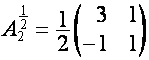 ,
, 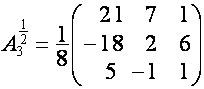 ,
,
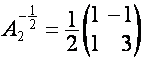 ,
, 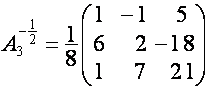
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() . Тогда
. Тогда
![]() ,
,
![]() ,
,
![]() .
.
4.3.3
Структура
преобразования ![]() станет более
прозрачной, если воспользоваться биномиальной формой записи.
станет более
прозрачной, если воспользоваться биномиальной формой записи.
Для формулы общего члена
последовательности введем обозначение
![]() ,
, ![]()
Если 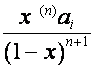 –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() ,
, 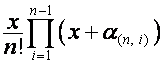 –
– ![]() -я строка матрицы
-я строка матрицы ![]() ,
, ![]() , то
, то
 ,
,
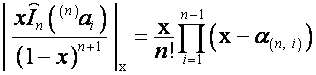 .
.
Рассмотрим выражение
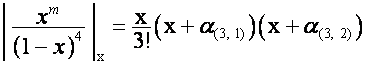 ,
, ![]()
Так как
![]() ,
, ![]() ,
, ![]() ,
,
то
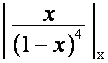 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
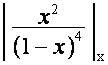 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
 должно равняться нулю
при подстановках
должно равняться нулю
при подстановках ![]()
Следовательно,
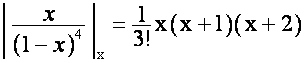 ,
,
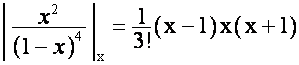 ,
,
 .
.
Обобщая, выводим:
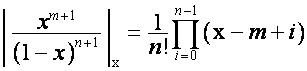 ,
, ![]() .
.
Матрицу, ![]() -м столбцом которой является полином
-м столбцом которой является полином
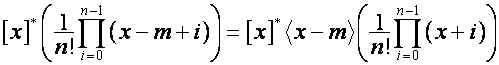 ,
,
![]() , обозначим
, обозначим ![]() . Например:
. Например:
 ,
, 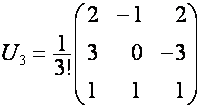 ,
,  .
.
(В
разделе 1.5, посвященном биномиальным последовательностям, символ ![]() означает
означает ![]() из настоящего раздела;
понятия биномиальной последовательности и биномиальной формы записи почти совпадают,
но для наших целей биномиальная форма записи более удобна.)
из настоящего раздела;
понятия биномиальной последовательности и биномиальной формы записи почти совпадают,
но для наших целей биномиальная форма записи более удобна.)
По определению
преобразования ![]() , если
, если
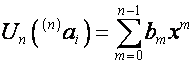 ,
,
то
 ,
,
так как
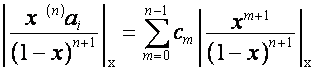 ,
,
где
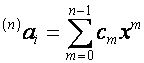 .
.
Таким
образом, преобразование ![]() отображает
отображает ![]() на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() , умноженную на
, умноженную на ![]() . Так как
. Так как
 ,
,
то
![]() ,
,
![]() .
.
Если ![]() , то
, то ![]() . Так как
. Так как ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид  , то
, то
![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() ,
, ![]() , в порядке исключения выделив множитель, обозначим
, в порядке исключения выделив множитель, обозначим 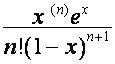 , где
, где ![]() совпадает с полиномом
Эйлера
совпадает с полиномом
Эйлера ![]() [1, с.254], [2, c.139]:
[1, с.254], [2, c.139]:
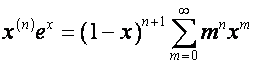
![]() ,
, ![]() ,
, ![]() ,
,
![]() , …
, …
Так как
 ,
,
то
![]() ,
, ![]() .
.
Таким
образом, ![]() -м столбцом матрицы
-м столбцом матрицы ![]() является вектор
является вектор ![]() :
:
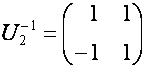 ,
, 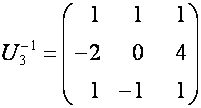 ,
,  .
.
Мы знаем,
что если ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид  , где
, где ![]() , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() имеет вид
имеет вид 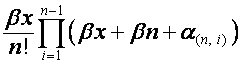 . Окончательно получаем:
. Окончательно получаем:
![]() .
.
Таким образом, равенство
![]() вытекает также из
равенств:
вытекает также из
равенств:
![]() ,
,
![]() ,
,
Обозначим:
![]() ,
,
![]() .
.
Так как
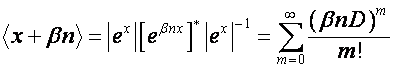 ,
,
то
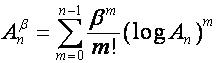 .
.
Например:
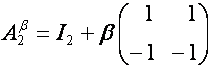 ,
,
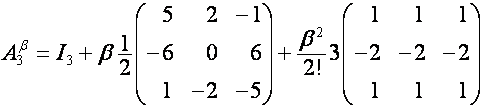 ,
,

 .
.
Так как
каждый столбец матрицы ![]() , кроме последнего, содержит множитель
, кроме последнего, содержит множитель ![]() , то каждый столбец матрицы
, то каждый столбец матрицы
![]() ,
, ![]() , также содержит множитель
, также содержит множитель ![]() и сумма его членов
равна нулю. Следовательно, сумма членов каждого столбца матрицы
и сумма его членов
равна нулю. Следовательно, сумма членов каждого столбца матрицы ![]() равна единице.
равна единице.
Таким
образом, преобразование ![]() сохраняет сумму
значений вектора.
сохраняет сумму
значений вектора.
![]() -ю строку матрицы
-ю строку матрицы 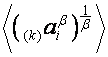 ,
, ![]() , обозначим
, обозначим  . Тогда
. Тогда![]()
![]()
![]() .
.
Так как
![]() ,
,
![]() ,
,
то
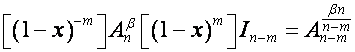 .
.
4.3.4
Обозначим:
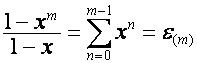 .
.
Диагональную матрицу,
диагональные элементы которой равны значениям вектора ![]() , обозначим
, обозначим ![]() :
:
 .
.
Вектор  раскладывается на
составляющие по правилу
раскладывается на
составляющие по правилу
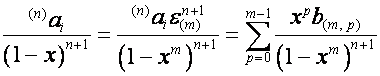 ,
,
где
![]() ,
,
 .
.
Например,
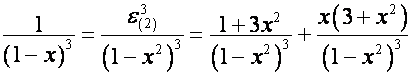 .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим 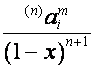 . Так как
. Так как ![]() -й член вектора
-й член вектора 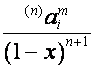 равен
равен ![]() -му члену вектора
-му члену вектора  , т.е.
, т.е.
 ,
,
где
 ,
,
то
![]() ,
,
где
 .
.
Обозначим:
![]() .
.
Например,
 .
.
Убедимся, что ![]() – квадратная матрица
размерности
– квадратная матрица
размерности ![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, 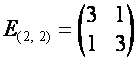 ,
,  .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, 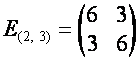 ,
, 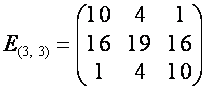 .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
, 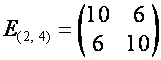 ,
, 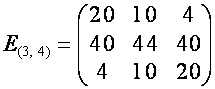 .
.
![]() ,
,
![]() .
.
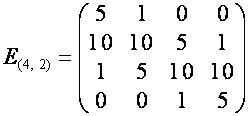 ,
,  .
.
Матрицу ![]() можно также представить следующим образом. Матрицу,
можно также представить следующим образом. Матрицу, ![]() -я строка которой совпадает с
-я строка которой совпадает с ![]() -й строкой матрицы
-й строкой матрицы ![]() , обозначим
, обозначим ![]() . Например:
. Например:
 ,
,  .
.
Матрица ![]() образована
пересечением
образована
пересечением ![]() первых строк и
первых строк и ![]() первых столбцов
матрицы
первых столбцов
матрицы ![]() при подстановке
при подстановке ![]() .
.
Преобразование ![]() отображает
отображает ![]() на
на ![]() . Отсюда вытекает, что, во-первых,
. Отсюда вытекает, что, во-первых,
![]() ,
,
во-вторых,
![]() ,
,
так как преобразование ![]() отображает
отображает ![]() -ю строку матрицы
-ю строку матрицы ![]() на
на ![]() -ю строку матрицы
-ю строку матрицы ![]() .
.
Таким
образом, ![]() является собственным
вектором преобразования
является собственным
вектором преобразования ![]() с собственным
значением
с собственным
значением ![]() .
.
Рассмотрим
равенство
![]() .
.
Каждый член вектора ![]() , начиная с
, начиная с ![]() -го, равен сумме членов вектора
-го, равен сумме членов вектора ![]() , т.е.
, т.е. ![]() . Следовательно, сумма членов вектора
. Следовательно, сумма членов вектора ![]() ,
, ![]() , также равна
, также равна ![]() .
.
Таким
образом, сумма членов каждого столбца матрицы
![]() равна
равна ![]() и на эту величину
преобразование
и на эту величину
преобразование ![]() умножает сумму
значений вектора.
умножает сумму
значений вектора.
Отметим
также, что
![]() ,
,
![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() . Так как
. Так как
![]() ,
,
то
![]()
![]()
![]() ;
;
![]() .
.
![]() -ю строку матрицы
-ю строку матрицы ![]() обозначим
обозначим ![]() , так что
, так что
![]() .
.
Если ![]() , то
, то ![]() -я строка матрицы
-я строка матрицы ![]() совпадает с
совпадает с ![]() . Так как
. Так как
![]() :
:



 ,
,
то
![]() ,
,
![]() .
.
1.
Е. В. Бурлаченко. Алгебраические заметки.
2. Риордан Д. Введение в
комбинаторный анализ. – М.: ИЛ, 1963.
3. Сачков В. Н.
Комбинаторные методы дискретной математики. – М.: Наука, 1977.