Е. В.
Бурлаченко
О ЧЕМ
ГОВОРЯТ «МЕТАЛЛИЧЕСКИЕ ПРОПОРЦИИ»?
«Металлической пропорцией» (в честь «золотой
пропорции») называется положительный корень уравнения ![]() :
:
 ,
, 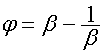 .
.
Отсюда видно, что если ![]() , то
, то ![]() . Следовательно,
. Следовательно,
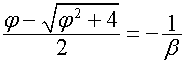 .
.
Так
как формула «металлической пропорции» являются частным случаем формулы корня
квадратного уравнения, она указывает на определенную связь квадратных уравнений
с гиперболическими функциями.
Полагая формальный степенной ряд самым красноречивым
алгебраическим объектом, переведем проблематику «металлических пропорций» на
язык степенных рядов.
Будем рассматривать формальный степенной
ряд с действительными коэффициентами как последовательность этих коэффициентов,
т.е. как элемент векторного пространства. Обозначим:
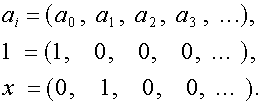
Матрицу ![]() и соответствующее ей
преобразование будем обозначать одним и тем же символом. Столбцы и строки матрицы
и соответствующее ей
преобразование будем обозначать одним и тем же символом. Столбцы и строки матрицы ![]() пронумеруем целыми
неотрицательными числами. Транспонированную к
пронумеруем целыми
неотрицательными числами. Транспонированную к
![]() матрицу обозначим
матрицу обозначим ![]() . Образ вектора
. Образ вектора ![]() при
преобразовании
при
преобразовании ![]() обозначим
обозначим ![]() .
.
Матрицу вида
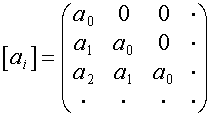 ,
,
( ![]() -й член
-й член ![]() -го столбца матрицы равен
-го столбца матрицы равен ![]() и нулю при
и нулю при ![]() ) назовем матрицей умножения на вектор
) назовем матрицей умножения на вектор ![]() . Тогда
. Тогда
![]() .
.
Обратным к ![]() назовем вектор
назовем вектор 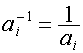 , определяемый уравнением
, определяемый уравнением
![]() .
.
Вектор
![]()
назовем ![]() -й степенью
-й степенью ![]() .Каждый вектор представим в виде
.Каждый вектор представим в виде
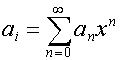 .
.
Матрицу, ![]() -й столбец которой является
-й столбец которой является ![]() -й степенью
-й степенью ![]() , назовем матрицей
степеней вектора
, назовем матрицей
степеней вектора ![]() и обозначим
и обозначим ![]() . Матрица степеней отображает произведение векторов на произведение
их образов:
. Матрица степеней отображает произведение векторов на произведение
их образов:
![]() .
.
Если ![]() и
и ![]() рассматривать как
функции
рассматривать как
функции ![]() и
и ![]() , то выражению
, то выражению ![]() соответствует
подстановка
соответствует
подстановка ![]() .
.
Обозначим:
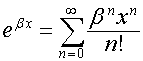 .
.
Векторы данного вида умножаются по правилу
![]() .
.
Произвольная степень формального степенного ряда
определяется следующим образом:
![]() ,
,
![]() ,
, ![]() .
.
Среди матриц степеней
особое место занимает матрица ![]() : транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
: транспонированную к ней матрицу можно рассматривать
одновременно как произведение матрицы степеней и матрицы умножения и как
трансформацию матрицы умножения:
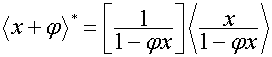 ,
,
![]() ,
,
где ![]() – диагональная матрица,
диагональные элементы которой равны значениям вектора
– диагональная матрица,
диагональные элементы которой равны значениям вектора ![]() :
:
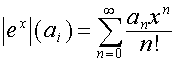 .
.
Например,
![]()
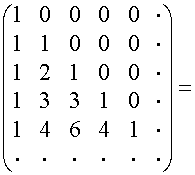
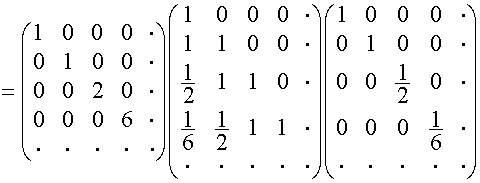 .
.
Обозначим:
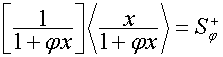 ,
,
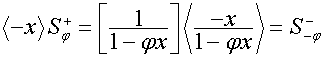 .
.
Тогда для вектора  имеем
имеем
![]() ,
,
![]() .
.
Преобразование
![]() является отражением:
является отражением:
![]() .
.
Пространство векторов, отображаемых
преобразованием ![]() на себя,
обозначим
на себя,
обозначим ![]() ; пространство векторов, отображаемых на противоположные,
обозначим
; пространство векторов, отображаемых на противоположные,
обозначим ![]() . Составляющие вектора
. Составляющие вектора ![]() в пространствах
в пространствах ![]() и
и ![]() соответственно равны:
соответственно равны:
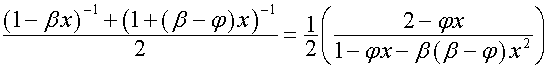 ,
,
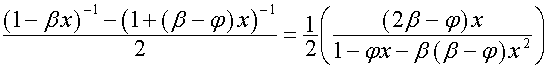 .
.
Векторы
![]() и
и 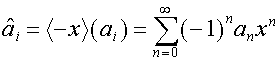 назовем спаренными.
Например,
назовем спаренными.
Например, ![]() спарен с
спарен с ![]() . Преобразование
. Преобразование ![]() векторы пространства
векторы пространства ![]() отображает на спаренные, векторы пространства
отображает на спаренные, векторы пространства ![]() – на противоположные спаренным.
– на противоположные спаренным.
Вектор ![]() ,
, ![]() , обладающий свойством
, обладающий свойством

обозначим
![]() . Его составляющие в пространствах
. Его составляющие в пространствах ![]() и
и ![]() обозначим соответственно
обозначим соответственно
![]() и
и 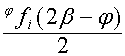 . Так как
. Так как
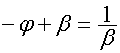 ,
,  ,
,
то
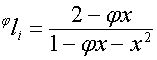 ,
, 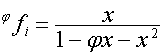 ,
,
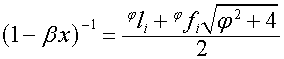 ,
,
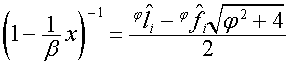 ,
,
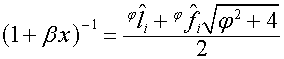 ,
,
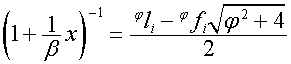 .
.
Рассмотрим
ряд
 .
.
Он является решением
уравнения
![]() ,
,
поэтому
![]() ,
,
где ![]() – целое число. Кроме
того
– целое число. Кроме
того
![]() ,
,
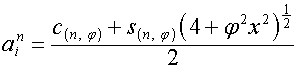 ,
,
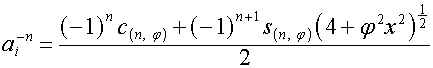 ,
,
где
![]() – полином степени
– полином степени ![]() , корни которого отличаются от корней полинома Чебышева
, корни которого отличаются от корней полинома Чебышева ![]() множителем
множителем ![]() :
:
![]() ,
,  ,
,
![]() – полином степени
– полином степени ![]() , корни которого отличаются от корней полинома Чебышева
, корни которого отличаются от корней полинома Чебышева ![]() множителем
множителем ![]() :
:
![]() ,
, ![]() ,
, 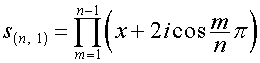 .
.
Пояснение: полиномы Чебышева
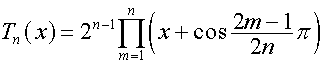 ,
, ![]() ,
,
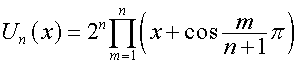 ,
, ![]()
определяются также следующим образом:
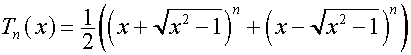 ,
,
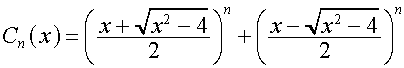 ,
,
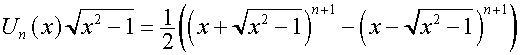 ,
,
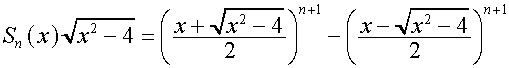 .
.
Отсюда видно, что
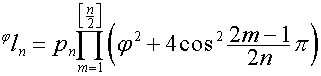 ,
, ![]() ,
, ![]() ,
,
или, если рассматривать ![]() как функцию
как функцию ![]() ,
,
![]() ;
;
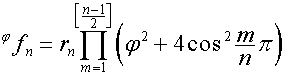 ,
, ![]() ,
, ![]() ,
,
![]() .
.
Так
как
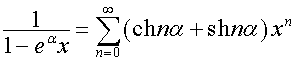 ,
,
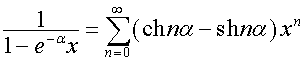 ,
,
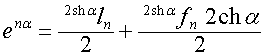 ,
,
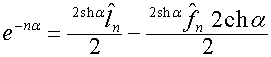 ,
,
то
![]() ,
, ![]() ,
,
![]() ,
, 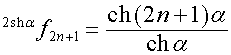 .
.
2
Рассмотрим аналогичный случай. Чтобы не усложнять символику
и подчеркнуть аналогию, будем пользоваться обозначениями из предыдущего
раздела.
Вектор ![]() ,
, ![]() , обладающий свойством
, обладающий свойством
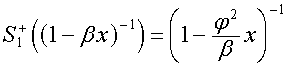 ,
,
обозначим
![]() . Его составляющие в пространствах
. Его составляющие в пространствах ![]() и
и ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и 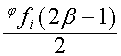 . Так как
. Так как
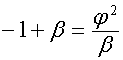 ,
, 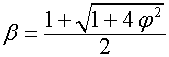 ,
,
то
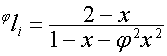 ,
, 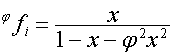 ,
,
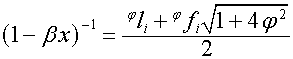 ,
,
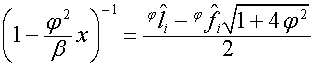 ,
,
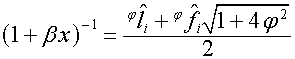 ,
,
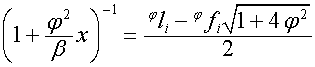 .
.
Рассмотрим
ряд
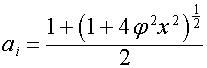 .
.
Он является решением
уравнения
![]() ,
,
поэтому
![]() .
.
Раскладывая ![]() в бином Ньютона и
группируя члены, можно представить его в виде
в бином Ньютона и
группируя члены, можно представить его в виде
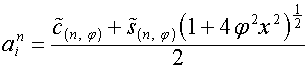 ,
,
где
![]() – полином степени
– полином степени ![]() (
( ![]() – целая часть от
– целая часть от ![]() ),
), ![]() – полином степени
– полином степени ![]() . Сравнивая алгоритм получения полиномов
. Сравнивая алгоритм получения полиномов ![]() и
и ![]() с алгоритмом получения
полиномов
с алгоритмом получения
полиномов ![]() и
и ![]() при разложении в бином
Ньютона
при разложении в бином
Ньютона
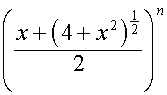 ,
,
заключаем,
что ![]() и
и ![]() получаются из
получаются из ![]() и
и ![]() перестановкой
коэффициентов в обратном порядке и понижением степени на единицу для
перестановкой
коэффициентов в обратном порядке и понижением степени на единицу для ![]() и
и ![]() . Например:
. Например:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Таким образом,
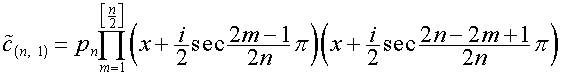 ,
,
где
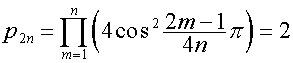 ,
,
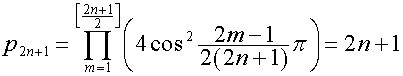 ;
;
(два
последних равенства не нуждаются в доказательстве, поскольку начальные члены
полиномов ![]() известны),
известны),
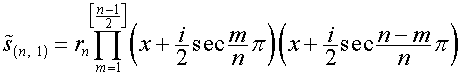 ,
,
где
![]() ,
, ![]() .
.
Так
как ![]() , или
, или
 ,
,
то
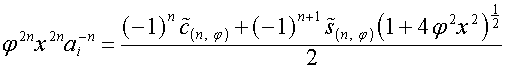 .
.
Отсюда видно, что
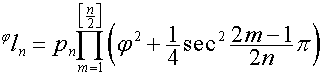 ,
, ![]() ,
,
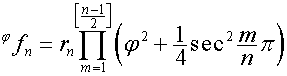 ,
, ![]() .
.
Так
как
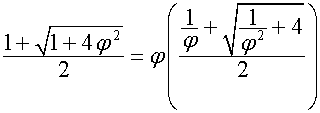 ,
,
то при ![]()
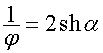 ,
, ![]() ,
,
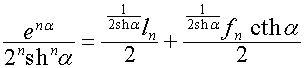 ,
,
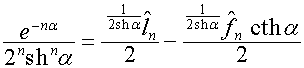 ,
,
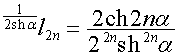 ,
, 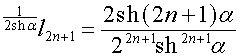 ,
,
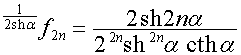 ,
, 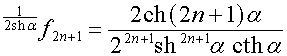 .
.
3
Рассмотрим
еще один аналогичный случай.
Вектор
![]() ,
, ![]() , обладающий свойством
, обладающий свойством
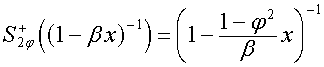 ,
,
обозначим ![]() . Его составляющие в пространствах
. Его составляющие в пространствах ![]() и
и ![]() обозначим
соответственно
обозначим
соответственно ![]() и
и ![]() . Так как
. Так как
 ,
, ![]() ,
,
то
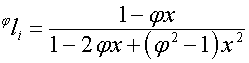 ,
, 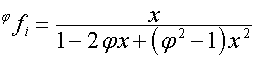 ,
,
![]() ,
, 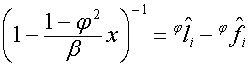 ,
,
![]() ,
, 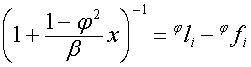 .
.
Рассмотрим
ряд
![]() .
.
Он обладает свойствами:
![]() ,
,
![]() ,
,
![]() ,
,
где
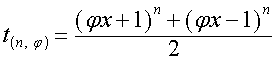 ,
, 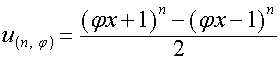 .
.
Найдем корни полиномов ![]() и
и ![]() .Обозначим:
.Обозначим:
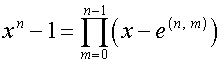 ,
,
![]() .
.
Тогда:
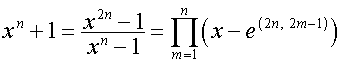 ,
,
 ,
,
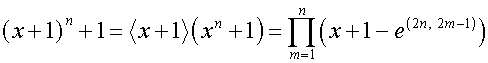 .
.
Переставляя
коэффициенты в обратном порядке, получаем:
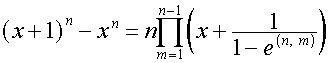 ,
,
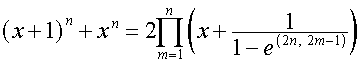 ,
,
где
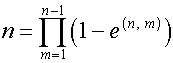 ,
, 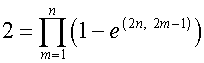 .
.
Так
как
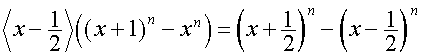 ,
,
то
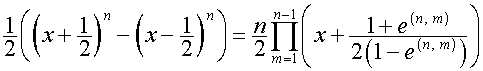 ,
,
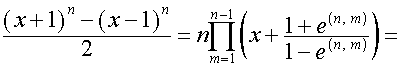
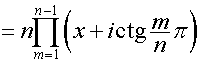 .
.
Аналогично
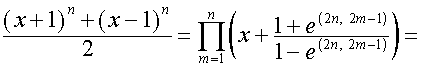
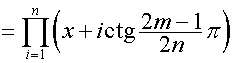 .
.
Таким
образом,
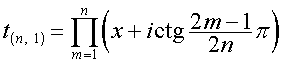 ,
,
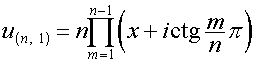 ,
,
![]() ,
, ![]() .
.
Так
как
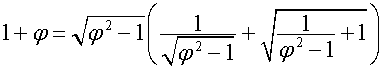 ,
,
то при ![]()
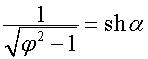 ,
, ![]() ,
,
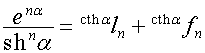 ,
, 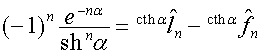 ,
,
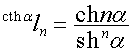 ,
, 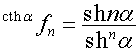 .
.
Так как
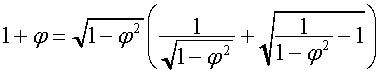 ,
,
то при ![]()
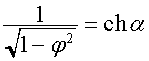 ,
, ![]() ,
,
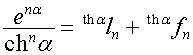 ,
, 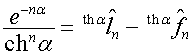 ,
,
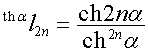 ,
, 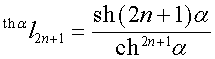 ,
,
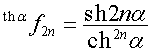 ,
,  .
.
Отметим, что
![]() ,
, ![]() .
.
***
Итак, мы видим, что в бесконечномерном векторном
пространстве формальных степенных рядов существует некий алгебраический
механизм, в котором векторы различных «видов» «работают» как притертые друг к
другу детали. «Металлическим пропорциям», воплощением которых служит ряд
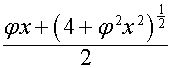 ,
,
отводится
если не центральная, то важная функциональная роль. Назначение и устройство
этого механизма нам не ясны, но, как всякий механизм, он может быть исследован
и понят вплоть до малейших деталей.
Литература.
Справочная
математическая библиотека. Математический анализ. Вычисление элементарных функций. М.,
Физматгиз, 1963., 248 стр.
Стахов А. П., Ткаченко И.
С. Гиперболическая тригонометрия
Фибоначчи. Доклады Академии наук Украины, 1993, № 7.
Стахов
А. П . Металлические Пропорции – новые
математические константы Природы. http://www.trinitas.ru/rus/doc/0232/004a/02321079.htm