Другие статьи

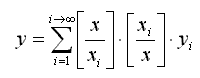
ТЕОРИЯ ЧИСЕЛ: ПРОСТЫЕ ЧИСЛА И УНИВЕРСАЛЬНОЕ УРАВНЕНИЕ

        А.М. Белов

    Для описания самых сложных и трудно поддающихся описанию формулами процессов и объектов может применяться универсальное уравнение:

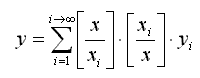
    где [ ] - (и далее по тексту) математический знак обозначающий целую часть числа.

    Известно, что в теории чисел на протяжении очень длительного времени не удается предложить формулу (в традиционном ее понимании и представлении) задающую последовательность простых чисел из-за непредсказуемости их появления в общей последовательности чисел. В настоящее время последовательности простых чисел описываются либо в виде баз данных (списков, таблиц, массивов) простых чисел, либо в виде компьютерных программ (алгоритмов) позволяющих находить простые числа по тем или иным правилам.

    Учитывая широкие возможности универсального уравнения можно ожидать, что  его применение позволит продвинуться в вопросе представления одной формулой последовательности простых чисел. Поскольку этот вопрос является весьма сложным ниже рассмотрены лишь возможные подходы к описанию последовательности простых чисел формулой, составленной на основе использования универсального уравнения.

     Самым простым и очевидным способом использования универсального уравнения при описании последовательности простых чисел является непосредственное задание этим уравнением последовательности простых чисел на основе таблицы известных простых чисел путем замены x¡ на порядковый номер n простого числа в последовательности простых чисел, а y¡ на значение этого простого числа:

    y=[n]·[1/n]·2 + [n/2]·[2/n]·3 + [n/3]·[3/n]·5 + [n/4]·[4/n]·7 + [n/5]·[5/n]·11 + [n/6]·[6/n]·13 +[n/7]·[7/n]·17+...

    При подстановке в такое уравнение какого либо порядкового номера n простого числа в общей последовательности простых чисел будет вычисляться значение простого числа соответствующее этому порядковому номеру. Это уравнение можно продолжать до бесконечности и очевидны его главные недостатки - значительный объем и большие затраты времени на выполнение вычислений с его использованием. Хотя вполне могут возникнуть ситуации его практического использования, например при нежелательности применения таблиц (массивов) простых чисел, использовании лишь фрагментов уравнения.  

    При использовании универсального уравнения совместно с малой теоремой Ферма  для задания числового ряда:

0 +  2 +  3 +  0 +  5 +  0 +  7 +  0 +  0 +  0 +  11 +  0 +  13 +  0 +  0 +  0 +  17 +  0 +  19 +  0 +  0 +  0 +  23 +  0 +  0 +  0 +  0 +  0 +  29 +  0 +  31 +  0 +  0 +  0 +  0 +  0 +  37 +  0 +  0 +  0 +  41 +  0 +  43 +  0 +  0 +  0 +  47 +  0 +  0 +  0 +  0 +  0 +  53 +  0 +  0 +  0 +  0 +  0 +  59 +  0 +  61 +  0 +  0 +  0 +  0 +  0 +  67 +  0 +  0 +  0 +  71 +...,

в котором все члены не равные простым числам равны нулю можно получить формулу существенно меньшего объема:

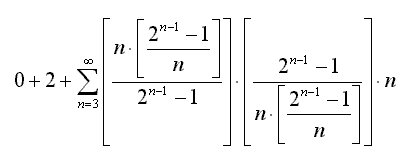
    Нетрудно заметить, что в этой формуле с ростом n слишком быстро будут расти объемы вычислений и используемые при вычислениях по формуле числа.

    Рост объема вычислений с увеличением n при формировании ряда можно несколько замедлить если при составлении формулы для вычисления членов ряда совместно с универсальным уравнением использовать тест простоты числа n заключающийся в проверке его на делимость на все простые числа меньшие, чем корень из n. При этом формула, задающая числовой ряд увеличится в объеме и будет иметь следующий вид:

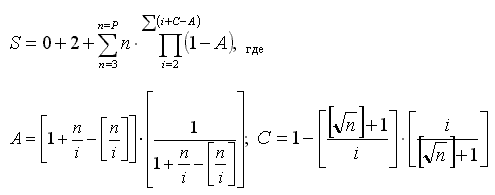
    P - порядковый номер выбранного предельного члена ряда. В этой формуле применение универсального уравнения обеспечило изменение верхнего предела произведения в ходе выполнения вычислений. 

    Для того, что бы посмотреть, как работает формула на форме в Visual Basic создайте кнопку и загрузите в нее следующий код, имитирующий использование формулы:  

    Изменяя в представленном коде значение P будете получать  значение ряда и частичную сумму ряда для N  от 0 до P. Причем представленный код полностью имитирует вычисления по формуле в ручную.

    Демонстрационную версию программы можно посмотреть на http://stob2.narod.ru/program/prost.htm.

    Если поэкспериментировать с рассматриваемой формулой, то не трудно будет заметить, что рассчитанное для любого n значение частичной суммы ряда будет находиться в окрестностях простого числа. Используя это свойство можно предложить следующую формулу для вычисления по заданному числу значения простого числа большего заданного:

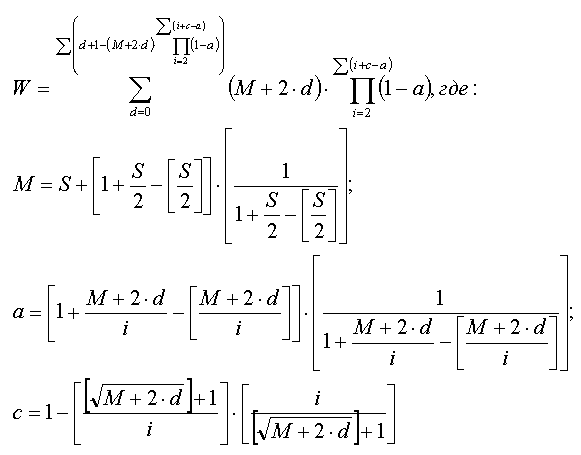
    Для того, что бы посмотреть, как работает формула на форме в Visual Basic создайте кнопку и загрузите в нее следующий код, имитирующий использование формулы: 

    Демонстрационную версию программы можно посмотреть на http://stob2.narod.ru/program/prost.htm.

    При изменении в представленном коде значения P в результате вычислений по программе будет получаться новое простое число W  большее P. Например, при подстановке значений Р в интервале от 641 до 647 по формуле можно вычислить ряд простых чисел, приведенных в таблице:

    Числа 641, 643, 647 являются простыми. Как видно из таблицы формула позволяет вычислить новые простые числа только для Р тоже простых.

    Необходимо учитывать, что сумма S всех простых чисел ряда от 1 до Р тем больше отличается от вычисленного W, чем больше Р и соответственно W. Исходя из этого для уменьшения объема вычислений в формулу можно ввести поправочные коэффициенты, зависящие от величины P и W.

    Необходимо еще отметить, что приведенные в этой статье программы не позволяют вычислять по настоящему большие числа. Для этого необходимо дополнительно использовать специальные методы работы на ПЭВМ с большими числами. В интернете быстро можно найти описание соответствующих методов и программ.

Можно еще посмотреть информацию на  http://zhurnal.lib.ru/editors/b/below_a_m/.