Другие статьи

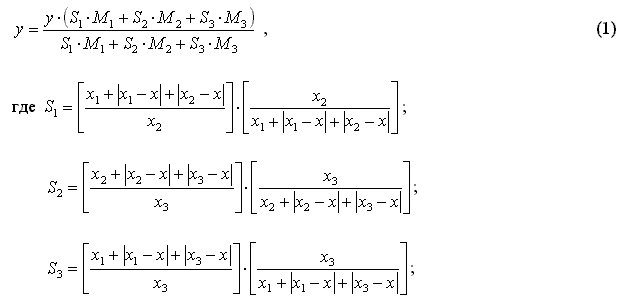
УРАВНЕНИЯ МНОГОУГОЛЬНИКОВ И СПИРАЛЕЙ НА ИХ ОСНОВЕ

        А.М. Белов                                  

Различные геометрические фигуры обычно описываются либо графически, либо словесными формулировками. Уравнения, не требующие при применении использования дополнительных словесных формулировок, существуют только для задания прямой, окружности, эллипса и фигур (линий), получаемых на их основе.  В число геометрических фигур для описания, которых используются уравнения не входят многоугольники.  Актуальность получения уравнений многоугольников определяется, прежде всего, их практически бесконечным разнообразием и повсеместным использованием объектов, имеющих форму различных многоугольников.

При этом конечно нельзя утверждать, что при описании многоугольников совсем не используются никакие уравнения. При описании многоугольников могут использоваться системы линейных уравнений, задающих прямые, но при этом эти системы линейных уравнений обязательно должны сопровождаться словесными описаниями, ограничивающими область применения каждого из входящего в систему уравнения или символами, обозначающими эти словесные описания. В противном случае график такой системы уравнений будет представлять собой не многоугольник, а несколько пересекающихся прямых линий. Это связано с тем, что линейное уравнение без соответствующих словесных пояснений не в состоянии определить отдельный отрезок или отдельную точку.

Таким образом, очевидно, что для составления уравнений многоугольников необходимо применять уравнения способные определить произвольный отрезок без использования при этом дополнительных словесных описаний.

Необходимыми свойствами обладает специальное уравнение ,  состоящее из суммы произведений: [ x/x_i ]*[ x_i/x]*y_i . В этом выражении: [ ] – знак, обозначающий целую часть числа и далее по тексту статьи предполагает выполнение процедуры по отбрасыванию дробной части числа ,  y_i  - значение функции при  значении аргумента x равном x_{i .} 

В работе [1] было показано, что на основе использования специального уравнения можно получить уравнения обеспечивающие определение отдельных отрезков или линий, состоящих из нескольких отрезков.

Далее приведены конкретные примеры уравнений многоугольников составленных на основе использования специального уравнения. В качестве примеров были выбраны треугольник и прямоугольник ориентированные по разному относительно координатных осей. Не имеющие сторон параллельных координатным осям и имеющие стороны параллельные координатным осям. Все уравнения других многоугольников будут иметь вид аналогичный виду приведенных ниже в качестве примеров уравнений.

Сформировать уравнения для других многоугольников можно так же по тем же правилам, что и для уравнения треугольника или прямоугольника. При этом различия уравнений для разных многоугольников будут выражаться в основном в их объеме. Чем больше сторон имеет многоугольник, тем больше объем его уравнения. Кроме этого необходимо отметить, что многоугольники ориентированные, так, что хотя бы одна их сторона оказывается параллельной оси y, могут быть представлены только в виде уравнения, задающего неявную функцию.  

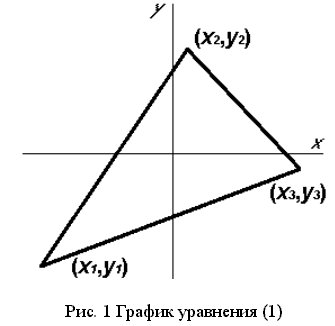
Произвольный треугольник, не содержащий ни одной стороны параллельной оси y, однозначно определяется в виде неявной функции, заданной уравнением (1). Решения уравнения (1) относительно x приведены в виде системы уравнений (2). График уравнения (1), построенный при значениях координат вершин треугольника x₁ = -175; x₂=20; x₃=170; y₁= -150;  y₂=140; y₃= -20 приведен на рис. 1.

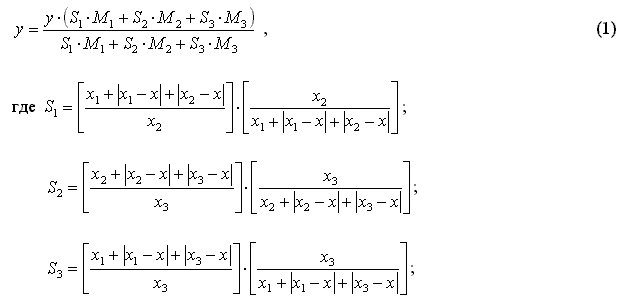
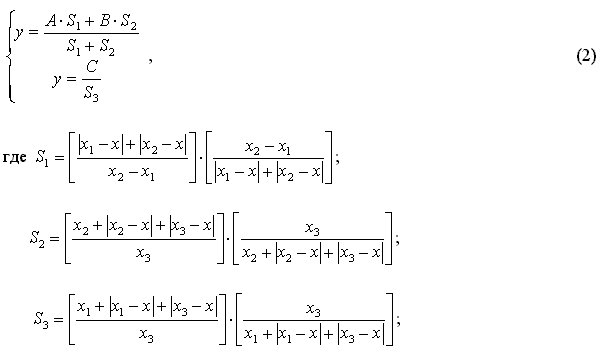
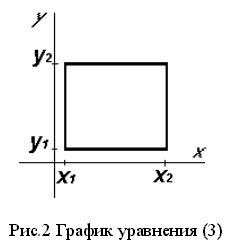
Произвольный прямоугольник, содержащий стороны параллельные оси y, определяется в виде неявной функции, заданной уравнением (3) для всех x и y>0. График уравнения (3), построенный при x₁ = 25; x₂=250;  y₁= 30;  y₂=220 приведен на рис. 2.

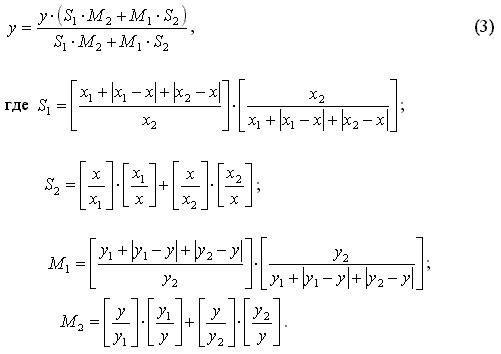
Уравнения многоугольников (1, 3) обеспечивают возможность составления уравнений треугольной и прямоугольной спиралей.

Треугольная спираль может быть определена системой уравнений (4). График системы уравнений (4) приведен на рис. 3.

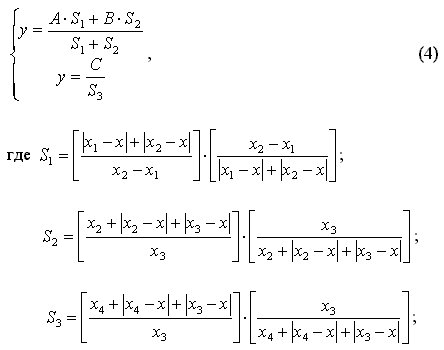
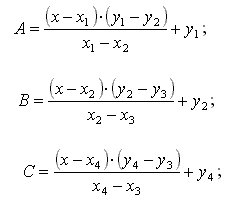
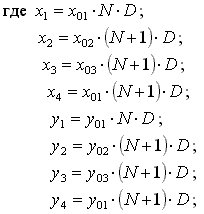
где x₀₁; x₀₂; x₀₃; y₀₁; y₀₂; y₀₃ – координаты вершин начального треугольника, начиная с которого начинает раскручиваться спираль; D – шаг спирали; N – номер витка спирали.

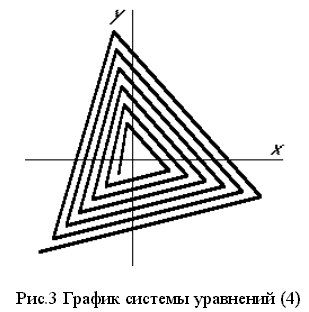
График системы уравнений (4) на рис. 3 был построен при x₀₁= -5; x₀₂= -1; x₀₃=7; y₀₁= -5; y₀₂=7; y₀₃= -2; D=7.

Необходимо отметить, что система уравнений (4) не является универсальной. Так она не определяет спираль, если у начального треугольника одна из его сторон будет параллельна оси y и в ряде других случаев, касающихся в основном положения вершин начального треугольника относительно осей координат.

Прямоугольная спираль может быть определена уравнением (5) для всех x и y>0. График системы уравнений (5) приведен на рис. 4.

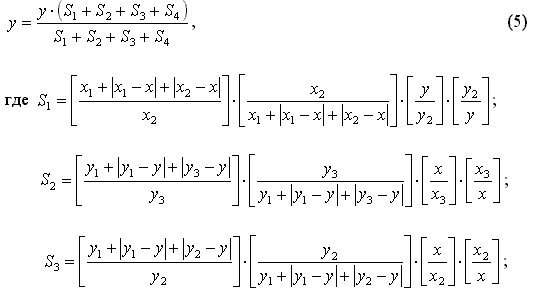
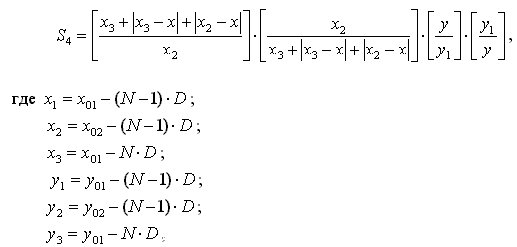
где x₀₁; x₀₂ и y₀₁; y₀₂ – соответственно координаты, определяющие ширину и высоту начального прямоугольника, начиная с которого начинает раскручиваться спираль; D – шаг спирали; N – номер витка спирали.

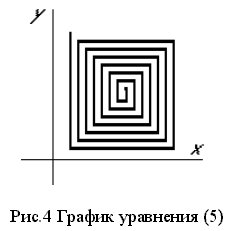
График уравнения (5) на рис. 4 был построен при x₀₁= 145; x₀₂= 160; y₀₁= 145; y₀₂=170; D=7.

            Приведенные примеры показывают принципиальную возможность задания аналитическим способом уравнений многоугольников и спиралей на их основе.

            Необходимо отметить, что в уравнениях (1), (3) и (5) нельзя производить дальнейшие сокращения точно так же, как нельзя заменять выражение x/x на 1, если допускается, что х может быть равно нулю.

            Приведенные уравнения спиралей можно рассматривать так же, как уравнения, задающие фракталы, так как  каждый виток спирали по форме повторяет предыдущие, имея различия лишь в размерах, т. е. спирали имеют все основные свойства фракталов. 

    Литература

            1. Белов А.М. К вопросу задания в аналитическом виде ступенчатых и импульсных функций. http://www.laboratory.ru.