Synergetics. Etudes 70.
Is Dedicated to Centennial of Burthday of Outstanding Scientist,
Professor
Basin Abram M.
Basina G. I., Basin M. A.
SIC ”Synergetics” of Saint-Petersburg Association of Scientist and
Scholars.
Etude 4.
Many-dimensional Power Complex Systems
of Iterative Relations. Exponent of Circumference as One of Forms of
Fundamental Decision of the System.
December 18, 2009.
At the
decision of nonlinear many-dimensional problems of dynamics of complex systems
essentially role play complex operators, which may be called power operators.
We consider many-dimensional iterative symbolic relation:
.
(1)
Here 
- aggregate of spiral complex coordinates;
(2)
is the
linear complex operator, which elements are algebraic complex numbers (See
Etude5).
Relation
(1) is symbolic representation of formula:
.
(3)
We take logarithm
from left and right parts of equality (3)
,
(4)
or in
operator form –
.
(5)
We
introduce the next designation:
.
(6)
Then
equation (5) will be written in the form:
,-
(7)
and the
equality(4) – in the form:
.
(8)
We
introduce complex finite-dimensionally affine complex vector space. As the vector
in our complex space we shall consider the aggregate of complex numbers;
transforming for the relation (8)
. (9)
We
consider, that the space is related to determined orts:
.
(10)
So
. (11)
We call
equalities (7), (8) as linear transformation of vector 
to the vector 
.
If the
determinant of matrix 
is not equal to zero, then
solving equations (7), (8) relatively we receive:
,
(12)
where
matrix 
has elements:
.
(13)
Here 
is
determinant of matrix , and 
are its algebraic addendums in relation to
elements 
.We
introduce new orts:
.
(14)
Connection
between the new and old orts expresses with relations:
.
(15)
Determinant
of matrix
(16)
is not
equal to zero. If any vector in system of coordinates with orts (10) had
the components 
, then in new
coordinates system it will have another components
, (17)
which
express through the first with help of relations
.
(18)
Here the
matrix 
is transposed relative . If we have
any iterative process, which in primary coordinate system was expressed with formula
(7), then in the new coordinate system the same process will be expressed with
the formula
,
(18)
where
.
(19)
Matrix
(20)
is called
similar to the matrix [1]. Similar matrixes are equivalent in that
relation, that they determine the same transformation, but represented in
different systems of coordinates. If the determinant of matrix is not equal to zero, then through the
matrixes 
are diagonal matrixes [1],
for which are not equal to zero only diagonal members. In the case of choice of
transformation 
with such a matter, that matrix will be diagonal matrix, then relation (18)
will transform in complex one-dimensional iteration relations
,
(21)
where 
-are
diagonal members of matrix .
.
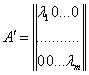(22)
For the
finding of corresponding matrix and diagonal members of matrix we write the next equality:
,-
(23)
or in the
coordinate form:
. (24)
If we take
the elements 
as components of any vector 
, then we
can write the equality (24)in the form of vector equality
. (25)
«So we see,
that finding of matrix , which
reduces the matrix to the diagonal form consists in finding such
vectors , which
reproduce with the accuracy of complex number factor as a result of linear
transformation, determining by matrix . This fact
is algebraic analog of that fact of contemporary quantum mechanics, according with
which the matrix mechanics of Heisenberg is equivalent to wave mechanics of
Schrödinger. According to the first point of view essential problem is the
transformation of any matrix (infinite) to the diagonal form. As concerns the
wave mechanics, here essential question
is the problem of finding such vectors (in the space with infinite number of
dimensions), which reproduce with the accuracy of number factors the result of
any linear transformation. Former considerations we called algebraic analog that’s
why, when we bound with finite number of dimensions, we lead our problems to
pure algebraic problems. In more complex cases with infinite variety of
dimensions we go out from the frames of usual algebra and we need to use the
apparatus of analysis [1].
System
(24)or (25) may be written in the form:
.
(26)
Here 
is single matrix. For becoming of the
decision, which is not equal to zero the determinant of matrix 
must be equal to zero
.
(27)
We received
characteristic complex algebraic equation of the 
- order,
which has equal complex decisions. Suppose that these
decisions are different. So we find all meanings of 
and may to build the matrix
,
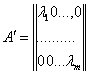(28)
and instead
of iteration system (12) to decide the one-dimensionally iterative relations
(21), which we have considered in Etude
¹3. We must now to determine with the accuracy of any complex multiplier not
equal to zero the elements of matrix 
. In the
system (26) we take any meaning of one of coordinates of vector 
and transfer
any members from left part in the right part of the system (26), excluding one
of equations. If receiving in this case multivendor system of equations has
determinant not equal to zero, than its decision determines with formula of
Kramer [1]. This procedure repeats for all meanings of . We return
to the system of iterative relations (21). Substituting consecutive in the
right part the meanings of 
as far as 
, we
receive:
.
(29)
Equality(29)determines
fundamental decision of system (21).We introduce new complex varieties
.
(30)
Then the
system (29) will be written in the form
. (31)
Exponentiating
(31), we receive
.
(32)
If has the
modulus, equal to 1, than the meanings of
for all whole meanings of 
lay on the exponent of circumference (see
Etudes 1-3). We may introduce the exponential vector
.
(33)
Then the
relation (32) may be written in symbolic form:
.
(34)
Relation
(31) may be written in the form
(35)
Last
relation is written in the term of affine vectors and classical matrixes. Shall
we return in relation (35) to primary coordinate system, using the relations
(18)-(20)
. (36)
Or
.
(37)
Exponentiating (37), we receive symbolic decision of system
(1)
.
(38)
Between coordinates of exponential vector 
realizes the
connection according the relation 
,
(39)
or in
coordinate form –
(40)
Literature.
1. Smirnov
V. I. Curse of High Mathematics for Techniques and Physicists. B. 3 “GITTI”M.-_L..
1933. 736 p.