Синергетика.
Этюды 70.
Посвящено
100-летию со дня рождения выдающегося учёного, профессора
Басина Абрама Моисеевича.
Басина
Г. И., Басин М. А.
НИЦ
«Синергетика» Санкт-Петербургского союза учёных.
Этюд 4
Многомерные
степенные комплексные системы итерационных соотношений.
Экспонента
окружности как одна из форм фундаментального решения системы.
8 декабря
2009г.
При решении нелинейных многомерных проблем динамики сложных систем особую роль играют комплексные операторы, которые могут быть названы степенными. Рассмотрим символьное многомерное итерационное соотношение:
.
(1)
Здесь 
- совокупность
спиральных комплексных координат;
- (2)
линейный комплексный оператор, элементами которого являются алгебраические комплексные числа.(смотри Этюд 5). Соотношение (1) соответствует системе уравнений:
. (3)
Прологарифмируем левую и правую части равенства (3):
(4)
или в векторно - операторном виде:
.
(5)
Введём следующее обозначение:
.
(6)
Тогда уравнение (5) запишется в виде:
,
(7)
а равенство (4) –в форме:
.
(8)
Введём в рассмотрение комплексное конечномерное аффинное векторное пространство. Вектором будем считать совокупность алгебраических комплексных чисел:
. (9)
Считаем, что пространство отнесено к определённым ортам:
.
(10)
Так что
. (11)
Равенства (7), (8) назовём линейным преобразованием вектора 
к вектору
.
Если определитель матрицы 
отличен от нуля, то,
решая уравнения (7), (8) относительно , получаем
,
(12)
где матрица 
имеет элементы
.
(13)
Здесь 
-определитель матрицы , а 
алгебраические дополнения
его относительно элементов 
. Введём в рассмотрение новые орты:
.
(14)
Связь между старыми и новыми ортами выражается с помощью соотношений:
. (15)
При этом определитель матрицы
(16)
считаем не равным нулю. Если некоторый вектор в системе координат с
ортами (10) имел составляющие , то в новой системе координат он будет иметь другие
составляющие
, (17)
которые выражаются через предыдущие при помощи соотношения:
.
(18)
Здесь матрица 
транспонирована по
отношению к матрице . Если мы имеем некоторый линейный итерационный процесс,
который в первоначальной системе координат выражался формулой (7), то в новой
системе координат это же преобразование
будет выражаться формулой
, (18)
где
.
(19)
Матрица
(20)
называется подобной матрице . Подобные матрицы равносильны в том отношении, что они
представляют одно и то же преобразование пространства, но выраженное в
различных координатных системах. Если определитель матрицы отличен от нуля, то
среди матриц 
имеются диагональные
матрицы [1], у которых отличны от нуля только диагональные члены. В случае
выбора преобразования 
таким образом, что
матрица станет диагональной,
соотношение (18) разобьется на комплексные одномерные итерационные соотношения
типа
,
(21)
где 
-диагональные члены матрицы .
.
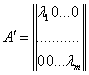(22)
Для отыскания соответствующей матрицы и диагональных членов
матрицы выпишем следующее
равенство:
(23)
или в координатной форме
.
(24)
Если рассматривать элементы 
как составляющие
некоторого вектора 
, то можно записать равенство (24) в виде векторного
равенства
.
(25)
«Мы видим таким образом, что разыскание матрицы , которая приводит матрицу к диагональной форме
сводится к разысканию таких векторов , которые воспроизводятся с точностью до численного множителя
в результате линейного преобразования, определяемого матрицей . Этот факт является алгебраическим аналогом того факта
современной квантовой механики, согласно которому матричная механика
Гейзенберга по существу равносильна волновой механике Шредингера.
Согласно первой точке зрения, существенным вопросом является задача приведения некоторой матрицы (бесконечной) к диагональной форме. Что же касается волновой механики, то здесь существенным вопросом является задача отыскания таких векторов (в пространстве с бесчисленным множеством измерений), которые бы воспроизводились с точностью до численного множителя в результате некоторого линейного преобразования. Предыдущие соображения мы назвали алгебраическим аналогом потому, что, ограничиваясь пространством с конечным числом измерений, мы приводим наши задачи к чисто алгебраическим задачам. В более же сложных случаях с бесчисленным множеством измерений мы существенно выходим из рамок обычной алгебры и нуждаемся в аппарате анализа» [1].
Система (24) или (25) может быть записана в виде:
.
(26)
Здесь 
- единичная матрица.
Для получения отличного от нуля результата определитель матрицы 
должен быть равен
нулю, то есть:
. (27)
Таким образом, мы получили характеристическое комплексное
алгебраическое уравнение 
-ого порядка относительно
, которое имеет ровно комплексных
решений. Предположим, что эти решения
различны. Найдя все значения , мы можем построить матрицу
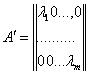(28)
и вместо системы итераций (12) решать одномерные итерационные соотношения (21), которые уже рассматривались нами в Этюде №3.
Нам осталось теперь определить с точностью до произвольного
не равного нулю комплексного постоянного множителя элементы матрицы 
. Для этого в системе уравнений (26) зададим произвольно
какую-либо координату вектора 
и перенесём
соответствующие ей члены левой части
уравнения (26) в правую часть, отбросив одно из уравнений. Если в этом
случае получившаяся неоднородная система уравнений на единицу меньшего порядка
имеет определитель, не равный нулю, то решение определяется по формулам Крамера
[1]. Эта процедура повторяется для всех значений . Вернёмся к системе итерационных соотношений (21).
Подставляя последовательно в правую часть значения 
вплоть до 
, получим
.
(29)
Равенство (29) определяет фундаментальное решение системы итерационных соотношений (7). Введём новые комплексные переменные:
. (30)
Тогда система (29) запишется в виде:
.
(31)
Потенцируя (31) , получим:
.
(32)
Если комплексная величина с
модулем равным единице, то значения 
при любых целых
значениях 
лежат на экспоненте
окружности (смотри Этюд №3). Таким образом, экспонента окружности, бифуркации
которой были рассмотрены нами в Этюде №1, является одной из фундаментальных форм фазовой траектории для
достаточно общей системы степенных итерационных соотношений. В ортогональной
системе координат можно ввести понятие экспоненциального вектора:
.
(33)
Тогда соотношение (32) может быть записано в символьном виде:
.
(34)
Соотношение (31) может быть записано в форме:
.
(35)
Последнее равенство записано уже в терминах аффинных векторов и классических матриц. Вернёмся в соотношении (35) к первоначальной системе координат, воспользовавшись соотношениями (18)-(20)
(36)
или
.
(37)
Потенцируя (37), получим решение системы (1) в символьной форме
.
(38)
Между координатами экспоненциального вектора 
осуществляется связь согласно соотношению
.
(39)
Или в координатной форме
.
(40)
Литература
1.Смирнов В. И. Курс высшей математики для техников и физиков . Том 3 ГИТТИ М.-Л. 1933 736 с.