Synergetics. Etudes 70.
Is Dedicated to Centennial of Burthday
of Outstanding Scientist, Professor
Basin Abram M.
Basina G. I., Basin M. A.
SIC ”Synergetics” of Saint-Petersburg
Association of Scientist and Scholars.
Etude 3.
Exponent of Circumference as the Phase
Trajectory of Nonlinear Iteration Relation.
2 December 2009
In this etude
are determined criteria of equivalence of complex differential equation of
first order and nonlinear iteration. Conditions, at which the points,
corresponding to the decision of iterative relation, lay on the exponent of
circumference, are determined.
At the investigation of dynamically
systems may be introduced the complex parameter of wholeness, found and solved
complex usual differential equation, to which it satisfies:
.
(1)
Here 
may be complex algebraic
variable
or complex spiral variable
. Family of phase
trajectories, which are the aggregate of decisions of equation (1), may be
represented in the form:
, (2)
where 
- the meaning
of complex coordinate of phase trajectory passing through the point 
at the moment of time 0. This
decision may be written and in spiral variables:
. (3)
Shall we
build iteration relation equivalent to the described dynamically systemå. Shall we solve equations (2, 3) to
the relation of 
:
. (4)
Suppose,
that we know the condition of one-dimensional complex dynamically system in
moment 
, corresponding
to the point 
and want to determine the
condition of the same system 
at the
moment 
. Then, using
former formulas, we shall receive:
. (5)
We shall
introduce the operator
:
. (6)
Operator generates the
iteration process and shows transformation of condition of dynamically systemat the
moment of time in its condition 
at the
moment
.
(7)
The last equation
describes discrete system, equivalent to the continuous dynamically system.
It is another method of undergoing
from continuous model to the discrete model. Shall we write instead of system (1)
the approximate system
,
(8)
which,
after series of transformations, becomes the form:
. (9)
Operators and 
are not equivalent:
one aspirates to another at the attention of 
to zero. Shall
we consider one practically important particular case. As the base equation
shall we take linear complex equation
.
(10)
Decision of
this equation has the form:
. (11)
Finally we receive
iterative relation:
.
(12).
So, in the case
of constant time interval, the iterative process of the first type, satisfying the
equalities (5-7), represents geometric series at the area of complex numbers.
If the value 
is imaginary, then all
members of series (12) lay on the circumference with radius
.
Iterative
process (9) in our particular case becomes the form:
.
(13)
Formulas
(12) and (13) coincide only in limiting case at
.
In the case
of finite meanings of 
these iterative
processes distinguish one from another then more as greater is the modulus of
value. But in the
second case we also have the geometric series. Shall we introduce in
consideration new complex variable:
. (14)
Then the
equation (1) transforms in the form:
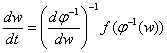,- (15)
and corresponding
iterative processes have the next form:
. (16)
Last equation
describes iterative process, which is equivalent to the equation (15).
Another, approximate
variant of iterative process, corresponding to the equation (15), has the form:
.
(17)
In considered
earlier particular case of linear differential equation shall we take, that the
relation of new variable from old variable has the form
.
Then the iterative
relation (12) after the series of transformations shall have the form
.
(18)
Iterative process
(18) in the right part of equation has the power function with complex power
coefficient. For the adequate description of such functions must be introduced
the representation of the field of spiral complex numbers. If the value is the imaginary number, then
all points of iteration process (18) lay on one of exponents of circumference,
which parameters determine by the meaning of 
.
Second type
of iteration process gives the next equality:
.
(19)
In this case
we also have in the right part of equation (19) the power function with complex
index of power, but the points of this iteration process lay on the exponent of
circumference only in the case of
imaginary meaning of and
aspirating of its modulus to zero.