Другие статьи

---

Синергетика. Этюды 70.

Посвящено 100-летию со дня рождения выдающегося учёного, профессора

Басина Абрама Моисеевича.

Басина Г. И., Басин М. А.

НИЦ «Синергетика» Санкт-Петербургского союза учёных.

Этюд 3

Экспонента окружности как фазовая траектория нелинейного итерационного соотношения.

02 декабря 2009

В настоящем этюде установлены критерии эквивалентности комплексного дифференциального уравнения первого порядка и нелинейного итерационного соотношения. Установлены условия, при которых точки, соответствующие решению итерационного соотношения, лежат на экспоненте окружности.

При исследовании динамических систем может быть введён комплексный параметр целого, найдено и решено комплексное обыкновенное дифференциальное уравнение, которому он удовлетворяет:

. (1)

Здесь может быть комплексной алгебраической переменной или комплексной спиральной переменной . Семейство фазовых траекторий, являющихся совокупностью решений уравнения (1), может быть представлено в виде:

,- (2)

где - значение комплексной координаты фазовой траектории, проходящей через точку в момент времени 0. Это решение может быть записано и в спиральных переменных:

. (3)

Построим итерационное соотношение, эквивалентное описанной динамической системе.

Разрешим равенства (2, 3) относительно :

. (4)

Предположим, что мы знаем состояние одномерной комплексной динамической системы в момент , соответствующее точке , и хотим определить состояние той же системы в момент . Тогда, воспользовавшись предыдущими формулами, получим:

. (5)

Введём понятие оператора :

. (6)

Оператор порождает итерационный процесс и указывает преобразование состояния динамической системы в момент времени в её состояние в момент времени

. (7)

Последнее уравнение описывает дискретную по отношению к времени систему, полностью эквивалентную непрерывной динамической системе.

Существует ещё один способ перехода от непрерывной модели к дискретной. Вместо системы (1) запишем приближённую систему

, (8)

которая, после ряда преобразований, приводится к виду:

. (9)

Операторы ине эквивалентны и один сходится к другому при стремлении к нулю.

Рассмотрим один практически важный частный случай. В качестве основного примем линейное комплексное уравнение

. (10)

Решение этого уравнения имеет вид:

. (11)

Окончательно получаем итерационное соотношение:

. (12).

Тем самым, в случае постоянного временного интервала итерационный процесс первого типа, удовлетворяющий равенствам (5-7), представляет собой геометрическую прогрессию в области комплексных чисел. Если величина является мнимой, то все члены ряда (12) лежат на окружности радиуса.

Итерационный процесс (9) в нашем частном случае примет вид:

. (13)

Формулы (12) и (13) совпадают лишь в пределе при . В случае конечных значений итерационные процессы отличаются друг от друга тем более, чем больше модуль величины .

Далее введём в рассмотрение новую комплексную переменную:

. (14)

Тогда уравнение (1) преобразуется к виду:

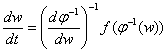,- (15)

а соответствующие итерационные процессы будут иметь следующий вид:

. (16)

Последнее уравнение описывает итерационный процесс, эквивалентный уравнению (15).

Другой, приближённый вариант итерационного процесса, соответствующий уравнению (15), имеет вид:

. (17)

В рассмотренном ранее частном случае линейного дифференциального уравнения примем, что зависимость новой переменной от старой имеет вид .

Тогда итерационное соотношение (12) после ряда преобразований примет форму

. (18)

Итерационный процесс (18) в правой своей части содержит степенную функцию с комплексным показателем степени. Для адекватного описания таких функций необходимо ввести представление о спиральных комплексных числах, которое даётся в этюде 5. В случае, если величина представляет собой мнимое число, все точки итерационного процесса (18) лежат на одной из экспонент окружности, параметры которой определяются значением .

И, наконец, второй тип итерационного процесса даёт нам следующее равенство:

. (19)

В данном случае мы также имеем в правой части уравнения (19) степенную функцию с комплексным показателем степени, однако члены итерационного процесса ложатся на экспоненту окружности только в случае мнимых значений и стремления модуля этой величины к нулю.