Synergetics. Etudes 70.
Is Dedicated to Centennial of Burthday of
Outstanding Scientist, Professor
Basin Abram M.
Basina G. I., Basin M. A.
SIC ”Synergetics” of Saint-Petersburg
Association of Scientist and Scholars.
Etude 2.
Exponents of Circumference as Phase
Curves of Nonlinear Dynamically Systems
20 November 2009
At the
investigation of dynamically systems for the determination of their integral
parameters we recommend the introduction of complex parameter of wholeness and
also finding and decision of complex differential equation, to which it
satisfies.
,
(1)
where 
may be complex algebraic variable 
or complex spiral variablle 
. Phase
trajectory which is the decision of equation (1), may be written in the form
, (2)
where 
is the
meaning of algebraic complex coordinate of phase trajectory, passing through
the point 
at the moment of time 
. The same
decision may be written and in spiral varieties.
. (3)
Shall we
introduce new function 
.
Then the
equation (1) will transform in the form 
, or
.
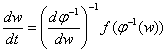(4)
Corresponding
phase trajectory for variable quantity 
has the form:
So, having
the decision of one equation (1), we may build the class of derivative
nonlinear differential equations, connected with given equation, which
decisions are building on the base of decision of given equation. It is
interesting one important particular case of fulfilled transformations. As the
main equation we take the linear complex
differential equation
.
(5)
Its
decision may be received with such a matter.: 
.
Integrating both parts of received equation, we shall receive: 
. Exhibiting
both parts of received equation, we receive: 
. If 
, then 
, and phase
trajectories of decision of this equation have the form
.
(6).
Shall we
represent: 
. Then the
decision of the equation (5) shall receive the form:
.
(7)
Phase
curves represent the developing or twisting spirals, or coming to zero, or
going away on the infinity. Further us will be interesting the particular case,
corresponding to 
. In this
case we have 
. If we
shall consider, not losing the generality, that the primary meaning of the
unknown quality is the real number 
, then the
equation of phase trajectory has the form:
.
(8)
The point
of phase trajectory of the equation (5) in considerable particular case moves
on the circumference with radius 
- on the
cyclic trajectory. Further shall we take that the connection between complex
variables and has the form
(9).
Then the
equation, describing the dynamics of variable receives the form: 
, or
.
(10)
This
equation we met at the investigation of dynamics of populations.
Cyclic
phase trajectories of dynamically system, describing with this equation, have
the form 
The last
equality describes the trajectory of the point, moving on the exponent of
circumference (See Etude ¹1). So, the exponent of circumference is a cyclic
phase trajectory of any dynamically system, describing with complex
differential equation (10).
But with
this not exhaust the class of differential equations, having phase trajectories
with the type of exponent of circumference. It is known that in dynamically
systems of different type occurs the bifurcation of cycles birth. If we shall
consider the variables of these systems as the logarithms of any new variables,
then for these new variables we receive the equations, for which the
bifurcation of cycles birth shall transform in the bifurcation of the birth of
any new trajectory which is the exponent of circumference.
The
undergoing from cyclic phase trajectory to the phase trajectory in the form of
the exponent of circumference must be standard for self organizing information-
transport systems, which have different but strongly connected dimensions of
variables, describing them.