Синергетика.
Этюды 70.
Посвящено
100-летию со дня рождения выдающегося учёного, профессора
Басина Абрама Моисеевича.
Басина
Г. И., Басин М. А.
НИЦ
«Синергетика» Санкт-Петербургского союза учёных.
Этюд 2
Экспоненты
окружности как фазовые кривые нелинейных динамических систем
20 ноября 2009
При исследовании динамических систем для определения динамики их интегральных параметров нами рекомендуется введение комплексного параметра целого, а также отыскание и решение комплексного обыкновенного дифференциального уравнения, которому он удовлетворяет,
,
(1)
где 
может быть комплексной
алгебраической переменной 
или комплексной
спиральной переменной 
. Фазовая траектория, являющаяся решением уравнения (1),
может быть записана в виде
,
(2)
где 
- значение алгебраической комплексной координаты фазовой траектории,
проходящей через точку 
в момент времени 
. Это же решение может быть записано и в спиральных
переменных.
(3)
Введём новую функцию 
.
Тогда уравнение (1)
преобразуется к виду 
или
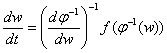(4)
Соответствующая фазовая траектория для переменной 
имеет вид:
Таким образом, имея решение
одного уравнения (1) мы можем построить класс производных нелинейных
дифференциальных уравнений, связанных с данным, решения которых строятся на
основе решения первого. Нас в дальнейшем
будет интересовать один важный частный случай выполненных преобразований.
В качестве основного уравнения примем линейное комплексное
уравнение.
.
(5)
Его решение может быть получено следующим образом: 
.
Интегрируя обе части последнего равенства, получаем: 
.
Экспонируя получившееся уравнение, получим 
.
Если 
,то 
, и фазовые траектории решения этого уравнения имеют вид
.
(6).
Представим 
. Тогда решение уравнения (5) примет форму:
(7)
Фазовые кривые представляют собой
развёртывающиеся или скручивающиеся спирали либо сходящиеся к нулю, либо
уходящие на бесконечность. В дальнейшем нас будет интересовать частный случай
когда 
. В этом случае 
. Если считать, не теряя общности , что начальное значение
неизвестной является действительным числом
, то уравнение фазовой кривой имеет вид
(8)
Точка фазовой кривой уравнения (5) в рассматриваемом частном
случае движется по окружности радиуса 
.- то есть по циклической траектории. Далее примем, что связь
между комплексными переменными и имеет вид:
. (9).
Тогда уравнение, описывающее динамику переменной примет форму 
или
(10)
Это уравнение встречается при
исследовании динамики популяций. Циклические фазовые траектории динамической
системы, описываемой этим уравнением, имеют
вид 
Последнее выражение описывает траекторию в виде экспоненты окружности.(смотри Этюд №1). Таким образом, экспонента окружности является циклической фазовой траекторией некоторой динамической системы, описываемой комплексным обыкновенным дифференциальным уравнением (10). Однако, этим не исчерпывается класс уравнений, имеющих фазовые траектории типа экспоненты окружности. Известно, что в ряде динамических систем происходит бифуркации рождения цикла. Если переменные, входящие в эти системы рассматривать как логарифмы некоторых новых переменных, то для этих новых переменных получаются уравнения, для которых бифуркация рождения цикла превратится в бифуркацию рождения новой фазовой траектории, являющейся экспонентой окружности. Переход от циклической фазовой траектории к фазовой траектории в виде экспоненты окружности, по-видимому, является стандартным для самоорганизующихся информационно-транспортных систем, имеющих подсистемы с сильно отличающимися друг от друга но связанными между собой масштабами описывающих их переменных.