Vortex - wave resonance
G. I.
Basina
M. A.
Basin
Scientific Research Center “Synergetics” of
Saint-Petersburg Association of Scientists and Scholars.
Mailing
Address:
Universitatskaya nab., 5 , Office 300
E-mail: basinm@yandex.ru.
ABSTRACT
At
the investigation of bodies, nonsymmetrical
streamlined by a liquid of variable density we revealed new phenomenon,
called by us “vortex - wave resonance”.
The essence of this phenomenon consists in resonant non-linear interplay between
dispersing waves and demarcations of environments , arising in continuum, and
vortical patterns forming near to a body. Resonance interaction results in
qualitative change of flow around the body, formation of new vortex - wave patterns and abnormal
change of the hydrodynamic forces, acting on a nonsymmetrical body.
THEORETICALLY
INVESTIGATIONS
The vast literature
[1] is dedicated to research of wave motions in continuum. In spite of that the
theoretically analysis of linear models of wave currents in non uniform mediums
does not indicate on presence of any resonant interaction of arising wave
motions among themselves, however, last decades by a number of the scientists
was opened and widely investigated resonant interplay non-linear surface and
internal gravitational wave motions. By Î. M. Phillips , Ì. S. Longuet-Higgins,
D. Benney, V.E. Zacharov, A. B. Shabbat, L. M.Brekhovskich and his group, G.B.
Whitham and other explorers was
theoretically predicted , and then experimentally investigated non-linear wave
resonance between surface and internal waves [2]. They managed to find out
theoretically and to study experimentally conditions of originating of a wave
resonance. These conditions, fair both for surface, and for internal waves,
were following [2].
Here 
-wave vectors and
frequencies of two interacting wave motions; 
- wave vectors and frequencies of synchronous
resonant waves. The classic methods of analysis of interaction between the
bodies moving in a heavy liquid, with
wave systems arising on the free surface, grounded on a linear theory of
sources, were designed at the end of past century and intensively developed
down to last time, in particular, with reference to research of ship waves [3]
- [6]. The theoretically and experimental investigation of waves which are
generated by the motion of a ship at values of Froude numbers
, (where - 
is the length of a ship), close to 0.5, has
allowed to find out an interference pattern of interplay of ship shear waves,
when the bow wave boosts the aft one and the wave drag of a vessel grows. Thus
half of length of a shear wave created by a driving vessel, appears to be equal
to the length of a ship. However this phenomenon was not esteemed as resonant.
Its description was executed with the linear theory, which results don’t show
the resonant interaction. In this case it was possible to speak about a
favorable or unfavorable interference of linear waves, as any padding
strengthening of intensity of sources modeling
a ship in linear theory was not received..
The picture
essentially varies at motion near to a free surface or gliding lifting body. Statement
and general solution of such problem were executed in a series of classic
works, in particular of N. E. Kotchin [5], M. V. Keldysh and M. A. Lavrentjev
[7] and L. I. Sedov [8]. In spite of a linearization of a problem in relation
to surface waves, created by the wing, the obtaining of the unambiguous
solution of a problem without padding allowances appears impossible. For its
solution the registration of a padding non-linear condition on a wing surface -
finiteness of speed in region of an sharp trailing edge is entered. This
boundary condition, saving linear dependence from an angle of attack, results
to a non-linear feedback between circulation on a wing surface and wave system
which is generating at its motion near to a free surface of a liquid.
The numerical
calculations of hydrodynamic parameters of foils were executed by the different
authors originally only for rather great values of submersions of a wing and
limiting cases of large or very small values of a chord-Froude number of a wing
[9-12]. It was connected with practical
requirements – hydrofoil crafts have the main regime of motion corresponding to
large values of a Froude number. Besides the attempts of fulfillment of
calculations at small submersions and arbitrary values of Froude numbers were
connected with considerable mathematical difficulties, bound with necessity of
calculus of composite wave integrals and solution of singular integral
equations of a wing theory. The part of these difficulties was overcoming at
the end of fiftieth- by the beginning of
the sixtieth years, when by T. Nishiyama [13], Isai [14], ,A. N. Panchenkov
[15] A. B. Lukashevich [16],], etc. in addition to the results of M.V. Keldysh and M. A. Lavrentyev [7] the
separate calculations of hydrodynamic parameters of a wing driving near to a
surface of a powerful liquid were executed. The generalizing of these results
was shown in the monographs [15,16].
However, the
calculations of hydrodynamic parameters of a foil in all range of Froude
numbers and relative depths of submersion
were not fulfilled. Only at the end of 70-th, begining of the 80-th years the similar calculations
were executed in USA [17] in the process
of working out of numerical methods of the solution of non-linear wave
problems.
In 1982
author with Ju. I.Faddeev organized
conference "Hydrodynamics of a wings driving near to a free surface
of a liquid, and planing surfaces ". M. A .Basin [18], A. Ja. Tkatch [19],
M. A. Makaseev [20], M. V . Lotfullin [21], A.N. Lordkipanidze [22] reported
about new results of calculations of hydrodynamic parameters of a wing driving
near to a free surface of a heavy liquid. The results of these investigations
showed the existence of a range of values of Froude numbers and relative depths
of submersion where is observing the abnormal behavior of hydrodynamic
parameters of the hydrofoil. Further M. A. Basin, A. N. Lordkipanidze and A.
Ja. Tkatch [23-30], improving the computational schemes with usage of the
quadrature formulas of Korneytchuk - Mishkevich - Gur-Milner [31-33] have
fulfilled the systematic computations within the framework of a linear theory
for influencing of a Froude number, relative depth of submersion, form and
thickness of the profile, and also relative length of a wing on its integral
and distributed hydrodynamic parameters by motion near to a free surface of
water. Later similar calculations under the linear and non-linear theory were
fulfilled by M. V. Lotfullin, S. I. Filippov, V. G. Stchigunov [34-35]. As have
shown the results of calculations for the wing with infinite length, by nearing
of a wing to a free surface of water, since 
, at definite for each of relative depths of submersion chord - Froude
number of a wing, which decreases at reduction of a diving depth, the intensive
growth of a derivative
(where 
- lift coefficient of a wing, 
- lift of a wing, 
- density of a liquid, 
- wing area projection) is observed. So, for example, at relative depth
of submersion 
= 0.2 and value of a chord-Froude number
the linear theory forecasts approximately
tenfold growth of . With decreasing of relative depth of submersion the theoretically meaning of the curve () is sharply increasing and even aims to
infinity at 
. It is interesting that the relation from a combined Froude number
formed on the area of a liquid above a hydrofoil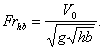 
The position of a
maximum of 
at almost all values
practically does not change and corresponds to
value of a Froude number
. At value 
the depth of submersion practically does not influence
on the hydrofoils lift (all curves of
relation as a function from 
are intercepted practically in one point at value =6.3). Decreasing of hydrofoils
relative length results in reduction of resonant maximum values,
however, the values of Froude numbers, corresponding to the resonance regime,
practically do not change.
With decreasing of
a relative depth of submersion the resonant value of 
is increasing and aims to 1 for
very small relative depths. In this limiting case the wing plays a role of
bottom and the resonant values of a Froude number come nearer to critical
values of this parameter on a shallow water.
The similar
resonant changes of lift effect were found out at calculations of relation of a
angle of zero lift spotted by curvature of the profile, from a Froude number
and relative depth of submersion. If in range of Froude numbers 
from unit to
infinitum for a hydrofoil with thin section as an arc of a circle the angle of
zero lift practically does not vary and has negative value, approximately equal
in radians
, where 
- the maximum relative arrow of
profile, then in range of Froude numbers from 0.4 up to 0.8 is watched sharp
growth of angle of zero lift, which one at 
becomes positive. The theory,
thus, forecasts paradoxical result. For a hydrofoil with thin section in the
form of circular arc, owes at è 
to arise not lifting, as usually, but
considerable drowning force.
The linear theory
forecasts even more exotic resonant effect for wings with a profile having
finite thickness. For these wings in a
resonant regime also must change the
angle of zero lift , which one at minor increase of a Froude number does a
zigzag jump from large negative value up to even greater (approximately in 2
times) positive value.
These
theoretically results at first, should
receive the applicable physical explanation, and, in second, required
experimental check. Though the having been available separate experimental data
[16], [17] qualitatively confirmed existence of abnormal effects, however,
before fulfillment of calculations the systematic experimental investigations
of this regime were not conducted.
With the purpose of
searching theoretically explanation of the obtained data the calculations of
distribution of pressure on a wing surface in this mode were executed and the
padding subroutines of calculation of deformation of a free surface of water
near to a wing are created. These calculations have shown, that main criteria,
determining a condition of maximum idealized value of , is the coincidence of a definite part of length of an attendant wave,
reshaped on a free surface, with a chord of a wing. However, as against a case
of a symmetrical picture of ship motion, this effect already with the full
foundation may be called resonant, while the amplification of a wave pattern,
in turn, can multiply circulation
current about a wing. If to count, that the considered resonant regime has the
wave nature, expedient it seemed to enter some analogy to a non-linear wave
resonance.
Created by the author
new classifications of waves, vortical and mushroom patterns, and also
transport-information systems [27,28, 38, 39, 68, 69,70] has allowed him to
esteem motion of a solid body in a liquid as the special form of a non-linear
surface solitary wave, which speed is equal to the running speed of a body.
Main geometrical parameter of this nonlinear wave is the size of a body in a
direction of motion. The main feature of a considered nonlinear wave is, that
near to boundary of a solid alongside with
speed and pressure fields forms the field of the area of a vorticity,
which is generating in a thin boundary layer near to a wing, is reshaped also.
On boundary of a
moving solid body always are available, as a minimum, two so-called
"stagnation points" (or points of change of the sign of a vorticity).
In these points, near to which one the speed of a liquid in the area without
vorticity is close to a running speed of a body (wave velocity), the appearance
of instability of vortex motion is possible. Near to these zones there is a
condition for originating of double helical vortexes ("vortical shockwaves
of the first kind ). Firstly the mathematical description of originating of a
similar kind of waves on the boundary of a liquid was given by M.A.Basin and
N.Ju.Zavadovsky in the work [40], where was established the analogy between
formation of a double helical vortex on boundary of potential flow of a liquid
and shockwave, that was a reason of
introduction for the detected phenomenon of a title - " vortical shockwaves
of the first kind". Due to diffusion of a vorticity the helical vortexes
are transformed into concentrated vortical patterns - vortical bubbles. The
formation of vortical bubbles characterizes originating particular, not
investigated earlier explicitly form of energy loss in wiscous liquid, bound
with interplay of a convection and diffusions of a vorticity inside a vortical
bubble. In case of unsymmetrical flow around a wing the formation of a vortical bubble near to an sharp trailing
edge on a suction surface of a wing results, due to non-linear interplay with
the main flow, in appearance of new layers of division-vortex sheets
("vortical shockwaves of the second kind "). They arise due to
sticking of vortical boundary layers from pressure and sucking surfaces of the
wing.
As a
result of sticking there is a separation of a vortical bubble from a body and
formation of new vortical pattern called by us " as vortical neutral
mushroom pattern ". It consists from an affixed vortical wave, driving
together with a wing; separated from it starting vortex (vortical scockwave of
the first kind) and thin vortex wake, connecting them, (vortical wave of the
second kind) in a two-dimesional case. At flow near the wing of final span the
vortex wake is skirted by permanently reshaped tip concentrated vortical
bubbles .As a result of this process in coordinate system, bound with a wing,
forms flow with circulation, determining from a condition of Chaplygin –
Jukovsky - Kutta on the trailing edge.
The set up above
scheme is utilized by the author together with I. G. Shaposhnikov for working
out of non-linear model of non-steady flow about the wing within the framework
of a frictionless liquid [41].
Earlier one of
founders of a wing theory - Lanchester [42-44] proceeded from similar wave
submissions about formation of circulation on a wing surface. However, further,
due to successes reached in the local analysis of the characteristics of wings,
grounded on a hypothesis Chaplygin – Jukovsky - Kutta [45-48] to the wave flow pattern of a wing
was given a little attention.
Flow pattern becomes considerably more complicated at motion of a wing near to
a free surface of a liquid, which is a new, padding source of wave motions.
Usually gravity waves are small and for their analysis is enough the applying
of a linear theory results. However, at increase of amplitude and energy of
gravity waves in region of their ridges the vortex motion is intensified and
the local speed in this zone becomes close to speed of wave motion. Limiting
theoretically possible stationary gravity wave on a deep water is the wave of
Stokes with 
(
- wave height, 
- its length), in top of which, the
stagnation point will be arised, the speed of a liquid in which is equal to a
wave velocity. The further increase of energy of a gravitational surface wave
results in appearance in its top of supercritical speeds and formation of
vortical shockwaves [49-53].
The destruction of
non-linear gravitational surface waves becomes in many respects equivalent to
the development of vortical shockwaves at asymmetrical circulating flow around
a body. Thus, vortex flow around a body with formation on its surface of
circulation current and flow, created by gravity waves, arising on a surface of
a liquid, bound can be esteemed from unified positions as non-linear waves,
connected with deformation or motion of demarcations of environments. The
indicated approach has allowed to identify a solid body, streamlined by a fluid
flow, with the solitary surface wave, which speed 
is equal to the speed of motion, and length is
proportional to length of a body,
;
Then it is possible
to define approximately the frequency and wave vector to of a vortical wave,
equivalent to driving wing : wave vector-
, frequency
. After such
identification it is easy to determine beforehand, not deciding previously
problem, range of Froude numbers, at which it is possible to expect resonant
interaction.
The parameters of
free waves in a heavy liquid of infinite depth, are connected by known
expressions 
As a condition of
appearance of vortex - wave resonance at steady motion of a wing we shall consider
equality of speeds of a body and affixed gravity wave, and also
commensurability of an affixed wave in
region of a body with its length (length of a body should make a definite part
of an affixed surge, approximately from 0.5 up to 1). Equating running speeds
and lengths of waves of a moving body and free gravity wave in a liquid, we
receive an approximated condition of originating a non-linear vortex - wave
resonance
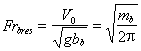
If to take into
account, that the value 
should vary within the limits from 1.0 up to 2.0, may be received: 
. Just in this
range of Froude numbers the main resonant phenomena are watched at motion of a
wing in range of relative depths
. At smaller values
of relative depths
the wing, being the source of disturbances,
simultaneously starts to play a role of local bottom, arranged on a shallow
depth under a free surface of water. In this case nature of surface waves,
their behavior near to a wing become all closer to behavior of waves on a
limiting shallow water, the speed which one in a limit corresponds to value
, where 
- depth of water, in this case - depth of wings submersion. For this
reason with decreasing of a depth submersion occurs the decreasing of resonant
value of a chord-Froude number of a wing and increase with aiming to unit of
resonant value of a Froude number on depth.
The worked out by
the writer concept of non-linear vortical shockwaves allows to estimate also, in what cases and
for what reasons the linear theory can give outcomes, distinct from outcomes of
experimental data, and also to forecast types of patterns, which may be formed
as a result of resonant interaction. So, for example, linear theory
calculations showed that the height of aft
wave may be much higher as by
limiting shock wave. Such wave is unstable and on its top must be formed the
concentrated vortex (or cascade of
concentrated vortexes), which diameter at relative depths, smaller then 
, is commensurable
with a depth of wings submersion. How
follows from the analysis of formation of vortical shockwaves on a wing, the
circulation can much considerably change only then, when the vortex, formed near
to a trailing edge, descends from a wing surface. In a resonant regime there is a mutual
amplification of growth of circulation and of a aft wave near the wing. The
destruction of the aft wave on a surface of water should result to that fact
that the concentrated vortexes which are generating near to a trailing edge of
a wing, can not separate from an edge, and the growth of circulation, and also
energy of a wave reshaped behind a wing, will be stopped. Thus, the
non-linearity at a vortex - wave resonance should result in to that the very large values of , obtained on the basis of a linear theory at small relative depths of
submersion, should not be realized. Thus outcome of non-linear interplay can
appear new vortical pattern reshaped near to a trailing edge of a wing,
including as members a vortical shockwave reshaped on a free surface of water
and a trailing vortex, arising near to a trailing edge of a hydrofoil.
The concept of
non-linear vortical waves and defined on its basis conditions of vortex - wave resonance appearance allow to
forecast values of foils speeds
applicable to a resonant flow regime of a wing and in an inhomogeneous
heavy liquid (or gas).
For this purpose
was found in litrature [50] the
dispersion relation of own wave
disturbances for the stratified liquid :
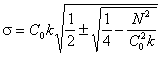, (1)
where
, 
- equilibrium
distribution of density for the altitude 
being a
continuously decreasing function of an altitude, 
- speed of sound of
non-perturbed flow at pressure
and distribation of density (is equal to relation of increment of pressure to
increment of density at a constant entropy); 
-
projection of a wave vector 
to 
axis. A resonance condition, as well as earlier has the form 
At large values of 
take place two strongly distinguished from
each other frequencies:
(2)
In the first case a
wave velocity is and at low speeds
of motion of the body sound waves attendant to body, are not present. In the
case of the bodies motion with the velocities, near to ,apparently, at the expense of non-linearity
of a flow pattern the minor dispersion of sound waves and appearance of
the vortex - wave resonance is possible.
However some information on existence of such regime to us is not known.
In the second case
the resonance condition results in a ratio
(3).
From a condition
(3) follows the conclusion: the speed of a body corresponding to resonant flow
about the wing, decreases up to zero point at
. This predicted
theoretically result may have the same principled value, as well as phenomenon
a vortex - wave resonance. Pursuant to it with decreasing of a degree of
liquids non-uniformity the resonant speed of wings motion aims to zero point. A
vortex-wave resonance is theoretically possible even at very small
heterogeneity’s of continuum and low speeds of bodies motion.
With the purpose of
check of this principled theoretically conclusion within the framework of a
linear theory the solution of a problem on motion of a wing near to a
demarcation of environments of different densities was reviewed and the
calculations of a lift distribution and integrated lift of a wing are executed
at different values 
and relative
depths. For this case the dispersion ratio is determined by the formula
(4)
And the critical Froude
number lies in range
,where 
(5)
The ratio (5),
though differs from (3), however characterizes the same tendency decreasing of
a resonance Froude number with reduction of a degree of a non-uniformity of
liquid (or gas).
The results of executed calculations have confirmed a
prediction for decreasing of resonant values of a Froude number to zero point at reduction of a degree of a non-uniformity of continuum .
. Last years by the
writer together with N.V. Kornev was worked out
the new vortical method of the solution of three-dimensional
Navier-Stokes equations, usage of which one, for our mind, will allow to explain in the future the
details of this interesting and
composite physical phenomenon. [54] - [63]
EXPERIMENTAL
RESULTS
There were
conducted in towing and cavitation tanks the tests of a hydrofoil having
rectangular plane form with relative length 
(
- wing span) with
flat –circular segment profile of a longitudinal section (thickness ratio
) in a broad region
of relative depths of submersion and Froude numbers [23-26], [28-30]. The tests were fulfilled at the region of
angles of attack
. The special attention was given to measurement of hydrodynamic
parameters and visualization of a flow pattern in resonant range of Froude
numbers and relative depths of submersion.
As well as was predicted theoretically, the considerable negative values
of lift of a wing were obtained even at positive geometrical angles of attack.
At 
and
were received the values
As it was predicted on the base of the concept
of vortical shockwaves, experimental data for 
in relation with the resonant values obtained on a linear theory,
on the contrary, were strongly delivered: experimental data appeared
considerably less then computational results. Besides the analysis of executed
photos has confirmed theoretically conclusions about formation in the indicated
range of Froude numbers and relative depths of submersion at all investigated
angles of attack above a trailing edge of a wing of a breaking up wave with a
vortical nozzle. At small angles of attack was observed a nose breaking up wave
of another shape- having flat top, boarded by non-steady
"beach-comber" The bow wave
decreases with increase of an angle of attack and at 
practically fades.
The tendency to disappearance of a bow wave with increase of an angle of attack
is confirmed by outcomes of
theoretically calculations. Outside of the resonant range of Froude numbers at
, as well as is
forecast by calculations, there is a quality change of a flow pattern. The top
of a aft wave displaces back and practically bow wave at once disappears. With
deleting from a wing of affixed aft the value of 
is increasing sharply. The meaning of
passes through zero point and with
further increase of speed receives positive values (if
). The flow near to
a wing becomes smoothly form with small wave deformations on a surface of a
liquid. The measured values of hydrofoils lift practically coincide the data
obtained with the linear theory. The analysis of experimental data has shown,
that outside of a zone a vortex - wave resonance the predictions of a linear
theory agree with experimental data. The predictions for a divergence of values
between results of
a linear theory and experiment grounded on the concept of vortical shockwaves,
were qualitatively confirmed. The experiment has shown also existence of new,
not studied before a collapse form of a non-linear bow wave. The range of
Froude numbers and relative depths of
submersion applicable to originating of abnormal hydrodynamic phenomena
in experiment practically completely has coincided with the theoretically
forecast range. That once again has confirmed main positions on which one the theoretically analysis was plotted.
THE
CONCLUSION
The detected
phenomenon of a vortex - wave resonance can find analogies not only in
hydrodynamics of bodies motion in an inhomogeneous liquid or gas, but also in
all those cases, when any rigid or deformed system is displaced in a nonuniform
medium. Such phenomena can be watched in
a meteorology, oceanology, astrophysics, plasma physics, chemistry, biology,
different manufacturing processes.
The designed theory
and presented concept allow to forecast conditions, at which it is necessary to
search similar phenomena. Such condition is the presence of a rigid or deformed
body migrating by rather inhomogeneous continuum, in which arising of
dispersing waves is possible. For the prediction of conditions of resonant
interaction it is enough to know the main dimensions of a body and basic
dispersion relations for free wave arising in the medium. The phenomenon of vortex - wave
resonance can arise and in homogeneous
medium, if during motion in this medium for whatever reasons there can
arise the phase changes.
So, phenomenon,
which can be referred to a vortex - wave
resonance, are detected by us at cavitation flow near the bodies in a
transient regime, when length of a cavity is close to a chord of a wing [16],
[64-66, 69], separated flow past of bodies [67], and another processes.
Coming from foregoing, it is possible to expect that
appearance of resonances of this sort is possible under different natural
phenomenas, in which is present a unhomogenious utter ambience (field) and
moving in it objects or vortex structures, and even to predict the conditions
of their origin.
Predicted theoretically and discovered experimentally
phenomena of nonlinear vortex-wave resonance contributes fundamental changes in
existing beliefs about the behaviour of currents near the bodies, moving in the
unhomogenious utter ambience. Knowledge of its nature and main criterions of
origin allows to predict theoretically, to find experimental and explain not
explored earlier anomalous regimes of the bodies motions in liquids, gas and other continuous
ambiences.
Opening of this phenomena stimulated a creation and
development of new methods of theoretical and experimental investigations of
vortex motions in hydrodynamics of ship
and other areas of science and technology , in connected with need of nonlinear
phenomena study by arising of vortex and wave motions of continuous media.
Concept of vortex shock waves of first and second
type, developed in connection with studying of the opened phenomena, and
identification of field of velocities near moving bodies and connected with
them traces and cavities with specific soliton nonlinear waves is using at
present for the explanation of known, but not studied before the end nonlinear
phenomenas, according with motion of bodies in liquids: separating of flow from
the bodies, origin and development of
circulation currents near the bodies ,
origin and development of destroying shock waves on the free surface ,
phenomenas, connected with cavitation of vortexes, flows near the interceptors
and holes, study of breakout of air to
the hydrofoils.
Discovered phenomena a curl-wave resonance can find analogies
not only in hydrodynamics of bodies, moving in the unhomogenious liquid and
gas, as well as in all that cases, when some hard or deformed system moves in
the unomogenious ambience. Such phenomenas are to be observe in metrology,
oceanology, astrophysics, physics of plasma, chemistry , biology , different
technological processes. Developping theory allows to predict a main condition,
under which follows to search the similar phenomenas.
Such condition is presence of any structure, moving in
the unhomogenious utter ambience (field), in which is possible the origin of
dispersive nonlinear waves. For the prediction of conditions of resonance
interaction is sufficiently to know main
gabarit sizes of structure and main dispersion correlation for free waves,
appearing in the ambience.
Phenomena of vortex-wave resonance can
appear and in the uniform ambience , if in the process of motion in this
ambience on one or another reasons are to occur phase transitions (for
instance, cavitation).
Emphases deserves that discovered when studying of the
flow near the nonsymmetrical bodies
theoretical result, that when reducing degrees of unhomoenity of
ambience resonance phenomena, nearly not fading, move in the area very small
relative velocities of moving bodies. This allows to use an open phenomena as
an efficient indicator of small unhomogenities in the ambience and device of
management, since at the resonance significant effect can be reached without
significant expenseses of energy.
Significance of received results consists not only in
discovering and studying of new unknown
earlier class of resonanse processes and vortex-wave structures, but as well as
in that , that developping theory allows to predict and find unknown earlier
forms of vortex -wave interaction , create artificially conditions for arising
this phenomena aplicable to practical problems, as well as create new ways and
develop new designs, part from which is already use at present in shipbuilding,
which are to find an using also in other areas of technology and scientific
studies.
Broad field of activity is opened for studying the
physical phenomenas also and vortex-wave structures, which can be formed at the
interaction of resonanse flow with other types of wave processes, vortex
structures and information-transport systems.
Vortex-wave resonance is one of the main mechanisms of
origin and stabilizations of new structures - that is to say one of the reasons
a structure- and systemforming, for biological objects particularly. So
condition of its origin and processes, occur during this type of occasions have
a particular interest for qualitative categorizations of fundamental processes
in the nature. One of the possible hypothesises of origin lifes on the World is
resonance interaction of solenoidal electro-magnetic structure of genome with
muschroom structure of the cell
Great role may
play the using of vortex-wave resonance for the artifical recognition of
images.
REFERENCES
(1) Sretensky, L. N.
(1977), “The Theory of Wave Motions of a Liquid”. M.: “Nauka”. 811p.(in Russian)
(2) Phillips, O. M. (1981), “A wave
interaction - the evolution of idea”,
Journal of Fluid Mechanics. A Special Issue
celebrating the 25th anniversary of the Journal and
containing editorial reflections on development of fluid mechanics, vol. 106.
(3) Michell, J .H.
(1898), “The wave resistance of a ship”, Philosophical Magazine, Ser 5, London,
vol. 45, p.106-123.
(4) Havelock, T.H.(1909), “The wave-making
resistance of ships: a theoretical and practical analysis”, Proc. Royal Society
of London, Sect. A, London, vol.82, ¹ 554, p.276-300.
(5) Kotchin, N. E. (1937), “About the wave drag
and lift of submerged in a liquid bodies”, Transactions of conference on the
theory of a wave drag, M., “ZAGI”, p.65-134.(in Russian)
(6) (1985),“Handbook on a ship theory”, In three
volumes. Under edition of Ja. I. Voitkunsky, Leningrad,
"Sudostrojenie", (in Russian)
(7) Keldysh, M. V.,
Lavrentjev, M. A .(1937), “About motion of a wing under the surface of a heavy
liquid”, Transactions of conference on the theory of a wave drag, M.: “ZAGI”,
p.31-64.(in Russian).
(8) Sedov, L. I.
(1937), “Plane problem about the gliding on the surface of heavy liquid”,
Transactions of conference on the theory of a wave drag, M, “ZAGI”, p.7-30 (in
Russian)
(9) Blumin, V. I.,
Ivanov, L. A., Maseev, M. B. (1964),.” Transport Ships on hydrofoils”, M.,
“Transport”, 256 p. (in Russian)
(10)
Logvinovich, G.
V. (1969), “Hydrodynamics of flows with free boundaries”, Kiev: "Naukova
Dumka", 216 p.(in Russian)
(11)
Epshtein, L. A.
(1970), “Methods of the theory of dimensions and similarity in problems of
hydromechanics of vessels”, Leningrad., "Sudostojenie", 208 p. (in
Russian)
(12)
Egorov, I. T.,
Sokolov, V. T. (1971), “Hydrodynamics of fast Ships”, Leningrad,
"Sudostojenie", 424 p. (in Russian)
(13)
Nishiyama, T.
(1959-1960), “Lifting line theory of the submerged hydrofoil of finite span.”
Parts 1-4,. Journal of the American Society of Naval Engineers,. vol. 71-72.
(14)
.Isai, W.H. (1959/60), “To the theory of hydrofoil
motion near the free boundary of water” Ing Arch., vol. 27, 29. (in German)
(15)
. Panchenkov, A. N. (1965), “Hydrodynamics of
hydrofoil”, Kiev, "Naukova dumka”,
552 p.(in Russian)
(16)
. Basin, M. A., Shadrin, V. P. (1980), “Flow mechanics
of a wing near to a demarcation of environments”,. Leningrad, "Sudostrojenie", 304 p.(in Russian)
(17)
. Salvesen, N. (1981), “Five years of numerical naval
ship hydrodynamics at DINSPDC”, J. of Ship Research, vol.25, ¹ 4, p. 219-235.
(18)
Basin, M. A.
(1982), “About forces acting on the wing, driving near to a free surface of a
heavy liquid”, Report on conference: "Hydrodynamics of a wing driving near
to a free surface of a liquid, and planing surfaces ", Leningrad (in
Russian).
(19)
.Tkatch, A. Ja..(1982-1983), “About influence of
environments weightiness on hydrodynamic parameters of a lifting surface”, The
report on conference: "Hydrodynamics of a foil driving near to a free
surface of a liquid and planing surfaces", Transactions of Leningrad Shipbuilding Institute: “Problems
of hydrodynamics of a vessel”.p 76-82.(in Russian).
(20)
.Makaseev, M. A.(1982), “To the solution of a plane
problem of streamlining of a thin floppy profile under a surface of a heavy
liquid”. The report on conference: “Hydrodynamics of a foil driving near to a
free surface of a liquid and planing surfaces", Leningrad.(in Russian)
(21)
Lotfullin, M.
V. (1982), “Motion of a system of profiles under a free surface of a heavy
liquid”. The report on conference: "Hydrodynamics of a foil driving near
to a free surface of a liquid and planing surfaces" Leningrad.(in Russian)
(22)
Lodrkipanidze,
A. N. (1982) “Calculation of hydrodynamic parameters of a thin highly-aspect
wing and comparison of results of calculation with experimental data”, The report on conference:
"Hydrodynamics of a foil driving near to a free surface of a liquid and
planing surfaces." Leningrad (in Russian).
(23)
Basin, M. A.;
Lordkipanidze, A. N.; Tkatch, A. Ja. (1985), “Phenomenon of vortex- wave resonance at research of
hydrodynamic parameters of a foil driving near to a free surface of a heavy
liquid”, Works of “NTO SP”, Issue 414, Leningrad, "Sudostrojenie", p.
23-31. (in Russian)
(24)
Basin, M. A.,
Lordkipanidze, A. N., Tkatch, A. Ja. (1990), “The solution of a problem on
stationary motion of a lifting surface
near to a demarcation of media. A vortex - wave
resonance”, Transactions of “NTO SP”¹.1. Leningrad, p.115-127. (in
Russian).
(25)
. Basin, M. A., Lordkipanidze, A. N., Tkatch, A. Ja.
(1991), “Hydrodynamic parameters of a lifting complex driving near to a free
surface of a heavy liquid”, Transactions of a Seminar on boundary value
problems, Issue 26: “Aerodynamics of flows with unknown boundaries”, Kazan:
KSU. p. 29-59 (in Russian)
(26)
Basin, M.A.,
Lordkipanidze, A. N., Tkach, A. Ja. (1991), “Vortex-wave resonance in the
hydrodynamics of foil, moving near the interface of the different density
media”, “Waves and vortices in the ocean and their laboratory analogues”, The
Fifth Annual Workshop of the Commission on the Problems of the World Ocean. Vladivostok, September 23-29, p.15-16.
(27)
. Basin, M. A. (1992), ”A foundation of classification
of non-linear wave motions and vortical patterns. A phenomenon of vortex -
wave resonance at motion of asymmetrical
bodies in an inhomogeneous liquid”, Problems of hydromechanics in development
of ocean, Materials of conference on applied hydromechanics of Kiev “IGM ANU”
p.192-193.(in Russian)
(28)
. Basin, M. A. (1993), “Wave formation by the motion
of a surface ship hydrodynamic complex near the free boundary. Classification
of nonlinear waves. Wave-vortex resonance”. Proceedings of the VI Congress of
the IMAM. Edited by Peter A. Bogdanov, vol.II, 15-20
November , Varna,. Bulgaria
(29). Basin, M.
A.(1995), “Vortex-wave Resonance in Hydrofoil Hydrodynamics”, International
Symposium on Ship Hydrodynamics Devoted to 85-th Anniversary of Birthday of
Abram M. Basin (ISSH). St-Petersburg: May, p.399-407
(30). Basin, M. A.
(1998), “Vortex - wave resonance” ,
Synergetics and methods of science. Spb.: "Nauka", p.415-418.(in
Russian)
(31). Kornejtchuk,
A. A. (1964), “The quadrature formulas for singular integrals”, Numerical
methods of the differential and integral equations solution and quadrature
formulas, v.4, ¹ 4 p.64-74.
(32). Mishkevich,
V.G. (1980),“About design of the quadrature formulas for singular integrals ,
meeting in flow mechanics”. Problems of shipbuilding, A serial: "Designing
of vessels" 1980, ¹ 23, p.98-108 (in
Russian)
(33). (1983),
“Propellers. Modern computational methods”,. (Bavin V. F., Zavadovsky N. Ju.,
Levkovsky Ju. L., Mishkevich V.G, Leningrad: "Sudostrojenie”,1983.
236p.(in Russian)
(34). Lotfullin, M. V., Filippov S.I.
(1987), “Streamlining of a profile by a heavy
liquid near to demarcations of media”, Mechanics of engineering,
Thesises of the reports of II republican technological conferences. Section of
mechanics of a liquid, gas and plasma, Bregnev, p. 44. (in Russian)
(35). Stchigunov,
V.G. (1995), ”The solution of non-linear non-steady wave problems by a vortical
method”. Ph. thesis. SPb.: SPb SMTU.(in Russian).
(38). Basin, M. A.
(1993), ”A Wave formation by the motion of surface ship hydrodynamic complex
near the free boundary. Classification of nonlinear waves. Wave-vortex
resonance”, Papers of IMAM 93 Congress, Ed. by P.A. Bogdanov, vol. II. Varna,
Bulgaria, November 15-20. p.51-58.
(39). Basin, M. A.
(1998).,“Foundations of classification of non-linear wave motions, vortexes and
transport systems”, Synergetics and methods of science,. M.A.Basin –editor.
SPb.: "Nauka" p.95-131. (on Russian)
(40). Basin, M. A.,
Zavadovsky, N. Ju.. (1985), “Model of a double helical vortex as the limiting
form of a free surface of non-steady flow of ideal incompressible fluid” .Works
of a seminar on boundary value problems. ¹.22.. Kazan: KSU. (on Russian)
(41). Basin, M. A,
Shaposhnikov, I. G .(1989), “New model of non-steady flow about a wing in a
frictionless liquid”, Mathematical and physical simulation in hydrodynamics of
a vessel, Transactions of “NTO SP”, Issue 18, SPb: “Sudostrojenie”, p.27-38.
(42). Lanchester,
F.W.(1884), “Stability of an Aerodrome”, The report on the meeting of Bimingem
society, July 19.
(43). Lanchester,
F. W. (1907), “Aerodynamics”, London.
(44). (1937)
”Aerodynamics”, Under general edition of R.F. Durand,. vol. I. “ONTI-NKTP.
USSR”, 436 p.(in Russian)
(45). Joukovski, N.
E., (1897), ”About the optimal angle of a slope of the aeroplanes”, An
aerostation and research of atmosphere, ¹1. (in Russian)
(46). Kutta, W.
M.(1902), “Lift in the flow of liquid”, Aerodynamic reports with illustrations,
p.133. (in German)
(47). Joukovski, N.
E.(1905-1906) “About adjacent vortexes”. Was reported by the author in the
Moscow mathematical society (November 15 1905) and was printed out in
“Transactions of branch of physical sciences “OLE”,v. XIII, ¹.2, 1906. (in
Russian))
(48). Chaplygin, S.
A. (1910), “About pressure of a parallel-plane flow on blocking bodies”, Moscow
mathematical collection, ¹ 28. (in
Russian)
(49). Longue
–Higgins, M. S., Fox, M. J. H.(1977), Theory of the almost -highest wave. The
inner solution”, Journal of Fluid Mechanics, vol.80, ð.721-742.
(50). Lighthill,
J.(1978), “Waves in fluids”, Cambridge University Press, London - New York -
Melbourne.
(51).Yuen, H.C.,
Lake, B.M. (1982), “Non-linear dynamics of deep water gravity waves”, Advanced
and applied mechanics, Vol.22. Edited by Chia –Shun Yih, Academic press, New
York-London-Paris- San Diego-San Francisko – Sao Paulo - Sydney-Tokio- Toronto,
p.67-229
(52). Amromin,
E.L., Basin, M.A., BushkovskyV.A.(1990), “Two solutions of a spatial problem on
limiting waves on a surface of a heavy liquid”, Applied mathematics and
mechanics, vol.54. N1. (in Russian)
(53). Maklakov, D.
V. (1997),”Non-linear problems of hydrodynamics of potential flows with unknown
boundaries”. M.:”Janus-K”, 280p.(in Russian)
(54). Basin, M. A.
(1984), “About change of vector of a summar vorticity of continuum at motion in
it of a solid body and at motion it inside a solid vessel.”, “Proceedings of AN
of USSR”, Mechanics of a liquid and gas,
¹ 1(in Russian)
(55). Basin, M. A.
(1984), “Change of the moments of a vorticity field of a liquid at motion in it
of a solid body”, Perfecting of running, seaworthy and maneuvering capabilities
of vessels. Materials on exchange of experience, ¹ 400, Leningrad, "Sudoctrojenie",
p.49-54. (in Russian).
(56). Basin, M. A.
(1990), ”Âasic equations of vortex fluid
motion. Vortex-wave resonance”, IUTAM Symposium on Separated Flows and Jets,
Novosibirsk: USSR p.39-41; Springer - Verlag. Berlin -Heidelberg , (V. V.
Kozlov, A.V. Dulov editors), p.113-116.
(57). Basin, M.
A.(1993), Basic equations of vortex fluid motion. Selected Papers,. Vol.1,.
Applied Hydrodynamics, St-Petersburg. State Marine Technical University, p.
23-34.
(58).Basin, M. A.,
Kornev, N.V., Zacharov, A.B.(1993), “Approximation of three-dimensional vortex
fields”. Transactions of Central research institute of a maritime fleet, SPb,
.p.184-196. (in Russian).
(59). Basin, M. A.,
Kornev, N. V. (1994), “Field of vortitity approximation in unbounded media”,
“JTF of RAN”, November, SPb, p. 179-185. (on Russian).
(60). Basin, M. A.,
Kornev, N. V. (1994), “New Computational Method of Vortex Dynamics”, Report on
the Euromech Colloquium 315,. Nurnberg – Erlangen, Germany,. March.
(61). Basin, M.A.,
Kornev, N.V.(1994), ”Approximation of Vorticity Field in an Unbounded Volume”.
Tech. Phys. 39 (11) , American Institute of Physics. p.1184-1187.
(62). Basin, M.A.,
Kornev, N.V.(1995), “Vortex Methods in Hydrodynamics”, International Symposium
on Ship Hydrodynamics Devoted to 85-th Anniversary of Birthday of Abram M.
Basin (ISSH), .St-Petersburg, May, p.431-450
(63). Basin, M.A.,
Kornev, N.V.(1998), “Incorporation of the viscosity in the vortex mrthod”
ZAMM,78, Issue5, p 335-344. (in German)
(64). Egorov, I.
T., Sadovnikov, Ju. M., Isaev, I. I., Basin, M. A. (1971), “Artifical
cavitation”, Leningrad : “Sudostrojenie”, 284 p.(in Russian).
(65). Egorov, I.
T., Basin, M. A., Sadovnikov, Ju. M., Shallar, A. V. (1972),. “A technique of
experimental research of non-steady hydrodynamic parameters of cavitating hydrofoils”, Experimental hydrodynamics of a vessel.
Materials on exchange of experience, Issue190, .Leningrad:
"Sudostrojenie", p.94-100. (in Russian)
(66). Basin, M. A.,
Shaposhnikov, I. G., Zilist, L. P.(1994), “Problems, methods and results in
hydrofoil cavitation”, Proceedings of the Second International Symposium on
Cavitation. April ,Tokyo, Japan, p.99-105.
(67). Basin, M. A.,
Borisov, R. V., Greengoltz, A. I., Guseev, A. S. Kagan I. S.
(1986),“Theoretical and experimental determination of the forces of viscous
nature by the vibration of the bodies at the fluid”, Proceedings of XV Ubileum
Seminar on the Ship Hydrodynamics, Varna: Bulgaria.
(68) Basin M.
A(1999). "Vortex-Wave Resonance" . Proceedings of the First
International Conference on Vortex Methods, November 4-5,1999, Kobe,
Japan.Pp.303-310.
(69) Basin M.A.
(2002) "Computers.Vortexes.Resonanses. Wave Theory of Structures and
Systems Interaction. Part 2".SPb.:"Norma"..144p.(in Russian)
(70) Basin M.A.
(2002) "Information -wave Theory of Structures and Systems". Physics
of Consciousness and Life, Cjsmology and Astrophysics ¹¹1-3.(in Russian) .