Оглавление

 

 

 

Часть  II

Человечество. Синергетический анализ

 

 

Глава 4

Сопоставление математических моделей динамики человечества: от клетки - до популяции

 

 

 

1. Простейшая модель роста параметра целого человеческой популяции

 

 

Одними из главных свойств живых объектов являются их рост и размножение, тесно связанные между собой. Так, например, рост клеток в какой-то мере соответствует размножению органических веществ клетки, рост объёма популяции или рост организма соответствует серии процессов деления  клеток с последующим их ростом. Рост популяции организмов (рост массы вида) определяется последовательным размножением и ростом живых организмов.

Возможный рост биосферы определяется динамикой  видов, её населяющих.

Отсюда следует, что в живой природе существует не только иерархия объектов, но и иерархия процессов, в которых участвуют эти объекты.  Одновременно с этим, в живой природе, так же как и в неживой, параметром целого, то есть параметром (мерой), интегрально характеризующим биологический объект как целостную структуру или систему, является его масса, которая на каждом уровне иерархии может быть связана с числом элементов (квантов), входящих в этот объект как в обобщённую волну. Выбрав эту меру в качестве основной, мы можем попытаться связать между собой динамические процессы происходящие на различных уровнях биологической иерархии.

Простейшим  и наиболее универсальным способом установления подобной динамической связи между уровнями иерархии от клетки до биосферы является, на наш взгляд, установление связи между динамикой объектов, которые могут быть включены в иерархию квантов - обобщённых волн, то есть исследование общих закономерностей зависимости роста массы объектов, лежащих на различных уровнях иерархии, от времени.

Рассмoтрим  первоначально  три основных уровня иерархии

1)                  Популяция макромолекул -Клетка

2)                  Популяция клеток - Организм

3)                  Популяция организмов -Вид

Меду этими тремя основными уровнями иерархии существует  ряд промежуточных, к которым можно будет вернуться на следующем уровне рассмотрения.

К этому списку можно добавить сверху ещё один уровень.

4)                  Популяция видов - Биосфера..

 Именно на этом уровне можно понять случайность и необходимость появления человечества и его роль в развитии биосферы. 

Такой же уровень можно добавить и снизу

0)                  Популяция атомов - макромолекула.

Однако, на первом этапе анализа мы рассмотрим лишь три основные уровни иерархии. 

Проблеме математического описания процессов размножения живых объектов посвящено большое количество работ(см., например  [22]). При этом обычно используются два типа моделей.

1. Непрерывные, сводящиеся к дифференциальным уравнениям, сглаживающие, например, процессы размножения или более сложные процессы взаимодействия биологических объектов.

2. Дискретные, сводящиеся к цепочкам отображений, или в более сложных случаях к итерационным процессам.

Чтобы читателю был понятен ход наших мыслей, начнём с середины нашей иерархии (её центра). А именно, с неограниченного размножения популяции клеток.

Сначала остановимся на образном и словесном описании.

Каждая клетка организма или популяции проходит следующие стадии:

1.Рождение после размножения клетки предыдущего поколения.

2.Рост после рождения

3.Размножение.

Из этого  следует вывод:

Если массу тела клетки в момент размножения принять равной некоторой величине , то после деления клетки каждая новая клетка имеет массу, равную . Таким образом, масса клетки за время её существования растёт в два раза. При этом, по-видимому, на первом этапе  скорость роста велика и равна некоторой конечной величине , а затем, перед размножением, стремится к нулю. К рассмотрению описания динамики массы клетки мы вернёмся на следующем этапе, а сейчас на том же словесном уровне проследим за судьбой популяции.

Итак, начнём с одной клетки. Пусть в момент одна клетка (), имея массу , разделилась на две (). Через некоторый промежуток времени  в момент времени  каждая из клеток достигает зрелости. Суммарная масса обеих клеток становится равной  Предположим, что в этот момент обе клетки вновь синхронно делятся . Их становится четыре (). В момент времени  масса четырех появившихся ранее клеток станет равной . В этот момент четыре клетки синхронно делятся и их число становится равным … В момент времени  происходит очередное деление клеток. В этот момент , в то время, как число клеток становится равным . Таким образом, мы получаем две потенциально бесконечные последовательности

 

n

1

2

3

4

5

6

7

8

9

10

N

 

2

4

8

16

32

64

128

256

512

1024

. Тогда как  , в принципе, изменяется непрерывно (хотя мы пока не знаем, как), число клеток  изменяется дискретно.

Математически последовательность  может быть описана итерационными системами

.

Решением этой системы итераций, являющейся геометрической прогрессией, является выражение

 

Аналогичное соотношение может быть записано применительно к  

Решением системы итераций в данном случае является формула

.

 

 

 Модель цепочки линейных комплексных отображений [34] как обобщение модели простого размножения.

 

Полученный результат может быть легко обобщён математически.

В [18] показано, что при анализе динамических структур и систем можно ввести комплексную волновую функцию (вектор-матрицу), описывающую динамическую систему (структуру), реальная и мнимая части которой тем или иным образом связаны с мерой, характеризующей её фазовое пространство и вероятностными характеристиками бифуркационных событий, в которых структура участвует.

            Эти обстоятельства позволяют рассматривать в качестве математической основы для исследования структур, динамика которых описывается континуумом или счётным числом состояний, аналитические функции комплексного переменного от времени .

В соответствии с высказанной гипотезой на следующем шаге рассмотрения в качестве области определения комплексной меры, описывающей возможные совокупности состояний, в которых может находиться динамическая система, примем поле комплексных чисел .

Рассмотрим в качестве функции, формирующей динамику системы, линейную отображающую функцию

 ,                                          (4.1)

где - комплексные параметры.

Величина  характеризует смещение точки комплексной фазовой плоскости  на постоянную величину, а комплексный коэффициент =определяет растяжение (сжатие) плоскости  и поворот точки фазового пространства относительно начала координат на угол . В случае общего положения (если ) отображение является взаимно однозначным. Отображением, обратным данному, является отображение, определяемое функцией  

Если , то . При этом обратное отображение формально не определено и  может быть принято любым. Проанализируем этот случай как предел случая общего положения при .

Пусть

При любом конечном  , задаваясь  , получаем  некоторое конечное . Однако, если , то при любых конечных значениях  оказывается очень близко  к . И только, при   может принимать любые значения.. При  любая конечная точка области  отображается в точку . Если  комплексную плоскость дополнить точкой , (дополнить комплексную плоскость до сферы),. то эта точка отобразится во всю плоскость. Прямое отображение в пределе  становится многозначным (возникает сингулярная асимптотика). Аналогичная картина возникает и при рассмотрении обратного отображения. Точка   преобразуется во все множество точек плоскости. Тогда как вся остальная плоскость отображается в бесконечную точку. Асимптотика линейного отображения при   может быть при несколько ином определении сведена к описанию динамики  одной стационарной точки.  при всех . Однако, такой же реальный результат дает и другое представление линейной функции  

Отыщем стационарные точки отображения. Для каждого набора коэффициентов  имеем единственную стационарную точку.

                                              (4.2)

Само же линейное отображение представляет собой растяжение и поворот относительно этой точки.

Покажем это. Введём новую переменную

                                               (4.3)

Тогда

                                              (4.4)

В случае , 

В случае  центр поворота стремится к бесконечности и при конечных значениях  превращается в сдвиг относительно предыдущего состояния на величину . Фазовая траектория динамической системы превращается в серию точек на комплексной прямой  (-действительное число). Каждая точка может быть описана комплексной координатой .

Осуществим проверку линейной функции на существование цикла второго  порядка.

Это условие имеет вид

                                           (4.5)

или

                                           (4.6)

Если , то

                                                  (4.7)

Все стационарные точки одновременно являются точками цикла.

Подозрительной на возникновение цикла становится особый частный случай линейного отображения, соответствующий значению . Специально рассмотрим этот частный случай.

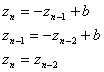                                    (4.8)

В случае  все точки плоскости  возвращаются на свои места. Циклическими оказываются все точки плоскости . Ведем новую переменную . Тогда получаем . Последнее отображение эквивалентно симметричному отображению относительно точки .  Для цикла третьего порядка имеем:

 

                               (4.9)

 

                                     (4.10)

 

Если ,  то  - По - иному выглядит картина, если . Корнями этого уравнения являются комплексные числа, представляющие корни кубичные из единицы.

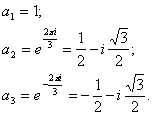                              (4.11)

В случае имеем, как и  ранее, сдвиг по прямой  и цикла третьего порядка не возникает. При других значениях  возникают циклы третьего порядка . При этом циклическими, как и ранее, становятся все точки плоскости . Приведённые два примера указывают на некоторую закономерность, которая может быть проанализирована методом математической индукции.

Предположим, что

.                           (4.12)

Доказать, что

                           (4.13)

Имеем

                                      (4.14)  

Подставляя (4.14) в формулу (4.13), получаем:

       (3.15)

Так как для первых двух значений -соотношение (4.13) справедливо, то оно справедливо для любых значений .

Попутно мы получили решение системы линейных итераций

.                                 (4.16)

Любая итерация линейной функции также является линейной функцией от начального значения переменной. Полученные соотношения позволяют в общем виде решить задачу о наличии циклов го порядка.

В общем случае условие цикличности принимает вид:

                                 (4.17)

Циклы го порядка формируются всеми отображениями, у которых

                             (4.18)

Тем самым устанавливается однозначное соответствие между особыми типами линейных отображений, формирующих циклы, при которых циклическими оказываются все точки комплексной плоскости, и циклическими системами с конечным числом допустимых состояний. Все точки комплексной плоскости  , лежащие на окружности радиуса 1 и имеющие вид , где   - целое число, формируют линейные отображения, порождающие циклы - ого порядка. Причём, циклическими оказываются все точки плоскости . Рассмотрим множество этих отображений более подробно. Вспомним соотношение . Далее рассмотрим класс аффинных отображений . Предположим, что . Эти отображения поворачивают плоскость  на угол . Если - рациональное число, то динамика соответствующего отображения порождает циклические повороты плоскости  с возвратом в каждой точки в старое состояние. Если - число иррациональное, то циклов не будет. Однако, с какой бы точки ни начался процесс итераций, динамическая система через некоторое время окажется сколь угодно близко от этой точки. Теперь можно перейти к рассмотрению более общего случая  В этом случае цепочка линейных комплексных отображений приводит  любое начальное состояние, обозначаемое нами , по спирали либо к , либо к .

В нашем случае простого размножения также может быть использована комплексная линейная итерационная система

.

 

 

Последняя формула, являясь частным случаем комплексного линейного отображения, одновременно совпадает с полученным  ранее итерационным соотношением. Наряду с дискретной моделью. может быть построена непрерывная действительная модель зависимости массы популяции клеток  от времени. При этом необходимо, однако, сделать некоторое допущение о характере изменения массы клетки в промежутке между делениями.

Наиболее простым и , по-видимому, наиболее естественным является допущение о том, что число  -является не целой, а действительной переменной, линейно зависящей от времени  .

Из соотношения , получаем

. Вместо   подставляем непрерывную переменную .

Тогда соотношение  

записывается в виде

 

Эта гладкая функция от времени обладает тем свойством, что масса популяции, гладко завися от времени, в моменты времени , где -целое число, точно совпадает с массой популяции в момент очередного деления.

Однако, такое представление никак не отражает ни дискретности процесса деления, которое представляется системой линейных отображений, ни реальных закономерностей изменения массы в промежутке между делениями, за исключением, пожалуй того, что эта зависимость, по-видимому, является гладкой  (но не обязательно дифференцируемой).

 Продифференцируем выражение по времени:

.

Мы получили линейное дифференциальное уравнение, эквивалентное в некоторые дискретные моменты времени, отличающиеся друг от друга на промежуток времени , рассмотренной выше системе итераций.

Величина  характеризует одновременно частоту размножения и величину коэффициента при времени в показателе экспоненты.

 

 

Комплексная модель непрерывной зависимости от времени.

 

Вернемся к полученному нами ранее решению линейной итерационной системы.. Считаем, что каждый шаг итераций соответствует некоторому постоянному промежутку внешнего времени.

Тогда , или, приняв , получим

,

где

                    

Эта непрерывная по  функция, которая при значениях  даёт все члены итеративного процесса, рассмотренного нами ранее, удовлетворяет линейному дифференциальному уравнению

 

                                               (4.21)

или

,                                               (4.22)

где

                                              (4.23)

 

Решение линейного дифференциального уравнения (4.23) даёт непрерывные фазовые траектории в виде спиралей в фазовой плоскости

Подробный анализ комплексной системы линейных уравнений приведён в [58 ].

Решение комплексного линейного дифференциального уравнения первого порядка также может служить моделью простого размножения. Для того, чтобы показать это, вернёмся к выражению 

.

 

Как и ранее, ведём непрерывное время таким образом, что через промежуток времени .

Отсюда  .

Считая, что последняя формула справедлива при любых действительных значениях входящих в неё величин, получим следующее модельное равенство .

Введя обозначения

,

где -промежуток времени между последовательными размножениями, получим

 

Это равенство, как следует из наших предыдущих рассуждений, является решением комплексного линейного дифференциального уравнения:

Рассмотрим теперь физическую интерпретацию этого уравнения в нашем случае

Будем считать, что модуль комплексного числа  характеризует число членов популяции  или некоторую интегральную меру популяции  в момент . Тогда формула  может быть переписана в виде

.

Эта формула эквивалентна рассмотренной нами формуле, соответствующей рассмотрению действительных переменных. Однако, наша формула содержит значительно больше информации, чем предыдущая. В ней присутствует ещё одна величина, которой раньше не было в дифференциальной записи, но которая существовала и была главной в дискретной модели размножения - а именно, .- частота размножения. Если , то величина - "выходит" из комплексной области, становится действительной величиной - наступает размножение.

Между размножениями её реальная часть может принимать различные значения от максимальных положительных до максимальных отрицательных. Пока мы не можем дать удовлетворительной физической интерпретации этому свойству модели, однако , возможно, что в некоторых случаях и это свойство может иметь физический смысл. Например, если размножающаяся структура является некоторой линейной или слабо нелинейной волной, или внутри неё происходят некоторые периодические процессы, лишь часть из которых выходит на поверхность. Возможно, эта величина характеризует некоторую информационную активность особи. В моменты перед размножением и после размножения эта активность максимальна -особь становится видимой внешнему наблюдателю. В промежутке между размножениями она отрицательна - наблюдается минимальная информационная активность - проявления деятельности особи минимальны.    

Последние рассуждения могут рассматриваться как гипотезы, требующие серьёзной проверки.

 

Однако обе указанные модели и основанные на них обобщения не описывают самого процесса простого размножения, интересуясь лишь его следствием - увеличением количества особей или какой то величины (типа массы), которая является мерой для каждой особи. При этом вообще не рассматривается механизм размножения, связанный (например) с делением клетки на две части и последующим ростом каждой из этих частей.

Ниже излагается впервые опубликованная в [18] новая базовая математическая модель, при определенных условиях сводимая к двум рассмотренным выше, но обладающая тем неоспоримым преимуществом, что в ней, без значительного усложнения математического аппарата возможно подробно проследить весь процесс размножения делением, включая деление каждой особи (клетки) и её последующий рост. Предложенная базовая модель обладает возможностями широкого обобщения, что позволяет надеяться на значительную перспективу её применения в различных приложениях, связанных с размножением особей различной природы, цепных реакций и ветвящихся процессов. Применительно к обсуждаемой нами проблеме модификация рассматриваемой модели может явиться базой для описания размножения клеток, составляющих организм отдельного человека. 

Предположим, что, каждая особь размножающейся популяции может быть представлена комплексным числом , модуль которого характеризует скалярную меру (главную обобщенную координату), соответствующую данной особи, а аргумент - отличие этой особи от других.

Рассмотрим в общем случае цепочку отображений

 

,                                               (4.24)

 

где -комплексное число. Подобная цепочка не только отображает одно состояние системы на другое, но и при каждом отображении порождает конечное или счетное число новых “особей”- значений многозначной функции- в зависимости от значения числа . Введя соответствующую замену переменных

 

 

и подставляя новую переменную в уравнение (4.24), получаем

 

                                       (4.25)

Здесь возникает проблема корректности перехода от второй части равенства к третьей. Не останавливаясь на ней подробно, примем, что многозначность функции, стоящей во втором члене, берет в третьем на себя функция , a для коэффициента выбираем лишь одну какую-либо ветвь степенной функции.

Подберем соотношение между  и  таким образом, чтобы коэффициенты в правой и левой частях уравнения (4.25) были равны. Расщепим задачу на две:

равенство

,

и уравнение

,

которое после опускания индексов принимает вид

 

                                                    (4.26)

 

Общее решение системы (4.26) может быть найдено в виде

 

                                   (4.27)

 

Как и прежде, можно перейти от дискретного рассмотрения к непрерывному, считая, что между  и  состояния меняются непрерывно во времени, через промежутки времени выполняется равенство (4.27).  Так же, как и ранее, формально вместо  равенства (4.27) получаем

,                                           (4.28)

где .

Рассмотрим теперь, решением какого дифференциального уравнения является функция . Для этого продифференцируем по времени левую и правую части уравнения

 

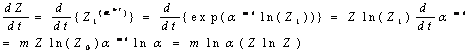
Степенным отображениям соответствует при уменьшении масштаба и переходу к непрерывности дифференциальное уравнение

                                                 (4.29)

Таким образом, нами установлено естественное соответствие между последовательностью комплексных степенных отображений (4.24) и комплексным дифференциальным уравнением (4.29).

Предположим, что в уравнениях (4.24)-(4.29) , где . - целое число. Тогда уравнение (4.26) может быть записано в виде

                                                         (4.30)

Если теперь принять, что модуль  равен единице, то преобразование (4.30) порождает из одной “особи” - , модули меры которых равны модулю меры -той особи, а аргументы отличаются. Таким образом -значная в данном случае степенная функция порождает на шаге размножение по  особей из каждой  -той особи. Тем самым уравнение (4.30), так же, как прежде частный случай уравнения (4.1), описывает размножение особей, однако, на наш взгляд, значительно более адекватно, так как значения комплексной функции действительно размножаются, при этом каждая “особь” - значение функции сохраняет свою индивидуальность (они различаются фазой).

Перейдем теперь к уравнению (4.27)

.                                               (4.31)

Если принять теперь, что  - размножение начинается с единичной особи, которой мы припишем реальную единичную меру, то на -том шаге мы получим -значений многозначной функции,  соответствующих числу значений .

При описании числа корней (числа значений многозначной функции) мы можем вновь воспользоваться соотношениями (4.1) и (4.2) при .

Наша модель допускает стандартную непрерывную аппроксимацию, аналогичную аппроксимации, примененной нами при получении формулы (4.3). Если, как и ранее, ввести представление о непрерывном времени, которое проходит между делениями особей, и предположить далее, что между последовательными делениями проходит время , равное , то размножение особей при больших значениях  может быть приближенно описано следующей модификацией соотношения (4.31)

 

                                               (4.32)

 

Однако, строго говоря , подобная запись дает нам очень мало нового, в отличие от подхода описываемого уравнениями (4.3-4.4), так как в действительности уравнение (4.1) реально описывает процесс размножения лишь  при значениях времени, . Именно при этих значениях параметра  число значений многозначной функции  становится равным числу членов размножающейся популяции, а каждое из чисел  описывает единичную особь.

При промежуточных значениях  формула (4.32) теряет физический смысл и, по-видимому, более предпочтительно пользоваться соотношениями (4.2-4.3), хотя и они неадекватно отражают реально происходящие при этом события.

В действительности после деления особи на  частей  каждая разделившаяся особь уже обладает мерой , модуль которой равен , а аргумент которой определяется номером деления и не меняется в процессе ее роста.

Возникает вопрос: а возможно ли модифицировать введённое нами описание таким образом, чтобы оно непрерывно описывало процесс роста особи в промежутке между делениями - то есть рост клетки. Оказывается возможно. Если предположить, что каждая вновь родившаяся особь имеет свое время, синхронизированное с общим временем, но начинающееся с момента её рождения, и при этом в процессе существования отдельной особи не реализуется потенциальная возможность перескока с одного состояния на другое, то рост особи уже со значительно большими основаниями может быть описан теперь уже однозначной функцией

, где .                                            (4.33)

Для того, чтобы увязать внутреннее решение с внешним, описываемым равенством (4.31), необходимо подставить вместо параметра его конкретные значения

.                                                    (4.34)

Введём для каждой особи масштаб внутреннего времени . Затем  введём в рассмотрение новую переменную . Тогда для описания роста особи получим следующее соотношение, в котором можно предполагать функции непрерывными и однозначными.

                                                 (4.35)

Ведём обозначение . Тогда формула (4.35) преобразуется к виду

Продифференцируем последнее соотношение по времени  , которое в нащем случае меняется от нуля до некоторого большого числа, стремящегося к бесконечности , если .

Этим соотношением, действительная ветвь которого удовлетворяет дифференциальному уравнению

 

                                               (4.36)

при начальном условии , представлена одна из возможных форм описания роста размножающейся особи..

При , при  .

Если  изменяется от 0 до , то  при постоянном значении  

Таким образом, наша модель описывает асимптотический рост характерной меры от до 1.

Общий оператор, описывающий размножение популяции приближенно может быть выражен в виде

 

                                         (4.37)

Здесь  - номер размножающейся особи .  С увеличением  число особей растет в геометрической прогрессии с показателем . Левый оператор в правой части выражения (3.14) представляет собой действительную функцию (аргумент комплексной функции равен 0). Правый оператор представляет собой комплексное число с модулем равным 1 и с аргументом  , величина которого равняется . Этот аргумент является паспортом каждой особи, отделяющим одну особь от другой на каждом шаге размножения.

Проанализируем полученное решение.

Пусть мы имеем . Тогда . Имеем всего одну особь, мера которой описывается следующим комплексным числом   . То есть первая особь начинает свое существование с меры . Откуда взялась эта первая особь - это вопрос философский . Однако, достоинство рассматриваемого нами описания состоит в том, что оно инвариантно относительно трансляции . Мы можем взять любую особь из любого шага формирования популяции, приписать ей значение  и умножив соответствующий ей правый оператор на комплексно-сопряженный вновь прийти к началу отсчета. Что, в принципе, соответствует реальности. Далее предположим, что  Тогда мера все той же особи будет описываться однозначной комплексной функцией . .

Эта функция является монотонно растущей функцией , которая при . стремится к 1. Здесь возникает некоторая неточность, на которую мы пока не будем обращать внимания, но которая потом, при более детальном рассмотрении, возможно,  будет играть существенную роль. В действительности модуль меры  при любых конечных значениях . Это отличие можно на первых порах считать малым и не влияющим на наши дальнейшие рассуждения. Однако . при большом числе размножений это расхождение может привести к вырождению популяции, то есть к постепенному уменьшению меры каждой особи. Это противоречие может быть преодолено, например путем введения некоторого поправочного коэффициента определяемого отношением  и стремящегося к единице при .

При  происходит размножение особи - деление ее на  дочерних, каждая из которых с этого момента начнет расти по тому же закону . по которому росла материнская особь..

Таким образом, после первого деления получаем различных особей, каждая из которых имеет свой индекс, определяемый аргументом характеризующей её переменной  и одинаковый для всех них модуль равный в начальный момент после размножения величине   или точнее, близкой к ней.

На следующем шаге все то же самое повторяется для каждой особи, однако при этом  в геометрической прогрессии растет их количество.

Предложенная модель может быть легко модифицирована и обобщена на различные типы ветвящихся процессов, каждая особь которых обладает двумя свойствами - роста и деления. При этом имеется три управляющих параметра(), которые могут изменяться на каждом шаге размножения, что делает предложенную модель чрезвычайно гибкой и приспособленной к модернизациям.

Необходимо отметить еще несколько особенностей рассмотренной модели.

В ее рамках легко можно проводить селекцию, исключая из дальнейшего размножения отдельные группы особей.

Необходимо также обратить внимание на то, что в предложенной модели рассматриваются степенные функции (пока с рациональными показателями степени)- при этом итерационный процесс для степенных функций при определенных условиях эквивалентен дифференциальному уравнению, в правой части которого стоит функция, часто встречающаяся в теории энтропии и информации.

Указанные особенности модели, по-видимому не являются случайными.

Специальное математическое исследование многозначных ( в частности, бесконечнозначных функций комплексного переменного, например , степенных и логарифмических, к которым мы пришли в данной работе, может дать мощный аппарат для исследования процессов, описывающих явления, будущее которых многозначно, то есть явления . в которых есть возможность выбирать варианты будущего поведения. Особо интересными могут оказаться процессы, описываемые степенными функциями с иррациональными показателями степени или логарифмическими функциями, где число возможных вариантов будущего бесконечно (счетно) и на каждом следующем шаге рассмотрения и необходимо вводить дополнительные условия (свободу воли) для выбора той или иной траектории динамической системы.

 

Благодарность.

Авторы благодарят Рэма Георгиевича Баранцева за помощь в написании настоящего параграфа  и новые идеи по дальнейшему развитию предложенной модели.

 

 

 

2.Возможные варианты развития предложенной математической модели

 

 

Как мы уже отмечали, человеческое общество представляет собой биологическую волну, элементом, квантом которой является человек. Наша теория уже настолько развита, что для простейшей биологической волны (типа размножающихся клеток) мы можем построить достаточно представительную модель ее неограниченного роста с учетом простого размножения и роста каждой особи (кванта). В интегральном смысле число квантов, входящих в такую волну, растет по экспоненциальному закону, удовлетворяющему линейному дифференциальному уравнению (4.4), решение которого соответствует экспоненциальному росту. При этом каждая особь совершает свой собственный обмен с внешней средой и кроме момента размножения, когда в одном месте рождаются две особи, которые затем расползаются, связь между ними отсутствовала. Такая волна может быть названа свободной биологической волной. Её реализация чаще всего происходит на поверхности Земли, то есть на двумерной поверхности или в толще воды, то есть в объеме. В этом случае каждой особи, кванту вида приходится выживать в одиночку и совершать обмен веществ, энергии и информации со своим участком поля. Никакой внутренней организации, кроме самого размножения, в этом идеальном случае не требуется. Каждая особь ведет себя самостоятельно и создаваемые различными особями внешние поля не синхронизируются. Весь контролирующий и управляющий механизм сидит внутри каждой особи. Если теперь предположить, что существует некий условный радиус внешнего поля, который достаточен для рационального взаимодействия с одиночной особью, то можно в первом приближении оценить форму и скорость движения такой биологической волны. В соответствии с решением, например, простейшего уравнения размножения

,

 имеем . Здесь  - число особей (квантов) в момент времени , - число особей (квантов) в момент времени =0.  - некоторый коэффициент , характеризующий скорость размножения особей, физический смысл которого мы сейчас выясним. Пусть время, через которое, в среднем, размножится (то есть разделится на две одна клетка), равно . Тогда, если в момент времени =0, было  особей, то в момент времени  их число увеличится вдвое. Отсюда получаем простое соотношение

.

Таким образом, величина  обратно пропорциональна среднему периоду размножения клеток . Введем еще один параметр, характеризующий нашу волну, среднюю площадь  (или объем ) поля, необходимый для существования биологической особи – (кванта). Тогда для свободного существования волны - вида достаточна площадь , (объем ). Если считать, что распространение вида происходит однородно по всем направлениям, то радиус  такой свободной биологической волны определяется из соотношения.  , (или ). Отсюда получаем зависимость радиуса свободной биологической волны от времени  (или - в случае объёма). Последние формулы можно несколько упростить. Положим =0. Тогда ().

Получим

().

Как следует из полученных формул, радиус волны прямо не зависит ни от того поля, которое нужно каждой особи , ни от числа особей. Эта зависимость связана лишь с первоначальным радиусом волны и скоростью размножения особей. Две первые величины скрыты в начальном радиусе расселения, если считать расселение в этот момент свободным.

Из последних формул можно также определить зависимость от времени скорости распространения простейшей биологической волны от времени.

 ()

Скорость перемещения волны размножения растет также по экспоненциальному закону, но показатель этого закона вдвое ( втрое) меньше , чем рост числа особей в популяции.

Все это справедливо для свободного роста популяции.

Если же такой рост по каким- либо причинам, например. в связи с естественной гибелью членов популяции невозможен, то рост числа её членов начинает уменьшаться и популяция выходит на некоторое равновесное состояние. Математика этого процесса очень хорошо разработана. Она может быть описана несколькими типами уравнений, один из типов уравнений такого рода – это знаменитое логистическое уравнение [25].

 При этом стационарное состояние, на которое выходит популяция, оказывается устойчивым в линейном приближении. В настоящее время теория логистического уравнения и системы итерационных уравнений Фернхюльста, соответствующая этому уравнению, подробно разработана.[11]. Аналогичный анализ устойчивости может быть сделан и для предложенного нами уравнения (3.15). Стабилизированные популяции могут существовать довольно долго, но это вовсе не значит, что они абсолютно устойчивы. Значительные дискретные возмущения могут ввести систему в циклическое состояние, а еще более значительные – привести систему в состояние хаоса.[23,24 ]

 

 

 

 

3. Переход к формированию многоклеточных организмов

 

 

Однако рассмотрение развития популяции на поверхности Земли и в пространстве позволяет наметить еще один качественный путь к развитию популяции в условиях ограниченности средств для питания. Этот путь и избрала Природа при создании многоклеточных животных и растений. Пусть пространство, в котором возможно использовать природные ресурсы для получения пищи, ограничено и отделено от другого аналогичного пространства значительной зоной, в которой получить пищу и энергию невозможно. Как поступает популяция в этом случае. Характерным эмпирическим примером является слизневик (Dictyostelium disciodeum) [26], который может существовать как в форме отдельных клеток, так и в форме единого организма. В фазе роста каждая отдельная клетка этого гриба существует как отдельная особь и их распространение по поверхности осуществляется по законам, изученным нами ранее: они экспоненциально размножаются и занимают все большую площадь. Однако, когда пищи начинает не хватать, система переходит в состояние самоорганизации. В чем оно состоит? Одна из клеток, расположенных в центре популяции, становится «пейсмекером», центром концентрации, испуская особые химические вещества, притягивающие к центру все остальные клетки (создавая новое биологическое поле). Формируется многоклеточная пространственная структура, клетки в которой расположены впритык друг к другу. Во-первых, вместо поверхности появляется объем, что уменьшает радиус популяции. Во-вторых, расстояние между клетками – членами популяции стремится к нулю. Они сближаются практически вплотную. Тем самым, внешней средой для внутренних клеток становятся только близлежащие клетки. Резко уменьшается поверхность соприкосновения популяции с внешней средой. Между клетками устанавливается «любовь». Каждую клетку кормят ее соседи. Существование каждой клетки обеспечивается существованием всех остальных. Практически нелинейная ударная волна превращается в резонансную грибовидную структуру. Биологические поля, создаваемые отдельными клетками, синхронизируются, формируя биологический диполь. Тем самым открывается пространство для дальнейшего роста биологической структуры. Однако, законы этого роста уже становятся совсем другими.

Об этом поговорим подробнее. Сближение внутренних клеток практически предотвращает их рост, а следовательно, и размножение (кстати, нечто подобное происходит в настоящее время с человечеством, переселяющимся в многоэтажные города и увеличивающим средний срок жизни).   Как нами будет показано ниже, тем самым увеличивается период дипольной волны, которую формируют размножающиеся клетки. Срок жизни каждой из них значительно увеличивается и становится сравнимым со сроком существования популяции в целом.  При этом, хотя несколько снижается обмен веществ каждой клетки, но не настолько сильно, так как ей необходимо осуществлять оптимальным образом свои жизненные функции. Фактически этот процесс во многом аналогичен процессу формирования городов, а также конденсации неорганического вещества.  Однако, механизм самоорганизации в этом случае оказывается значительно сложнее, чем в последнем случае.

Во первых, устанавливается существенное различие между клетками, находящимися на границе объема, и клетками, находящимися внутри. Граничные клетки обладают значительно большей свободой и становятся более активными. Так как изменения внешнего поля, вызываемые синхронизированной группой клеток, на порядок превышают поле, индуцированное той же группой свободно живущих клеток, то зона влияния такой грибовидной структуры оказывается значительно выше. Граничные клетки могут формировать длинные нити, связанные с основной грибовидной структурой, и расположенные по силовым линиям нового биологического поля (ножки грибов), и в новых местах рождать новые грибовидные структуры, связанные с первичными. Тем самым оптимальное разграничение обязанностей клеток и разделение их на внешние и внутренние позволяет виду строить два типа  связанных между собою поселений – концентрированные грибовидные структуры с плотным поселением клеток  и создающие мощное биологическое поле и нитевидные структуры, охватывающие большие поверхности, расположение которых соответствует распространению этого поля. Нитевидные структуры служат для активного добывания пищи, а также для транспортировки пищи к грибовидным структурам. Так многоклеточные биологические объекты вводят в своей структуре серьезную дифференциацию. Часть функций управляющего механизма от отдельной клетки передается всему многоклеточному организму.  Почти хаотическое движение клеток в свободной биологической волне, имеющее большое число практически равновероятных степеней свободы для каждой клетки, переводится при том же теоретическом числе степеней свободы в упорядоченное организованное движение системы, в которой движение каждой клетки синхронизировано с движением остальных. Возникает внешний по отношению к отдельным клеткам гомеостатический контроллер, проявляющийся в трансформациях биологического поля,  например, в синхронном электромагнитном взаимодействии отдельных клеток, или в появлении химических веществ, синхронизирующих поведение отдельных клеток (зачаток эндокринной системы). При этом, однако, происходит, обратное влияние вновь формирующихся полей на порождающий контроллер (геном) отдельных клеток. Этот обратный процесс должен носить значительно более длительный характер. По-видимому на геном действуют не короткодействующие и близлежащие поля, а длительно существующие изменения дальнего поля биологического объекта.

Наряду с этим происходит интенсивный информационный обмен с полем системы. Появляются специальные клетки, становящиеся зародышами диффузной  нервной системы.

Формирование многоклеточных структур явилось важнейшим шагом в развитии биосферы. (Хотя нам кажется допустимой также гипотеза о том, что в историческом масштабе многоклеточные организмы появились почти одновременно с одноклеточными). Появились новые, макроскопические кванты живой материи, существование которых позволило регулировать размножение и одновременно увеличить сферу действия живых организмов. Но главное, что произошло, это возник принципиально новый, внеклеточный механизм управления  совокупностями клеточных структур (гомеостатический контроллер), который привел к созданию новых целостностей – организмов. За счет ограничения степеней свободы отдельной клетки появились принципиально новые степени свободы на более высоком масштабном уровне, которые ранее были практически невероятны. Фактически управление частью микроскопических степеней свободы в вероятностных событиях клетки было делегированы наверх, нарождающемуся контроллеру новой структуры.

С макроскопическими событиями произошел несколько более сложный процесс. Те события , которые ранее были невероятны (то есть не могли или почти не могли произойти), но которые наиболее желательны в данном случае для выживания системы идентичных клеток, благодаря возникновению межклеточного полевого управляющего механизма становятся значительно более вероятными, чем все остальные, меняется сам набор наиболее вероятных событий и меняется структура вероятности макроскопического объекта. При этом число возможных макроскопических событий, соответствующих синхронному взаимодействию элементов системы, увеличивается. Если ввести понятия энтропии –информации макроскопических событий, то до объединения реально возможно было лишь одно макроскопическое событие, соответствующее максимуму энтропии микроскопических событий. Теперь, после самоорганизации, те макроскопические события, которые ранее были практически невероятны, приобрели статус событий, имеющих достаточно высокую степень вероятности. При этом число таких событий с развитием управляющего механизма растет за счет отбора все новых степеней свободы у элементов системы – отдельных клеток . Тем самым возрастает энтропия – информация, управляемая контроллером макроскопического объекта и возрастает эффективность межклеточного управляющего механизма. Возникает новая целостная структура способная к резонансному изъятию энтропии-информации из микромира.

Почему-то этот процесс для человека работает при соотношении структуры и ее элементов, равном 10**13?.

Энтропия может рассматриваться как иерархическая величина, зависящая от масштаба рассмотрения системы [3], [35], [58],[18], которая не только растёт при передаче энергии из макромира в микромир, стремясь к своему максимальному значению в соответствии со вторым законом термодинамики, но у живых организмов за счет формирования новых уровней иерархии передается из микромира в макромир. При этом формируются новые, невероятные ранее степени свободы за счет ограничения возможностей выбора каждого отдельного элемента. Здесь присутствует некий закон природы, дополняющий второй закон термодинамики, который сформулирован А.М. Хазеном в виде закона максимума роста производной от энтропии по времени.[58], и который для своей строгой формулировки требует более тщательного исследования проблемы синтеза новой информации в бифуркационных процессах.

После формирования многоклеточных структур возникает вопрос об их взаимодействии с окружающим полем и между собой. Нас в данном случае будет интересовать второй вопрос – вопрос о взаимодействии многоклеточных структур между собой. Первым вопросом является вопрос размножения. Простейшим и, по-видимому, первым реализовавшимся вариантом размножения многоклеточных структур, явился вариант размножения делением, аналогичный клеточному (современным аналогом такого размножения является вегетативное размножение ). Однако при таком типе размножения после отделения одной макроскопической структуры от другой возникает проблема связи и взаимодействия между структурами. Конечно, здесь может действовать тот же механизм, что и при межклеточном взаимодействии, сначала действует обычная свободная волна, способствующая расселению размножающихся организмов, но значительно большими шагами, чем это было ранее. А в случае ограничения в росте популяции – срабатывание механизма «коллективной любви- что-то вроде коммунизма» с формированием сверхорганизмов.

Хорошим примером такого механизма является жизнь кораллов. Однако , это не самый интересный вариант. Природа придумала нечто новенькое и значительно более интересное.

Это то же самое, что наряду с фотонами, природой созданы электроны и протоны, притягивающие друг друга значительно сильнее, чем просто гравитационное притяжение .

Наряду с видовой резонансной «любовью» она придумала половую любовь. Мы можем только догадываться о происхождении этой загадки мироздания – половой любви. Однако кое - какие догадки, может быть, совершенно фантастические, мы можем высказать.

ДНК в клетках закручены в двойные спирали. При размножении клетки происходит разделение спиралей и поле клетки вместо дипольного  может стать более сильным полем нескомпенсированной закрученной спирали.

Если в обычных клетках при размножении элементы ДНК находят себе пару (однако возможна и неполная компенсация, что может явиться причиной биологического сродства клеток, да и особей одного вида), то при размножении многоклеточных организмов могло произойти так, что первоначально наряду с разделением всего организма происходило и разделение части клеток на  не полностью сформировавшиеся, а имеющие лишь половинный набор генов.  . Эти клетки  внутри организма очень активны и каким либо образом перестраивали весь организм на поиск себе пары, то есть организма, в котором остались закрученные нескомпенсированные клетки с противоположной закруткой. Биологические поля таких организмов оказывались значительно более активными и притягивались друг к другу. Постепенно в таких организмах выработался внутренний механизм создания подобных не до конца разделившихся клеток, наличие которых резко увеличивает сродство - «любовь» организмов друг к другу. Этот механизм, по-видимому, является главным достижением контроллеров многоклеточных организмов, так как он качественно усилил сродство особей одного вида, создав половое влечение, которое оказалось сильнее любых других уз, связывающих организмы. Да и само понятие вида для высокоорганизованных  организмов определяется теперь способностью особей этого вида спариваться между собой. Изменились и возможности биологического развития. Увеличение числа  многоклеточных организмов с половым размножением ( в том числе и людей) стало подчиняться теперь совсем иному закону, о котором мы будем говорить несколько подробнее в следующем параграфе. Этот факт стал особенно важным именно теперь, когда человечество вступило в критическую фазу своего развития. Половое размножение, создавшее сильнейшее поле притяжения и разделившее всех особей данного вида, не зависимо от их предыдущей истории и нынешнего положения на две почти равные половины, сильнейшим образом , притягиваемые друг к другу, создало первые и возможно наиболее сильные структуры внутри видов, размножающихся половым путем.

 

 

 

 

4.Модель роста числа организмов,  размножающихся половым путем

 

 

При этом оказывается, что математика может оказать здесь неожиданную , но очень существенную помощь. Хотя, в действительности, процесс изменения числа живущих на Земле людей происходит дискретно, с рождением каждого человека число их увеличивается на единицу, а со смертью каждого из них уменьшается также на единицу, однако число людей настолько велико, велик и диапазон времени, в течение которого существует человечество, что процесс изменения числа людей  в первом приближении может считаться непрерывным.

Тем самым, изменения числа людей в соответствии с синергетическими принципами, может быть описано некоторым дифференциальным уравнением, общий вид которого

.

Так как человечество развивается, по-видимому, в основном, по своим внутренним законам, то изменение его параметра целого может описываться автономным уравнением, в котором является функцией только от . Уравнение динамики  параметра целого принимает вид

.

Конечно, на развитие человечества оказывают влияние различные факторы. Однако если человечество считать системой, развивающейся по единому закону, то этот закон должен быть связан с основным свойством человеческой популяции, а именно с половым характером размножения. В соответствии с половым характером размножения все люди делятся на две половины - мужчин и женщин,- при этом каждый мужчина  может в принципе, образовать пару с любой женщиной, и результатом этой пары может быть рождение ребенка. Естественно, такие возможности не осуществляются всегда, однако это можно учесть введением некоторого коэффициента. При таком наиболее естественном предположении вид функции  существенно упрощается и принимает вид. [25]:

 

,

а само дифференциальное уравнение получает форму

                                                 (4.38)

В монографии [10] дано иное обоснование целесообразности применения этого уравнения на довольно длительном интервале существования человеческой популяции.

“Отмеченный кооперативный  закон роста ( удовлетворяющий уравнению (4.38)) в значительной мере является прямым выражением информационной природы развития. Распространение и передача из поколения в поколение информации – знаний и технологий, обычаев и культуры, религии и, наконец, представлений науки есть то, что качественно отличает человека и человечество в своем развитии от животного мира. [28 ], [21 ], [29]. …

Такая зависимость возникает потому, что при обмене и распространении информации происходит умножение числа её` носителей в результате разветвленной цепной реакции. Обмен и распространение информации отличается от эквивалентного обмена ценностями, когда, например, при обмене невесты на стадо баранов общее число объектов обмена сохраняется. Разница удачно выражена в анекдоте о том, как хорошо обмениваться идеями: при этом каждый приобретает по идее, ничего не теряя. Очевидно, что распространение информации необратимо – слово не воробей, вылетит - не поймаешь! С другой стороны, обмен товарами принципиально обратим.

Сейчас принято выделять информационную составляющую современной цивилизации. Но следует подчеркнуть, что человечество всегда было информационным обществом. Иначе трудно понять природу квадратичного роста, так отличающего человека от остальных животных»

 (А существует ли это отличие? Ведь все известные нам виды многоклеточных животных, кроме домашних, либо уже стабилизировали свою численность, либо исчезают под влиянием человека. Так что не с чем сравнивать.).

В учебнике [25] В. И. Арнольд даёт другое объяснение квадратичной зависимости скорости изменения числа людей от времени, связанное с половым характером размножения .

Ешё одно объяснение квадратичной зависимости, позволяющее более глубоко проникнуть в сущность взаимодействия человечества с окружающей средой, даёт А.В. Подлазов [50]

"С.П. Капица, строя феноменологическую модель роста человечества, объясняет рост гипотетическим информационным взаимодействием, интенсивность которого пропорциональна числу парных отношений между людьми, что и приводит к квадратичному закону роста (2) [8,10].

      Согласно высказанным в работах [8,10] идеям, демографический переход происходит , когда прирост численности человечества за одно поколение становится сравнимым с числом уже живущих людей. Тогда информационное взаимодействие не успевает подстраиваться под столь стремительные изменения. Однако, как легко понять, при этом рост населения, если он действительно обусловлен информационным взаимодействием, должен вовсе не прекратиться (как это происходит в действительности) а лишь замедлиться , ведь уже установившееся информационное взаимодействие не исчезает.

Ранее нами был развит отличный подход , основанный на представлении о демографической роли взаимопомощи и о жизнесберегающих технологиях[59,60]. Поясним вкратце его суть.

             Изменение полной численности человечества может происходить лишь за счёт процессов рождения и смерти людей.

            Однако рождаемость не может быть источником роста населения, так как её уровень обыкновенно занижен по сравнению с предельными репродуктивными возможностями человека. Это позволяет избежать возникновения колебаний численности, обусловленных отставанием её изменений по отношению к изменениям доступных ресурсов.

            Поэтому в процессе своего развития человечество выработало множество социально-культурных и экономических ограничителей рождаемости . В зависимости от культуры и эпохи они принимали формы религиозного ограничения свободы сексуальных  отношений , установления возраста совершеннолетия, необходимости дать приданое за невестой или уплатить за неё калым, многожёнства, сексуальной революции, эмансипации женщин и т.п.

            Таким образом, единственным источником увеличения численности человечества служит уровень смертности. Он может быть уменьшен за счёт взаимопомощи, когда действия одних людей помогают выжить другим. В отличие от животных человек, будучи разумным, не ограничен коллективными схемами  коллективного поведения и может находить те формы взаимопомощи, которые наиболее эффективно используют имеющуюся численность. А уменьшение смертности должно приводить к росту численности, которая, в свою очередь, способствует дальнейшему уменьшению смертности, и т.д.

            Вместе с  тем, непосредственная взаимопомощь возможна только в небольших популяциях и не может быть фактором , значимым для глобального демографического процесса. Чтобы одни люди могли использовать для уменьшения смертности результаты деятельности других, необходимо какое-то взаимодействие между различными частям человечества.

            Однако, люди сегодня, как и миллион лет назад, живут весьма обособленно, занимаясь преимущественно своими делами и уделяя мало внимания внешнему миру. Иными словами, искомое взаимодействие должно быть очень мощным, чтобы, не затухая, преодолевать огромные пространства и людскую замкнутость. Это означает, что его "переносчик" должен очень легко перемещаться , не расходуясь при взаимодействии.

            Таким переносчиком служат жизнесберегающие технологии, под которыми понимаются любые знания, которые могут быть использованы для спасения человека от смерти  или продления его жизни. Отметим, что термин "технология" трактуется здесь предельно широко и включает в себя не только способы хозяйствования, но и государственное управление, воинское искусство, религиозные доктрины, средства коммуникаций, торговлю, медицину и т.д.

            Жизнесберегающие технологии имеют принципиальное отличие как от информации и знаний "вообще", так и от технологий в узко инженерном смысле этого слова. Касаясь всех и являясь общим делом, жизнесберегающие технологии не требуют для своего создания и распространения какого-то спецального механизма. Они создаются и распространяются в процессе повседневной деятельности людей.

            Обратим также внимание на то обстоятельство, что любая информация постепенно утрачивается (ни люди, ни материальные носители не вечны), и выжить во времени могут только те знания, которые постоянно используются и возобновляются, т.е. жизненно необходимы.

            Уровень развития жизнесберегающих технологий  определяется уменьшением среднего коэффициента  смертности  , достигаемым благодаря их действию, т.е.  , где   - коэффициент смертности пeрвобытного человека. Такой способ измерения технологического уровня является естественным и избавляет нас от необходимости строить оценочные шкалы для технологий  и "взвешивать" их по отдельности (в этом смысле теоретической демографии повезло так же, как экономике, в которой есть свой естественный скаляризатор - деньги, избавляющий нас от необходимости работать с матрицей взаимных меновых стоимостей различных товаров. Вместо неё можно использовать вектор цен).

            Будем далее полагать, что всё человечество характеризуется единым уровнем , то есть что время, необходимое для распространения (или независимого воспроизведения ) новых жизнесберегающих технологий, много меньше . чем . До демографического перехода средний коэффициент рождаемости   можно считать приблизительно постоянным и равным . При этом скорость роста народонаселения даётся формулой

(4)

Как уже отмечалось, жизнесберегающие технологии создаются людьми в процессе их повседневной деятельности, т.е. на основе уже имеющихся жизнесберегающих технологий. Следовательно, для скорости их появления  можно записать уравнение

,(5)

в котором константа  определяет трудозатраты , необходимые на увеличение  в  раз при постоянном .

Важно, что уравнение (4) (в отличие от уравнения (2)) линейно по . Поэтому оно в равной степени применимо как к человечеству в целом, так и к отдельным народам на том уровне приближения, когда мы пренебрегаем миграцией и считаем, что всё человечество имеет одинаковый уровень развития жизнесберегающих технологий. Данное обстоятельство позволяет переносить многие результаты , относящиеся к глобальному демографическому процессу на "исторический" уровень, и наоборот, распространять локальные представления на глобальный демографический процесс.

Интегрируя систему (4-5), приходим к соотношению

 (6),

 которое в предположении нулевого технологического уровня при отсутствии людей даёт основное уравнение теоретической демографии

(7)

Подстановка его в формулу (4) немедленно приводит к уравнению (2), ранее полученному путём анализа демографических данных.

Завершая обсуждение природы роста народонаселения, обратим внимание на одно любопытное обстоятельсттво. Если заменить уравнение (4) на формулу более общеговида

  (8),

с показателями  и , то принципиального влияния на конечный результат это не окажет. Квадратичная зависимость скорости роста от численности сохранится, хотя коэффициент  в уравнении (2) сменится на .

(Докажем это

Делим правую и левую части уравнения (5) на соответствующие значения (8)

Получим.

    

Интегрируя правую и левую части и предпологая , что произвольная постоянная равна нулю, получаем.

Подставляя полученное соотношение в (8), получаем(2))".

 

Получим решение дифференциального уравнения динамики человеческой популяции:

 

 

В эту формулу входят два произвольных параметра, которые должны быть константами динамики человечества. Физический смысл параметра   - более не менее ясен. Это тот момент времени, когда, в случае сохранения гиперболического закона роста человеческой популяции, число людей стало бы равным бесконечности. Такой режим теоретически предсказывается во многих задачах, связанных с горением  и является типичным при исследовании проблем самоорганизации. Кроме того, подобный режим встречается также при исследовании резонансных явлений [34]. Реально он, естественно, никогда не осуществляется, однако связанные с ним тенденции гиперболического роста параметра целого системы реализуются вплоть до очень высоких значений параметра целого. Однако момент, когда возникает взрыв, определяется  параметром  с достаточной степенью точности.

Сопоставление этой математической модели с экспериментальными данными, выполненное в [10], не только подтвердило универсальность указанного простого закона, не только позволило более точно определить момент времени , но и вычислить другую константу . Самое удивительное, что рост человеческой популяции удовлетворял этому закону  практически все 200000 лет, в течение которых существовало человечество. Отклонение от него началось лишь в конце семидесятых - начале восьмидесятых годов двадцатого века.

Значения величин  и  определённые на основе экспериментальных данных у различных авторов несколько отличается. Так, по данным Хорнера, приведённым в [10]=2025г.,

 

 

 

 

5.Модель роста комплексного параметра целого человеческой популяции. Демографический переход как вихревая особенность в поле комплексного времени

 

 

   Если идею о комплексификации параметра целого [18], [34] описывающего размножающиеся объекты применить к человечеству как к единой системе, то для описания динамики роста человеческой популяции можно ввести некое комплексное число , действительная часть которого характеризует рассмотренный выше параметр целого человечества и может быть приравнена к числу людей , а мнимая часть может характеризовать  некий информационный параметр , физический смысл которого ещё предстоит определить

 

.

 

Представленная в [10 ], [21 ] и частично приведенная выше экспериментальная зависимость  от времени может служить исходным материалом, который позволил бы нам подобрать соответствующую простую комплексную функцию . При этом время  также целесообразно считать комплексной величиной

 

.

 

На наш взгляд, важной задачей исследователя человеческого общества является отыскание такой простой комплексной функции от времени, действительная часть которой достаточно адекватно описывала бы имеющуюся экспериментальную зависимость . Как следует из приближенного анализа имеющихся экспериментальных данных, в течение очень долгого промежутка времени рост числа людей происходил по единому закону

,                                                 (4.39)

то есть по гиперболе. Величины  , определенные  в  [10]

 

 несколько отличаются от данных Хорнера, однако лежат в пределах допустимой точности.

Равенству (4.1) соответствует дифференциальное уравнение

 

                                          (4.40)

или

                                               (4.41)

Однако, начиная с 80-х годов ХХ века наступил мировой демографический переход [10 ]. Закон роста населения мира начал изменяться и, в соответствии со многими достаточно обоснованными прогнозами, число людей должно стабилизироваться на уровне 10-14 миллиардов человек, выйдя на эту асимптоту в ближайшие 50-100 лет. Этот демографический переход вместе с первичным режимом с обострением аппроксимируется в [10]  при помощи несколько более сложной функции, удовлетворяющей следующему дифференциальному уравнению

 

 ,                                     (4.42)

где, по данным [10 ]  лет.

 

Это последнее дифференциальное уравнение в среднем хорошо описывало практически всю кривую зависимости  вплоть до настоящего времени.

Несколько иная формула, немного более точно аппроксимирующая последние экспериментальные данные, дана в [50]

Необходимо отметить, что функция , представленная формулой (4.42) и ей аналогичные  ни коим образом  не является единственно возможной, однозначно определяющей будущее человеческого общества. Это следует хотя бы из того, что человечество - это система, управляющая (хотя бы частично) своим будущим и близких слабо отличающихся вариантов этого будущего бесчисленное множество. Однако , даже если объединить близкие варианты и исключить полную гибель человечества, то можно выделить, как минимум, три принципиально отличающихся друга сценария, каждый из которых будет рассмотриваться нами отдельно.

Продолжим рассмотрение сценария, предложенного С. П. Капицей [10 ], так как он кажется нам наиболее красивым и универсальным.

Если на оси  задана действительная часть некоей не имеющей особенности функции , то сама функция легко может быть однозначно определена во всей области. Однако в нашем случае искомая комплексная функция может иметь особенности в комплексной области,  и её отыскание может быть осуществлено путем поиска особых точек. Простейшая форма комплексного дифференциальное уравнения для её определения имеет вид:

 

.                                           (4.43)

 

Если ввести гидродинамическую аналогию, то закон (4.43) характеризует поток комплексного параметра целого  в комплексном времени, точка которого, соответствующая человеческой популяции, течет вдоль действительной оси и в настоящее время приближается к вихревой особенности, расположенной на расстоянии  над осью абсцисс.

 

Отделим в этом уравнении действительную часть от мнимой, считая, что .

                    (4.44)

Приравнивая отдельно действительную и мнимую части  комплексного дифференциального уравнения (4.44), получим

                                (4.45)

 

                                    (4.46)

Сопоставим формулу (4.45) с уравнением (4.42), построенным на основе анализа экспериментальных данных. Из этого сопоставления следует

 

.                                      (4.47)

Подставляя (4.47) в (4.45), (4.46), получим

                                  (4.48)

                                   (4.49)

Уравнение (4.48) в точности совпадает с уравнением (4.42), что означает, что наше комплексное уравнение дает результат, удовлетворяющий экспериментальным данным. Однако, мы получили еще одно действительное уравнение, физический смысл которого пока не совсем ясен.

Прежде, чем переходить к высказыванию тех или иных гипотез, необходимо проанализировать введенное нами дифференциальное уравнение, которое будет записано теперь в форме:

 

                                       (4.50)

 

Его аналитическое решение имеет вид  

 

                                  (4.51)

Если использовать (4.50) и (4.51), то искомому комплексному дифференциальному  уравнению можно придать еще одну форму

 

                        (4.52)

 

Отделим в равенстве (4.51) действительную часть от мнимой на оси .

          (4.53)

Приравнивая действительную и мнимую части  в уравнении (4.53), получим.

 .                                   (4.54)

.                                 (4.55)

При  величина  должна стремиться к нулю. Отсюда следует, что  и рост числа членов человеческой популяции определяется формулой:

,                                       (4.56)

совпадающей с аналогичным выражением в [10].

Преобразуем теперь несколько выражение (4.55)

Предположим, что

                                  (4.57)

 где  - некий параметр, характеризующий максимальный срок жизни человечества. В этом случае получим

                                   (4.58)

При таком определении величины  появляется новый параметр , внешний по отношению к нашему анализу, характеризующий границы, в которых величина , если она является неким энтропийно-информационным параметром, характеризующим человечество [18], остается положительной. Если считать, что человечество будет существовать столько, сколько оно уже существовало (что, вообще говоря, совсем не обязательно), то весь срок жизни человечества определяется величиной 2, и энтропийно –информационный параметр, характеризующий человечество, как в момент , так и в момент  окажется равным нулю.

Максимальное значение величины  должно наблюдаться при  и равняться

                                         (4.59)

или

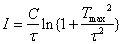                                           (4.60)

В эту формулу входит очень важный параметр 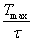, характеризующий отношение срока жизни человечества к сроку жизни одного человека, то есть грубо, с точностью до некоторого коэффициента, который можно принять приблизительно равным 2 - количество поколений людей, Так как 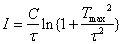 -достаточно большое число, то формула (4.60) может быть несколько упрощена.

                                                (4.61)

Последняя формула может быть приведена к виду

                                        (4.62)

Если вспомнить, что  характеризует приблизительно число поколений всех существовавших людей, и ввести обозначение , где - общее число поколений людей живших на Земле до момента , то мы получим формулу

,                                             (4.63)

смысл которой предстоит выяснить в будущем. Но ясно, что эта формула имеет прямое отношение к информационным процессам, происходящим с человечеством.  Наиболее естественным предположением является гипотеза о том, что этот параметр  характеризует введённую нами в [18] величину энтропии- информации, управляемой контроллером Человечества.

Наряду с рассмотренной выше нами  предложены и проанализированы ещё две возможные модели глобального развития человечества, причём высказана идея о том, что выбор той или иной модели во многом оказывается в руках самого человечества как системы, способной  моделировать своё будущее.

Динамика сложной  системы обычно имеет несколько возможных аттракторов, выбор между которыми может быть осуществлён в кризисные (бифуркационные) моменты её развития. Поэтому одной из задач научного исследования является  предложение обоснованных сценариев дальнейшего развития человеческого общества, поддающихся математическому моделированию.

В настоящее время рассматриваются три основных математических модели развития:

 а. резонансная (пессимистическая) модель, поддерживаемая экологами, соответствующая катастрофической  или плавной динамике сокращения числа людей, истощивших ресурсы Земли и не нашедших альтернативных источников существования;

б. вихревая (оптимистическая), предсказывающая стабилизацию  числа людей на некотором стационарном уровне при отсутствии серьёзных катаклизмов общечеловеческого масштаба, рассмотренная выше;

 в. космическая (сверхоптимистическая),  соответствующая

 выходу человечества за пределы Земли, а затем и солнечной

системы (частично рассмотренная в первой главе).

 

 

 

 

6. Параметр целого как параметр Планка.

Основные характеристики человечества как волны

 

 

В истории науки мало таких событий, которые подобно открытию Планком элементарного кванта действия за короткое время одной человеческой жизни привели бы к столь существенным последствиям. Это открытие не только во всё возрастающей степени становится основой для упорядочения знаний об атомных явлениях, которые за последние тридцать лет чрезвычайно возросли, но и привело одновременно к полному преобразованию принципов описания явлений природы.

 

Нильс Бор[52]

 

 

Человечество является не только обобщённой волной, в каждый момент времени состоящей из определённого количества квантов - людей.  Динамика роста числа людей определяет также некоторый процесс, обладающий волновыми свойствами, соответствующими тому определению волны, которое было предложено в [48] и приведено нами в [34]. " "…в самом общем случае мы определим волну как пространственно-временную эволюцию некоторого состояния." Это определение характеризует основное свойство волны, которое остаётся неизменным, независимо от типов волн, которые мы рассматриваем, а именно то, что при описании волновых движений мы следим не за частицами среды, в которой распространяется волна, а за параметром или совокупностью параметров, которые описывают состояние среды …" 

            Действительно, число людей, входящих в настоящий момент в состав Человечества, характеризует именно состояние волнового процесса динамики человечества в данный момент времени. В некоторый другой момент времени это число может либо сохраниться, либо измениться на некоторую величину, которую мы можем либо подсчитать, либо определить теоретически, например, по тем формулам, которые были выведены ранее. Однако, даже если это число (описывающее состояние человечества как обобщённой волны) не изменится, человечество как таковое будет состоять из того же числа людей, но не все из них будут теми же, что и в первый момент времени. Можно выбрать такой момент времени, например, отстоящий от первого на 200 лет, когда состав человечества полностью обновится. То есть человечество - это волна, проходящая через популяцию всех живших и живущих людей, а также людей, которые когда-нибудь будут жить. Именно эти люди и составляют ближайшую потенциальную среду, в которой распространяется волна состояния, характеризуемая числом живущих в настоящее время людей. Но если есть волновое движение, то оно должно иметь свой период, свою длину и амплитуду волны. Попытаемся определить и вычислить эти величины для человечества. Если применить к исследуемой волне разработанную нами классификацию волн, вихрей и дипольных структур и транспортно-информационных систем [ ], то в рамках проводимого нами в этом разделе анализа человечество может рассматриваться как грибовидная дипольная структура, перемещающаяся в среде всех существовавших и существующих людей и тех людей, которые будут существовать в будущем [34]. У такой структуры понятия длины и амплитуды волны могут быть отождествлены между собой и определяют некоторый характерный размер диполя.

Кроме того, указанный параметр может быть отождествлен, и мы постараемся это показать ниже, с обобщённым параметром Планка, то есть с квантом действия изучаемой структуры.

В качестве такого единого параметра может быть принята уже знакомая нам величина параметра целого - число людей, составляющих в данный момент человечество (или их суммарная масса). В отличие от квантовой механики, этот параметр, как нами было показано ранее, сам существенно изменяется во времени, и даже стремится выйти на режим с обострением, при котором теоретическое его значение стремится к бесконечности.

Однако, введённые определения были бы бессмысленны , если бы мы не получили никаких качественно новых результатов. Эти результаты могут быть получены лишь в случае, если мы включим в рассмотрение не рассматривавшийся нами ранее, но широко используемый в демографии параметры рождаемости и смертности, которым попытаемся дать новую - волновую интерпретацию, тем более, что один из них в работе [50] назван параметром , характеризующим жизнесберегающие технологии, что позволяет связать предлагаемое нами описание с более детальным триадическим описанием основных параметров человечества. Обычно рождаемость и смертность людей и других биологических объектов определяется в относительных величинах (в процентах или промилли) количество родившихся (или умерших) за год людей приходящихся на сто (тысячу) живущих. Как следует из  определения, эта величина имеет размерность обратную размерности времени и, следовательно, характеризует некоторую частоту. Примем, что эта частота и является  временной частотой человечества как волны. Введем волновые обозначения  - частота рождения

 ,

где  прирост числа людей за единицу времени (год) за счёт рождения (если считать популяцию замкнутой или рассматривать человечество в целом)

- общее число людей в данной популяции

Этот параметр характеризует относительный поток людей, входящих в рассматриваемую нами дипольную волновую структуру - человечество,- из среды, под которой мы в рамках данного рассмотрения понимаем всё количество живших, живущих на свете людей и людей, которые будут жить. Вхождение в такую волну в обычном понимании соответствует рождению нового человека - нового кванта человечества. 

            Человек живёт, то есть является частью волны, а затем выходит из неё, оставив по себе память и может быть навсегда включён в число живших на Земле людей.

В связи с этим необходимо ввести новое число -частоту ухода

, 

где  уменьшение числа людей за единицу времени (год)за счёт ушедших 

- общее число людей в данной популяции.

Величины  характеризуют частоту волнового потока, определяющего две величины

-

относительный прирост числа людей за единицу времени  (год)

Приведём эмпирические данные среднегодового прироста Человечества `, взятые из [49].

"Начиная с XVI века темпы прироста населения заметно возросли, развитие капитализма во многих странах сопровождалось ростом промышленного производства, подъёмом сельского хозяйства , увеличением производства пищевых продуктов, успехами медицины , что не могло не сказаться на демографических процессах. Резкое же ускорение роста населения началось со второй половины XVIII века , когда в ряде западноевропейских стран произошла промышленная  революция. В это время происходит первый (из статистически зафиксированных), причём, довольно сильный "демографический взрыв". Если с 1500 по 1750 гг. население увеличилось менее, чем на 300 млн человек (ежегодный прирост населения ранялся 0.2%), то за следующие 150 лет  (с 1750 по 1900 г)- на  910 млн. (рост составил свыше 0.4% в год) Особенно резкое увеличение темпов прироста характерно для второй половины XIX века (более 0.6% в год , в три раза выше, чем в XVI-XVIII веках), что можно объяснить начавшимся снижением смертности , особенно детской, при стабильном уровне рождаемости в промышленно развитых капиталистических странах Европы и Америки."[49. C.18]     

Среднегодовой прирост населения. (в%)

1900-1920                                                                                                                                                       0.5

1920-1940                                                                                                                                                       1.2

1940-1950                                                                                                                                                       1.0

1950-1955                                                                                                                                                       1.9

1955-1960                                                                                                                                                       2.0

1960-1965                                                                                                                                                       2.0

1965-1970                                                                                                                                                       2.0

1970-1975                                                                                                                                                       1.8

1975-1980                                                                                                                                                       1.7

1980-1983                                                                                                   1.7

Эта величина уже была подробно исследована нами ранее. Она характеризует относительную скорость изменения параметра целого (параметра Планка) человеческого общества. Именно исследование этой величины и её комплексного аналога и позволило нам сделать некоторые прогнозы о возможных путях развития человечества.

В работе [50. Рис 4 С.342]  представлен  график зависимости  от общего числа людей , построенный по данным [51].

 

 

 

 

 

№

млрд.

%

1

2.6

1.46

2

2.7

1.80

3

2.8

1.89

4

2.9

1.88

5

3.0

1.54

6.

3.1

1.76

7

3.2

2.08

8

3.3

2.12

9

3.4

2.04

10

3.5

2.03

11

3.6

2.04

12

3.7

2.04

13

3.8

2.01

14

3.9

1.94

15

4.0

1.85

16

4.1

1.77

17

4.2

1.72

18

4.3

1.71

19

4.4

1.71

20

4.5

1.72

21

4.6

1.72

22

4.7

1.71

23

4.8

1.69

24

4.9

1.68

25

5.0

1.69

26

5.1

1.69

27

5.2

1.66

28

5.3

1.60

29

5.4

1.54

30

5.5

1.47

31

5.6

1.42

32

5.7

1.39

33

5.8

1.35

34

5.9

1.30

35

6.0

1.28

36

6.1

1.24

37

6.2

1.21

 

 

 

Однако, из введённых параметров может быть построена и другая величина

-

Величина  характеризует собственную волновую частоту рассматриваемой нами волны- человечества.

Обратная ей величина

характеризует период введённой нами в рассмотрение волны.

Несколько преобразуем введённую ранее формулу для , умножив левую и правую её части на - число людей в популяции, это же число было нами принято за амплитуду и длины волны, параметр целого и параметр Планка.

Получившаяся величина может быть в нашей интерпретации определена как скорость перемещения волны - человечества относительно своей ближней среды: всех живших, живущих людей и людей, которые могут жить в будущем.

Величина   это просто общее число людей, живших до момента

С другой стороны, если подходить к этой проблеме с позиций волновой динамики, величина  характеризует действие человеческой популяции.

Решение последнего дифференциального уравнения имеет вид:

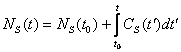
Или, если в качестве начального момента времени принять момент появления человечества, и в этот момент принять, что , то последняя формула принимает вид

.

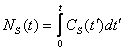Эта формула, являясь универсальной, позволяет, зная скорость волны , определить действие этой волны, в нашем конкретном случае - число живших до настоящего времени людей. Однако в этом определении присутствует неопределённость, связанная с тем, что сама величина  определяется неточно. Между родившимися и умершими существуют ещё живые Мы складываем фактически разные величины. И эта неопределённость в величине действия в точности равняется числу существующих в настоящий момент людей, которые ни к числу не родившихся, ни к числу ушедших не относятся. Это рассуждение в какой-то степени обосновывает наше предложение о том, что  может быть названо обобщённым числом Планка.

В каждый момент времени может быть построена  безразмерная величина.

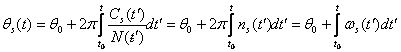
Эта величина может быть названа фазой волны, соответствующей человечеству как единой структуре.

В последней формуле величина - характеризует угловую частоту человечества как  волны в данный момент времени

Теперь перейдём к введению волновой функции, аналогичной волновой функции квантовой механики.

Введём новую комплексную переменную

.

Эта функция характеризует периодический волновой характер динамики развития человечества. Если , где то величина . Периодичность функции  характеризует периодичность смены поколений людей. Математически получаем почти полную аналогию с квантовой механикой.

Для того, чтобы аналогия была полной, необходимо ввести коэффициент , квадрат которого соответствует некоторой вероятности.

Тогда волновая функция человечества имеет вид

Попытаемся определить смысл амплитуды вероятности .

В каждый момент времени мы можем теоретически точно (хотя и это сделать не легко) , определить число живущих на Земле людей. По-видимому теоретически мы могли бы, хотя это уже проблематично, определить число людей, живших в любой момент времени в прошлом. Тем самым, мы можем с достаточной точностью определить параметр Планка для человечества в прошлом и в настоящем. Однако, уже определение этого параметра в будущем представляется проблематичным. Как нами было указано ранее, возможны, как минимум три возможных сценария дальнейшей динамики человеческой популяции, внутри каждого из которых с некоторой вероятностью можно наблюдать достаточно широкий спектр значений параметра целого (параметра Планка). Уже здесь появляется неустранимая (или устранимая лишь единственной реализацией) многозначность. Однако, вычисление числителя дроби, входящей в величину  представляет ещё более сложную и менее определённую проблему, не только для будущего , но даже для настоящего и прошлого. Таким образом, во всяком случае, в будущем, а , скорее всего, также и в настоящем и прошлом, мы будем иметь не какие-то конкретные значения комплексной величины , а дискретный (или почти непрерывный) спектр  возможных значений. Каждому значению этой функции в каждый момент времени может быть приписана некоторая вероятность реализации, а , следовательно, своя амплитуда вероятности.

Тем самым распределение значений волновой функции  в данный момент времени  характеризует распределение вероятности случайной величины  в данный момент времени. в прошлом, настоящем и в будущем.

При этом  является достаточно информативной функцией, так как она характеризует не только динамику человечества как обобщённой волны, в каждый момент времени, состоящей из определённого числа квантов - людей, но и динамику человечества как дипольной волновой структуры, включающей в себя в каждый момент времени все новые и новые кванты. Таким  образом волновая функция человечества является комплексной в двух смыслах. Она выражается некоторым комплексным конечномерным или бесконечномерным вектором, и одновременно она комплексифицирует группу широко используемых в демографии параметров, каждый из которых характеризует ту или иную сторону демографического процесса.

Однако, главным достоинством введения такой функции является её полная внешняя аналогия с волновой функцией квантовой механики. При этом удаётся отождествить широко используемые в демографии параметры с параметрами квантовой механики. Такое отождествление должно иметь далеко идущие последствия.

Первым из них является то, что проведённая нами для человечества процедура введения комплексной волновой функции является универсальной, справедливой для произвольных волновых движений, вихревых и дипольных структур и транспортно-информационных систем.  Тем самым она становится важной частью единой методологии исследования объектов природы.

Так как в случае квантовой механики введение аналогичной функции показало свою высокую эффективность, следует ожидать  не менее высокой эффективности и при исследовании волновых задач произвольной природы.

Более подробно следует остановиться на возможной интерпретации амплитуды вероятности, введённой нами при построении волновой функции человечества.  Если предположить, что мы хотим изучать будущую динамику человеческого общества, то о будущем мы можем говорить только предположительно и лишь описывать некоторое  распределение возможных состояний человеческого общества, а следовательно каждый момент времени для человечества является бифуркационным. При этом неопределенность реализации того или иного  состояния может быть определена как некий масштабный коэффициент , умноженный на логарифм амплитуды вероятности реализации этого состояния. Если на первом этапе принять этот коэффициент равным единице, то  формула для

может быть формально преобразована к виду

где, в случае конечного числа возможных состояний, каждому возможному значению фазы  соответствует заданная величина неопределенности именно этого исхода события

В показателе степени оказывается некоторое комплексное число, физический смысл которого нам более не менее ясен.

Действительная часть этого числа характеризует неопределённость (логарифм амплитуды вероятности реализации в момент времени  заданного значения  фазы . Мнимая часть характеризует саму фазу .Каждому возможному собственному значению волновой функции   соответствует логарифм этого значения, который мы, пользуясь терминологией  А.М. Хазена, назовём собственным значением оператора действия-энтропии-информации.[58][3][35]. Из полученного набора комплексных чисел  можно, пользуясь методологией квантовой механики, построить диагональный оператор, который мы назовём оператором действие-энтропия-информация.[18 ]

Определив математическое ожидание оператора действие-энтропия- информация, рассматриваемого как комплексная случайная функция, получим в каждый момент времени комплексную скалярную величину, которую назовём действием-энтропией-информацией будущего состояния человечества в некоторый момент времени   .

Наряду с вектором  можно ввести также осреднённую волновую функцию

, представляющую собой комплексное число, являющееся экспонентой действия-энтропии-информации.

 Вот некоторые количественные данные[19]

"Уровень смертности в первобытную эпоху (35тыс-15 тыс. лет тому назад) был очень высоким. Люди умирали от голода и болезней, погибали при нападении диких зверей, в столкновении с враждебными племенами и от стихийных бедствий. Особенно велика была детская смертность. Учитывая тяжёлые условия жизни первобытных людей, а также на основании найденных костных останков и сопоставления этнографического материала по племенам земного шара, находящимся на низких ступенях развития, предполагают, что средняя продолжительность жизни составляла в ту эпоху 20-25лет, то есть была в 3-3.5 раза меньше, чем сейчас в экономически развитых странах. Лишь немногие люди доживали в то время до 50 лет.

Уровень рождаемости в первобытную эпоху также, видимо , был высоким, во всяком случае он должен был превышать в среднем уровень смертности (составлявший около 45-50 человек на 1000 населения), так как при при меньшей рождаемости наши предки должны были бы вымереть. Высокая рождаемость поддерживалась главным образом ранними браками и практически поголовным охватом женщин брачно-половыми отношениями. В то же время репродуктивность, очевидно, не доходила до максимального уровня. Раннее вступление женщин в брачно-половые отношения, как правило, сразу же после наступления половой зрелости, частые беременности и роды в антисанитарных условиях, наряду с тяжёлой, полной лишений жизнью, приводили к быстрому увяданию, а часто и к ранней смерти женщин, сильно ограничивая тем самым их возможный детородный период.".[19. C.5].

            " Во второй половине XIX в. естественное движение населения Европейской России, по имеющимся данным, характеризовалось высокой рождаемостью (около 50 на 1000 населения) и высокой смертностью (около 35 на 1000 населения); очень велика была детская смертность - свыше 1/4 родившихся умирали, не дожив до года. "[19 C.19]

" К концу 1913 г. общая численность населения страны в современных границах СССР составила 159.2 млн. человек (Естественное движение характеризовалось очень высокой рождаемостью 47 на 1000 населения, высокой смертностью 30 на 1000 и повышенным естественным приростом.

"В первой половине 70-х годов XX- века во всём мире ежегодно рождалось около 120 млн. человек, или примерно 31.2 на 1000 жителей. Таким образом, коэффициент рождаемости снизился по сравнению с 1965-1969 гг., когда он составлял 32.1 на 1000 населения."[19.C.68]"

"Минимальный коэффициент рождаемости зафиксирован в 1977 г. в ФРГ - 9.5 на 1000 . Это беспрецедентно низкий уровень рождаемости, который никогда ещё не наблюдался ни в одной стране с большим населением. ."[19.C.69]"

 

 

 

 

 

К оглавлению

 

 

 

 

Рейтинг@Mail.ru