Оглавление

Часть I

Синергетика.

Информационно-волновая теория структур и систем

Глава 7

Квазидетерминированные процессы. Взаимодействие структур. Целостность процесса

Цепочка детерминированных и (или) бифуркационных событий, в результате которой происходит взаимодействие входящих в систему структур и появляются новые структуры или исчезают старые, была названа процессом.

С другой, внешней, стороны в графе структур и событий могут быть выделены определенные области (ветви), начинающиеся с какого-либо события и кончающиеся каким-либо другим событием, которые обладают некоторой независимостью от остальных областей графа . В связи с этим

под процессом можно понимать также некоторую, относительно независимую ветвь графа структур и событий

Сечения процесса по некоторому моменту времени могут быть представлены как вектор - матрицы данного процесса (как некоторой части графа структур и событий).

Если рассматривать процесс, в котором участвует та или иная система, не снаружи, с позиции всей системы, а изнутри, с позиций отдельной структуры, входящей в исследуемую систему, то для неё этот процесс можно представить некоторой индивидуальной траекторией внутри графа структур и событий, или траекторией внутри процесса (некоторым аналогом мировой линии Ньютоновой механики). При прохождении этой траектории, сохраняя в какой-то степени свою индивидуальность, структура вступает во взаимодействие с другими структурами системы, в течение некоторого времени формирует с ними комплексные структуры, затем эти структуры либо усложняются, включая в себя все новые элементы, либо распадаются с возвращением структур в прежнее состояние.

Если рассматривается процесс, ограниченный во времени, то можно ввести в рассмотрение некоторый отрезок времени, начало которого может считаться началом процесса, а конец - его окончанием. Введение такого отрезка времени и самого факта взаимодействия структур позволяет сформировать в системе некоторую метрику, характеризующую в первом приближении взаимодействие структур в системе, а следовательно, дающую количественную оценку ее целостности.

Предположим, что построена траектория некоторой структуры . При этом можно определить время , в течение которого структура участвовала в построении комплексных структур совместно со структурой . Это время составляет некоторую часть от времени прохождения процесса . Можно ввести понятие относительного времени взаимодействия структур и в процессе . Во многих случаях эта величина слабо зависит от величины , то есть от принятой нами условной длины процесса. Тогда ее можно считать устойчивой характеристикой взаимодействующих между собой структур и , или вкладом структур и в целостность процесса.

Такую процедуру можно осуществить для всех пар взаимодействующих структур и снабдить каждую из пар своей величиной относительного времени взаимодействия. Если величина стремится к единице, то структуры и совместно включены в новые структуры в течение всего исследуемого процесса и их совместный вклад в целостность процесса максимальный. Если , то структуры между собой не взаимодействуют.

Рассмотренный подход позволяет ввести внутри системы некоторую метрику, определяющую средние "расстояния" между отдельными структурами. Эти "расстояния" - могут быть определены как величины, обратно пропорциональные величинам .

(7.1)

Если принять , то есть "расстояние" структуры от самой себя равно нулю, то минимальное "расстояние" между взаимодействующими структурами соответствует случаю, когда , то есть когда структуры, сохраняя свою индивидуальность, взаимодействуют в течение вcего времени .

Чем меньше величина , тем больше введенное нами расстояние между взаимодействующими структурами. Если , то .

Если начать построение метрики с какой-либо одной структуры , то можно определить все структуры, которые взаимодействуют с ней в рамках данного процесса. Изображение их на шкале расстояний позволит включить сюда все структуры, расстояние которых от данной меньше бесконечности. Если для каждой из включенных в эту шкалу структур вновь построить шкалу расстояний до нее других структур, и эту цепочку действий продолжать до тех пор, пока новые структуры не перестанут появляться, мы получим систему, являющуюся подсистемой данной системы, и включающую в себя часть её элементов. Со структурами, не вошедшими в построенный нами подпроцесс, можно осуществить ту же операцию и построить другой подпроцесс изучаемого процесса.

Тем самым, введение предложенной метрики позволяет разбить изучаемый процесс (а может быть и весь граф структур и событий) на совокупность независимых друг от друга и не связанных между собой в течение исследуемого промежутка времени целостных процессов, внутренние метрики которых не связаны между собой.

Однако, предложенный алгоритм содержит принципиальный недостаток, который может быть ликвидирован введением некоторого нового параметра.

Ни одна из систем природы, ни один из исследуемых процессов не может быть полностью выделен из окружающего мира. Таким образом предложенная выше идеализированная схема не может быть реализована в своем чистом виде. Расстояния между отдельными структурами никогда не могут быть приняты равными бесконечности. Все структуры, существующие в природе находятся на некотором конечном "расстоянии" друг от друга, и отделение независимого процесса от всего процесса развития Вселенной невозможно.

Однако это можно сделать приближенно. Для этого необходимо ввести новое понятие - максимального радиуса взаимодействия структур в рамках данного процесса . Введение этой величины эквивалентно постулированию минимально допустимой величины относительного времени взаимодействия . Назначение этой величины является субъективным решением наблюдателя - исследователя в каждом конкретном случае. Чтобы исключить субъективность, можно ввести шкалу последовательно увеличивающихся (либо уменьшающихся) величин максимально допустимых расстояний между взаимодействующими структурами Введя соответствующее максимально допустимое расстояние между взаимодействующими структурами, мы можем повторить изложенную ранее процедуру. В этом случае в рассматриваемый подпроцесс попадут лишь те структуры, "расстояние" которых до хотя бы одной из структур, входящих в выделяемую подсистему, окажется меньше . Все остальные структуры попадут в другие подсистемы исследуемой системы или будут включены в поле данного подпроцесса.

Подобное разделение процесса на подпроцессы является приближенным, и степень приближения определяется принятой величиной - то есть величиной максимально допустимого расстояния между структурами, входящими в разделенные процессы.

Пусть имеем два отделенных друг от друга с радиусом процесса. Для каждого из них может быть вычислена своя максимальная величина целостности, которая может быть определена как сумма относительных времен взаимодействия всех входящих в систему пар структур.

Их число равняется ; где - число элементарных структур (квантов), входящих в систему.

Таким образом, целостность процесса может быть определена в соответствии с формулой

, (7.2)

где суммирование ведётся по всем парам взаимодействующих между собой структур.

Эта же величина может быть выражена через расстояния между элементарными структурами(7.1), входящими в систему

(7.3)

Максимальное значение целостности системы и соответствующего ей процесса достигается тогда, когда все входящие в неё элементарные структуры во все время процесса формируют единую структуру. В этом случае все значения оказываются равными 1, и величина целостности :

. (7.4)

Возможным также оказывается и введение относительной целостности процесса как отношения целостности процесса к максимальной целостности того же процесса.

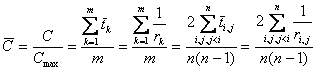. (7.5)

Одновременно с целостностью всего процесса целесообразно рассмотреть еще одну, близкую к ней величину, однако относящуюся к отдельной элементарной структуре.

Эта величина может быть названа связанностью -той элементарной структуры (кванта).

, (7.6)

Она характеризует суммарное относительное время взаимодействия данной структуры с остальными структурами системы. Максимальная величина связанности элементарной структуры, входящей в систему из элементарных структур, равна . Тогда относительная связанность структуры в рамках выделенного процесса определяется в соответствии с формулой

. (7.7).

Между связанностями структур, входящих в процесс, и целостностью процесса существует простая связь, определяемая следующей формулой.

. (7.8)

Аналогичная связь может быть установлена и между относительными величинами.

. (7.9)

Относительная целостность процесса определяется как среднее арифметическое от относительных связанностей структур, входящих в данный процесс.

Однако одного понятия максимального радиуса недостаточно для отделения одного процесса от другого. Это связано, например, с тем, что могут существовать элементарные структуры, расположенные на расстоянии, большем, чем от почти всех структур данного процесса, но на расстоянии, меньшем, чем , от одной или нескольких структур, однако имеющие значение - меньшее, чем аналогичное значение у структур, которые мы не включили в систему, участвующую в процессе по первому критерию. Тем самым, среди периферийных структур данного процесса мы выкидываем одни из них, вносящие больший вклад в целостность системы, по оставляем другие, вносящие меньший вклад.

Для более рационального разделения процессов следует в этом случае принять следующую процедуру. Первоначально исключить из процесса все структуры по критерию максимального радиуса. Затем для исключенных структур вычислить величины связанностей каждой из них. Определить максимальную величину связанности для выброшенных из процесса структур. Затем вычислить связанность всех оставшихся структур, и исключить из процесса все структуры, имеющие связанности, меньшие этой максимальной величины. В этом случае можно с достаточной степенью достоверности исключить из системы структуры по двум перевязанным между собой и не противоречащим друг другу критериям.

Однако, более подробный анализ показывает, что и этого оказывается недостаточно, так как не учитывается еще один - локальный критерий разделения.

Прежде, чем ввести такой критерий, необходимо рассмотреть понятие связи между двумя не взаимодействующими прямо между собою структурами.

Для введения такого понятия достаточно рассмотреть систему, состоящую из трех элементарных структур , взаимодействующих между собой с образованием комбинированных структур. Если предположить, что структуры между собой вообще не взаимодействуют, а структура взаимодействет как со структурой , так и со структурой , то можно, задаваясь величинами , определить связанность каждой из структур, а также целостность всего процесса. Если мы исключим структуру из анализа системы, то процесс в рамках нашего анализа автоматически разобьется на два независимых процесса, происходящих со структурами . Структура , оказавшись вне их, будет периодически включаться то в процесс , то в процесс , осуществляя опосредованную связь между ними. При этом интенсивность связи, в отличие от случая непосредственного взаимодействия между структурами, несимметрична относительно структур , например, . Одним из возможных критериев интенсивности связи может служить минимальное из двух значений , которое может быть обозначено . Структуру можно назвать агентом связи.

Таким образом, наряду с непосредственным взаимодействием элементарных структур между собой, целесообразно рассматривать еще один механизм - механизм взаимодействия через агентов связи, который может оказаться не менее важным, чем первый, особенно в случае анализа процессов, включающих в себя бифуркационные события.

При этом структура может быть включена в процесс, соответствующий той из оставшихся структур, связанность её с которой больше. А связь этой структуры с другой будет характеризовать взаимодействие разделенных процессов.

Пусть мы имеем некоторый процесс, происходящий с системой, состоящей из достаточно большого числа взаимодействующих между собой структур. В соответствии с разработанной выше процедурой попытаемся построить подпроцесс, включая в него только структуры, удовлетворяющие двум указанным выше критериям. Получим некоторую совокупность структур, образующих подсистему, входящую в первоначальную систему, которая может быть названа ее полем. Пусть подсистема, участвующая в этом подпроцессе может быть разделена еще раз на две группы структур, которые в рамках введенных нами ограничений не взаимодействуют непосредственно между собой и казалось бы в этом случае выделенный нами подпроцесс может быть разделен на две части. Однако мы не можем этого сделать, так как среди включенных в него структур существует одна или несколько, которые укладываются во все вышеуказанные ограничения и одновременно находятся на достаточно близком расстоянии от обеих указанных групп структур. Эти структуры могут быть названы структурами-связями или структурами - мостами.

Удаление таких структур из рассматриваемой подсистемы приводит автоматически к разделению её и процесса, в котором она участвует, на части. После такого разделения указанные структуры - связи или структуры - мосты, которые могут быть включены в процесс - поле, становятся основными элементами взаимодействия разделенных процессов.

Мы считаем, что выделение в процессах и подпроцессах одной или нескольких структур-мостов - и удаление их из подсистемы в поле должно стать частью алгоритма разделения сложной системы на подсистемы, сложного процесса на подпроцессы.

При этом должно быть заранее задано число структур, которые должны быть удалены одновременно. Самым простым способом является перебор всех сочетаний из структур, уже вошедших в подсистему по числу структур, которые должны быть удалены из подсистемы начиная от единицы и до заданного числа. Для каждого такого сочетания должна быть осуществлена проверка на разделимость. И если она выполняется, то соответствующие структуры удаляются из системы, а сама она разделяется при этом на части. Выброшенная при такой процедуре структура может быть либо отнесена к полю, либо включена в ту часть разделенного процесса, с которой она больше связана, суммарная связанность со структурами которой оказывается максимальной.

Среди структур-связей может оказаться особый класс, обладающий следующим свойством. Такая структура связана с несколькими структурами одного подпроцесса и может быть после разделения включена в этот процесс, и лишь с одной структурой другого подпроцесса, которая обладает аналогичными свойствами относительно своего подпроцесса. В этом случае в каждом процессе существует по структуре, каждая из которых связана лишь с одной определенной структурой другого процесса. Такие мостовые структуры могут считаться граничными структурами процессов. По ним также можно отделять процессы друг от друга. Если в разделяемом процессе существует любое количество граничных структур, при процедуре разделения они все должны быть выброшены, чтобы затем присоединить соответствующие структуры каждую к своему процессу.

Пусть имеем два процесса, (1 и 2) отделенные друг от друга с некоторым радиусом . Тогда в рассматриваемом случае под мерой взаимодействия процессов можно понимать некоторую величину, которая может быть определена следующим образом. Внутри каждого из процессов существуют структуры, взаимодействующие, хотя и слабо, со структурами другого процесса. Величина этого взаимодействия определяется для каждой структуры одного из процессов, как и ранее, суммарным относительным временем взаимодействия со всеми структурами другого процесса. Эта величина может считаться интенсивностью взаимодействия данной структуры, принадлежащей к процессу 1, со всеми структурами, принадлежащими к процессу 2, или связанностью структуры процесса 1 с процессом 2.

(7.10)

В последней формуле , - номер структуры, принадлежащей к первому процессу. - номер структуры, принадлежащей ко второму процессу. - число структур, входящих во второй процесс.

Полная величина взаимодействия между процессами (или системами, участвующими в процессе) определяется по формуле:

. (7.11).

Пусть имеется некоторый процесс, для которого выполнена описанная выше процедура разделения процесса на составляющие подпроцессы. Если принять максимальный радиус взаимодействия равным бесконечности, то процесс оказывается неразделимым. Уменьшая максимальный радиус, мы увеличиваем число подпроцессов, на которое может быть разделён наш процесс. Аналогично, увеличивая при постоянном значении максимального радиуса величину допустимого числа мостовых структур, мы также можем увеличить число подпроцессов, на которое может быть разбит наш процесс.

При этом для каждого значения указанных параметров получается свое значение величины взаимодействия выделенных подпроцессов.

В предельном случае, когда принятое нами максимальное расстояние между структурами оказывается меньше 1, исследуемый процесс разделяется на подпроцессов, каждый из которых описывает динамику отдельной элементарной структуры. Зависимость числа выделяемых подпроцессов, а также степени их взаимодействия от изменения двух основных задаваемых исследователем параметров позволяет достаточно подробно проанализировать внутреннюю топологию исследуемого процесса - составить его "образ". При этом наиболее характерными становятся те значения управляющих (управляемых нами) параметров, при которых происходит качественное изменение картины, а именно существенно изменяется число рассматриваемых подпроцессов. Тем самым, мы получаем «паттерн» исследуемого процесса и каждого из его подпроцессов, который в течение некоторого времени может считаться постоянным. Взаимодействие подпроцессов в рамках этого паттерна может быть названо фоновым взаимодействием.

Предположим, что в рамках данной большой системы, состоящей из взаимодействующих подсистем, паттерн взаимодействующих подсистем меняется медленно по сравнению с частотой, с которой взаимодействуют между собой отдельные структуры. В этом случае можно ввести два масштаба времени - масштаб времени, соответствующий взаимодействию структур внутри подсистем, и масштаб времени, соответствующий характерным изменениям паттернов фонового взаимодействия. Характерное время , введенное ранее, занимает промежуточное положение между этими двумя масштабами. При исследовании взаимодействия процессов в макро-временном масштабе можно ввести следующую процедуру. Рассмотреть макроскопический масштаб времени, внешний по отношению к масштабу , и в рамках этого масштаба ввести в рассмотрение понятие времени начала отсчета - текущее время. Для каждого значения текущего времени, рассматривать малый по сравнению с внешним масштабом промежуток времени , в рамках изменения которого паттерн процесса, который на этом промежутке можно считать стационарным, слабо меняется. Этот паттерн можно считать присущим макроскопическому моменту времени .

Аналогичную процедуру можно осуществлять для некоторой последовательности значений . Если изменения паттернов окажутся гладкими, то можно ввести асимптотическое представление о гладкой зависимости паттерна взаимодействующих процессов от времени, о скоростях изменения паттерна от времени - то есть построить соответствующие дифференциальные уравнения.

Рассмотрим три характерных случая макровременного взаимодействия.

Непосредственное взаимодействие двух выделенных процессов. Пусть при помощи описанной выше процедуры нам удалось все основные структуры, включённые в данную систему, отнести к двум различным подсистемам, то есть разделить некоторый процесс на два подпроцесса.

Пусть на некотором промежутке времени оба подпроцесса можно считать установившимися. Тогда в каждый макроскопический момент времени возможно построить паттерн обоих взаимодействующих процессов и вычислить их фоновое взаимодействие.

Выберем некоторые значения управляющих параметров и допустимого числа удаляемых мостовых частиц. Затем выполним с этими значениями управляющих параметров процедуры разделения процессов и вычисления их фонового взаимодействия для различных моментов времени. Тем самым получим сечение по управляющим параметрам последовательности паттернов взаимодействующих процессов во времени. При этом на каждом шаге по времени вследствие изменения паттерна будет изменяться не только величина фонового взаимодействия процессов, но, что намного более важно и существенно, число структур, которые входят в каждый из процессов. Мостовые и граничные структуры будут менять свои связи в обоих процессах и переходить из одной подсистемы в другую, из одного подпроцесса в другой. При этом они могут уходить в центральную часть процесса. Может происходить и обратное явление ухода структур на периферию процесса . Тем самым, хотя разделение на два процесса будет оставаться, внутренняя структура, в том числе и целостность каждого из них изменяются значительно. При этом наиболее важным является тот факт, что многие элементарные структуры, входившие сначала в один процесс через некоторое время оказываются в другом.

Пусть в момент времени в первой из взаимодействующих систем находится основных структур, а во второй . Рассмотрим некоторый новый момент времени , отличающийся от на величину . В этот момент состав систем, участвующих в первом и втором процессах, изменится. В первой из взаимодействующих систем окажется элементарных связанных между собою структур, а во второй системе -.

Целостность подпроцессов - обобщённых волн - формируется на микровременном уровне. Однако с изменением макровремени, два взаимодействующих целостных процесса претерпевают существенные изменения. Структуры могут переходить из одной подсистемы в другую, из одного процесса в другой.

За промежуток времени из первой системы во вторую перейдет элементарных структур, а из второй системы в первую - структур. Тогда, если элементарные структуры никуда не исчезают, то есть выполняется закон сохранения элементарных структур, то мы можем получить следующие соотношения.

- (7.12)

Введем величину

. (7.13)

Отношение величины к промежутку времени , определяет некоторую среднюю скорость изменения взаимодействующих систем.

(7.14)

Если участвующие во взаимодействии элементарные структуры имеют приблизительно одинаковую меру, то, умножая правую и левую части последнего равенства на эту величину, которую обозначим , получим следующее равенство

. (7.15)

Осредненная разность потоков меры между процессами определяется как отношение приращения меры в процессе, увеличившем свой "объём", к исследованному промежутку времени.

Выберем конечную последовательность уменьшающихся отрезков времени таким образом, чтобы оставалось значительно больше . И построим последовательность осредненных разностей потоков. Если график изменения асимптотически выходит на величину,

(7.16)

то эта величина может быть названа величиной неравновесности, или асимптотической производной от изменения меры процессов по времени.

При этом для каждого из взаимодействующих процессов эта величина может быть взята со своим знаком. Для процесса, увеличивающего свою меру, - со знаком плюс, для процесса, уменьшающего свою меру - со знаком - минус.

Если первый процесс увеличивает меру, то

Во многих случаях можно забыть о последовательности вывода этих асимптотических соотношений и опустить индекс , обращаясь с соотношениями, входящими в предыдущие формулы как с обычными производными.

(7.17)

Последние формулы могут оказаться справедливыми и в случае, если элементарные структуры специально не могут быть выделены, а обмен "мерой" происходит за счет более сложных структур, однако, измеряемых одной аддитивной мерой, хотя значения её могут быть различными для каждой из участвующих в процессе структур. При этом величина вычисляется как модуль разности суммы мер структур вышедших из данного процесса и суммы мер структур, в него вошедших.

Анализируя динамику изменения меры каждого из взаимодействующих процессов, мы можем перейти к рассмотрению либо системы двух связанных между собой дифференциальных уравнений , либо к системе итерационных соотношений - характеризующих изменения основной аддитивной меры взаимодействующих процессов.

Макро-временное взаимодействие может быть описано еще одним параметром, характеризующим интенсивность обмена элементарными структурами между взаимодействующими процессами. Эта величина определяется как полусумма числа структур вошедших за промежуток времени , например, в первый процесс, и числа структур, вышедших из него.

(7.18)

Разделив величину на и проведя асимптотическую процедуру, аналогичную той, которая выполнялась нами в предыдущем случае, получим асимптотическую скорость обмена структурами

(7.19)

По аналогии с предыдущим можно ввести также величину скорости обмена мерой

. (7.20)

Интересен случай, когда в процесс входят все новые и новые структуры, а уходят из него уже побывавшие в нём. В этом случае можно выбрать такой промежуток времени , при котором в конце промежутка в одной из систем не останется ни одной из структур, бывших в ней в начале промежутка. Тем самым, процесс остается все тем же процессом , но в нем уже нет ни одной старой структуры. При этом может оказаться так, что картина связей - уже между новыми структурами, занявшими место прежних будет сохраняться той же. В этом случае процесс становится похожим на классическую волну, сохраняющую свой паттерн при полной замене структур, в нее входящих. Для такого процесса может быть введена и новая величина , период циркуляции структур внутри процесса, приближенно определяемая как отношение

(7.21)

Здесь - величина аддитивной меры, соответствующей данному процессу.

Период циркуляции структур характеризует свой для каждого из взаимодействующих процессов период процесса как некоей циклической волны, перемещающейся по полю структур, входящих в оба взаимодействующих процесса. Фактически этот период характеризует то, что мы называем обменом веществ.

Однако, этот случай является лишь предельным возможным случаем волнового взаимодействия процессов.

Другим предельным случаем является вариант, когда во взаимодействии участвуют только те мостовые структуры, которые были названы нами пограничными.

Предположим, что при взаимодействии систем, входящих в процессы, не происходит переход структур из одного процесса в другой. Считаем, что все мостовые структуры, осуществляющие основное взаимодействие - являются граничными; каждая из них связана лишь с одной граничной структурой другого процесса. Сцепленные между собою граничные структуры формируют некоторые новые структуры. Совокупность таких структур может быть названа общей границей обоих взаимодействующих процессов. Динамика взаимодействия процессов в этом случае характеризуется динамикой их общей границы.

Сама граница становится новой системой, обладающей своей динамикой, а оба взаимодействующих процесса становятся полем существования такой системы. Это один из механизмов формирования и существования умеренно-нелинейных волновых структур (второй класс нашей классификации). Возникают три специфически взаимодействующих процесса. Два первых взаимодействуют между собой через третий процесс - процесс границу, процесс посредник, делегируя в него свои граничные структуры.

Динамика такого взаимодействия может быть классифицирована следующим образом.

1. Граница остаётся неизменной. Одни и те же структуры одного процесса взаимодействуют с одними и теми же структурами другого. Процесс взаимодействия может считаться стационарным.

2. Взаимодействие качения. Структуры, образующие границу не меняют своих партнеров. Они могут либо разрывать свои связи и уходить внутрь своих процессов, либо образовывать новые, выходя на границу.

3. Взаимодействие скольжения. Структуры, входящие в границу, меняют своих партнеров, однако постоянно остаются на границе.

4. Смешанное поведение.

В результате взаимодействия качения и смешанного поведения граница может либо захватить один из взаимодействующих процессов, либо исчезнуть. При этом процессы перестанут взаимодействовать между собой.

Между двумя рассмотренными выше механизмами макровременного взаимодействия процессов лежит область механизмов взаимодействия, занимающая все возможные комбинации с существованием границ и обмена структурами между ними.

При этом могут появляться переходные слои, элементы которых, не являясь границами в указанном выше смысле, активно участвуют во взаимодействии, тогда как основные части - ядра - систем участвующих в процессах, в их взаимодействии участвуют лишь через внутреннее взаимодействие с переходными слоями. Эти переходные слои чаще всего могут быть отнесены ко второму классу нашей классификации - умеренно-нелинейным волнам. [12]

Одним из главных результатов взаимодействия может оказаться слияние процессов, Противоположным событием является, например, расщепление одного из взаимодействующих процессов, или обоих на несколько более мелких подпроцессов, которые либо будут существовать раздельно, взаимодействуя между собой, либо войдут в систему последовательных расщеплений, аналогичных сценарию возникновения хаоса в результате цепочки бифуркаций.

Физическим примером такого взаимодействия может являться формирование брызг.

Социологическим - формирование и распадение Империй.

Второй вариант взаимодействия процессов - взаимодействие некоторой системы и её поля.

Этот вариант в некотором смысле является частным случаем предыдущего. Однако второй из взаимодействующих процессов оказывается как бы вне первого. Он содержит значительно больше элементарных структур. Дополнительной существенной особенностью взаимодействия системы и поля обычно является тот факт, что элементарные структуры, формирующие поле, часто имеют значительно меньшие значения меры, чем структуры, формирующие систему, что придает взаимодействию специфические особенности.

Во многих случаях в поле может быть введена непрерывная континуальная геометрия. Введение такой геометрии требует достаточно тонких рассуждений, позволяющих перейти от дискретной метрики взаимодействующих структур, введенной нами ранее, к непрерывной римановой метрике в мерном непрерывном многообразии, что позволяет использовать для исследования особенностей взаимодействия структуры и ее поля развитую в настоящее время теорию гладких расслоений [24].

Третий вариант , когда два процесса взаимодействуют при наличии поля, вносит нечто принципиально новое в вышеприведенное рассмотрение.

Кроме непосредственного взаимодействия процессов, описанного в случае первого варианта, возникает еще один механизм взаимодействия - взаимодействие через поле.

Каждый из взаимодействующих процессов обменивается с полем элементарными структурами. Тем самым, через изменение поля происходит дополнительное к прямому полевое взаимодействие процессов. Те структуры, которыми поле обменивается с одним из процессов влияют на характеристики поля, тем самым влияют на характер обмена структурами между полем и вторым процессом. Это взаимное влияние оказывается интегральным - волновым - происходящим одновременно с существенным изменением поля, через которое и происходит само взаимодействие процессов.

Однако, в некоторых случаях взаимодействие процессов через поле оказывается и более непосредственным. Структуры, вышедшие в поле из одного процесса, могут достаточно быстро попасть из поля в другой процесс. Поток таких структур - агентов формирует еще один механизм взаимодействия процессов, который может быть назван взаимодействием посредством связей между двумя процессами, осуществляемыми через поле.

Интенсивность связей определяется, как и ранее, числом структур-агентов (или их суммарной мерой), вышедших из одного процесса и вошедших в другой. Все рассуждения, которые были проведены ранее, могут быть повторены для связей. Однако, в данном случае элементарная структура, выйдя из одного процесса, некоторое время находится в поле, и лишь затем оказывается в области действия другого процесса. Появляется новый параметр - время задержки связи. Поле формирует внешнее пространство, в котором структуры-связи функционируют, пока они не попали из одного процесса в другой.

К оглавлению