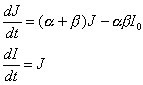В раздел «Клиодинамика и Синергетика»

 

 

Памяти наших родителей  Басина  Абрама  Моисеевича

                                              Басиной Цицилии Рувимовны

                                           Смирнова Ивана Ивановича
                                                          Смирновой Полины Викторовны

 

 

 

 

СИНЕРГЕТИКА

 

Материалы  к  Энциклопедии

 

Г.И.Басина,   М.А.Басин

 

НИЦ "Синергетика"

Санкт-Петербургского союза ученых

 

Санкт-Петербург

2016

 

 

УДК 167.0

ББК 32.8

Б 27

 

 

 

Басина Г. И., Басин М. А. Синергетика. Материалы к Энциклопедии. СПб.: НИЦ «Синергетика» Санкт-Петербургского союза учёных. 2016 год.

 

 

 

 

 

 

 

 

 В предлагаемом читателям и посетителям Internet сборнике Этюдов представлены небольшие Эссе, каждое из которых посвящено отдельной проблеме теории динамических систем и Синергетики. Авторы стремились представить читателю в основном, новые идеи и результаты полученные ими в последние годы . однако эти новые результаты вплетены в ткань уже известных материалов, полученных ранее исследователями, заложившими основы Синергетической парадигмы.

 В названиях этюдов сборника отражены наиболее существенные   объекты исследования, на которые авторы хотели бы обратить особое внимание читателей.

 

 

© Басина Г. И.,  Басин М. А.

 

 

 

 

 

 

Содержание

                                                                                    

   Введение. Что такое Синергетика

 

Басина  Г. И.,Басин М. А. Синергетика. Энциклопедия . План монографии

 Басин М.А, Шилович И.И. Синергетика. Её особенности как науки

          Материалы 50 Семинара “Синергетика и методы науки”,
посвящённого 80-летию со дня рождения д.ф.-м.н., профессора

Баранцева Рэма Георгиевича и. 50-летию научной деятельности д.т.н. Басина Михаила Абрамовича.

       1. Barantsev Rem Georgievich. Curriculum vitae

       2. Баранцев Рэм Георгиевич. Автография.

       3.Scientific,Pedagogic and Social Activities of Professor, Doctor of Technical Sciences Basin Mikhail Abramovich –A Short Summary

      4. Краткая хапактеристика научной, педагогической и общественной деятельности профессора, доктора технических наук Басина Михаила Абрамовича.

     5. Краткая характеристика научной и общесвенной деятельности Басиной Галины Ивановны.

     6. Басина Г. И., Басин М.А..Синергетика. Комментапий к тринитарной методологии Р.Г. Баранцева.

     7 .Дтн,Профессор Ровинский Реомар Ефимович. Синергетика. Новпе научное направление

     8.  Дф-м н. Профессор Баранцев Рэм Георгиевич. Что такое синергетика.

    9. Дф-мн Ланда  Полина Соломоновна. Нелинейные колебания и волны

 

Этюд 1.Три языка Синергетики.

Этюд 2.Параметр целого.            

Этюд 3. Комплексный параметр целого. Обзлр выполненных исследований.

Этюд 4. Развитие структур. Динамика Ферхюльста.

Этюд 5.Резонансы в конечномерных динамических системах

Этюд 6.Бифуркации экспоненты окружности. Числа Абрама Моисеевича Басина.

Этюд 7.Экспоненты окружности как фазовые кривые нелинейных динамических      систем.

Этюд 8. Комплексный степенной многочлен как источник квтастроф.

Этюд 9 Экспонента окружности как фазовая траектория нелинейного итерационного соотношения.

Этюд 10. Многомерные степенные комплексные смстемы итерационных соотношений. Экспонента окружности как  одна из форм фундаментального решения системы.

Этюд 11. Алгебраические и спиральные комплексные числа.

 Этюд 12. .Комплексная динамика живого. 

Этюд 13. Введение внутреннего и внешнего времени в теорию динамических систем.   .

Этюд 14 Самоорганизация в распределении масс элементарных частиц.

Этюд15. Триады в Синергетике

Этюд 16. Основная триада Человеческого общества

Этюд 17. Линейные волны и волновые резонансы.

Этюд 18.. Классификация волн, вихрей, грибовидных и древовидных структур и транспортно-информационных систем.

Этюд .19 Умеренно-нелинейные волны.

Этюд 20.Вихревые и  грибовидные структуры. Транспортно-информационные    системы

Этюд21                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                 Синергетический метод исследования транспортных систем

Этюд 22. Вихре - волновой и  (или) структурный резонанс. История открытия.

Этюд 23. Вихре-волновой и (или) структурный резонанс. Концепция работает

Этюд 25. Ода границам.

Этюд 26. Границы и жизнь.

Этюд 27. К теории творческого потенциала.

Этюд 28. О новом типе крыла с максимальиым  аэро-гидродинамичкским качеством.

Этюд 29.  Вероятностный.анализ бифуркационных событий, в которых участвует система.

Этюд 30.       Энтропия и информация бифуркационного события.

Этюд 31.Волновой вектор-матрица события

Этюд 32.Целостный компьютер. Путь в Synergonet.

Этюд 33.Структура. Поле. Контоллер.

Этюд 34.Вихре-волновой и (или) структурный резонанс. Нана-технологии. Жизнь. Экономика.

Этюд 35 ..Об изучении сложных структур.

Этюд 36. О транспорте энергии и информации в волнах и структурах.

Этюд 37 Квазидетерминированные процессы. Взаимодействие

структур. Целостность процесса.

Этюд 38.Бифуркационные процессы.

Этюд 39. Взаимодетвие бифункационных процессов.

Этюд 40. Теория Synergonet.

Этюд 41.Человечество. Синергонет.

Этюд 42. Синергетика.Число Хавинсона. Комментарий

Этюд 43.Осовременном этапе развития Чпловечества..

 

 

 

 

 

 

 

 

Введение

Что такое Синергетика.

 

 

                                     В    отличие   от большинства  наук,   возникавших,

 как правило, на стыке двух ранее существовавших и

характеризуемых   проникновением   метода    одной

науки в предмет другой, она (Синергетика) возникает,

опираясь  не  на  граничные,  а  на  внутренние точки

различных   наук,  с  которыми  она имеет  ненулевые

пересечения:  в  изучаемых (ею) системах, режимах и

 состояниях физик, биолог, химик и математик видят

 свой материал, и каждый из них, применяя методы

 своей науки, обогащает общий запас (её) идей и методов.

Ю.А. Данилов, Б.Б. Кадомцев [1]

 

    Если построить системную триаду научного знания [1]

 

 

                                                         Философия

                                                        /                 \

                                     Математика------- Конкретные науки,

 

то Синергетика проектируется в центр и приподнята над плоскостью этой триады, становясь её ядром и одновременно осуществляя связи между её элементами. Появление Синергетики связано с тем, что в каждом из элементов триады появились возможности для изучения самых сложных проблем – проблем самоорганизации материи. Синергетика обобщает эти возможности, и, синтезируя их, порождает новые. Границы Синергетики лежат в областях её сращивания с элементами триады, и их установление происходит в творческой конкуренции идей, амбиций и мнений. Задача Синергетики будет выполнена, и границы её будут определены, если триада превратится в полноценную системную тетраду, каждый элемент которой будет иметь своё ядро и связи с другими элементами. Ни попытки уничтожить Синергетику как не имеющую своей сферы исследований, ни противоположные попытки заменить Синергетикой всю базовую триаду научного знания не будут продуктивными.

    Значительный вклад в развитие синергетических исследований внесли Санкт-Петербургские учёные. С мая 1993 года по инициативе выдающегося учёного и общественного деятеля В. Д. Поремского в Санкт-Петербурге работал Семинар «Синергетика и методы науки», а с октября 1995 года – функционирует научно-исследовательский центр «Синергетика». Работы центра были поддержаны четырьмя грантами РФФИ (руководитель: проф. М. А. Басин) и тремя грантами РГНФ (руководитель: проф. Р. Г. Баранцев). Сотрудниками центра опубликовано более двухсот статей и двадцати сборников и монографий [3].

 

 При мысленном выделении объекта из природы мы составляем в мозгу его образ, даём ему имя и вводим в рассмотрение два числа: единица и нуль, - характеризующие соответственно существование и отсутствие объекта. Тем самым, мы вводим в рассмотрение три языка Синергетики и науки вообще:

а) язык математики,

 б) язык образов,

 в) язык слов.

 Эта триада соответствует семантической триаде Р.Г. Баранцева[2]:

 

–                                                        интуицио

                                                              /          \

                                                        рацио –эмоцио.

 

Синергетика внесла в использование этих языков специфические особенности и новые связи. Достижения качественной теории динамических систем и нелинейных волн, структур и систем, изучение информационных процессов, внедрение тринитарной методологии и мягких математических методов асимптотической математики привели к появлению новых мысленных и графических образов, новых слов и определений, новых математических понятий, которые благодаря синергетическим исследованиям внедряются во все элементы основной триады научных дисциплин.

Целостная система, которая может быть названа одним словом, при математическом описании приближённо представляется действительной скалярной мерой – параметром целого. Удачный выбор параметра целого является следствием адекватности того мысленного образа изучаемого объекта, который сложился на первых этапах эмпирического исследования, реальному объекту. Параметр целого должен быть выбран таким образом, чтобы он легко определялся эмпирически или вычислялся и характер его зависимости от времени был устойчив для ряда аналогичных систем (квантов обобщённой волны). Если мы оставляем при исследовании сложного объекта лишь одну обобщённую координату (меру, параметр целого), то в качестве неё можно использовать величину, характеризующую объём многообразия координат, более детально описывающих систему. Это может быть геометрический размер или объём, положение в пространстве, действие, энергия, масса системы, энтропия или информация, количество денег в экономике, прибыль, количество слов в языке и даже переменная возможность существования самой системы. В ряде случаев можно принять за параметр целого изучаемого объекта число элементов - квантов, которые включены в объект как в обобщённую волну; если каждый из них имеет свою меру или параметр целого и эти меры аддитивны, то - суммарную меру всех квантов. Введение параметра целого подразумевает значительное информационное сжатие, и поэтому динамика его изменения не полностью определяет динамику системы. Динамика параметра целого может быть приближённо описана либо в виде итерационного процесса, либо в форме дифференциального или интегрального уравнения. Качественный анализ такого рода систем с дискретным и континуальным числом состояний позволил  проанализировать возможные особенности качественного изменения этого параметра для различных классов структур и систем.

В настоящим сборнике представлены принципиально новые теоретические результаты, которые были получены на пути комплексификации параметра целого и качественного исследования дифференциальных уравнений и итерационных процессов в области комплексного переменного. . Обнаружены новые иррациональные числа, играющие существенную роль в исследовании нелинейных комплексных систем, названные в честь выдающегося учёного Абрама Моисеевича Басина числами Басина.

 Однако анализа нелинейной динамики одного, хотя и удачно выбранного, параметра целого обычно бывает недостаточно. При более детальных исследованиях вводится несколько обобщённых координат, изменение которых более подробно характеризует динамику системы. В соответствии с идеями Г. Хакена [4] и Р. Г. Баранцева [2] можно предположить, что оптимальным с точки зрения асимптотического анализа является тринитарное описание динамической системы. Теория нелинейных динамических систем с конечным и бесконечным числом координат в настоящее время интенсивно развивается. Предложены различные формы классификации систем и их математических моделей.

В предлагаемом читателю собрании Этюдов отражены некоторые новые аспекты исследований авторов, вошедшие в арсенал синергетической парадигмы. . Связь между ними не лежит на поверхности. Для её отыскания читателю потребуется некоторое умственное напряжение, которое, как мы надеемся, принесёт ему дополнительную пользу и эстетическое наслаждение..

 

 

Литература

 

 

1.Данилов Ю.А., Кадомцев Б.Б. Что такое Синергетика?//Нелинейные волны. Самоорганизация. М.: Наука. 1983. С. 5-16

2. Баранцев Р. Г. Синергетика в современном естествознании. М.: Едиториал УРСС.2003.144 с.

3. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб.: Норма. 2006. 56 с.

4.Хакен Г. Синергетика. М.: Мир. 1980. 414 с.

 

 

 

 

 

 

 

 

 

 

 

Басина Галина Ивановна

Басин  Михаил  Абрамович

 

Синергетика. Энциклопедия

 

План монографии

 

Введение. Что такое Синергетика ?

 

1.Синергетика. Её особенности как науки.

2. Основные научные результаты, составившие базу Синергетики.  

3. Internet и  Синергетика.

 

Часть первая.

Синергетическая методология.

Конечномерные динамические системы.

 

Глава  первая

Общие подходы к исследованию структур и систем.

Три языка Синергетики

 

1. Выделение объекта  исследования.

2. Использование трёх  языков Синергетики.

3. Проведение лингвистического анализа.

4. Предварительная классификация процесса или объекта.

5. Включение процесса (объекта) в систему квант-волна.

6. Проблема времени.

7. Словесная история объекта.

 

Глава  вторая

Дискретные конечные структуры.

Компьютерная реализация теории.

Концепция целостного компьютера .

 

1.Динамика детерминированных структур с конечным числом состояний.

2. Обратимые детерминированные процессы.

3. Необратимые автономные детерминированные процессы .

4. Бифуркационные процессы с конечным числом состояний.

5  Энтропия бифуркационого процесса с конечным числом состояний.

6. Концепция целостного компьютера и Synergonet.

 

Глава третья.

Параметр целого.

 

1.Выбор основной меры, характеризующей объект (параметра целого).

2. Простейшая форма математического описания объекта.

3. Эмпирический анализ двумерного фазового пространства, описываемого

параметром целого и скоростью его изменения или  некоторым итерационным процессом.

 

Глава четвёртая.

Комплексный параметр целого.

1.Комплексификация меры. Возможный физический смысл комплексификации.

2. Описание динамики структуры как линейного итерационного процесса.

3. Решение комплексного линейного дифференциального уравнение как предел системы линейных итераций.       

4. Введение экспоненциального времени. Степенные зависимости параметра целого от времени.

5. Алгебраические и спиральные комплексные числа.

6. Бифуркации экспоненты окружности.

7. Числа Абрама Моисеевича Басина

 

Глава пятая

Голоморфная динамика одной комплексной переменной.

 

1. Нелинейные  итерационные процессы с одной комплексной переменной.

2. Комплексный Гамильтоииан.

3 . Бифуркация рождения цикла в итерационном процессе.

4. Странный аттрактор итерационного процесса.

5. Первые представления о фрактальной геометрии.

 

Глава шестая

Описание структуры как динамической системы.

 

1.Принцип Хакена- Баранцева при выборе основных координат, описывающих систему.

2. Предварительное знакомство с тринитарной методологией.

3. Линейная система комплексных итерационных  соотношений. Сведение её к одномерной задаче.

4. Линейная теория комплексных дифференциальных уравнений.

5. Введение экспоненциального времени. Степенные зависимости  динамических переменных от времени.

6. Гамильтоновы  системы.

 

Глава седьмая.

Динамика бифуркаций.

 

1. Теория катастроф.

2 Числа А. М. Басина как бифуркационые параметры.

3. Бифуркация рождения цикла. Возникновение автоколебаний.

4. Сценарии перехода к странному аттрактору.

5. Основные свойства странных аттракторов.

6. Русла и джокеры Г  Г. Малинецкого.

 

Глава восьмая.

Резонансы в конечномерных динамических системах.

 

1. Классическое определение резонанса

2. Первичный лингвистический анализ слова резонанс.

3. Исследование частоты встречи слова резонанс в Internet.

4. Смысл, вкладываемый в слово резонанс различными авторами.

5. Простейшее дифференциальное уравнение, решение которого даёт представление о классическом резонансе.

6. Внутренние резонансы в системах линейных дифференциальных уравнений с конечным числом степеней свободы.

7. Параметрический  резонанс.

8. Нелинейные резонансы в динамических системах.

9. Нелинейные резонансы и автоколебания.

10.         Резонансы в системах, описываемых комплексными уравнениями.

11.         Резонансные явления при произвольных внешних воздействиях.

12.         О возможности степенных резонансов.

 

Часть вторая.

Синергетическая методология.

Линейные и нелинейные волны.

 

Глава первая..

Тринитарная методология Р. Г. Баранцева.

 

1. Диадное противопоставление противоположностей.

2. Линейные триады.

3. Гегелевские триады.

4. Целостные  триады.

 

Глава вторая.

Континуальные модели динамических систем.

 

1. Динамика твёрдого тела.

2. Динамика жидкости, газа и плазмы.

3. Квантовая динамика.

4. Теория относительности .

5. Квантовая теория поля.

 

Глава третья.

Классификация волн,  вихрей, структур и информационно-транспортных систем.

 

1. Классификация по принципу квант – волна.

2. Классификация по физическому принципу.

3. Классификация по степени нелинейности.

 

Глава четвертая.

Линейные волны.

 

1.Одномерное линейное волновое уравнение.

2.Трёхмерные линейные волновые уравнения.

3. Дисперсионные соотношения.

4. Линейные волновые резонансы.

 

Глава пятая.

Умеренно-нелинейные волны.

Солитоны.

 

1. История открытия солитонов.

2.Уравнение Кортевега – Де Фриза.

3. Солитонные решения уравнения Кортевега - Де Фриза.

4. Другие нелинейные уравнения, порождающие солитонные решения.

5. Алгебры Каца – Муди и их представления.

6. Взаимодействие солитонов.

 

Глава шестая.

Ударные волны.

 

1. Уравнение  простой волны.

2. Уравнение Бюргерса.

3. Формирование ударной волны.

4. Ударные волны  в трехмерном пространстве.

       5.  Комплексная супер - ударная волна

 

Глава седьмая.

Умеренно-нелинейные волны.

Границы раздела сред. Фазовые переходы.

 

1.Границы твёрдого тела

2. Границы раздела жидкостей и газов различной плотности.

3. Фазовые переходы.

4.Кристаллизация-плавление.

5.Конденсация – кипение

6. Кавитация.

7. Тройные точки

8. Границы раздела трёх сред.

9..Точка пересечения трёх границ, разделяющих четыре среды.

 

Глава восьмая.

Умеренно-нелинейные волны.

Режимы с обострением  С. П. Курдюмова.

 

1.Основные дифференциаиильные уравнения в частных производных, порождающие режимы с обострением.

2. Параметры режимов с обострением.

3. Взаимодействие режимов с обострением.

 

Глава девятая.

Автоволны.

 

1.Нелинейные уравнения, порождающие автоволны.

2. Математическое описание автоволн.

3. Взаимодействие автоволн.

 

 

Часть третья.

Вихри. Грибовидные  и древовидные структуры.

 

Глава первая.

Теория вихрей.

 

1. Математическое описание завихрённости.

2. Основные инварианты вихревых потоков.

3. Вихревая форма уравнений сплошной среды.

 

Глава вторая.

Вихревые ударные волны.

 

1.Пограничные слои.

2. Вихревые ударные волны первого рода. Двойные спиральные вихри.

3. Формирование  концентрированных вихрей.

4. Перезамыкание концентрированных вихрей.

5. Опрокидывание волн на границах раздела сред.

6.Перезамыкание пограничных слоёв.

7.Вихревые ударные волны второго рода. Скачки касательных скоростей.

8. Ревербераторы.

 

Глава третья.

Грибовидные структуры.

 

1.Определение грибовидной структуры как сложной нелинейной волны.

2. Способы формирования грибовидных структур.

3.  Поток около крыла как нейтральная грибовидная структура.

4. Проточная волна, связанная с грибовидной структурой. Её длина и период.

5. Циркуляционная волна, связанная с грибовидной структурой. Её длина и период.

6. Тело-волна, связанная с грибовидной структурой. Её длина и период.

7. Бифуркации грибовидных структур.

8. Полное и частичное размножение грибовидных структур.

 

Глава четвёртая.

Древовидные структуры.

 

1. Теория графов.

2. Математическая теория деревьев.

3. Формирование древовидных структур при неполном размножении грибовидных.

4. Основные свойства древовидных структур.

 

Глава пятая

Вихре - волновой и (или) структурный резонанс. История открытия.

 

1. Нелинейные резонансы поверхностных и внутренних волн в стратифицированной жидкости.

2. Результаты  теоретических и экспериментальных исследований  сил,  действующих на тела, движущиеся в ограниченном водоёме или обтекаемые ограниченным потоком.

3. Критические значения числа Фруда по длине тела и глубине жидкости.

4. Движение крыла вблизи границы раздела сред. Аномальные режимы обтекания. Результаты теоретических исследований.

5. Кавитационное обтекание крыла. Аномалии переходного режима.

6. Рождение концепции вихре - волнового и  (или) стуктурного резонанса.

 

Глава шестая

Концепция работает.

 

1. Основные параметры движущегося тела как уединённой волны.

2. Классификация вихре – волновых и (или) структурных резонансов.

3. Дисперсионные свойства сплошной среды.

4. Резонанс по скорости.

5. Околозвуковое и сверхзвуковое движение твёрдых тел.

6. Движение тела на мелководье.

7. Структурно - волновой резонанс по скорости и продольному размеру тела.

8. Основной безразмерный параметр вихре - волнового и (или) структурного резонанса.

9. Горб волнового сопротивления тел в ограниченном фарватере как результат резонансного взаимодействия второго класса.

10.         Резонансные явления при движении тел в стратифицированной жидкости.

11.         Вихре - волновой резонанс при движении крыла вблизи границы раздела сред.

12.         Качественный анализ нелинейных эффектов.

13.         Результаты экспериментального исследования проявлений вихре - волнового и (или) структурного резонанса.

14.         Вихре - волновой резонанс в стратифицированной сплошной среде. Теоретические  предсказания.

15.         Вихре - волновой резонанс в электродинамике движущихся сред.

16.         Движение крыла вблизи экрана как проявление четвёртой формы вихре – волнового и (или) структурного резонанса. Биологические и технические приложения.

17.         Качественный анализ кавитации крыла в режиме структурного резонанса.

18.         О возможности обнаружения новых  форм вихре – волнового и (или) структурного  резонанса.

 

 

Часть четвёртая.

Транспортно- информационные системы.

 

Глава первая.

Классификация транспортно -  информационных систем.

 

1. Основные сведения о взаимодействии структур и систем.

2. Статистические  закономерности в частоте встречи структур и систем с различными параметрами.

3. Граф структур и событий.

4. Понятие энтропии.

5.Понятие информации.

6. Триада структура-контроллер-поле.

7. Обобщённая концепция вихре – волнового и (или) структурного резонанса.

8. Классификация транспортно-информационных систем.

 

Глава вторая.

Термодинамические системы.

 

1. Кинетическая теория газов.

2. Теория плазмы.

3. Кинетическая теория жидкостей.

4. Основные законы термодинамики.

5. Физика твёрдого тела.

6. Динамика сплошной среды.

 

Глава третья.

Теория неравновесных   систем И. Р. Пригожина и Ю. Л. Климонтовича.

 

1. Принцип минимума роста энтропии.

2. Теория диссипативных систем.

3  Неравновесная термодинамика.

 

Глава четвёртая.

Энтаеросистемы Ю. К. Крылова.

 

1. Определение энтаеросистемы.

2. Иерархия масштабов и структур в энтаеросистеме.

3. Статистика распределения элементов в энтаеросистеме.

4. Теория самоорганизованной критичности.

5. Концепция идеального трансформера.

 

Глава пятая.

Сетевые транспортно – информационные системы.

 

1. Сетевые транспортные системы  грибовидных структур.

2. Основы  математической теории сетей.

3. Масштабная иерархия триад структура-контроллер-поле.

4. Эволюция основной системной триады.

5. Обобщённая концепция структурного резонанса.

6. Иерархия грибовидных и древовидных структур в сетевых транспортно-информационных системах.

7. Эволюция контроллеров транспортно- информационных систем.

8. Проблема появления сознания в транспортно-информационной системе.

 

Часть пятая.

Приложения  Синергетики.

 

Глава первая…………………………. 

Вселенная  как саморазвивающаяся система.

 

1. Рождение Вселенной .Теория Большого Взрыва

2. Рождение Галактик. «Блины» Я.Б. Зельдовича.

3. Формирование звёзд первого поколения.

4. Рождение звёзд второго поколения

5. Происхождение Солнечной системы.

6. История Земли

7. Зарождение  и эволюция жизни

8. Происхождение человека.

 

Глава вторая.

О структуре человечества как сложной самоорганизующейся системы.

 

1. Параметр целого

2. Основная системная триада, описывающая человечество.

3. Построение системы триад.

4.Параметры дифференциации людей как квантов системы человечества.

5.Динамика распределения населения по поверхности Земли.

6.Исслеование влияния границ и переходных зон на структурообразование.

 

Глава третья.

Сопоставление математических моделей, описывающих динамику человеческого общества.

 

1.Динамика комплексного  параметра целого.

2.Основные характеристики человечества как волны.

3.Динамика человеческого общества. Качественный анализ.

4.Путь в Synergonet.

 

Глава четвёртая

Синергетика. Взаимодействие с другими дисциплинами.

 

1. Синергетика и математика.

2. Синергетика и философия.

3. Синергетика и искусство.

4. Синергетика и конкретные науки..

 

Заключение

Основные нерешённые проблемы

    

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Басин М. А., Шилович И. И

 

Синергетика. Её особенности как науки.

 

Синергетика может стать новой парадигмой Internet, так как она изначально по самой своей идее является средством качественно нового объединения усилий не только всей современной науки, но и всех культурных достижений че-ловечества. Здесь очень уместны слова Р. Г. Баранцева: «На  сей раз человечество подошло к рубежу, на котором одномерное антагонистическое мышление становится самоубийственным. В рамках такого мышления невозможно примирить тенденцию к взаимозависимости и суверенности частей современного мира. Совместить единство целого и свободу частей удается лишь в мягкой структуре, обладающей свойствами открытой системы. В жесткой структуре единение ведет к тоталитаризму» [1].

 Отметим также утверждение одного из главных родителей синергетики - Германа Хакена: «Одна из принципиальных задач  синергетики - научиться эффективно хранить, перерабатывать, передавать и использовать большие информационные потоки» [2]

В науке возникло мощное, быстро развивающееся интеграционное направление - синергетика (synergetics), позволяющее обобщать знания, накопленные человечеством, и использовать новые методы, которые одинаково хорошо применимы как в естественных науках, так и в науках о человеке и человеческом обществе. Именно развитие синергетики, по нашему мнению, позволит создать принципиально новые методы существенного сжатия больших массивов информации. И главное - это не просто сжатие, а появление нового смысла - нового знания.

В средствах массовой информации появилось новое дитя научной и информационной революции - Internet - международная информационная сеть, связывающая компьютеры всего мира.

Эти два направления информационного потока, будучи синергетически объединены, могут стать основой информационной системы человечества XXI в.

 Это фундаментальное положение стало основой дипольной структуры методики наших исследований. Не случайно как синергетика, так и Internet появились в те же 80-е годы, которые мы считаем началом ноосферы. Не случайно один из этапов введения слова «синергетика» в научный обиход связан с первыми пользователями вычислительных машин [6].

Остановимся на этих важнейших проявлениях качественных изменений в информационной координате человеческого общества более подробно.

 

Если классифицировать решаемые наукой задачи по степени сложности, то можно сослаться на Дж. Клира [5]. Он отнес достижения Ньютона с его мощными упрощениями и развитие этих достижений в виде теории относительности квантовой механики к задачам организованной простоты. Л.Больцман и Дж. Гиббс создали статистические методы, получившие название задач неорганизованной сложности.

Это две крайности, между ними оказались задачи с резонансными свойствами системной организованности. Бурное развитие нелинейных методов исследования сложных систем и сделанные в процессе этого развития открытия привели к тому, что ученые различных специальностей вновь почувствовали необходимость в обобщении и синтезе потока новых знаний и отыскании общих закономерностей развития сложных систем, способных к самоорганизации. Возникшую при этом междисциплинарную науку выдающийся немецкий ученый Герман Хакен назвал красивым именем «синергетика».

Глубокий анализ начального состояния развития синергетики дали два российских ученых: Ю.А.Данилов - не только блестящий физик, но и замечательный педагог и популяризатор последних научных достижений, благодаря усилиям которого российские читатели познакомились с последними достижениями лучших представителей мировой науки, и Б. Б. Кадомцев - один из крупнейших специалистов в области термоядерной физики [6].

Термин «синергетика» происходит от греческого «synergeia» -содействие, сотрудничество. Более часто встречающимся до последнего времени было слово «синергизм»:

1) совместное функционирование органов и систем;

 2) комбинированное действие лекарственных веществ на организм, при котором суммарный эффект превышает сумму воздействий, оказываемых каждым компонентом в отдельности. Слово «синергетика» также употреблялось еще до Г.Хакена. Ч.Шеррингтон называл синергетическим согласованное воздействие спинного мозга в процессе управления мышечными движениями.

С. Улам был непосредственным участником одного из первых численных экспериментов на ЭВМ. Расчеты численного аналога системы кубических осцилляторов привели к неожиданному результату, породившему знаменитую проблему Ферми – Паста - Улама: проследив за эволюцией распределения энергии по степеням свободы, авторы не

обнаружили ни малейшей тенденции к равномерному распределению. С. Улам понял всю важность и пользу «синергии, т. е. непрерывного сотрудничества между машиной и ее оператором» [7]. Решение проблемы Ферми-Паста-Улама было получено в начале 60-х годов М. Крускалом и Н. Забусским, доказавшими, что исследуемая математическая задача представляет собой конечно-разностный аналог нелинейного волнового уравнения Кортевега де Вриза, решением которого является уединенная волна - солитон (термин, предложенный Н. Забусским). Понимая ограниченность аналитического и численного подхода к решению существенно нелинейных задач, Н.Забусский предложил единый «синергетический подход к нелинейным математическим и физическим задачам». По его словам, этот подход «можно определить как совместное использование обычного анализа и численной машинной математики для получения решений разумно поставленных вопросов математического и физического содержания системы уравнений» [8].

Что же такое синергетика Г. Хакена? Очень сжато и четко сформулировал триаду элементов, формирующих синергетику, выдающийся Санкт-петербургский механик и философ Р. Г. Баранцев [9] –

 

            нелинейность-когерентность-открытость.

 

Эти три элемента присутствуют во всех определениях синергетики, данных различными авторами, хотя мы согласны с мнением Л. И. Мандельштама [10, 11], поддержанным Ю.А.Даниловым и Б. Б. Кадомцевым [6], о ненужности строгих определений нелинейной науки (синергетики) на этапе ее развития.

Посмотрите, как расширяют наши представления о синергетике некоторые определения.

Хакен Г.:

Синергетика - теория «совместного действия многих подсистем, в результате которого на макроскопическом уровне возникают структура и соответствующее функционирование» [12]-

(когерентность).

«...Базовые понятия синергетики, такие как неустойчивость, параметры порядка и принцип подчинения» [13]

(нелинейность).

«...Процесс обмена информацией, ее производство, передачу и прием с обработкой и возникновением - саморождением новых качеств и нового смысла - называем синергетикой» [14]

(открытость).

 

Пригожин И.:

 «Переход в неравновесное состояние пробуждает независимые ранее частицы и устанавливает когерентность, совершенно чуждую их поведению в равновесных условиях» [15]

(нелинейность и когерентность).

 

Капица С. П., Курдюмов С. П., Малинецкий Г.  Г.: «Синергетика представляется нам не догмой и даже не руководством к действию, а способом взглянуть на проблему, который иногда оказывается полезен по существу. Хотя, конечно, форму, моду и обаяние тех людей, которые занимаются синергетикой, нельзя сбрасывать со счетов» [3] (открытость как систем, так и методов).

 

Курдюмов С. П. и др.:

«Синергетика - это не инструмент, дающий предзаданные результаты, а дверь, открытая в реальность, природную и человеческую, и ожидающая ответов от самой этой реальности» [16]

(открытость).

 

Трофимова И. Н.:

«Синергетику часто называют наукой о сложном, наукой о самоорганизации. Можно было бы ее назвать наукой об эволюции: она анализирует универсальные закономерности развития сложных динамических систем, изменение состояния системы в условиях ее взаимодействия со средой» [17]

(открытость, нелинейность).

 

Данилов Ю.А., Кадомцев Б. Б.:

 «...Название еще не сложившегося окончательно научного направления, занимающегося исследованием процессов самоорганизации и образования, поддержания и распада структур в системах самой различной природы (физических, химических, биологических и т. д.)» [б].

 

По мнению этих же авторов, «в отличие от большинства новых наук, возникавших, как правило, на стыке двух ранее существовавших и характеризуемых проникновением метода одной науки в предмет другой, (она) возникает, опираясь не на граничные, а на внутренние точки различных наук, с которыми она имеет ненулевые пересечения; в изучаемых (ею) системах, режимах и состояниях физик, биолог, химик и математик видят свой материал, и каждый из них, применяя методы своей науки, обогащает общий запас (её) идей и методов».

Синергетика –это наука о «чёрных лебедях» в соответствии с монографией []

 

 

 Основные достижения в различных областях знаний, ставшие основой синергетики

 

Вбирая в себя все последние достижения математики, нелинейной физики, химии, биологии, наук о Земле, синергетика обнаружила существование в сложных системах различной природы универсальных качественных закономерностей возникновения, развития и разрушения новых структур. Обобщение эмпирических данных и нахождение соответствия их с данными теории позволяет не только получать новые результаты в механике (в частности, в гидродинамике), физике, химии, но и сделать первые попытки применения новых методов и результатов в биологии, социологии, языкознании и гуманитарных науках. Перечислим основные общепризнанные открытия, которые в последние годы были сделаны в математике и естественных науках и в настоящее время используются на практике.

1. Создание  Уитни теории особенностей гладких отображений и классификация этих особенностей. Эти результаты были затем положены Р. Томом, В. И. Арнольдом и другими учеными в основу математической теории катастроф [18-22] и использованы для классификации особенностей, аттракторов и бифуркаций фазового пространства динамических систем. Классификация была начата А. Пуанкаре и продолжена большой группой исследователей, среди которых значительное место занимают ученики Л. И. Мандельштама, в частности нижегородская группа исследователей, возглавлявшаяся А. А.Андроновым. Эта достаточно интенсивно развивающаяся в настоящее время математическая теория находит все большее применение в различных областях знания и взята на вооружение синергетикой.

2. Открытие Лоренцем нового типа аттрактора (странного), который был обнаружен им при решении задачи о тепловой конвекции атмосферы в достаточно простой системе нелинейных дифференциальных уравнений, что положило начало большому количеству работ как в направлении усовершенствования классификации аттракторов динамических систем, так и в исследованиях перехода ламинарных течений жидкости в турбулентные [23].

3. Открытие нового универсального трансцендентного числа - числа Фейгенбаума, характеризующего последовательные бифуркации однопараметрических динамических систем, приводящие к странному аттрактору [23].

4. Введение Б. Мандельбротом понятия фрактальной геометрии и установление связи фрактальности с теорией комплексных нелинейных отображений, странными аттракторами, границами областей, фазовыми переходами и переходами типа порядок-хаос [24, 25]. В 1993г. было сделано сенсационное открытие фрактальной природы сетевых графиков, практически использованное в Internet [26].

5. Новые достижения в теории динамических систем с мерой, связанные с именами А. Н. Колмогорова, Я. Г. Синая и ряда других исследователей [27, 28], которые позволили по-новому взглянуть на понятия энтропии и информации.

6. Разработка школой И.Р.Пригожина и Ю.Л. Климонтовичем основных положений неравновесной термодинамики и получение принципиально новых научных результатов, приведших к более глубокому пониманию второго закона термодинамики и даже к новому представлению о понятии времени [15, 29-31].

7. Новый мощный всплеск в теоретическом и экспериментальном изучении солитонов и в практическом их использовании, а также обнаружение связи теории солитонов с квантовой теорией поля [32-34] и создание принципиально новых каналов передачи информации в Internet [35].

8. Открытие и изучение школой Н. Н. Самарского, С. П. Курдюмова новых закономерностей в нелинейной теории сплошных сред (в частности, в теории горения), связанных с так называемыми режимами с обострением [36-38].

9. Открытие и исследование российскими химиками и биофизиками автокаталитических реакций и автоволн в активных средах [39, 40].

10. Новое понимание соотношения в природных явлениях порядка и хаоса и изучение механизма их чередования при формировании структур [30, 41, 42].

11. Обнаруженное Г. Хакеном явление, связанное с тем, что самоорганизация сложных структур определяется в основном поведением одной - двух фазовых координат, названных им ведущими модами, или параметрами порядка [12].

 

12. Открытия, связанные с резонансным формированием вихре-волновых структур в океане, а также при взаимодействии движущихся тел с неоднородной сплошной средой [43-47]..Разработка Г. И. Басиной и М.А. Басиным принципиально новой классификации вихрей, волн, структур и информационно-транспортных систем [48-52].

13. Открытие новых статистических закономерностей в распреде-лении элементов и структур в сложных самоорганизующихся системах [53-76] и разработка новых методов качественного и количественного анализов динамики сложных информационно-транспортных систем [77, 78].

14. Принципиально новые результаты, связанные с применением синергетических методов в таких «гуманитарных» науках, как психология, история, культурология [3, 16, 79-82].

16. Мощные философские обобщения, базирующиеся на синергетических принципах[1, 83-84], в частности. создание семиодинамики и  тринитарной парадигмы Р.Г. Баранцева.

Повторяем, следуя [6], то, что еще в тридцатых годах нашего века Л. И. Мандельштам сформулировал программу выработки «нелинейной культуры, включающей надежный математический аппарат и физические представления, адекватные новым задачам, нелинейную интуицию, годную там, где оказывается непригодной интуиция, выработанная на линейных задачах» [10, 11]. Разработанная почти век назад, эта программа стала особенно актуальной в наши дни. Без наглядных и ёмких визуальных и словесных образов, адекватных нелинейному математическому аппарату, немыслимо успешное построение динамики взаимодействия структур и систем - теории существенно нелинейной.

Значительный вклад в развитие синергетических исследований внесли и санкт-петербургские ученые. С мая 1993 г. по инициативе выдающегося ученого и общественного деятеля В. Д. Поремского в Санкт - Петербурге работает семинар «Синергетика и методы науки», возглавляемый М. А. Басиным, а с октября 1995г. - научно-исследовательский центр «Синергетика». В организации семинара и центра активную роль сыграли Санкт-Петербургский научный центр РАН и Санкт-Петербургский союз ученых. Вышли в свет сборник докладов проведенного центром «Синергетика» круглого стола «Синергетика и психология» [79], сборник трудов семинара «Синергетика и методы науки» (издание поддержано грантом РФФИ № 97-06-87108). В 1996г. в Москве также по инициативе В.Д. Поремского был организован Московский международный синергетический форум, на котором выступили десять санкт-петербургских ученых [85, 86].

 

3. Internet о Синергетике.

 

Возникает вопрос: какова может быть связь между синергетикой и Internet? Можно представить себе триаду элементов взаимодействия.

1. Использование Internet для хранения и распространения информации о достижениях синергетических исследований с последующей оценкой состояния ее развития и определения границ.

2. Использование синергетических методов для качественного и количественного анализа Internet как самоорганизующейся транспортно-информационной системы

3. Осуществление синергии в смысле Улама—Забусского с целью построения коллективного интеллекта человечества, вступившего в эпоху ноосферы, - создание принципиально новой структуры, названной нами synergonet.

Обратившись в 1998 году Internet с ключевыми словами synergetics theory, М. А. Басин и И. И. Шилович получили около трехсот публикаций, начинающихся с 1952г. Другие виды поиска отчетливо обозначили прагматическое стремление авторов и созданных специализированных фирм (например, «Synergetics Incorporated») к реализации механизма синергетики для решения разнообразных практических задач, в том числе синергетического анализа комплексных систем. В 80-е годы Г.Хакен формулирует основные принципы конструирования синергетического компьютера, в 1991 г. публикует алгоритм его построения [14], а в 1997г. получает патент на синергетический компьютер. Возможность ознакомиться с обобщенным приложением синергетических принципов во многих областях мировой науки с конкретными приложениями использования синергетического компьютера и его патентованием в различных странах нам с профессиональным блеском предоставил Н.П. Лиходедов - руководитель Петербургского отделения информационной системы и компании LEXIS-NEXIS, он же - соавтор написанной им совместно с Л.Е.Товстых увлекательной и доступной книги о профессиональных базах данных и методологии решения проблемы «от научной идеи - к рынку» [87].

Развитие синергетики в России и странах СНГ было представлено в Internet уже несколькими десятками адресов из разных городов, включающих научно-исследовательские и учебные институты и отдельных ученых. Сообщается в Internet также и об издании в России новых книг по синергетике. Необходимо отметить, что проводившийся еще полгода назад аналогичный поиск практически не дал результатов.

 

Прошло 15 лет.

 

Картина кардинально изменилась.

 

Одним из предшественников синергетических исследований, имя которого редко упоминается при написании истории ее возникновения, по нашему мнению, является Альфред Норт Уайтхед (1861-1947). Он оставил о себе память не только работами в области математики и философии, но и последующим резонансом - в десятках монографий, сотнях статей и диссертаций обсуждаются его идеи. В специально издаваемом журнале «Исследование процесса» (Process Studies) и его приложениях развивается методологический подход Уайтхеда. Чтобы не исказить своей трактовкой идеи Уайтхеда, предоставим слово автору:

«Первейшим правилом научной методологии является. требование формулировать наблюдаемые соотношения наблюдаемых фактов. В этом состоит смысл знаменитого учения Бэкона: „наблюдай и наблюдай, пока не обнаружишь регулярность в последовательности фактов". Для понимания гармонии и дисгармонии существенно помнить о том, что сфера и интенсивность опыта зависят от субстрата тех элементов, из которых состоят значимые индивидуальные объекты. Видимость складывается удачно, если она упрощает хаотическую совокупность индивидуально незначительных событий и превращает ее в небольшое число значимых индивидуальных вещей. Самосознание отличает только конечный результат процесса, но не начальные стадии его, т. е. не охватывает генезис. Так и возникает бифуркация, раздвоение. Парадигма становления действительного происшествия, которое необходимо выполнить, когда начинается абстрактно-аналитическое рассуждение о „схватываниях" и „структурах". Структурные связи являются объективным коррелятором законов науки. Природа являет себя нам как становление, любой ограниченный процесс природы, сохраняющий присущую всей природе конкретность описания, представляет собой становление, его-то я и называю событием. Я даю имя „occation" пространственно-временному происшествию» [88].

Разрабатываемая авторами теория взаимодействия структур и систем позволяет представить динамику сложной системы в виде графа событий, происходящих с объектами, включенными в систему. Под событием понимается промежуток времени, в процессе которого происходят качественные изменения тех или иных объектов, входящих в систему, или всей системы в целом. Одной из основных координат события является время, в течение которого оно происходит (или с определенной вероятностью могло бы произойти, если речь идет о будущих или прошлых событиях). Граф, описывающий динамику выделенной системы, кроме временной координаты имеет еще две составляющие: бифуркационную, выражающуюся в отсутствии полной определенности как прошлого, так и будущего исследуемой системы, и объектную - характеризующую типы (классификацию) и меры (значимость) объектов, входящих в систему и взаимодействующих между собой.. При этом объектная составляющая представлена в виде двух координат: класса (типа) объекта (а) и его значимости - величины соответствующей ему обобщенной меры.

Такое расщепление объектной обобщенной координаты отражает в какой-то мере системологическую парадигму оценки современной науки - ее двумерность (и даже трехмерность), представленную Клиром [5]. Классическая наука (science) изучала в основном динамику мер, т. е. количественные параметры, характеризующие объекты. Классификация объектов по их типам, а следовательно и взаимодействие объектов различных классов, во многих случаях либо игнорировались, либо осуществлялись вне сферы научных исследований (несколько по-иному обстояло дело в биологии и гуманитарных науках). С развитием системных исследований все большую роль стали играть классификационные принципы. Исследование свойств систем стало наукой о свойствах отношений между элементами различных классов. Появилось второе измерение науки - классификация элементов систем различной природы и взаимоотношений этих элементов.

Это принципиальное отличие двумерной (многомерной) науки особенно ярко представлено в нелинейных неравновесных информационно-транспортных системах, состоящих из большого числа элементов, в которых намечается еще одна координата - иерархия масштабов ветвей графа, проявляющаяся, например, в принципиальном различии микро- и макромира, в волновых движениях, в материальных объектах, в масштабной иерархии элементов и подструктур. Именно наличие иерархии масштабов родило основные представления фрактальной геометрии, пронизывающей всю синергетику и всю Internet.

Успех «Постижения истории» А.Тойнби [89] и глубина его постижения обусловлены убедительным показом двумерности развития цивилизаций. Одно измерение содержит классификацию цивилизаций по типам (двадцать одна цивилизация). Главный аспект второго измерения - динамика обобщенных координат - состояния обществ данного типа (рост, надлом, распад).

Предложенная одним из авторов классификация волн, вихревых, грибовидных структур и транспортно-информационных систем (интаэросистем, по определению Ю.К.Крылова [76]), изложена в статьях [48-52],

 

Основной целью этих работ явилось создание такой единой классификации волн, вихрей, структур и систем, в рамках которой удалось бы проследить за характером влияния нелинейности на переход классических линейных волновых движений в динамические структуры и сложные самоорганизующиеся системы.

 Вот что пишет об этом А.Тойнби [89]: «Воображение не проводит четкой линии между двумя эпохами мировой истории. Скорее оно порождает движение волны мимесиса, и эта психическая волна движется наподобие других волн в других средах, она распространяется в различных направлениях из точки своего возникновения; ей требуется время для перемещения в пространстве, и, перемещаясь, она принимает разную длину, что зависит от местных условий и препятствий на ее пути» (мимесис - mimesis - подражательный, переимчивый). Волну, которую также целесообразно отнести ко второму классу, можно обнаружить и при анализе распространения Internet по земному шару.

Слова Н.Н.Моисеева, взятые нами в качестве эпиграфа : «Вся

картина мирового развития представляется как единый процесс турбу-лентообразного движения с разными временными и пространственными характеристиками (если угодно, хаотическим переплетением;

его вихреподобных образований» [90]. (На наличие этой корреляции нам любезно указал Р. Г. Баранцев).

Таким образом, изучение сложных систем в объектно-временной проекции может быть осуществлено в трехмерном (и даже четырех-мерном) пространстве, одной из осей которого является ось времени, объектное подпространство которого двух-, трехмерно, что отражает отмеченную системологией многомерность современной науки.

Элементами такого изучения являются объекты и события. Объекты можно сопоставить с линиями объектной проекции графа взаимодействия, а события - с узлами той же проекции графа.

База данных о той или иной системе взаимодействующих между собой объектов должна представлять справочник, построенный по аналогии с описанным графом, в котором в хронологическом порядке и в порядке значимости содержится информация об объектах, входящих в систему, и событиях, происходящих с этими объектами.

Однако построению такой базы знаний, как справочник, должна предшествовать кропотливая работа, проведенная с самой системой Interne t как с единым объектом.

=Это большая сложная транспортно-информационная система из грибовидных (дипольных) структур, шляпка каждой из которых (собственно диполи) представляет собой мозг человека, сидящего за компьютером, в совокупности с самим компьютером, который как бы является искусственным продолжением мозга, а ножки - например, телефонная сеть, соединяющая компьютеры, или эфир, через который передаются радиоволны. В отличие от многих других объектов природы Internet является уникальным объектом, что создает дополнительные сложности в ее исследовании. Однако в ней можно обнаружить многие черты, общие для всех информационно-транспортных систем, что позволяет осуществлять не только эмпирические исследования - мониторинг сети, но и разрабатывать теоретические модели Internet - по аналогии с близкими моделями для других транспортно-информационных систем.             

 

                                         

                                         

 

 

 

ЛИТЕРАТУРА

1. Баранцев Р. Г. Открытым системам — открытые методы // Синергетика и методы науки. СПб.: Наука, 1998. С. 438.

2. Хакен Г. Информация и самоорганизация. М.: Мир, 1985. (4-й том в шприн-геровской серии книг по синергетике http://link.springer.de/ol/total/sist.htm).

3. Капица С. П., Курдюмов С. П., Малинецкий Г. Г. Синергетика и прогнозы будущего. М.: Наука, 1997. 288 с.

4. Дульнев Г. Н. Введение в синергетику. СПб.: Проспект, 1998. С. 106—110.

5. Дж. Клир. Системология. Автоматизация решения системных задач. М.:

Радио и связь, 1990.

6. Данилов Ю. А., Кадомцев Б. Б. Что такое синергетика? // Нелинейные волны. Самоорганизация. М.: Наука, 1983. С. 5—16.

7. Улам С. Нерешенные математические задачи. М.: Наука, 1964. 161 с.

8. Nonlinear partial differential equations. N.-Y.: Acad. press, 1967. P. 223.

9. Баранцев Р. Г. Синергетика на фоне научных школ // Академические научные школы Санкт-Петербурга. К 275-летию Академии наук. СПб., 1998.

10. Мандельштам Л. И. Лекции по колебаниям. М.: Изд-во АН СССР, 1955. 503 с.

11. Гапонов-Грехов А. В., Рабинович М. И. Л. И. Мандельштам и современная теория нелинейных колебаний и волн // УФН. 1979. Т. 128, № 4. С. 579—624. 12 Хакен Г. Синергетика. М.: Мир, 1980. 414 с.

13. Хакен Г. Синергетика мозга//Синергетика и психология. Тексты. Вып. 1:

Методологические вопросы / Под ред. И. Н. Трофимовой и В. Г. Буданова. МГСУ Союз, 1997. С. 35.

14. Haken H. Synergetic Computers and Recognition. Berlin: Springer Verlag, P. 56-59.

15. Николис Г., Пригожий И. Самоорганизация в неравновесных системах. М.:

Мир, 1977. 512с.

16. Курдюмов С. П. и др. Социологический подход к прогнозированию социально-психологических явлений // Синергетика и психология / Под ред. М. А. Басина, С. В. Харитонова. СПб.: Изд. СПбУВК, 1997. 148 с. (Матер, круглого стола, 10031997).

17. Синергетика и психология. Тексты. Вып. 1: Методологические вопросы / Под ред. И. Н. Трофимовой и В. Г. Буданова. М.: Издательство МГСУ «Союз», 1997. С. 7.

18. Thorn R. (-'equivalence d'une fonction differentiable et d'un polynome // Topolo¬gy. 1965. N 2. S. 297—307.

19. Thorn R. Topological Models in Biology//Topology. 1969. N 3. P. 313—335.

20. Thorn R., Arnold V., Smale S. Dynamical Systems and Differential Equations // Mathematical developments arising from Hilbert Problems. Providense, Rl: Amer. Math. Soc., 1976, P. 59—62.

21. Арнольд В. И., ВарченкоА. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений. Классификация критических точек, каустик и волновых фронтов. М.: Наука, 1982. 304 с.

22. Арнольд В. И. Избранное 60. М.: Фазис, 1997. 768 с.

23. Странные аттракторы. Математика. Новое в зарубежной науке / Под ред. А. Н. Колмогорова и С. П. Новикова. М.: Мир, 1981. 256 с. (Сб. статей.).

24. Mandelbrot В. The Fractal Geometry of Nature. San-Francisco: Freeman, 1982.

25. ПейтгенХ.-О., Рихтер П. X. Красота фракталов. Образы комплексных динамических систем. М.: Мир,1993.176 с.

26. Открытие фрактальной природы сетевых графиков // Компьютер УИК-Моск-ва.1997. № 19.

27. КОЛМОГОРОВ А. Н. Основные понятия теории вероятностей. М.: Наука, 1974.

28. КорнфельдЛ. П., Синай Я. Г., Фомин С. В. Эргодическая теория М • Наука 1980.384с.

29. Гленсдорф П., Пригожий И. Термодинамическая теория структуры, устой¬чивости и флуктуаций. М.: Мир, 1973. 280 с.

30. Пригожий И., Стенгерс И. Время, хаос, квант. М., 1994. 272 с.

31. Климонтович Ю. Л. Статистическая теория открытых систем Т 1 М • Янус 1995.624с.

32. Сретенский Л. Н. Теория волновых движений жидкости М • Наука 1977 816с.

33. Абловиц М., СигурХ. Солитоны и метод обратной задачи М • Мир 1987 480с.

34. НьюэллА. Солитоны в математике и физике. М.: Мир, 1989. 328 с.

35. Бруске К. На смену оптоволокну идут солитонные каналы // Computer World Россия. 2121997.

36. Курдюмов С. П., Куркина Е. С., Потапов А. Б., Самарский А. А. Сложные многомерные структуры горения нелинейной среды //Журн. вычисл. матем. и ма-тем. физики. 1986. Т. 26, № 8. С. 1189—1205.

37. Самарский А. А., Галактионов В. А., Курдюмов С. П., Михайлов А. П. Режи¬мы с обострением в задачах для квазилинейных параболических уравнений М • Наука, 1987.

38. Курдюмов С. П., Малинецкий Г. Г., Потапов А. Б. Нестационарные структу¬ры, динамический хаос, клеточные автоматы // Новоеm в синергетике: Загадки мира неравновесных структур. М.: Наука, 1996. С. 95—165.

39. Васильев В. А., Романовский Ю. М., Яхно В. Г. Автоволновые процессы в распределенных кинетических системах // УФН. 1979. Т. 128, № 4. С. 579—624.

40. Васильев В. А., Романовский Ю. М., Яхно В. Г. Автоволновые процессы М • Наука, 1987. 240с.

41. Chaos and Order in Nature/Ed, by H. Haken. 1981.

42. БасинМ.А. О влиянии нелинейности и диссипации на формирование структур. Докл. на Втором Междун. философ.-культурол. симп.: «Размышления о хаосе». 18 апреля 1997 г.

43. Муравьев С. С., Озмидов Р. В. Синергетические механизмы образования упорядоченных структур в океане // Океанология. 1994. Т. 34, № 3. С. 325—336.

44. Basin M. A. Basic Equations of Vortex Fluid Motion. Vortex-Wave Resonance // IUTAM Symposium on Separated Flows and Jets, Novosibirsk: USSR, 1990. Springer-Verlag. Berlin—Heidelberg, 1990. P. 113—116.

45. Basin M. A. Wave Formation by the Motion of a Surface Ship Hedrodynamic Complex near the Free Boundary. Classification of Nonlinear Waves. Wave-Vortex Resonance // Proceedings of the VI Congress of the IMAM / Ed. Peter A. Bogdanov Varna 1993 Vol. II. P. 15—20.

 ////

46. Basin M. A. Vortex-wave Resonance in Hydrofoil Hydrodynamics // International Symposium on Ship Hedrodynamics Devoted to 85-th Anniversary of Birthday of Abram M. Basin (ISSH). St. Petersburg, 1995. P. 399-407.

47. Басин M. А. Вихре-волновой резонанс // Синергетика и методы науки / Под ред. M. А. Басина. СПб.: Наука, 1998. С. 415-^18.

48. Басин M. А. Основы классификации нелинейных волновых движений и вихревых структур. Явление вихреволнового резонанса при движении несимметричных тел в неоднородной жидкости // Проблемы гидромеханики в освоении океана. Киев: ИГМАНУ, 1992. (Матер, конф. по прикл. гидромех.).

49. Basin M. A. Foundations of Nonlinear Waves and Vortex Structures Classification. Paper, presented on the International Symposium: «Nonlinear Oscillations, Waves and Vortexes in Fluids». St. Petersburg, June, 1994. P. 192—193.

50. Basin M. A. Wave Methods in the Investigations of Structures and Systems. Moscow Forum of Synergetics, the January 1996 Meeting «The Sustainable Development in Changing World», January 27—31, Moscow: Abstracts. P. 36—38.m

51. Басин M. А. Основы классификации нелинейных волновых движений, вихрей и транспортных систем // Синергетика и методы науки. СПб.: Наука, 1998. С. 95—111.

52. Басин М. А. Синергетика — волновой подход к исследованию открытых структур и систем. Проблемы ноосферы и устойчивого развития. Матер. Первой Междун. конф. С.-Петербург, 9—15 сентября 1996 г. СПб.: Изд-во СПбГУ, 1996. С. 104—107.

53. Zipf G. К. Human Behavior and the Principal of the Least Effort. Cambridge. Mass, Addison—Wesley Press, 1949.

54. Мандвльброт Б. Теория информации и психологическая теория частот слов // Математические методы в социальных науках, М., 1973. С. 326—337.

55. Мандельброт Б. О рекуррентном кодировании, ограничивающем влияние помех // Теория передачи сообщений. М.: ИЛ, 1957. С. 139—157.

56. Шрейдер Ю. А. О возможности теоретического вывода статистических за-кономерностей текста//Проблемы передачи информации. 1967. Вып. 1. С. 57—63.m

57. Арапов М. В., Шрейдер Ю. А. Классификации и ранговые распределения // НТИ. Сер. 2. 1977. № 11—12. С. 15—21.

58. Арапов М. В., Шрейдер Ю. А. Закон Ципфа и принцип диссимметрии систе¬мы: Семиотика и информатика. Вып. 10. 1978. С. 74—96.

59. ArapovM. V., Krylov Yu. К. Mathematical Models of Classification in Application for some Problems of Statistical Linguistics. Symposium: Computational Linguistics and Relaten Topics. P. 24—26, Tallin, 1980. (Summaries).

60. Крылов Ю. К. Об одной парадигме лингвостатистических распределений:

Лингвистика и статистическая лингвистика // Уч. зап. ТГУ. 1985. Вып. 711. С. 66—80. Тарту

61. Крылов Ю. К. К вопросу об объеме словаря случайной выборки и связного текста: Квантитативная лингвистика и автоматический анализ текста // Уч. зап. ТГУ. 1985. Вып. 711. С. 66-80.

62. Крылов Ю. К. Стационарная модель порождения связного текста: Квантита¬тивная лингвистика и автоматический анализ текстов //Уч. зап. ТГУ. 1987. Вып. 774. С. 81—102.

63. Трубников Б. А., Румынский И. А. Простейший вывод закона Ципфа—Кры¬лова для слов и возможность его «эволюционной интерпретации» //ДАН СССР. 1991. Т. 321, № 2. С. 270-275.

64. Bak P., Tang С., Wiesenfeld К. Self-organized Criticality // Physical Reviu A. 1988. Vol. 38, N 1. P. 364—374.

 

65. Bak P., Tang C., Creutz M. Self-organized criticality in the «Game of Life» // Na¬ture. Vol. 342. 14 December 1989. P. 780—782.

66. Bak P., Tang С. Earthquakes as a Self-organized Critical Phenomena // Journ. Geophys. Res. 1989. Vol. 94, N B11. P. 15635—15637.

67. Bak P., Flyvbjerg. Selforganization of Cellular Magnetic-domain Patterns // Phys. Rev. A. 1992. N 45. P. 2182—2200.

68. Bak P. Sneppen Physical Reviu Letters. A. 1993. Vol. 71. P. 4083.

69. Sornette F., Sornette D. Self-organized Criticality and Earthquakes // Europhys. Lett. 1989. 9 (3). Р. 197—202.

70. Pietronenm L., Tartalgia P., Zhang Y.-C. Theoretical Studies of Selforganized Criticality// Physics. A. 1991. N 173. P. 22-^4.

71. DharD., Ramaswamy R. Exactly Solved Model of Self-oganized Critical Pheno¬mena// Physical Rev. Lett. 1989. N 63. P. 1659—1662.

72. Подлазов А. В. Новые аспекты самоорганизованной критичности. ИПМ им. М. В. Келдыша РАН. Препринт № 86. 1995.

73. Малинецкий Г. Г., Потапов А. Б. Нелинейность. Новые проблемы, новые возможности // Новое в синергетике: загадки мира неравновесных структур. М.: Нау¬ка, 1996. С. 165—191.

74. Малинецкий Г. Г., Митин Н. А. Нелинейная динамика в проблеме безопаснос¬ти // Там же. С. 191—215.

75. Вечерний В. В., Письмак Ю. М., Ковалев О. В. Самоорганизующаяся критичность как проявление наиболее фундаментальных механизмов эволюционных процессов // Проблемы ноосферы и устойчивого развития. Материалы Первой Меж¬дународной конференции. СПб., 1996. С. 123—126.

76. Крылов Ю. К. Интаэрология и синергетика // Синергетика и методы науки / Под ред. М. А. Басина. СПб.: Наука, 1998. С. 77—94.

77. Басин М. А., Орлов С. Г. Теоретическое исследование свободной транс¬портной динамической системы // Там же. С. 95—111

78. Басин М. А. К теории идеального трансформера // Там же. С. 356—375.

79. Синергетика и психология: Материалы круглого стола. 10 марта 1997, С.-Пе-тербург. Доклады / Под ред. М.А. Басина, С. В.Харитонова. Изд-во СПбГУВК 1997 С. 148.

80. Шишкина Л. С. Язык как естественная модель становления целого // Синер¬гетика и методы науки / Под ред. М. А. Басина. СПб.: Наука, 1998. С. 260—277.

81. Василькова В. В., Яковлев И. П., Барыгин И. Н. Волновые процессы в об¬щественном развитии. Новосибирск, 1992.

82. Каган М. С. Синергетика и культурология // Синергетика и методы науки / Под ред. М. А. Басина. СПб.: Наука, 1998. С. 201—219.

83. Князева Е. Н., Курдюмов С. П. Законы эволюции и самоорганизации слож¬ных систем. М.:1994.

84. Каган М. С. Философия культуры. СПб.: ТОО ТК «Петрополис», 1996. 416 с.

85. Московский синергетический форум. Январская (1996) встреча: «Устойчивое развитие в изменяющемся мире». 27—31 января, 1996/Под ред. В. И.Аршино-ва, Е. Н. Князевой. М., 1996, 118с. (Тезисы),

86. Win (cp1251) http://www/iph.ras.ru/-mifs/

87. Лиходедов Н. П., Товстых Л. Е. Мировые информационные ресурсы для бизнесменов и специалистов. СПб., 1997. 84 с.

88. УайтхедА. Н. Избранные работы по философии. М.: Прогресс, 1990.

89. ТойнбиА. Дж. Постижение истории. М.: Прогресс, 1991. 732 с.

 

90. Моисеев Н. Н. Современный рационализм. М., 1995. С. 174.

91. Моисеев Н. Н. Математические задачи системного анализа. М.: Наука,

1QR1

1981

92. Моисеев Н. Н. Человек и биосфера: Опыт системного анализа и экспери¬менты с моделями. М.: Наука, 1985.

93. Советский энциклопедический словарь. М.: Советская энциклопедия, 1990.

94. Черняк Л. Доклад на конференции AIS (3-rd American Conference on Infor-mation Systems (текст в http://www.brint.com/)).

95. Gompute/-Weekly.1998.N26—27.

96. Гартнер Г. Технологии электронных знаний. COMPUTER WRLD Россия. 3 февраля 1998 г.

97. КолесовА. PC WEEK/RE. 1998. №34.

98. Чиновник В. PC WEEK/RE. 1998. № 32-33. С. 13.

99. Шилович И. И., Харитонов Л. А. Информационная модель истории ВМФ России // Информационно-методический сборник № 1. М.: ЦМВС, 1997.

100. Харитонов С. В. О синергетическом подходе к проблеме классификации психических потребностей // Синергетика и методы науки / Под ред. М. А. Басина. СПб.: Наука, 1998. С. 220—236.

101. Аракин В. Д., Выгодская 3. С., Ильина Н. Н. Англо-русский словарь. М.:

Русский язык, 1991. 607с.

102. ЦишангХ., ФогтЭ., Колдевай X.-Д. Поверхности и разрывные группы. М.:

Наука, 1988. 688с.

103. Lance L. Internet в настоящем и будущем. COMPUTER WEEKLY. 1998. № 17.

104. Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука, 1971.240с.

105. Клейнрок Л. Вычислительные системы с очередями. М.: Мир, 1970.

106. Дорошенко А. GPSS—язык и система моделирования систем. PCWEEK;

13 мая 1997 г.

107. Юл. Дж. Эд., Кендэл М. Дж. Теория статистики. 14-е изд. Пер. с англ. М.:

Госстатиздат, 1960. С. 121.

108. Мандат на 2001 год. Технологии для государства XXI века. Microsoft, 1998.

109. Толстяков А. Электронная нервная система. Зачем и как проводить реин-жениринг IT? Microsoft Consulting Services. Middle East, 1998.

110. Esther Dyson Release 2.0. New York: Broodway Books, 1997. P. 8.

111. Hamilton S. Inside Microsoft Research. Computer, January, 1998. P. 51. Mic¬rosoft. COMPUTER WEEKLY N 30. 1998.

112. BendaM. Shaping the Internet: the Dynamics. COMPUTER WEEKLY. 1998. N23.

113. Аршинов В. И., Данилов Ю. А., Тарасенко В. В. Методология сетевого мы¬шления: феномен самоорганизации / Онтология и эпистемология синергетики. М.:

Ин-т философии РАН, 1997. С. 101-117.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Материалы  50 Семинара: «Синергетика и методы науки»

Посвященного  80-летию со дня рождения  д.ф-м.н., профессора                                 Баранцева Рэма Георгиевича

и.

  50-летию научной деятельности д.т.н. профессора

Басина Михаила Абрамовича.

 

1.Barantsev Rem Georgievich .Curriculum vitae

 

NAME                             Barantsev Rem Georgievich

DATE OF BIRTH           October 2, 1931

PLACE OF BIRTH         Kirov,  USSR

HOME ADDRESS          pr. Nauki 16-1-69   (or  Box 159)

                                         St.-Petersburg  195256  Russia

PHONE                            +7 (812) 5356598

E-MAIL                           brem@mail.ru

PRESENT POSITION     Professor of the St.-Petersburg State University

OFFICE ADDRESS        Bibliothechnaya pl.2, Petrodvorets,

                                         St.-Petersburg 198904  Russia

OFFICE TEL.(FAX)        +7 (812) 4286989

EDUCATION                  Leningrad State University

                                          Student            1949-1954

                                          Post-graduate   1954-1957

EXPERIENCE                 St.-Petersburg (Leningrad) State University

                                         Assistant           1957-1959

                                         Docent              1959-1968

                                         Professor           1969-2015

DEGREES                       Candidate of Sci.        1957

                                         Doctor of Sci.             1966

PUBLICATIONS            The list of publications contains 460 items

                                         including 10 books and 5 teaching aids

SOME OF THEM           Some problems of gas-solid surface interaction //

                                         Progr. Aerosp. Sci., vol.13, Oxford e.a., 1972, 1-80.

                                         System triad of definition // Intern. Forum Inform.

                                         Document., M., 1982, v.7, No.1, 9-13.

                                         On singularities of the Tricomi problem solution by

                                         the Fourier method // Mixed Type Equations. Leipzig

                                         Teubner, 1986, 47-54.

                                         Asymptotic versus classical mathematics // Topics in                

                                         Math. Anal., Singapore e.a., 1989, 49-64.

                                         Ruβland – zwischen Ost und West? // Die Menschen-

                                         Rechte im interkulturellen Dialog. Frankfurt a/M e.a.

                                         Peter Lang, 1998, 125-140.

RESEARCH INTERESTS     Mathematical physics, asymptotic methods,

                                         semiodynamics, synergetics, trinitary philosophy.

VISITING                      Hungary -  1962, Poland - 1968, 1975, 1994, 2000, England - 1970, China - 1996, 2002, Germany - 1997, Czechia - 1997, 1998, 2000, Latvia – 2004.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Баранцев Рэм Георгиевич

 

2.Автография

 

    Биография – слово стареющее, поскольку, согласно В.И.Вернадскому, из биосферы нам предстоит подниматься в ноосферу. Однако переход этот не гарантирован, так что пусть пока будет автография.

    Родился  я  2 октября 1931 г. в г. Кирове (Вятке). Родители – из бедных крестьянских семей. Стараясь учиться, они сумели получить высшее образование. Мать стала учителем истории, отец – агрономом. Всю войну он прошёл в пехоте и демобилизовался в звании капитана. Но последствия контузии помешали ему перестроиться на мирную жизнь. Отказавшись выполнять партийное поручение по взиманию налогов с обедневших колхозников, он покончил с собой в ноябре 1946 года. Мать умерла в 1998 г., немного не дожив до 94 лет. Из семерых детей пятеро умерли рано, младший сын (брат Владимир) дожил до 2002 г. Третий сын, в моём лице, остался один и собирается дожить до 82 лет.

 Раннее детство прошло в сельской местности. Читать я научился в 4 года и довольно рано перешёл с детских книг на более серьёзные. В школу пошёл в пос. Юрья Кировской области. С началом войны мать решила переехать в деревню и оформилась директором семилетней школы в село Верходворье.  Мне было 10 лет, но детство скоропостижно кончалось. Жизнь в деревне и так полна всяческих забот, а тут ещё и вся мужская работа свалилась на женщин и детей. Похоронки приходили в вятские деревни пачками. Людей спасали земля и лес. Но чтобы выжить, приходилось трудиться непрестанно. В 7-м классе нас было 8 учеников: три парня и пять девок. Мы умещались на двух удлинённых партах в маленькой комнате. Я сидел на первой парте слева у окна, размораживая руками оконную наледь. Писали на самодельных тетрадях, изготовленных из всякой бросовой бумаги. Верходворье – моя малая родина, которая каждый год зовёт меня взглянуть на старые тополя, по которым мы лазали, на пустыри, где когда-то был кормивший нас огород, на лес, куда мы бегали за грибами и ягодами. На реке уже нет старой мельницы, а больница, стоявшая на крутом берегу, давно сгорела, и пожарище заросло кипреем и крапивой. Старые школьные здания разрушились, а новое пустует из-за нехватки детей, хотя само село ещё живо.

Чтобы продолжать обучение в 8-м классе, пришлось искать жильё в Юрье, и мать сняла для меня комнатку у Марины Федотовны, которая раньше работала с ней в школе завхозом. Это была мудрая одинокая пожилая женщина, положительно влиявшая на школьника, не сразу научившегося разумно распоряжаться свободой. Уроки я учил исправно, хотя иногда всё-таки бывали срывы из-за увлечения футболом и волейболом. Кроме учебников, штудировал словарь иностранных слов и, вспоминая отца, который почему-то сравнивал меня с Герценом, стал внимательно читать «Былое и думы». С учителями, считаю, повезло. Литературу вдохновенно преподавала Нина Ивановна, любившая особенно Тургенева. Математику хорошо вела Евгения Марковна, искренне переживавшая успехи и неудачи учеников. Обе они были молодыми, растущими, полными энтузиазма. По воскресеньям я ездил домой за картошкой и другими немудрёными деревенскими продуктами. От ст. Юрья до разъезда Мосинский поезд шёл минут сорок, а потом оставалось 3 км пешком. Обратно надо было идти ночью, сбиваясь зимой с занесённой снегом тропы и опасаясь в перелесках вполне реальных волков. Заканчивали Юрьянскую среднюю школу в 1949 году 19 учащихся: 7 парней и 12 девчат. Выпускных экзаменов было много, и готовились мы к ним основательно. Тему сочинения я выбрал почему-то не по русской литературе, а о комсомоле, чем очень огорчил Нину Ивановну и о чём всегда сожалею. Оценки по литературе и математике у претендентов на медали утверждались в Кирове, и результат пришлось довольно долго ждать. Тем временем мы переехали в село Верхокамье. Известие о золотой медали мама привезла в тот день, когда я окучивал картошку, чередуя это занятие с чтением романа И.А.Гончарова «Обрыв».

Получив документы, я поехал в Москву поступать в университет. Однако приём медалистов там уже был закончен, и я сходу рванул в Ленинград. Первую ночь в Ленинграде я провёл в коммунальной квартире у дальних родственников деревенских соседей. Спал в коридоре на стульях и, вставая, гремел какими-то тазами. Утром пришёл на 10-ю линию 33 и представил там свои документы. Мне назначили явиться вечером на коллоквиум. Я не знал, что это такое, а спросить побоялся. Подумал, что какое-то представление, и вместо подготовки пошёл по городу искать кинотеатры. Выйдя на Невский проспект, был разочарован его узостью. Вечером сказали, что коллоквиума не будет, так как Дмитрий Константинович занят. Меня временно поселили вместе с другими двадцатью абитуриентами в большой аудитории на третьем этаже левого крыла факультета. Там было хорошо: близко до занятий и до столовой. Но не надолго. В конце сентября нас перевели в общежитие на Охте. Сосед по комнате Рюрик Шерстников считал себя уже продвинутым математиком и относился ко мне, деревенщине, покровительственно. Приниженное состояние сопровождало меня всюду: на лекциях, которые я не успевал понимать; в городе, красота которого мне ещё не открылась; в компании ленинградских однокурсников, ведущих умные разговоры о неведомых мне математических премудростях. Туда ли я полез?!  Ведь думал же пойти на юридический или философский, и только облегчающая чистота математических решений перевесила мутную притягательность общественных наук. Но до чистоты предстояло ещё пробиваться, терпеливо осваивая высшие миры математики и культуры. Интуиция и упрямство удерживали на мат-мехе.

Подготовка к экзаменам состояла в том, чтобы понять изучаемый предмет как органическую частицу своего миропредставления, стать ответственным хозяином нового знания. И когда это было достигнуто, первая пятёрка не очень удивила. Догоняя процесс обучения, я, не сбавляя темпа, выстраивал собственное здание, композиция которого прояснялась по ходу дела, вселяя уверенность, освобождённую от комплекса неполноценности. Ко мне стали обращаться за помощью в трудных местах, и это становилось нормальным. Подобное превращение хорошо описал мой земляк Олег Куваев в повести «Территория». Сосредоточившись на учёбе, я не успевал следить за театральными премьерами, посещать знаменитые музеи, участвовать в художественной самодеятельности. Зато в спорте достиг второго разряда по лыжам и третьего по шахматам, баскетболу, лёгкой атлетике. В комсомольском бюро факультета на мне был спортивный сектор, и в суете соревнований я расширял круг общения, избавляясь от замкнутости. Быт общежития тоже вносил свой вклад в роскошь человеческого общения. С Охты ходил тогда трамвай №4 аж по Невскому проспекту. Потом были общежития на 5-й линии, Мытнинской наб., пр. Добролюбова.

Учёба вошла в нормальную рабочую колею, и я исправно записывал лекции, решал задачки, посещал библиотеки. Экзамены сдавал на пятёрки и какое-то время был даже ньютоновским стипендиатом. Александр Данилович Александров, Сергей Васильевич Валландер, Соломон Григорьевич Михлин, Исидор Павлович Натансон, Владимир Иванович Смирнов, Дмитрий Константинович Фаддеев, Николай Александрович Шанин навсегда останутся в моей памяти теми профессорами, которые олицетворяют стиль и уровень университетского образования. На 4-м курсе Лев Васильевич Овсянников начал читать нам лекции по трансзвуковой газодинамике. Я взял у него тему курсовой работы, но он вскоре уехал в закрытый ядерный центр, а лекции дочитывал Игорь Леонидович Кароль. Мою курсовую он оценил на уровне дипломной. Эту работу я продолжил и защитил на 5-м курсе. Она стала моей первой научной публикацией.

Будучи рекомендован в аспирантуру, я обратился к заведующему кафедрой С.В.Валландеру с просьбой быть моим руководителем. А темой работы стали математические проблемы трансзвуковой газодинамики в плоскости годографа, которые я находил и формулировал сам. Сергей Васильевич мудро опекал моё саморазвитие, подпитывая вдохновение, обсуждая идеи и радуясь результатам. В 1957 году в Докладах Академии наук были напечатаны три моих работы, представленные академиком В.И.Смирновым. Математическую часть кандидатского минимума я сдавал комиссии в составе С.В.Валландера, В.И.Смирнова и Д.К.Фаддеева и, получив вопросы, рискнул отвечать сразу, без подготовки. Диссертация «Точное решение краевых задач для уравнения типа Чаплыгина» была защищена в срок, и меня оставили работать в должности ассистента на кафедре гидроаэромеханики математико-механического факультета Ленинградского государственного университета.

В обязанности ассистента входят обычно лабораторные, практические и семинарские занятия со студентами. Лабораторные работы я провёл по полному циклу, а прочих вспомогательных на кафедре было мало, так что сразу же пришлось читать лекции. Сначала спецкурс «Трансзвуковая газодинамика», потом, уже доцентом и профессором, общие курсы гидромеханики, газодинамики, аэродинамики разреженных газов, а также спецкурсы: гиперзвуковая аэродинамика, асимптотические методы, взаимодействие газов с поверхностями, - которые ставил сам. По этим же предметам вёл и спецсеминары. Немалую долю в учебном плане занимали курсовые и дипломные работы, темы которых я давал обычно с риском неудачи, так что нередко приходилось подключаться и выручать студентов. Работа с аспирантами тоже часто требовала активного участия в поисках эффективного решения поставленных задач. Поэтому некоторые публикации оказывались совместными. Я хорошо помню каждого из моих 34 кандидатов наук. Трое из них уже ушли из жизни. Пять учеников стали докторами. А вот дипломников запомнил не всех: их было около сотни.

С.В.Валландер скоропостижно скончался 19 июня 1975 года. Некоторое время я исполнял обязанности заведующего кафедрой. Однако, не обладая в должной мере искусством возможного, необходимым политикам любого масштаба, я подал в отставку, которая, хотя и не сразу, была принята в конце 1977 года. Кафедрой гидроаэромеханики в дальнейшем заведовали Н.Н. Поляхов, В.Г.Дулов, С.К.Матвеев. В 1983 году я был отстранён от преподавания в связи с участием в работе методологического семинара по семиодинамике, признанного партийными органами идеологически вредным. При очередном переизбрании в 1987 году меня перевели на должность профессора по §52 с последующим использованием преимущественно для научно-исследовательской работы.

С 1 сентября 1989 года я  прикомандировался в ДВГУ, г. Владивосток, где проработал два года в должности профессора кафедры математической физики, читая лекции по асимптотическим методам и краевым задачам гидроаэродинамики и руководя студенческими работами. После возвращения стал читать курс физики для математиков, а в последние годы основную часть учебного плана составил курс «Концепции современного естествознания» для гуманитарных факультетов университета. Образовательное пространство имеет три измерения: информационное, воспитательное и развивающее. Поэтому моим кредо в преподавательской деятельности всегда было стремление совмещать передачу знаний, воспитание стиля и развитие умения в целостном триединстве обучения.

Приоритет науки определил для меня стиль всей жизни. Полки с книгами вырастали в стеллажи, заполнявшими жилище. Рядом с рабочим столом появилась картотека книг и журнальных статей. Определился список изданий, регулярно просматриваемых на выставках новых поступлений в библиотеках университета и академии наук. Выписки, конспекты, переводы заполняли канцелярские тетради по разным разделам науки. Широкий фронт интересов постепенно фокусировался в тех направлениях, по которым шла работа на кафедре, читались лекции, выполнялись госбюджетные и хоздоговорные темы. Студенты, аспиранты, сотрудники привыкли каждую неделю ждать от меня свежую информацию по своим темам и живо обсуждать назревшие проблемы.

Трансзвуковая газодинамика вывела на краевые задачи математической физики с вырождением или сингулярностью на границах. Им был посвящён мой первый значительный цикл публикаций. Следующий составили работы по аэродинамике разреженных газов. Затем Сергей Васильевич предложил мне заняться проблемой взаимодействия разреженных газов с поверхностями космических аппаратов. Пришлось изучать физику поверхностей, теорию рассеяния, теорию случайных функций, ставить и решать задачи, различая молекулярный, кинетический и газодинамический уровни описания. Результаты этой работы составили предмет докторской диссертации и очередной монографии. Прикладные исследования велись по хоздоговорам с рядом серьёзных организаций, так что довелось встречаться и с Сергеем Павловичем Королёвым, которого в открытой печати тогда называли не иначе как  Главным Конструктором космонавтики. За эти работы в 1973 году С.В.Валландеру, мне и ещё нескольким сотрудникам из смежных организаций была присуждена Государственная премия.

Неожиданный кризис произошёл в 1983 году, когда партийные органы признали идеологически вредной работу методологического семинара по семиодинамике и меня отстранили от научного руководства тремя хоздоговорными работами по важнейшим темам. Распалась и группа моих сотрудников. Увлечение методологией было не случайным. Ещё в 1967 году я увидел, что в пространстве науки моя деятельность лучше проектируется не на плоскость задач, а на плоскость методов, где отчётливо определяются три группы: методы точные, асимптотические и эвристические. Осознание самоценности методов привело к инверсии приоритетов: не метод для задачи, а задача для метода. Тогда же был определён общий характер интересов: не численные процедуры, не теоремы существования и единственности, а вопросы аналитической формы и структуры. Предметное и методическое измерения научного пространства нуждались в дополнении семантической компонентой, выход на которую через динамику знаковых систем и был осуждён как идеологическая диверсия. Но эти же идеи вскоре пробились к жизни через синергетику, судьба которой оказалась более удачливой. Мои работы по тринитарной структуре целостности, выходя за рамки традиционной научной парадигмы, ищут сейчас осмысления в более широком, философском контексте.

За 50 лет научной работы количество карточек в моей библиографии выросло до 40 тысяч, число корреспондентов перевалило за 500, список публикаций насчитывает более 400 названий, включая 10 монографий и 5 учебных пособий. Кроме того, написано 14 отзывов на диссертации, 35 – на авторефераты, 18 - на книги, 75 – на статьи; 13 раз я был официальным оппонентом по докторским диссертациям, 42 – по кандидатским. В 70-е годы  трижды выдвигался в члены-корреспонденты Академии наук СССР, однако агитационной работы среди избирателей не вёл, а по гамбургскому счёту, стало быть, не потянул.

 

В начале 1956 года я познакомился со студенткой 5-го курса филологического факультета Юлей Поляковой. Начались свидания, провожания, объяснения, и в конце апреля 1956 года на квартире у Поляковых собрались наши друзья и родственники, чтобы погулять на свадьбе. Войти в добропорядочную семью после семи лет общежития оказалось непросто. Привычный распорядок дня был разным. Возвращаясь из библиотеки в 23 часа, я встречал укоризненный взгляд тёщи, которая считала себя вынужденной снова готовить ужин. Окончив университет, Юля стала работать в школе-интернате, а я всё ещё был аспирантом с непонятным будущим. Когда у нас 15 февраля 1957 г. родилась дочь Аня, отношения в семье проще не стали. Я обратился к Сергею Васильевичу с просьбой помочь мне получить своё жильё, несмотря на то, что прописка в общежитии была временной. И С.В.Валландер вместе с ректором А.Д.Александровым ходили в обком хлопотать за молодого ученика, подающего большие надежды. Нам дали две небольшие смежные комнаты в коммунальной квартире на Дровяном переулке. Квартира была на последнем этаже, крыша протекала и стены покрывались плесенью. Печь находилась у входной двери и тепло от неё до стен не доходило. Здесь 19 октября 1958 г. родился сын Алексей, и через некоторое время Юля была вынуждена пойти работать в детсад, чтобы устроить туда детей. В молодости сил хватает на все житейские проблемы. Мы справлялись и с печным отоплением, и с протечками, и даже с грозной соседкой, от которой бежали прежние жители. Однако здоровье детей нуждалось в подкреплении, и Летом Юля возила детей  на юг: в Скадовск, Евпаторию, Архипо-Осиповку. Бывая там с ними, я продолжал работать, пока они купались и загорали на море. В начале 60-х развернулось строительство жилья через кооперативы, и мы включились в университетский ЖСК. Трёхкомнатная «распашонка» на Тихорецком проспекте 10-1-56 площадью в 40 кв.м. стала нашей первой отдельной квартирой. Тут дети завершали детсад и начинали школу. Путь из детсада в школу здесь проделала и Юля. А я в 1964 г. защитил докторскую диссертацию. В те годы меня справедливо обзывали рационалистом. Строгий распорядок каждого дня недели с 8 до 23 часов заполняли лекции, семинары, библиотеки, сотрудники, аспиранты, студенты, книги, статьи,…, и Юля с трудом находила в этом плотном расписании щелочку, чтобы вписать туда слово «жена». Конечно, иногда мы ходили в гости, в кино, в театр, но это случалось не часто. Но как-то, оставив детей на Великой у бабушки, мы с Юлей вдвоём прошли путь от озера Рица до Красной Поляны. В другой раз по предгорьям Кавказа мы ходили вместе с малыми детьми в компании с друзьями. А на байдарке плавали вчетвером по реке Великой и на Байкале. Когда дети подросли, я брал их и в более серьёзные походы, но уже без мамы. Они побывали на Алтае, Кавказе, Памире. После школы Аня поступила на химический факультет ЛГУ, а Алёша – на мат-мех, астрономическое отделение. Всё шло нормально, хотя не всё из намеченного удавалось осуществить. Например, сорвалась совместная поездка в Танзанию по линии Юнеско. А в Польшу к друзьям семью отпустили без меня, хотя одного меня на зарубежные конференции выпускали. Правда, тоже не всегда. Много раз выездное дело бесследно терялось в бюрократических лабиринтах. Но всё же удалось побывать в Венгрии, Польше, Англии. В университете работа шла успешно. Отношения с Поляковыми тоже наладились. Юля мастерски преподавала литературу в школе. Дети хорошо учились. Жизнь вошла в спокойное русло.

Но…Разгром методологического семинара, начавшийся в 1983 году, лишил меня ряда прав и льгот, в частности на ЖСК. Вступаться за непонятную семиодинамику математики не стали. Оставались только самые верные друзья, и они действительно меня поддержали. Через год я уехал во Владивосток, где у меня появилась отдельная комната в общежитии, нормальная работа в университете и благоприятная обстановка в коллективе. Там я познакомился с новыми замечательными людьми, побывал в Уссурийской тайге, в пещерах Чиндолаза, в горах Сихотэ-Алиня, съездил на Сахалин и Курильские острова, открылся Океану. И хотя не смог или не успел завоевать его доверие в той же мере, в какой меня приняли Лес и Горы, чувство масштабности, необходимое для понимания крупных событий, во мне утвердилось. В июне 1991 г. я смог вернуться и поселиться в однокомнатной квартире, которую мне помог приобрести талантливый ученик Володя Энгельгарт, перешедший из науки в строительный бизнес. Время скитаний закончилось. Испытание, ниспосланное мне, возможно, было наказанием за жёсткий рационализм. Оно же открыло путь к целостности.

«Туристы – это бездельники, которые шляются, где попало, вместо того, чтобы работать», - так я думал почти до 30 лет. Перестройка сознания произошла в 1960 году, когда меня взяли в серьёзный поход на Алтай. С тех пор турпоходы стали нормой активной жизни. К 75 годам набралось 27 летних и 23 зимних похода. Туристские походы – прекрасный отдых для людей, поглощённых научной работой. Дело не только в красотах природы, ритме движения, смене впечатлений. Суровые условия решительно отвлекают от научных размышлений. Там, особенно зимой, приходится заботиться прежде всего о том, как обеспечить выживание. К вечеру каждого дня надо рыть в снегу яму или делать настил для костра, готовить лапник, ставить палатку, подвешивать печку и трубы, искать и валить сушины, пилить их и колоть дрова на костёр и печку. Всё это, несмотря на усталость, и побыстрее, пока не совсем стемнело. Если не сделаешь, к утру замёрзнешь. В трудных походных условиях проверяется крепость характера и прочность дружбы, той мужской дружбы, которая связывает меня с туристскими друзьями. Экстремальные условия, закаляя человека, могут раскрывать в нём такие способности, о которых он не подозревает и которые не поддаются научному объяснению. Дважды в походах во мне просыпался дар провидца. Из наших походных описаний можно составить целую книгу.

Эпистолярный жанр совершенно уникален. Сочетая в себе документальность рацио, задушевность эмоцио и зоркость интуицио, он не сводится ни к научным трактатам, ни к интимным дневникам, ни к эзотерическим таинствам. В нём всегда находил прибежище тот личностный эликсир, который не допускался в серьёзной литературе, претендующей на публикацию. Я насчитал более 500 человек, с которыми вёл переписку. Почти как у А.А. Любищева. Правда, не оставляя ни одного письма без ответа, я, в отличие от Любищева, писал коротко, сжато, излагая не свободный полёт мысли, а лишь выжимки размышлений. Самая мощная волна существенного общения пришла ко мне от А.А.Любищева. Другой сильный толчок дала драматическая история семиодинамики. Третья волна идёт от синергетики. Время меняет акценты ценности. Ветхие листочки могут стать важными документами истории. Просматривая послания из разных стран и из всех уголков России, я пытаюсь понять, чьи письма надо хранить особенно бережно. Пока в шкатулке раритетов вижу автографы, прежде всего, талантливых тружеников России: Николая Александровича Козырева, Льва Герасимовича Лойцянского, Юрия Михайловича Лотмана, Александра Александровича Любищева, Сергея Викторовича Мейена, Феликса Исидоровича Франкля, Юлия Анатольевича Шрейдера, Георгия Петровича Щедровицкого.

После долгих и трудных размышлений я решил опубликовать значительную часть своего эпистолярного архива. Цикл «Люди в письмах» состоит из семи томов: 1. Деловые и дружеские. 2. Вокруг А.А.Любищева. 3. Граждане науки. 4. Философия и синергетика. 5. Антропосфера. 6. Фрактальный социум. 7. Целостность и стиль. Восстановление переписки возвращает автора к прежним временам и проблемам, заставляя вновь переживать волнения тех дней, вспоминая забытые детали, переоценивая свои поступки, отмечая досадные промахи и радуясь удачным находкам (своим и встречным). Фехтовальность диалогического текста поддерживает напряжение интриги, возбуждает интерес и делает эпистолярный жанр притягательным для читателя. Чтение писем известных тебе людей интригует открытием тонких сторон их души, вселяет радость и удивление богатством человеческой натуры. Но каждый раз возникает опасение, не снизится ли их облик под бременем суеты бытовых деталей. Ведь, как признавал Александр Сергеевич,  «пока не требует поэта к священной жертве Аполлон, в заботах суетного света он малодушно погружён». Поэтому публикатор постоянно ощущает себя в напряжении этического контроля. Однако обитатели Олимпа, ответственные (возможно по совместительству) за эпистолярную сферу, оказываются достаточно требовательными, чтобы достойные люди сохраняли свой уровень в письмах через магию стиля. Честный стиль – чуткий и надёжный навигатор. Безопасно, безобидно, безвредно ведёт он эпистолярный диалог сквозь рифы низких истин и мифы ложных домыслов, и дарит читателю реалии современной жизни, характеры незаурядных личностей,  размышления о высших ценностях,  не допуская при этом ни секретных сведений, ни интимных признаний, ни опасных заявлений. Содержание писем, интрига, значимость - неоднородны. Одних читателей заинтересует предмет переписки, других привлекут характеры людей – авторов писем, третьи найдут свежие краски в срезе социальной истории, отражённой в этих письмах. В любом случае читатель видится разнообразным, а чтение – избирательным. «Нам не дано предугадать…».

Кроме эпистолярного цикла, за последние годы изданы «Становление тринитарного мышления»-2005, «История семиодинамики»-2006, «Крупицы памяти»-2007. Задуманы «Знаки внимания» и «Вешки интереса», на которые есть ещё почти пять лет.

У меня сейчас относительно спокойная полоса жизни. Сил пока хватает, чтобы трудиться на полную ставку. Хочется думать, что вечер ещё не поздний и кое-что существенное ожидает меня впереди. Надо бы вспомнить о поездках, конференциях, лекциях в разных городах, встречах с интересными людьми. Заглянуть в сложную переписку с ближайшими родственниками. И оформить, наконец, завещание. Правда, не очень понятно, о чём в нём писать. Ведь всё уже роздано. Драматическая ситуация, когда к уходящему предку съезжаются наследники в ожидании своей доли, мне не угрожает.

В чём смысл бытия? Вряд ли найдётся человек, который никогда не задавал этого вопроса, себе или другим, хотя бы мысленно. И вероятно правы те, кто полагает, что понимание смысла чего-либо невозможно изнутри; требуется увидеть это извне, выйдя туда хотя бы частично. Значит ли это, что пока мы живы, смысл жизни для нас сокрыт? И кто хочет быстрее дойти до смысла, должен поторопиться умереть? Однако люди – не только живые существа, но и существа мыслящие. Кроме биосферы, им доступна ноосфера. Судить о жизни человек может извне, не умерев, а поднявшись в пространство разума и духа, в ноосферу. Там, надо полагать, будет шанс обнаружить искомый смысл. Не умея пока достаточно уверенно ориентироваться в ноосфере, я удовлетворяюсь ответом: «Смысл жизни – в осуществлении». Правда, такой ответ сразу же требует уточнения: «В осуществлении чего?». Ожидаемое «Себя» вряд ли нас устроит. Лучше сказать: «Того, что заложено в тебе природой». В понимание природы я включаю здесь и сознательную компоненту, которую называют по-разному: Бог, Демиург, Создатель, Творец, Вселенский Разум, Самоорганизующаяся Вселенная и т.п. Как же определить своё предназначение, допуская направляющую роль провидения вместе со свободой нашей воли?

Говорят, кому много дано, с того много и спрашивается. Это кажется справедливым. Но интереснее обратная теорема: Много спрашивается – значит много дано. Действительно, загружают того, кто везёт, а с пустого и беспомощного – какой спрос?! Отвечая на вызовы судьбы, мы активизируем свой потенциал, раскрывая его глубины и тайны, осознавая тем самым своё призвание. Мне довелось пережить несколько критических моментов, которые синергетики называют точками бифуркации. В них прежняя траектория теряет устойчивость, а попадание на одну из новых зависит от внутренней асимптотики, не зная которой, говорят о хаосе случайных влияний. Оглядываясь сейчас на эти узловые события, я вижу три фактора, взаимодействие которых определяло выбор дальнейшего пути. Во-первых, генетическая основа, под которой я подразумеваю не только родительские гены, но и всё ментальное наследие Малой Родины. Во-вторых, индивидуальная склонность к непонятному, неизвестному, неосвоенному, любопытство на грани авантюризма. В-третьих, заботливая рука судьбы, ангел-хранитель, благо провидения. Были моменты, когда эта невидимая рука отводила меня от слишком благополучного пути или же спасала от гибели в чрезвычайной ситуации.

Что касается ментального наследия, то на вятской земле не было помещиков и крепостных, а были вольные поселенцы, осваивающие новые территории. Названия деревень типа «Мишина расчистка» и «Николин починок» говорят сами за себя. Поэтому в нашем менталитете нет синдромов господства и рабства, а есть хозяйская ответственность за принятое дело. Ответственность за всех, кого “приручил”, о которой писал Сент-Экзюпери, у вятского труженика распространяется и на животных, которых он содержит, и на дом, в котором живёт, и на землю, которую обрабатывает. Склонность к неизведанному доставила мне немало проблем в жизни, а в работе она проявилась в том, что, освоив какую-то область, я не задерживался в ней надолго, не закреплялся, не выращивал научной школы. Вряд ли это положительное качество. Но освоенное и понятое переставало увлекать, интерес устремлялся к новым проблемам. Кстати, в турпоходах мы тоже предпочитали маршруты по бездорожью. Руку судьбы признают далеко не все. Я тоже, пока не ощущал её, будучи рационалистом, полагал, что делаю себя в социуме сам. Но мир устроен значительно сложнее, чем наше представление о нём. Судьбоносные события видимо всё-таки существуют. Реализовал ли я свой потенциал? Осуществился ли? Программа, конечно, не исчерпана, да и к незапланированному я открыт. Но главное, пожалуй, свершилось. Когда-то в зимнем походе по Хибинам после преодоления основного перевала я сказал ребятам: «Поход ещё не закончен, но уже состоялся». Так можно сказать и о жизни, которая осуществлялась в эти прошедшие годы.                      Р.Г. Баранцев                                                          2008.

 

 

 

 

 

 

 

 

3.   Scientific, Pedagogic and Social Activities of Professor, Doctor of Technical Sciences

Basin Mikhail Abramovich – A Short Summary.

 

 

Basin Mikhail Abramovich was born June 11, 1939 in City of Leningrad. After graduating a middle school with a Gold Medal in 1956, he started studying at the Leningrad Shipbuilding Institute, which he graduated with honors in 1962. From 1960 to 1992 he has worked in the Central Scientific Research Institute named after Academician A. N. Krylov (CSRI), starting as a technician. After graduating the Leningrad Shipbuilding Institute he consecutively took up the positions of junior, senior, and lead research member of technical staff.

In 1963 M. A. Basin entered the post-graduate program at CSRI. He graduated on February 24, 1967 successfully defending the candidate dissertation titled “Theoretical and Experimental Investigation of Hydrodynamic Characteristics of Cavitating and Ventilated Hydrofoils” (Diploma dated June 28, 1967, protocol N27/2228).

On December 8, 1976 Mr. Basin was promoted to the position of a senior scientific member of technical staff (Diploma CH-N 004394, protocol N 48/5) in Ship Theory.

On July 1, 1984 he successfully defended a doctor dissertation in the field of Ship Theory “Theoretical - experimental Investigation of Hydro-aerodynamics of Fast Ships.”

On February 10, 1985 Mr. Basin was approved in the rank of doctor of technical sciences (Diploma TH N 004166, Protocol N 5d/6).

During his career in CSRI he published more than 80 research works in the areas of optimal design of the hull forms of fast ships, developing new methods of solution of equations of hydrodynamics and dynamics of ship, theory of a foil in proximity to the free surface, cavitation, ventilation, theory of waves and vortices. Among them two monographs are worth mentioning, “Artificial Cavitation”, 1971 (co-authored with I. T. Egorov, I. I. Isaev, Ju. M. Sadovnikov), and “Hydro-aerodynamics of the Foil near the Free Surface”, 1980 (co-authored with V. P. Shadrin).

Doctor M. A. Basin has carried out and managed many projects related to hydro-aerodynamics and design of fast ships of different types. He has participated in design and analysis of hydrodynamic configurations of most Soviet hydrofoil crafts and multiple fast ships. These works required not only rigorous theoretical and experimental investigations, but development of experimental facilities capable of modeling cavitation of lifting hydrofoil systems and control surfaces and lift augmentation means for high speed ships. Such equipment was developed under leadership of Dr. M. A. Basin.

On the course of his work he has been granted nine patents (invention certificates), that reflected his achievements in design and construction of fast ships. All of them were equipped with hydrofoil systems whose profiles were proposed by Mr. M. A. Basin. One of his inventions, in which he was proposed an original novel method of minimizing of rocking motion of gliding ships, had received the Golden Medal on the international exhibition of inventions and discoveries “Eureka” in Brussels.

Under his leadership and with his active participation, a principally new phenomenon of resonance interaction in the continuous medium between a flow near the lifting bodies and waves has been discovered. Results of this research were published in many papers and monographs; they laid the base for a series of inventions.

In 1986 Dr. M. A. Basin was invited to Leningrad Shipbuilding Institute (Saint Petersburg State Marine Technical University) to teach in the department of Applied Mathematics and Mathematical Modeling; on June 27 of 1990 he was elected to take a position of professor in the same department. At the same time he taught courses in the Institute of Professional Advancement in Shipbuilding Industry and in the Baltic Institute of Psychology, Politics and Justice. He prepared the following courses of lectures,

1.   Hydro-aerodynamics of Fast Ships;

2.   Development of Mathematical Models in Ship Theory;

3.   Computational Methods of  Mathematical Physics in Marine Technology;

4.   Synergetics;

5.   Theoretical Foundations and Practical Applications of Synergetic Methodology in Investigation and Prognosis of Complex Self- organizing Systems;

6.   Resonances in Nature and Technology. Vortex-Wave and (or) Structural Resonance;

7.   Synergetics and Mankind.

Working as Professor, M. A. Basin published a series of scientific works and presented a series of papers on All-Russia and international conferences. In co-authorship with I. T. Egorov and N. Ju. Zavadovsky he published methodological textbook “Application of Computers in Ship Hydrodynamics”. He co-authored with N. V. Kornev and A.V. Kudrjavtzev he wrote the methodological computer textbook “Vortices”, which has been used in teaching process in Saint-Petersburg State Marine Technical University.

On April 2, 1992 Dr. Basin received a professorship certificate for the Department of Applied Mathematics and Mathematical Modeling of Saint-Petersburg State Naval Technical University (diploma N 000052).

Since 1969, M. A. Basin has been an organizer and a head of the monthly seminar “High Speed Hydrodynamics”; selected materials from this multi-year work where published in three collections of papers by the Science and Technology Society for Shipbuilding Industry under his scientific edition. In the course of the seminar, Mr. Basin, in cooperation with the Seakeeping Section of the Society, has organized three Scientific Conferences on investigation of vortex and wave flows in the hydrodynamics of fast ships. Many of participants of the seminar established themselves as outstanding scientists, doctors and candidates of sciences.

Professor M. A. Basin originated a scientific school in the area of new methods of solution of equations in ship hydrodynamics and dynamics. He has repeatedly participated as an official opponent in the public defense of candidate and doctor dissertations in the Saint-Petersburg universities, as well as outside the city.

From 1992 to 1998 he worked as a scientific deputy director in Research and Development private firm “Forma”, were he continued to study design and analysis of hydrodynamic complex of fast ships. His interests were focused on design of fast ships with hybrid hydrodynamic support, and on development of perspective fast ships. During the course of this work he published 6 papers in the international conferences.

From 1994 to 1999 M. A. Basin has worked as a professor in the Department of Ship Theory in Navy Engineering School (City of Pushkin). Working in this department, he has prepared and taught lectures “Ship Dynamics” and took active part in founding and development of new areas of scientific research, in particular, investigation of influence of stratification on the forces, acting on the seagoing objects; self-stabilization of seagoing vehicles in waves. During his work in the department he obtained new theoretical result about anomalous resonance behavior of lifting bodies in stratified liquid, which appeared as one of modifications of the phenomenon of vortex-wave and (or) structural resonance unveiled earlier by him. Professor M. A. Basin has provided substantial help in preparation and defense of doctor dissertations by the department members of technical staff.

 

M. A. Basin has been a recipient of the following diplomas from the Science and Technology Society for Shipbuilding Industry.

May 18, 1971. Academician A.N. Krylov diploma for the best work in the area of the ship theory and hydrodynamics under the title, “Investigation of Hydrodynamic Characteristics of Hydrofoils Moving Near the Free Surface”.

May 8, 1973. Academician A. N. Krylov diploma for the best work on the ship theory and hydrodynamics “Artificial Cavitation”.

November 20, 1980. Diploma for the best experimental work in hydrodynamics of ships, “Experimental Setup and Equipment for Testing of Hydrofoils in a Cavitation Tank”.

October 13, 1981. Academician A.N. Krylov diploma for the best work on the ship theory and hydrodynamics, “Hydro-aerodynamics of a Wing Near the Free Surface’, a monograph.

From 1962 to present, professor Basin has participated in more than 100 scientific and technology conferences, among them more than 30 international conferences in Australia, Austria, Belgium, Bulgaria, Croatia, Great Britain, Germany, Greece, Italy, Japan, Russia, USA, Ukraine.

Professor M. A. Basin has lead work a variety of scientific societies. In 1980 he was elected as a member of the Central Executive Committee of the seakeeping section of Science and Technology Society for Shipbuilding Industry. In 1994 and 1995 he helped to organize two international conferences. One of them was dedicated to the memory of his father, professor Abram Moiseevich Basin, an outstanding Soviet scientist. The works of this Conference, edited and published by M. A. Basin, are now in libraries around the world.

At 1993 M.A. Basin became a member of the Saint-Petersburg Association of Scientists and Scholars (SPASS), and from 1994 to 2000 he has served as a member of its Coordinate Committee. Currently he is the member of Scientific Board of SPASS. In May 1993 he organized the round table “Synergetics and Methods of Science” with participation of Saint – Petersburg leading scientists; in September 1993 he organized an interdisciplinary scientific seminar “Synergetics and Methods of Science” affiliated with the Saint -Petersburg Scientific Center under RAS and SPASS. During 18 years, the seminar attracted more than 50 scientists from Saint –Petersburg and other Russian cities, as well as foreign participants. Within the seminar two Round tables “Synergetics and Language” and “Synergetics and Psychology” were arranged, with Russian and foreign presenters. The transactions of the round tables, “Synergetics and Psychology” were published in 1997. Papers were edited by M. A. Basin and S. V. Haritonov.

In September 1995 the Saint-Petersburg Association of Scientists and Scholars organized the Research Center “Synergetics” under leadership of  M. A. Basin. Since then the center does scientific-research and educational work, provides networking with scientists from Russia, Ukraine, Belorussia and other countries. It could be said the Saint-Petersburg scientific synergetic school has been established.

M. A. Basin and other members of the Center have taken part in the series of international conferences: International Moscow Synergetic Forum, organized by Institute of Philosophy of Russian Academy of Sciences (Moscow, 1996), and conference: “Problems of Noosphere and Sustainable Development” (1996), in the First Russian Philosophical Congress (1997), organized by Saint-Petersburg State University in Saint-Petersburg and so on.

Since 1995, projects of the Center “Synergetics” have been financed by the Russian Foundation for Fundamental Research.

Grant of RFFI N 95-01-01582a – “Synergetics. Methods of Investigation of Complex Self-organizing Systems”, 1995; Principal investigator was M.A. Basin.

Crant of RFFI N 96-06-80418a - “Investigation of Structural Laws of Self-organization in Open Systems”, 1996 – 1997; Principal investigator was M.A. BАsin.

Grant of RFFI N97-06-87108d - ”Publication of Collection of Works of Seminar “Synergetics and Methods of Science”, 1997-1998; Principal investigator was M.A. Basin.

Grant of RFFI N 00-06-80077a - “Synergetics. Investigation of Structural Laws of Development of Mankind Society as Self-organizing Open System”, 2000-2001; Principal investigator was M.A. Basin.

 

In 1998 the Saint-Petersburg publishing house “Nauka” issued, under the grant of RFFI, the transactions of the seminar “Synergetics and Methods of Science”, edited by M. A. Basin.

By present time, the results of the scientific activity of M. A. Basin in the area of Synergetics have been summarized and published in several papers in the International conferences in Moscow, Saint-Petersburg, Tver’, Novorossiysk, Cheboksary, Novosibirsk, Alushta, Heraclion (Greece), Brussels (Belgium), Rostock (Germany).

The following monographs were published during the period from 1999 to 2008,

M. A. Basin, I. I. Shilovich: “Synergetics and Internet (Path to Synergonet)”, SPb., “Nauka”, 1999, 72 pp.

M. A. Basin “Waves. Quanta. Occasions. Wave Theory of Interaction of Structures and Systems. Part 1”, SPb., “Norma”, 2000, 168 pp.

M.A. Basin “Computers. Vortices. Resonances. Wave Theory of Interaction of Structures and Systems. Part 2”. SPb: “Norma” 2002. 144 pp.

In 2004, the second tome from the series of monographs by Basin M. A., Shilovich I. I., devoted to investigation of Internet: “Path in Synergonet” was published by “Norma” (128 pp).

In 2003-2008 the following monographs by M. A. Basin in cooperation with G. I. Basina were published,

1.   Basina G. I., Basin M. A. ”Synergetics. Evolution and Rhythms of Mankind”. SPb.: “Norma”. 2003. 260 pp.

2.   Basina G. I., Basin M. A. “Synergetics. The Principles of Methodology”. SPb.: “Norma”. 2006. 56 pp.

3.   Basina G. I., Basin M.A. “Synergetics. Universe of Resonances”. SPb.: “Norma” 2008. 144 pp.

 

At the same time M. A. Basin took active part in three projects of RHSF, which were completed in cooperation with Byelorussian scientists (principal contributor from Russian side was doctor of physical-mathematical sciences, professor R. G. Barantsev).

1. “Fullness and Wholeness as Imperatives of Contemporary Scientific and Humanitarian Knowledge”. (Grant 00-03-3600a/B).

2. “Synergetic Interpretation of Information Universe.” (Grant 03-03-00247a/B).

3. “Innovative Potential of Synergetic Methods in Diagnostic, Synthesis and Design of Complex Systems”. (Grant 07-03-90309a/B).

At present time M. A. Basin with the co-author G. I. Basina online published ten papers and essays dedicated to different aspects of the  synergetic methodology. It was done in memory of centennial of outstanding scientist professor Abram M. Basin. United under one concept, essays formed the first part of new electronic monograph titled ”From Numbers of Basin to Synergonet”.

The main scientific achievements of Dr. M. A. Basin in the area of Synergetics are:

1.   Development of principles of Synergetics methodology.

2.   Introduction of conception of  parameter of wholeness, which integrally describes dynamics of a complex system.

3.   Development of an algorithm describing dynamics of system with finite number of states. Suggestions about computer realization of this algorithm.

4.   Idea of Holistic computer.

5.   Development of information-wave theory of structures and systems.

6.   Classification of nonlinear waves, vortex, mushroom and tree structures and transport - information systems.

7.   Discovery of the phenomenon of vortex-wave resonance in motion of the bodies in the continuous medium.

8.   Development of the concept of vortex-wave and (or) structural resonance. Suggestions for the application of this conception.

9.   Introduction to and consideration of triad, describing a transport-information system. Determination of conception of a controller.

10.                       Classification of transport-information systems.

11.                       Application of synergetic methodology to the investigation of the Internet.

12.                       Introduction of the concept of Synergonet as an attractor in dynamics of mankind society.

13.                       Working out of complex mathematical models of  living systems and mankind society.

14.                       Suggestion about using of complex differential equations for describing of development of catastrophic events.

15.                       Development of the concept of inner time of the system and external time of the field and its mathematical realization.

16.                       Working out the principles of complex power geometry.

17.                       Investigation of geometry and bifurcation dynamics of exponent of circumference. Analysis of Basin’s bifurcation numbers.

 

Results of professor M. A. Basin research were summarized in ten monographs and collections of papers, two methodological textbooks, and also in more than 230 scientific papers.

 

 

 

 

 

 

 

 

4. Краткая характеристика научной, педагогической и общественной деятельности профессора, доктора технических наук

Басина, Михаила Абрамовича.

 

Басин, Михаил Абрамович, родился 11 июня 1939 года в г. Ленинграде. После окончания с золотой медалью в 1956 году средней школы он в том же году поступил в Ленинградский кораблестроительный институт, который окончил с отличием в 1962 году. С 1960 по 1992 год он работал в ЦНИИ им. акад. А.Н. Крылова сначала на должности техника, а после окончания Ленинградского кораблестроительного института последовательно занимал должности младшего, старшего и ведущего научного сотрудника.

В 1963 году М. А. Басин поступил в аспирантуру ЦНИИ имени акад. А.Н. Крылова, по окончании которой 24 февраля 1967 года защитил кандидатскую диссертацию на тему: “Теоретическое и экспериментальное исследование гидродинамических характеристик кавитирующих и вентилируемых подводных крыльев” (диплом MTH-N 029101 от 28 июня 1967 года, протокол N27/2228).

8 декабря 1976 года ему было присвоено звание старшего научного сотрудника (диплом CH-N 004394, протокол N 48/5) по теории корабля.

1 июля 1984 года он защитил докторскую диссертацию по специальности: теория корабля на тему: “Теоретико-экспериментальное исследование гидроаэродинамического комплекса быстроходных судов”

10 февраля 1985 года ему присваивают степень доктора технических наук (диплом TH N 004166, протокол №5d/6).

За время работы в ЦНИИ им акад. А. Н. Крылова им было опубликовано более 80 научных работ в области оптимального проектирования обводов быстроходных судов, разработки новых методов решения уравнений гидродинамики и динамики судна, теории крыла, движущегося вблизи границы раздела сред, кавитации, вентиляции, теории волн и вихрей. Среди них - две монографии: “Искусственная кавитация”-1971 год (совместно с И. Т. Егоровым, И. И. Исаевым, Ю. М. Садовниковым), ”Гидро - аэродинамика крыла вблизи границы раздела сред”-1980 год (совместно с В. П. Шадриным).

М. А. Басин был руководителем и участником нескольких десятков тематических и договорных работ по гидро - аэродинамике и проектированию быстроходных судов различных типов. Он принимал участие в отработке гидродинамического комплекса большинства советских судов на подводных крыльях и других типов быстроходных судов. Эти работы потребовали не только серьёзных теоретических и экспериментальных исследований, но и создания оборудования для обеспечения возможности моделирования кавитации несущих крыльевых систем и органов управления быстроходных надводных судов и кораблей в кавитационном бассейне. Такое оборудование было создано под руководством М. А. Басина.

На основании выполненных исследовательских работ им было получено девять авторских свидетельств, внедренных при проектировании и строительстве ряда быстроходных судов и кораблей. На многих из судов были установлены крыльевые системы с профилями, предложенными М. А. Басиным. Одно из его изобретений, в котором предлагался принципиально новый способ снижения параметров качки глиссирующих судов, получило в 1995 году золотую медаль на международной выставке изобретений и открытий “Эврика” в Брюсселе.

Под его руководством и при его активном участии было открыто принципиально новое явление резонансного взаимодействия потока около несущих тел с волнами, возникающими в неоднородной среде. Результаты сделанного открытия опубликованы в ряде статей и на их основе сделан ряд изобретений.

В 1986 году он был приглашен в Ленинградский кораблестроительный институт (Санкт-Петербургский государственный морской технический университет) на кафедру прикладной математики и математического моделирования и 27 июня 1990 г. был избран на должность профессора той же кафедры. Одновременно он читал лекции в Институте повышения квалификации работников судостроительной промышленности и в Балтийском институте психологии, политики и права. Он подготовил следующие курсы лекций.

1) Гидро - аэродинамика быстроходных судов.

2) Построение математических моделей в теории корабля.

3) Расчётные методы математической физики, связанные с судостроением.

4) Синергетика.

5) Теоретические основы и практические приложения синергетической методологии исследования и прогнозирования динамики сложных самоорганизующихся систем

6) Резонансы в природе и технике. Вихре – волновой и (или) структурный резонанс.

7) Синергетика и Человечество.

Работая профессором, он опубликовал ряд научных работ и представил ряд докладов на Всероссийские и Международные конференции. В соавторстве с И. Т. Егоровым и Н. Ю. Завадовским им было опубликовано методическое пособие (монография) “Применение вычислительных машин в расчетах гидродинамики судна”. В соавторстве с Н. В. Корневым и А.В. Кудрявцевым им было создано компьютерное методическое пособие “Whirlies”, которое использовано в учебном процессе Морского технического университета.

2 апреля 1992 М. А. Басину было присвоено звание профессора по кафедре прикладной математики и математического моделирования Санкт-Петербургского государственного морского технического университета (диплом N 000052).

В 1994 году он был приглашен в г. Загреб (Хорватия) для чтения лекций по гидро-аэродинамике быстроходных судов.

Начиная с 1969 года М. А. Басин руководил семинаром “Гидродинамика высоких скоростей”, материалы работ которого были выпущены в трех сборниках Трудов Научно-технического общества судостроительной промышленности под его научной редакцией. В рамках семинара им совместно с секцией мореходных качеств НТО СП были организованы Научно-технические конференции по исследованию вихревых и волновых движений жидкости при движении быстроходных судов. Большинство участников семинара М. А. Басина стали в настоящее время видными учеными, докторами и кандидатами наук.

Профессор Басин является создателем научной школы по разработке новых методов решения уравнений гидродинамики и динамики судна. Он неоднократно выступал в качестве оппонента при защите кандидатских и докторских диссертаций в Советах Санкт-Петербургских университетов и университетов других городов .

C 1992 по 1998 годы он работал заместителем директора по научной работе НПО “Форма”, где занимался исследованиями в области проектирования гидродинамического комплекса высокоскоростных судов. Его интересы при работе в НПО были обращены на проектирование судов с комбинированными принципами поддержания, а также на определение перспектив и путей дальнейшего развития быстроходных судов. По этой тематике им было опубликовано 6 докладов на международных конференциях.

С 1994 по 1999 год М.А. Басин работал профессором кафедры теории корабля Высшего военно-морского инженерного училища (г. Пушкин). За время работы на кафедре он подготовил и прочитал курс: “Динамика корабля”, а также принял активное участие в обосновании и разработке новых научных направлений, успешно развиваемых на кафедре: исследование влияния стратификации на силы, действующие на морские объекты, создание волностойких морских объектов. Во время работы на кафедре им был получен также важный новый теоретический результат об аномальном резонансном поведении несущих тел в стратифицированной жидкости, являющийся частным проявлением открытого им ранее вихре-волнового и (или) структурного резонанса. Профессор Басин М.А. оказывал существенную помощь в качественной подготовке и защите докторских и кандидатских диссертаций сотрудниками училища.

М. А. Басиным были получены следующие дипломы Научно-технического общества судостроительной промышленности.

18 мая 1971 года. Диплом за лучшую работу по теории корабля и гидродинамике имени акад. А. Н. Крылова под названием: ”Исследование гидродинамических характеристик подводных крыльев, движущихся вблизи границы раздела сред”.

8 мая 1973 года. Диплом за лучшую работу по теории корабля и гидродинамике имени акад. А.Н. Крылова под названием: ”Искусственная кавитация”.

20 ноября 1980 года. Диплом за лучшую работу по экспериментальной гидродинамике судна за комплекс работ: “Комплекс устройств и приборов для испытаний подводных крыльев в кавитационном бассейне”.

13 октября 1981года. Диплом за лучшую работу по теории корабля и гидродинамике за монографию: “Гидро-аэродинамика крыла вблизи границы раздела сред”.

Начиная с 1962 года профессор Басин М.А. участвовал в более 100 научно-технических конференциях, из них в более 30 международных (в Австралии, Австрии, Бельгии, Болгарии, Великобритании, Германии, Греции, Италии, России, США, Украине, Хорватии, Японии).

Проф. Басин М.А. ведёт большую научно-общественную работу. В 1980 году он был избран членом Центрального правления секции мореходных качеств НТО СП. В 1994 и 1995 при его активном участии были организованы две Международные конференции, одна из них была посвящена памяти его отца Басина Абрама Моисеевича - выдающегося советского ученого - кораблестроителя. Труды этой конференции, изданные под научной редакцией М. А. Басина, имеются в ведущих библиотеках мира.

В 1993 году М. А. Басин вступил в Санкт-Петербургский союз ученых (СПбСУ) и с 1994 по 2000 годы являлся членом его координационного комитета. В настоящее время он является членом Научного совета Союза учёных. В мае 1993 года им был проведен Круглый стол: “Синергетика и методы науки”, - в котором приняли участие крупные ученые Санкт-Петербурга, а с сентября 1993 года им был организован при Санкт-Петербургском научном центре РАН и СПбСУ междисциплинарный научный семинар “Синергетика и методы науки”. В течение 18 лет на семинаре с докладами выступило более пятидесяти крупных ученых Санкт-Петербурга и других городов России и зарубежных ученых. В рамках семинара было проведено два Круглых стола: “Синергетика и язык” и “Синергетика и психология”, в которых приняли участие ученые различных городов России, ближнего и дальнего зарубежья. Труды круглого стола “Синергетика и психология” были изданы в 1997 году виде сборника докладов под редакцией М. А. Басина и С. В. Харитонова.

В сентябре 1995 года при Санкт-Петербургском союзе ученых под руководством М. А. Басина был организован научно-исследовательский центр “Синергетика”. В настоящее время центр “Синергетика” ведет большую научно-исследовательскую и просветительную работу, имея широкие научные связи с учеными различных городов России, Украины, Белоруссии и дальнего зарубежья. Формируется Санкт-Петербургская синергетическая школа.

М. А. Басин и сотрудники центра участвовали в ряде международных конференций: Международном Московском Синергетическом Форуме, организованном Институтом Философии РАН (Москва, 1996); конференции “Проблемы Ноосферы и устойчивого развития” (1996), в Первом Российском философском конгрессе (1997), организованных СПбГУ (Санкт-Петербург) и других.

Проекты центра “Синергетика”, начиная с 1995 года, финансируются Российским фондом фундаментальных исследований:

1.   Грант РФФИ №95-01-01582а - “Синергетика. Разработка методов исследования сложных самоорганизующихся систем”. 1995 год. Руководитель М. А. Басин

2.   Грант РФФИ №96-06-80418а - “Исследование структурных закономерностей самоорганизации открытых систем”. 1996-1997 годы. Руководитель М. А. Басин.

3.   Грант РФФИ №97-06-87108д - Издание сборника трудов семинара “Синергетика и методы науки”. 1997-1998 годы. Руководитель М. А. Басин.

4.   Грант РФФИ № 00-06-80077а «Синергетика. Исследование структурных закономерностей развития человеческого общества как самоорганизующейся открытой системы». (руководитель М. А. Басин).

В 1998 году Санкт-Петербургское издательство «Наука» по гранту, полученному от РФФИ, .выпустило в свет под научной редакцией М.А. Басина сборник трудов семинара: «Синергетика и методы науки», в котором были опубликованы наиболее интересные доклады выдающихся учёных, сделанные на заседаниях семинара.

В настоящее время результаты научной деятельности М. А. Басина в области синергетики обобщены в нескольких десятках докладов на международных конференциях в Москве, Санкт-Петербурге, Твери, Новороссийске, Чебоксарах, Новосибирске, Алуште, на острове Крит (Греция), Брюсселе (Бельгия), Ростоке (Германия) и в вышедших в 1999 и 2008 годах монографиях:

М. А. Басина и И. И. Шиловича: «Синергетика и Internet (Путь к Synergonet)» СПб.: "Наука" 1999 .71с.;

М. А. Басина «Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Часть 1.» СПб.: Норма. 2000. 168с.;

М. А. Басина «Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть2». СПб.: Норма. 2002. 144 с.

В 2004 году вышла в свет вторая из серии монографий Басина М. А. и Шиловича И. И., посвящённых исследованию Internet, «Путь в Synergonet». СПб.: Норма. 128с.

В 2003 -2010 годах вышли из печати написанные М. А. Басиным совместно с Г. И. Басиной монографии:

1.   Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. СПб.: Норма. 2003. 260 с.

2.   Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб.: Норма. 2006. 56 с.

3.   Басина Г.И. , Басин М. А. Синергетика. Вселенная резонансов. СПб.: Норма. 2008. 144 с.

В это же время М. А. Басин активно участвовал в трёх проектах РГНФ, осуществлявшихся совместно с белорусскими учёными (руководитель с Российской стороны д.ф-м.н., проф. Р. Г. Баранцев).

1. Полнота и целостность как императивы современного естественнонаучного и гуманитарного знания (грант 00-03-3600а/Б),

2. Синергетическая репрезентация информационного универсума (грант 03-03-00247а/Б),

3. Инновационный потенциал методов синергетики в диагностике, синтезе и проектировании сложных систем (грант 07-03-90309а/Б).

В настоящее время М. А. Басин совместно с Г. И. Басиной опубликовал в Internet, в честь столетия со дня рождения выдающегося учёного-кораблестроителя, профессора Абрама Моисеевича Басина, 10 статей-этюдов, посвящённых различным аспектам синергетической методологии. Объединённые одной идеей, этюды формируют первую часть новой электронной монографии, названной «От чисел Басина до Synergonet».

Основными научными достижениями М. А. Басина в области Синергетики являются:

1.   Разработка основных положений синергетической методологии.

2.   Введение представления о параметре целого, интегрально описывающем динамику целостной системы.

3.   Разработка общего алгоритма описания динамики системы с конечным числом состояний. Предложения по компьютерной реализации разработанного алгоритма.

4.   Идея целостного компьютера.

5.   Развитие информационно-волновой теории структур и систем.

6.   Разработка новой классификации нелинейных волн, вихревых, грибовидных, древовидных структур, транспортно-информационных систем.

7.   Открытие явления вихре - волнового резонанса при движении тел в неоднородной среде.

8.   Разработка концепции вихре - волнового и (или) структурного резонанса. Предложения по использованию этой концепции.

9.   Введение в рассмотрение триады, описывающей транспортно-информационную систему. Определение понятия контроллера.

10.                       Классификация транспортно-информационных систем.

11.                       Применение синергетической методологии к исследованию Internet.

12.                       Введение представления о Synergonet, как аттракторе динамики человеческого общества.

13.                       Разработка комплексных математических моделей живых систем и человеческого общества.

14.                       Предложение об использовании комплексного дифференциального уравнения для описания развития катастрофических событий.

15.                       Развитие представления о внутреннем времени системы и внешнем времени

16.                       Разработка основ комплексной степенной геометрии.

17.                       Исследование геометрии и бифуркационной динамики экспоненты окружности. Введение в рассмотрение чисел А. М. Басина.

Результаты исследований профессора Басина М. А. нашли свое отражение в 10 монографиях и сборниках статей, двух методических пособиях, а также в более 230 опубликованных в печати и в Internet статьях и докладах.

 

 

 

                                                 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5.Краткая характеристика научной и общественной деятельности Басиной

                                                          Галины Ивановны.

 

Басина Галина Ивановна родилась в блокадном Ленинграде 25 марта 1943  года.

В 196    1 году она окончила среднюю школу и, получив конструкторское образование прорабтала два года в ЦНИИ  имени академика А. Н. Крылова

В  1965 году она поступила на экономический факультет Ленинградсого Института Водного Транспорта,, который закончила в 1969 году .

После окончания Института она осталась работать на кафедре экономики водного транспорта в должности младшего научного сотрудника.

Во время работы на кафедре  Г. И .Басина принимала участие в выполнении ряда  тематических и договорных научно-исслеолательских работ в области экономики речного флота.

В 1992 году Г И. Басина была приглашена на Научно-производствкнное предприятие  Форма на должность экономиста, где принимала активное участие в работах ло зкономическому обоснованиию проектирования и строительства новых типов быстроходных судов .

Работая на НПП Форма Г. И . Басина организовала в 1994 году Международный Симпозиум по гидродинамике корабля, посвященный 85 –летию выдающегося ученого профессора  Абрама Моисеевича Басина

В 1995 году она перешла на работу в НИЦ Синергетика, где выполнила серию научно-исследователь ских работ, посвященных развитию информационно-волновой теории структур и систем.

Эти исслед0вания Г. И. Басиной были опубликованы в  10 статьях и монографиях 

Синергетика. Эволюция и ритмы человечества.СПб Норма 2003 .260с.

Синергетика. Основы методологии. СПб Норма 2006.56с

Синергетика . Вселенная резонансов. СПб  Норма 2008    144с                         Синергетика . От чисел Басина до Synergonet

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

\                                       Басина Г. И., Басин М. А.

                НИЦ «Синергетика» Санкт-Петербургского союза учёных.

 

5.                                 Синергетика.

           Комментарий к тринитарной методологии Р. Г. Баранцева.

 

 

 

Вот что пишет Р. Г. Баранцев[3]:

«…диада , или бинарная оппозиция, есть элементарная структура анализа. Синтеза на ней не построить. Для синтеза требуется более ёмкая структура. Примеры из естественных наук подсказывают, что следует обратиться, по меньшей мере, к триадам.

Будем называть триадой совокупность из трех элементов, каким-то образом связанных между собой. В зависимости от вида связи различаются следующие типы триад.

Линейные (вырожденные, одномерные), когда все три элемента расположены на одной оси в семантическом пространстве. Например, 1-10-100, дивергенция-параллелизм-конвергенция, левые – центр - правые. Структурно они не богаче, чем диады.

Переходные (гегелевские), характеризуемые известной формулой «тезис-антитезис-синтез». Они лишь провозглашают снятие противоречия, не раскрывая его движущей структуры.

Системные (целостные), единство которых создаётся тремя элементами одного уровня, каждый из которых может служить мерой совмещения двух других. Все три принципиально равноправны.

Особого внимания заслуживает общее семантическое свойство всех системных триад, сложившихся в самых разных системных традициях…

Источник этой закономерности можно видеть в способности человека мыслить одновременно и понятиями, и образами, и символами.

Предлагаемая семантическая формула системной триады

 

                                                             Интуицио

                                                              /          \

                                                   Рацио----------Эмоцио

 

использует понятия, сложившиеся в диадной парадигме, и потому довольно условные. Новое смысловое содержание должно постепенно наполняться по мере их проявления в такой триадической структуре. Перекодировка понятий составляет значительную трудность при любой смене парадигмы. Стереотипы, закреплённые в подсознании, очень трудно вытащить и преодолеть на уровне сознания. Тут не обойтись без «эмоцио» и «интуицио»».

В настоящей работе мы приводим некоторые примеры применения тринитарной методологии при синергетическом исследовании сложных систем.

Если построить системную триаду научного знания [3]:

 

           

 

 

                                                         Философия

                                                          /                 \

                                           Математика------- Конкретные науки,

 

то Синергетика проектируется в центр и приподнята над плоскостью этой триады, становясь её ядром и одновременно осуществляя связи между её элементами. Возникновение Синергетики связано с тем, что в каждом из элементов триады появились возможности для изучения самых сложных проблем науки – проблем самоорганизации материи. Синергетика обобщает эти возможности, и, синтезируя их, порождает новые.

Границы Синергетики лежат в областях её сращивания с элементами триады научного знания, и их установление происходит в творческой конкуренции идей, амбиций и мнений. Задача Синергетики будет выполнена, и границы её будут определены, если триада превратится в полноценную системную тетраду, каждый элемент которой будет иметь своё ядро и связи с другими элементами. Ни попытки уничтожить Синергетику как не имеющую своей сферы исследований, ни противоположные попытки заменить Синергетикой всю базовую триаду научного знания не будут продуктивными.

Значительный вклад в развитие синергетических исследований внесли Санкт-Петербургские учёные. С мая 1993 года по инициативе выдающегося учёного и общественного деятеля В. Д. Поремского в Санкт-Петербурге работал Семинар «Синергетика и методы науки», а с октября 1995 года – функционирует научно-исследовательский центр «Синергетика». Работы центра были поддержаны четырьмя грантами РФФИ (руководитель: проф. М. А. Басин) и тремя грантами РГНФ (руководитель: проф. Р. Г. Баранцев).

                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Д.т.н. профессор Ровинский Реомар Ефимович

 

7.Синергетика . Новое научное направление

 

Разговор о проблемах синергетики начнем с ответа на вопрос, каким образом появилось это новое междисциплинарное научное направление.

Во Второй половине ХХ века возникла необходимость вплотную заняться процессами развития сложных систем, обладающих открытостью, иначе говоря, взаимодействующих с внешней средой, с которой они находятся в состоянии неравновесной необратимости, нелинейности, но на определённом этапе сохраняя внутреннюю квазистационарность благодаря определённым внутренним и внешним взаимодействиям, протекающим на этом этапе развития. В развитии таких систем особый интерес представляют ситуации перехода их в качественно новые состояния. В силу внешних или внутренних причин рано или поздно квазистационарный этап развития нарушается, и все такие системы переходят в неустойчивое состояние, из которого необходим переход в качественно иное, новое устойчивое состояние. Такой кризисный этап завершается переходом системы в одно из возможных устойчивых состояний либо путём частичного или полного разрушения существовавшей упорядоченности, либо, при определённых условиях, достигая более высокую организованность по сравнению с исходным квазиравновесным состоянием.

В 70-х годах ХХ века появилось понимание того, что материя обладает способностью создавать в открытых неравновесных системах состояния, из которых в кризисных условиях могут возникать скачкообразные переходы в качественно новые состояния с более высоким уровнем организации, чем в исходных квазиравновесных состояниях. Иначе говоря, в определенных ситуациях материя проявляет созидательные способности, порождающие в развивающемся Мире новое. Такое свойство, присущее материи, получило название самоорганизации материи. Необратимость и нелинейность протекающих процессов развития, неравновесность сложных систем в определенных условиях порождают, в частности, самоорганизацию материи, обеспечивающую созидательные переходы в качественно новые состояния с нарастающим уровнем организованности.

Классическая равновесная термодинамика рассматривает процессы, протекающие в изолированных системах при отсутствии взаимодействия с окружающей средой. В таких условиях любой процесс преобразования одних видов энергии в другие виды, сопровождаемый совершением работы, завершается необратимыми переходами части участвующей энергии в тепло, которое равномерно рассеивается внутри системы, что ведёт к росту энтропии и достижению ею максимальной величины. Тем самым достигается состояние полного термодинамического равновесия, самого простого состояния данной системы. В дальнейшем происходит распад самой системы.

Открытые сложные системы взаимодействуют с внешней средой, поэтому они выпадают из основных представлений, на которых базируется равновесная термодинамика. В становлении и развитии синергетики, как нового научного направления, важную роль сыграли работы И.Пригожина, создателя нового раздела этой науки, получившего название неравновесной термодинамики [1]. Вторым провозвестником этого направления стал немецкий профессор Г.Хакен, выпустивший через шесть лет после Пригожина свою знаменитую книгу под названием «Синергетика» [2], название которой определило принятое большинством ученых название самого нового научного направления.

С первых же шагов нового научного направления вокруг него возникли серьезные споры. Наряду с достигнутыми положительными результатами ведущихся исследований, диапазон споров не уменьшается. Важно, что до сих пор не удалось создать единую теорию научной синергетики. Нам нет смысла заниматься разборкой этих споров, остановимся на понимании сути нового научного направления  и, возможно, коснемся тех проблем, которые мешают объединить различные научные варианты при нынешнем уровне наших знаний. Итак, перейдём к современной сути синергетики.

В предисловии к своей основополагающей книге «Синергетика» Г.Хакен так определил предмет разрабатываемой им теории: ²Синергетика занимается изучением систем, состоящих из многих подсистем самой различной природы, таких как электроны, атомы, молекулы, клетки, нейроны, механические элементы, фотоны, органы животных и даже люди <...> Мы сосредоточим внимание на тех ситуациях, когда структуры возникают в результате самоорганизации, и попытаемся выяснить, какие причины управляют процессами самоорганизации безотносительно к природе подсистем.² [2].

В точных науках теоретический подход к любому новому явлению считается состоявшимся, если удается создать математический аппарат, способный адекватно отобразить главные закономерности изучаемого феномена. В случае синергетики следует обеспечить математическое описание поведения открытых систем при потере ими устойчивости и скачкообразном переходе в качественно новое устойчивое состояние. Такая задача осложняется тем обстоятельством, что скачок – это крайне нелинейный процесс, при котором малые изменения управляющих параметров вызывают очень сильные изменения состояния системы, ее переход в новое качество. Здесь напрашивается аналогия с фазовыми переходами, ведущими к изменению агрегатного состояния вещества. Процесс перехода начинается при незначительном изменении управляющего параметра вблизи от критической точки. Классическая физика, как правило, стремится иметь дело с плавными, линейными процессами, для описания которых отработан надежный математический аппарат. При слабой нелинейности удается использовать тот же линейный аппарат с поправками на нелинейность. Процессы переходов систем в качественно новые состояния не укладываются в такие рамки, они требуют использования сугубо нелинейного математического аппарата, который в готовом виде отсутствует.

В Синергетике Г.Хакен разработал такой аппарат в виде системы нелинейных дифференциальных уравнений, названных им ²эволюционными уравнениями². Они учитывают роль внешних факторов, толкающих систему к переходу в качественно новое состояние, это потоки энергии и вещества, и роль случайных, непредсказуемых факторов, определяющих ²выбор² одного из возможных устойчивых конечных состояний. Математический аппарат теории очень сложен и пользование им сопряжено с большими и не всегда преодолимыми трудностями.

Первоначально сферой приложения Синергетики была квантовая электроника и радиофизика, области узкопрофессиональных интересов Г.Хакена. Поэтому в качестве примера самоорганизации выберем объект, изучаемый этими дисциплинами, а именно, лазер. Этот квантовый прибор, получивший в последние десятилетия широкую известность, создает высокоорганизованное оптическое излучение. Особенность квантового прибора состоит в том, что процесс самоорганизации реализуется в нём на уровне микромира. Название прибора представляет собой аббревиатуру полного английского наименования, содержащего два ключевых понятия, определяющих принцип его действия: вынужденное излучение и усиление света. Началась эпоха создания оптических квантовых приборов, в которых активную лазерную среду, состоящую из специально подобранных атомов, молекул или ионов, приводят в состояние сильной неравновесности направленным введением специально организованного потока энергии (накачка лазера). В таком состоянии становится возможным избирательное возбуждение активной  лазерной среды до строго определенного уровня. Как только превышается пороговое значение лазерной накачки, в подготовленной среде лавинообразно нарастает вынужденное, а не спонтанное, излучение на строго определенной длине волны. Тогда скачком возникает лазерная генерация узконаправленного почти монохроматичного луча, яркость которого на генерируемой длине волны в миллионы раз превышает яркость любого традиционного источника света. Лазерная генерация есть результат самоорганизации активной среды при выполнении трех перечисленных выше условий: открытости системы, снабжаемой извне энергией, ее крайней неравновесности и превышения порога вводимой в среду энергии. 

Другой подход к математическому описанию физических процессов, сопровождаемых разрывами функций (скачками), разработал Р.Том, использовавший топологическую теорию динамических систем. Им созданы основы теории, получившей название теории катастроф. Существенный вклад в последующее развитие этой теории сделал В.И.Арнольд, благодаря чему стали возможными некоторые важные ее практические приложения. Содержание теории и практические приложения изложены в книге Арнольда [3], предназначенной для нематематиков. Катастрофами называют скачкообразные переходы, возникающие в виде внезапного ответа системы на плавное изменение внешних условий. Соответственно, теория катастроф дает универсальный метод исследования любых скачкообразных переходов, разрывов, внезапных качественных изменений. Самоорганизация – это одно из типичных проявлений подобных событий. Сегодня теория катастроф успешно решает задачи, связанные с определением предельной прочности конструкций, с протеканием циклических химических реакций типа реакций Белоусова – Жаботинского, с поведением волновых фронтов. Однако, серьезные трудности возникают при попытках приложения этой теории к биологическим объектам и социальному сообществу людей. Перспективы теории на будущее в [3] оцениваются так:

“В непосредственном будущем лишь физические науки извлекут из нее (из теории катастроф, Р.Р.) действительную выгоду, поскольку они имеют дело с «простыми» системами, в крайнем случае, со «статистически простыми» системами неорганизованной сложности. Организованная сложность биологии представляется наиболее вероятным объектом изучения на следующем, «промежуточном» этапе, но здесь уже может понадобиться вся теория динамических систем (имеющая теорию катастроф лишь малой, хотя и существенной составляющей). Организованная сложность социальных систем вряд ли будет хорошо понята, пока мы не освоимся как следует с биологическими системами”.

Оба рассмотренных подхода к новому научному направлению (синергетика и теория катастроф) не используют термодинамические представления, поскольку классическая термодинамика имеет дело с изолированными равновесными системами, в которых самоорганизация себя не проявляет. Между тем, термодинамический подход добавляет новые детали, важные для понимания проблемы, поскольку самоорганизация тесно связана с необратимыми процессами, доминирующими во Вселенной. Выяснилось, что именно необратимые процессы играют конструктивную роль в развивающихся открытых неравновесных системах, иначе говоря, в самоорганизующихся системах.

Основоположник новой термодинамики бельгиец Илья Пригожин, удостоенный Нобелевской премии по химии, в своей Нобелевской лекции формулирует проблему так: ²В теоретической химии и физике возникло новое направление, находящееся в самом начале своего развития, в котором термодинамические концепции будут играть еще более важную роль <...> Чтобы разработать термодинамику самоорганизующихся структур необходимо показать, что неравновесие может быть причиной порядка. Оказалось, что необратимые процессы приводят к возникновению нового типа динамических состояний материи, названных мною ²диссипативными структурами² [4].

Под термином «диссипативная структура» Пригожин подразумевает образование некоторой формы супермолекулярной организации, возникающей в результате коллективных действий элементов системы. Для нашей темы наибольший интерес имеют идеологические аспекты теории, излагаемые в [5,6]. Как отмечалось выше, чтобы система могла создавать и поддерживать упорядоченность, она должна быть открытой и получать энергию извне. Оказывается, весь доступный нашему познанию Мир состоит только из таких систем, в развитии которых  прослеживаются два взаимосвязанных этапа, описание которых дано выше.. В развиваемой Пригожиным теории определены критерии, при которых диссипативная система теряет устойчивость, и предсказывается возможное достижение ею качественно новых состояний при скачкообразном выходе из кризиса. Скачок протекает в форме гигантской коллективной флуктуации, при которой многочисленные элементы системы ведут себя согласованно, хотя перед этим их взаимодействие носило хаотический характер.

Представить себе гигантскую коллективную флуктуацию, возникающую в момент скачка, поможет известное в гидродинамике явление, получившее название ячеек Бенара. Если подогревать снизу сосуд, в котором находится жидкость, обладающая необходимой вязкостью, то в его вертикальном сечении образуется перепад температур, вследствие чего возникают хаотичные конвективные потоки. Но как только интенсивность подогрева нижнего слоя жидкости превысит определенное для данной системы пороговое значение, вертикальные потоки скачком перестраиваются и образуют хорошо организованные замкнутые циркулирующие структуры, демонстрирующие высокую степень упорядоченности. Сверху это выглядит так, как будто поверхность жидкости имеет регулярную ячеистую структуру. Картина устойчиво сохраняется все время, пока снизу продолжается подогрев с постоянной интенсивностью. В рамках классических представлений вероятность организации миллиардов и миллиардов молекул жидкости с образованием шестиугольных ячеек Бенара определенного размера практически равна нулю, а если бы даже такое состояние случайно возникло, то упорядоченные структуры сразу после этого распались бы. Но эффект реализуется, он надежно воспроизводится и устойчиво сохраняется, если поддерживаются необходимые условия. Организованное поведение участников эффекта возможно благодаря поступлению извне необходимой для этого энергии. Статистические законы здесь явно не работают, и для объяснения феномена привлекается, в частности, неравновесная термодинамика. По словам Пригожина разработка новой научной дисциплины – неравновесной термодинамики – находится в начальной стадии. Создан ее математический аппарат, но, как и в случае Синергетики, пользоваться им не просто.

Подводя итоги рассмотрения нового научного направления, можно сказать следующее. Вопреки не вполне компетентным высказываниям, что синергетика – не наука, а скорее философия, убедительные факты говорят о том, что это молодая, но пока еще далекая от завершения междисциплинарная наука. Как и у других научных дисциплин, у синергетики есть свой четко определенный предмет изучения, своя методология, она опирается на современное научное знание, у нее есть ряд вполне реальных приложений. С философией ее связывает то, что, как сказал Волькенштейн, «Синергетика – это новое научное мировоззрение, отличное от ньютоновского мировоззрения». Это очень серьезный фактор, выводящий синергетику на роль общенаучной дисциплины. Но на всем протяжении своего относительно короткого существования синергетика сталкивается с серьезными проблемами, которые вызывают брожение мнений в научных кругах. Пока в новом научном направлении действуют, по меньшей мере, три разных подхода, и не видно попыток их объединения. В таких условиях трудно ожидать создания единой теории переходов развивающихся систем в качественно новые состояния. Но основная  трудность создания теории, пожалуй,  носит принципиальный характер: переходные процессы нелинейны, поэтому, хотя Хакен в Синергетике и Пригожин в Неравновесной термодинамике написали уравнения в рамках создаваемых ими теорий, решение таких уравнений в каждом конкретном случае представляет почти непреодолимые трудности. А серьезные критики получают обоснованный повод для утверждения об отсутствии теории, следовательно, и об отсутствии научной дисциплины. Тем не менее, есть основания для оптимизма в отношении будущего синергетики.

Таким образом, попервоначалу синергетика объединяет в своём составе несколько самостоятельных направлений, но это не случайное объединение. В каждом направлении переход открытой системы  в качественно новое состояние происходит только тогда, когда система попадает в кризисный этап своего развития, и такой переход происходит в форме скачка. По этому поводу  И.Пригожин в своей Нобелевской лекции ввел в оборот понятие «точки бифуркации». В синергетике под бифуркацией понимается не математическая точка, а короткий период кризисного этапа, в течении которого заканчивается однозначный эволюционный путь, характерный для предыдущего стационарного этапа развития, и возникает несколько ветвей потенциально возможных выходов из кризиса. Выход осуществляется скачкообразно, а «выбор» дальнейшего пути развития определяется случайным воздействием на систему одной из возникающих на этом этапе флуктуаций. В результате невозможно точно предсказать будущий путь системы после её выхода из кризиса. 

Наряду с тремя рассмотренными нами направлениями, общепризнанно входящими в состав синергетики, возможно появление других направлений, основанных на участии в них новых механизмов самоорганизации материи. Их включение в понятие синергетики обоснуется лишь в случае, когда развивающаяся система попадает в кризисный этап развития, а выход из кризиса и появление качественно нового состояния возникает скачком, но не плавным переходом.  Примеры тому – провалы предпринимавшихся попыток распространить  методы синергетики на биологические развивающиеся системы, а также на людей и человеческие социальные системы. В. Арнольд в теории катастроф уже предупреждал о неготовности современной синергетики распространять свои методы на биологию и социальные системы. Провалы подобных попыток сыграли главную роль в дискредитации синергетики, как междисциплинарной научной дисциплины. Именно здесь идут главные дебаты между сторонниками и противниками этого нового научного направления.

 

 

ЛИТЕРАТУРА

1. Glansdoff P., Prigogine I., Thermodynamic theory of structure, stability and fluctuation,

                                                                                                                        N.Y., Wiley Intercience, 1971

2. Haken H., Synergetic, an introduction. Nonequilibrum phase-transitions and selforganizations in  physics, chemistry and biology. Springer, 1977

3  Арнольд В.И. Теория катастроф. М.: Наука, 1990

4.  Пригожин И. Время, структура и флуктуации (Нобелевская лекция). УФН, 1980, т.131, с.185;

5.  Пригожин И. От существующего к возникающему. М.: Наука, 1985;  Prigogine I. From Being  to  Becoming. W.H. Freeman and Company.  1980

6. Николис Г., Пригожин И., Познание сложного. М.: Мир, 1989;  Nicolis G., Prigogine I  Exploring  Complexity. W.H. Freeman and Company, New York, 1989

 

 

18 марта 2012 года Баранцев Басину

Как Вы знаете, в моей триаде синергетики есть ещё российская школа нелинейной динамики. А у Ровинского она где-то за кулисами. И ни слова о Курдюмове, Малинецком, Буданове, Аршинове. К обсуждению надо подключить Дульнева Г.Н. Всего доброго! Ваш Р.Г.Баранцев.

 

20 марта 2012 года Ровинский Басину

Я готов принять активное участие в готовящемся Вами электронном семинаре. Спасибо за такую инициативу. С кратким откликом Рэма Георгиевича ознакомился. Можете успокоить его, статьи всех перечисленных в отзыве авторов о синергетики я читал, со многим согласен и отношусь к этим работам с должным уважением. А Курдюмову и Малинецкому даже пересылал мою книгу «Развивающаяся Вселенная», где есть ссылка на одну из их совместных статьях по теме книги.  В своей нынешней статье я не ставил своей задачей писать историю развития синергетики, это только выражение моего личного мнения об этом новом научном направлении, изложена сама суть этого мнения. Если возможно, то предлагаю Р.Г. и другим участникам семинара для знакомства с моими сегодняшними научными интересами просто просмотрет ь помещенные на моём сайте материалы по известному Вам адресу:   http://remrovinsky.com

 

 

 

 

 

 

 

 

 

ЧТО ТАКОЕ СИНЕРГЕТИКА

Баранцев Р.Г.

СПбГУ,  СПб

brem@mail.ru

 

    Слово “синергетика” происходит от греческого synergeia – содействие, сотрудничество. В широкое употребление этот термин ввёл немецкий физик Г.Хакен, назвав так новое научное направление, объединяющее исследования по теории самоорганизации. В настоящее время синергетика, преодолевая междисциплинарный статус, превращается в ответственного носителя новой парадигмы. Становясь аттрактором с весьма широкой областью притяжения, синергетика стремится к осознанию имманентных проблем  и уточнению своих границ. Простое название «теория самоорганизации» оставляет желать большей определённости. Следуя семантической формуле системной триады «рацио-эмоцио-интуицио» [1],  мы предложили в [2] такой вариант тринитарной дефиниции синергетики: «нелинейность-когерентность-открытость». Нелинейность может проявляться в самых разных обличиях. Когерентность понимается как такая согласованность взаимодействия элементов, которая проявляется в масштабе всей системы. Открытость подразумевает обмен веществом, энергией и информацией, происходящий в пространстве, времени и масштабе, причём обмен не полностью контролируемый. «То, что полностью контролируемо, никогда не бывает вполне реальным. То, что реально, никогда не бывает вполне контролируемым» [3].

    Компоненты системной триады образуют целостное единство, когда находятся в динамическом равновесии. Проблема определения может быть сформулирована как проблема установления допустимых пределов по каждому измерению системной триады. Эти пределы взаимосвязаны согласно принципу неопределённости-дополнительности–совместности (НДС): каждая пара элементов находится в соотношении дополнительности, а третий задаёт меру совместности. В асимптотической математике, где точность, локальность и простота как элементы определяющей триады имеют количественные выражения, действие этого принципа проявляется наглядно и убедительно [4]. В процессе самоорганизации осуществляется связь структурных уровней разного масштаба, и сам процесс можно рассматривать как вертикальный переходный слой. В таких слоях действуют смешанные языки, рождаются новые смыслы, формируются параметры порядка, регулирующие процесс на системном уровне. Кооперация частей системы с возникновением нового качества, характеризуемого параметром порядка, - это центральная тема синергетики.

    Основное противоречие, которое стремится разрешить синергетика, задаётся оппозицией порядок-хаос. В греческой мифологии слово chaos означало первобытное состояние мира, из которого образовался космос – мир, мыслимый как упорядоченное единство. В современном представлении хаос – беспорядочное, бесформенное, неопределённое состояние вещей, так что антитезой хаосу обычно является порядок. Отчётливо напрашивается вывод, что хаос – это плохо, а порядок – это хорошо. Однако, абсолютный порядок и абсолютный беспорядок одинаково грозят гибелью. При всём стремлении к упорядочению какая-то доля хаоса для жизни необходима. И синергетика как раз раскрывает, восстанавливает позитивную роль хаоса. Оппозиция хаос-порядок разрешается в ней через творчество.

Синергетическая идеология позволяет взглянуть и на общество как на самоорганизующуюся систему, формируя при этом новые концепции в социальных науках. Громадное значение имеет вывод современного естествознания о неоднозначности путей эволюции природных систем, о неустойчивости по отношению к начальным данным. Важно также, что сложным системам нельзя навязывать пути их развития, а нужно обеспечивать самоуправляемое развитие, правильно организуя воздействия в пространстве, времени и масштабе.

    Пространство смыслов - место генерации ведущих признаков, Формируя основные параметры, мысль создаёт структуры как устойчивые комплексы связей в пространстве отношений. В поисках наиболее общих закономерностей мысль абстрагируется от конкретного содержания и остаётся в пространстве чистых отношений, структурные формы которых определяют план организации. Символизируя глубинные архетипы, эти структуры видятся как знаки и, становясь понятиями, обретают смысл параметров порядка. Знаковый подход – прерогатива семиотики. Однако в процессе самоорганизации происходят качественные изменения, для обозначения которых требуются динамические структуры, т.е. семиодинамика.

Семиодинамика, как и синергетика, занимается изучением механизмов синтеза целостных образований. Однако судьба их сложилась по-разному. Семиодинамика, рождённая в своём отечестве, не нашла понимания и признания, а синергетика, изобретённая за рубежом, стала восприниматься, как новое направление, способное возглавить смену парадигмы. История не слишком оригинальная, но в очередной раз пройденная и достаточно поучительная в своих деталях, тем более, что сохранились документальные свидетельства этих не столь уж давних событий [5]. В России семиодинамика оказалась предтечей синергетики. Когда Г.Хакен ставил вопрос о существовании общих принципов самоорганизации независимо от природы отдельных частей системы, этот вопрос, по его собственному признанию, звучал тогда как-то неестественно и казался «притянутым за уши» В России критическая масса была достигнута лишь в 1983 году на конференции в Пущино, как раз в то время, когда семиодинамика уже успела заслужить обвинение в идеологической вредности и своим упорным сопротивлением измотала идеологические власти, значительно их обессилив. Тем самым она сыграла роль штрафной роты, очистившей минное поле предубеждений перед наступлением синергетики.

Популярность синергетики угрожает размыванием её берегов, так что сама она всё больше нуждается в русле достаточной определённости, и предмет этой науки обязывает её к самоопределению. Однако взгляд изнутри недостаточен для целостной идентификации. А извне на роль параметров, характеризующих синергетику, предлагались пока слишком широкие и обречённо негативные показатели: нелинейность, неустойчивость, незамкнутость,… Выход в новое всегда начинается с отрицания, отказа, освобождения от старого. Поэтому новое обычно определяется апофатически: неэвклидовы геометрии, неклассическая физика, неравновесные процессы и т.п. Попытки экстраполяции обречены на встречу с парадоксами, катастрофами, сингулярностями, которые плодотворны постольку, поскольку обозначают место формирования внешних границ. Поиски границ синергетики в пространстве методов выводят на принцип НДС, формирующий внутреннюю меру, которая проявляется через обобщённый параметр Планка, оберегающий целостность системы. Сопоставление асимптотики и синергетики обнаруживает их родство по динамизму методов: от предела – к приближению, от бытия – к становлению, от полноты – к целостности. Будучи предтечей синергетики, семиодинамика сумела заложить основы структурной методологии, которая помогает синергетике определить свои берега и обрести подлинное русло. Обживаясь в нём, синергетика вскоре возможно не удивится, осознав себя семиодинамикой./

 

1.   Баранцев Р.Г. Становление тринитарного мышления. М.-Ижевск, 2005, 124 с.

2.   Баранцев Р.Г. Имманентные проблемы синергетики // Новое в синергетике: Взгляд в третье тmысячелетие. М.: Наука, 2002. С.460-477.  В-сы философии, 2002, №9. С.91-101.

3.   Пригожин И., Стенгерс И. Время, хаос, квант. : Либроком, 2009,232 с.

4.   Андрианов И.В., Баранцев Р.Г., Маневич Л.И. Асимптотическая математика и синергетика: путь к целостной простоте. М.: Едиториал УРСС, 2004, 304 с.

5.   Баранцев Р.Г. История семиодинамики: Документы, беседы, комментарии. М.-Ижевск: РХД, 2006,380 с.

 

 

 

              9.Дф-м наук                        Ланда Полина Соломоновна

Нелинейные колебания и волны.

Москва. Наука. Физматлит.

1997

496 страниц.

 Введение

1.   Основное содержание книги.

 Назначение предлагаемой вниманию читателей книги состоит в том, чтобы дать представление о современном состоянии теории нелинейных колебаний и волн. отличительной её особенностью является единый подход как к колебательным и волновым явлениям, так и к регулярным и хаотическим процессам в динамических системах. Такой подход ведёт начало от работ Л.И. Мандельштама. В частности, он отражён в знаменитом курсе лекций Мандельштама по теории колебаний [224], созданном им самим и прочитанном впервые на физическом факультете Московского Государственного университета в 1930 году.

 

Книга состоит из введения , четырёх частей и двух приложений. …

 

2.   Определение и значение теории колебаний и волн , предмет её исследования.

Теория колебаний и волн (входящая в настоящее время в состав Синергетики) – это наука, изучающая колебательные и волновые движения независимо от их физической природы. Под колебательными движениями мы , согласно Л.И. Мандельштаму ,  будем понимать всякие происходящие длительное время ограниченные изменения состояния тела. В силу ограниченности эти изменения обязательно должны происходить «туда и обратно»[224]. Под волновыми движениями мы будем понимать колебательные движения, распространяющиеся в пространстве. Из этих определений уже видно, что изучение колебательных и волновых движений должно быть взаимосвязано, т.е. разделение теории колебаний и теории волн не является оправданным. Данное определение теории колебаний и волн является очень широким. Ведь и другие науки тоже изучают изменение состояния тел во времени и пространстве. Чем же отличается  от них теория колебаний и волн? Ответ на этот вопрос дан Л.И, Мандельштамом [224] . Если другие науки интересуются в первую очередь тем, что происходит с телом в данном месте  и в данное время, то теория колебаний и волн интересуется «общим характером процесса, взятого в целом , за большое время»

    Весьма интересно, что существуют общие закономерности колебательных и волновых движений, не зависящие от конкретного вида системы. Все эти закономерности чётко ещё нигде не сформулированы, но многие исследователи часто  полуинтуитивно, ими пользуются в своих работах. Зная эти общие закономерности, можно упешно предсказывать различные явления в самых разных областях науки. Классическим примером такого предсказания является открытие Л.И. Мандельштамом комбинационного рассеяния света [219][220], которое первоначально предсказано им , исходя из аналогии между этим явлением и нелинейным взаимодействием колебаний с различными частотами. Об аналогии между комбинационным рассеянием и привычными объектами теории колебаний Мандельштам писал следующее. [225]: «С точки зрения теории колебаний беспроволочная телефония и комбинационное рассеяние света одно и то же. Это модуляция. Звук - в радио, колебания атомов – в модуляционном рассеянии». Таким образом, основой предсказания является наличие аналогий между колебательными и волновыми системами различной физической природы. О таких аналогиях в одной из лекций по теории колебаний Мандельштам сказал, обращаясь к слушателям [225]: «Все вы знаете такие системы как маятник и колебательный контур , и знаете, что это с колебательной точки зрения одно и то же . Теперь всё это тривиально, но замечательно именно то , что оно тривиально». Эти слова не устарели до сих пор. Однако, приведённые примеры не отражают полностью общности законов теории колебаний, поскольку маятник и колебательный контур описываются уравнениями одного и того же  вида. Можно привести другой, более современный пример, иллюстрирующий эту общность. Рассматривая одномерное отображение типа параболы (так называемое логистическое отображение, молодой американский математик М. Фейгенбаум открыл ряд закономерностей для последовательности бифуркаций удвоения периода (см. гл. 12) и получил некоторую константу, которая затем получила название константы Фейгенбаума. Впоследствии оказалось, что эти закономерности справедливы для весьма широкого класса систем, которые описываются самыми разными уравнениями, и что найденная Фейгенбаумом константа является универсальной. [398, 314]. Более того, универсальным оказалось даже поведение спектров при таких бифуркациях.[399]

 

Лекции и семинары Л.И. Мандельштама носили особый характер. А.А. Андронов писал в своей статье: «Л.И. Мандельштам и теория нелинейных колебаний» [6] «Лекции и семинары (Л.И. Мандельштама) всегда содержали новые научные результаты , которые нигде больше не публиковались. Но, может быть, ещё большее значение этих лекций было в систематическом развитии навыков колебательного мышления, в общем повышении колебательной культуры. К сожалению «колебательной культуры до сих пор не хватает многим, даже весьма крупным, специалистам, занимающимся конкретными научными исследованиями. Так, если бы химики в своё время обладали такой культурой, то они бы не заявляли о принципиальной невозможности колебательных химических реакций в гомогенной среде, и судьба Б.П. Белоусова, открывшего в 1951 г. эти реакции экспериментально[35], возможно, сложилась бы иначе ( Сомнения относительно возможности существования колебательных химических реакций исчезли после публикации книги А.М. Жаботинского.[110] ).

Кроме того, до сих пор время от времени появляются научные работы, совершенно ошибочные с точки зрения теории колебаний. Обладай их авторы знанием законов этой теории, указанные работы могли бы и не появиться.

    Исторически получилось так, что теория колебаний в начальный период своего формирования в самостоятельную науку больше всего тяготела к радиотехнике, черпая из неё свои модели и объекты исследования. В силу этого понимание общности законов теории колебаний, необходимости их изучения специалистами различных областей науки, пришло далеко не сразу, если вообще пришло. Не случайно, например, на физическом факультете Московского государственного университета курс теории колебаний читается только на отделении  Радиофизики.

 

Предмет исследования теории колебаний и волн.

          

Наличие аналогий между колебательными и волновыми явлениями в системах различной природы является причиной того, что теория колебаний и волн получила свой предмет исследования, т.е. стала самостоятельной наукой. Таким предметом  является динамическая система, а именно, система, поведение которой задаётся некоторым набором правил (алгоритмом) [249, 258].В  частности, и это наиболее часто, поведение динамической системы описывается уравнениями – дифференциальными, интегральными или конечно- разностными. Очевидно, что динамическая система представляет собой лишь модель какой-либо реальной системы. Любая реальная система подвержена флуктуациям, как внутренним, так и внешним, и потому не может быть динамической. В силу этого можно сказать, что теория колебаний и волн изучает не конкретные системы, а их абстрактные модели. Об основных моделях теории колебаний и волн , их роли и классификации речь пойдёт в части 1.

Если в физике динамические модели исследуемых явлений составлялись и изучались давно, то в других науках этого, как правило не было. Изучение было конкретным. И , в основном, чисто описательным. Только в последние десятилетия положение существенно изменилось. Модели стали составляться и исследоваться в химии, биологии, экологии, метеорологии, экономике и даже медицине. Исключения, правда, встречались и раньше. Так, А.Лотка в 1920 году предложил математическую модель гипотетической химической реакции, в которой возможны колебания концентраций реагирующих веществ[520-521]. Аналогичная модель была затем предложена Вольтера[632, 79] для объяснения колебаний численности конкурирующих видов животных и растений. Эта модель получила название «хищник-жертва». В 1928 г. Б. Ван-дер-Поль в соавторстве с М. Ван –дер-Марком предложили динамическую модель сердца в виде трёх связанных генераторов [629]

C помощью этой модели авторы демонстрировали некоторые известные заболевания сердца, например, аритмию, и даже пытались предсказывать новые заболевания. Но подобных моделей было чрезвычайно мало, и они, как правило, оставались неизвестными широкому кругу исследователей.

Анализируя динамические системы, являющиеся моделями различных реальных систем из самых разных областей науки , можно обнаружить в них много общего. В результате эти системы можно классифицировать по тому или иному признаку и для каждого класса выделить наиболее типичные. Такая классификация, играющая немалую роль при изложении теории колебаний и волн, будет проведена в гл. 1.

3.   История создания и развития теории колебаний и волн.

Как и когда возникла такая обобщающая наука, как теория колебаний и волн? Повидимому её началом следует считать труды Лагранжа в области аналитической механики, опубликованные им в 1788 году. Введя обобщённые координаты и импульсы, Лагранж, в сущности, отошёл от традиционной механики и записал динамические уравнения, которые могут быть отнесены к системам любой природы. Исследование свойств решений этих уравнений позволяет получать общие колебательные и волновые закономерности. Не случайно, в современной литературе по колебаниям и волнам многие фундаментальные идеи излагаются на языке классических уравнений Лагранжа (или их эквивалента – канонических уравнений Гамильтона).

Важнейший этап в создании теории колебаний и волн связан  струдами Релея (Дж.Стретта), вышедшими в 1877 году в виде книги под названием «Теория звука»[304]. В этой книге Релей впервые обратил внимание на аналогию между акустическими и электрическими колебаниями. Хотя , в основном, книга посвящена линейной теории колебаний  и волн, в ней уже заложены основы нелинейной теории, в частности, теории автоколебаний. Было выведено уравнение , отражающее основные  закономерности процесса автоколебаний и носящее в настоящее время имя Релея. Многие задачи, поставленные в книге Релея, получили решение значительно позднее.

К ним относится, например, исследование автоколебаний так называемого маятника Фроуда [300] , исследование термозвуковых колебаний в резонаторе Гельмгольца  

    

Литература.

224.Мандельштам Л.И. Лекции по колебаниям. Собрание трудов, т.4 Москва: изд-во  АН СССР. 1955.

219/ Мандельштам Л.И. «Новое явление при рассеянии света» Собрание трудов.т.1 Москва: изд. АН СССР. 1947,сс293-296

220 Мандельштам Л.И. «О рассеянии света в кристаллах» Собрание трудов.т.1 Москва: изд. АН СССР. 1947, сс305-317

225. Мандельштам Л.И. Лекции по оптике, теории относительности и квантовой механике.  Москва: Наука. 1972.

398. Feigenbaum M.J.”Quantitative universality for a class of nonlinear transformations, J. Stat. Phys.,1978,v.19,N1, pp.25-52.

314. Фейгенбаум М. «Универсальность в поведении нелинейных систем.» УФН, 1983. т.141,в.2,СС.343-374.

399. Feigenbaum M.J.”The onset spectrum of turbulence” Phys Lett.1979, v.74A, No6, pp.375-378.

6. Андронов А. А. Собр. Трудов.Москва: Изд-во АН СССР, 1956.

35.Белоусов Б.П. «Периодически действующая реакция и её механизм. В сб. рефератов по радиационной медицине. Москва: Медгиз, 1959, СС.145-148; Химия и жизнь, 1982, №7,сс65-68

110.Жаботинский А.М. Концентрационные колебания. Москва: Наука, 1974

249.Неймарк Ю.И. «Теория колебаний вчера и сегодня», Динамика систем (Качественно-численное исследование динамических систем) Горький: Изд-во ГГУ, 1988, СС.34-53

538. Neimark Yu. I .”Some problems of the qualitative theory of vibration”, Advances in mechanics 1991,v.14,No.3,pp.102-104 -

520. Lotka A.J. “Undamped  oscillations derived from the low of mass action”, J. Amer. Chemical Society, 1920, v.42, No ,8,pp.1595-1599.

521. Lotka A.J. Elements of Physical Biology. Baltimora,  1925.  

632. Volterra V. Leçons sur la Theorie Mathematique de la Lutte pour la Vie.Paris: Gauthier-Villars 1931.

 79. Вольтерра В. Математическая теория борьбы за существование. Москва: Наука, 1976

304.Стретт Д.В.(Релей) Теория звука. Т1,2. Москва: Гостехиздат,1955

300. Стрелков С.П. «Маятник Фроуда», ЖТФ, 1933,т.3,в.4,Сс.563-570.

 

 

 

 

 

 

 

 

 

 

 

 

 

    

                                                                Этюд 1 

Три языка Синергетики

.

 

1.   Выделение объекта исследования.

Создание его мысленного образа.

 

Объектом исследования обычно является некоторая структура или система (совокупность связанных между собой структур), которая может быть выделена из окружающей природы и в течение некоторого времени сохраняет собственную индивидуальность, то есть частичную или полную независимость от окружающей среды (поля).

Целостная структура может быть охарактеризована одним словом, названием объекта. Название объекта ассоциируется в человеческом мозгу c первоначальным образом объекта, сложившимся на основе визуальных, звуковых и других типов ощущений, связываемых в единое целое. При этом формирование образа объекта на основе одной и той же полученной информации может явиться бифуркационным. Неоднозначным является также соответствие между названием объекта и его образом. Выделяя объект из природы, на основе обработки полученной нами информации, мы составляем в мозгу его образ, даем ему имя и можем ввести два числа: единица и нуль, - характеризующие соответственно существование и отсутствие объекта.

 

2.   Использование трёх языков синергетики.

 

Тем самым, мы вводим в рассмотрение три языка синергетики и науки вообще:

а) язык образов,

б) язык слов,

в) язык математики [1].

Язык образов позволяет нам получить общее представление о красоте и многообразии окружающего мира и о взаимодействии объектов между собой.

Язык слов помогает отметить очень важную особенность окружающего мира, позволяющую строить его научную картину, - существование объектов, во многом идентичных друг другу, которые могут быть названы одним словом.

Язык математики позволяет уже на первой стадии рассмотрения  ввести логистическую математическую группу [3], описывающую отсутствие, рождение, существование и гибель выделенного объекта.

 

3.   Проведение лингвистического анализа.

 

Название и, если это возможно, словесное определение объекта, позволяют включить в процесс исследования язык слов, каждое из которых является символьным обозначением широкой совокупности различных объектов,  и тем самым подключить к исследованию все те возможности установления глубинных связей изучаемой структуры или системы, которые существуют в человеческом языке, несущем в себе в символьном виде всю историю человечества.

Переводы названия объекта на другие языки, отыскание близких по смыслу слов позволяют построить поле слов и соответствующих им объектов, так или иначе связанных с изучаемой нами системой или структурой. При этом уже на этой стадии исследования выявляются скрытые первоначально связи объектов и явлений.

 

4.   Предварительная классификация процесса или объекта. Включение процесса (объекта) в систему квант- волна.

                 

    Этот пункт исследования является наиболее важным на первом этапе исследования, так как позволяет ввести масштабную (в обобщенном, не только геометрическом, смысле) иерархию, включающую в себя объект исследования.

    В основу этой классификации положен тот не до конца объясненный экспериментальный факт, который, по-видимому, является проявлением фундаментального закона существования волновых систем и позволяет их научно исследовать, что большинство объектов или процессов не существуют в единственном числе, а образуют группы или классы идентичных или почти идентичных объектов или процессов.

     Именно это свойство является, по нашему мнению, основанием, позволяющим человеку познавать себя и окружающую среду, предсказывать и в некоторой мере управлять будущими событиями и выживать в бурно меняющемся Мире.

    Структуры или процессы, входящие в совокупности идентичных или почти идентичных объектов, называются нами «квантами» (по аналогии с квантовой механикой), а совокупности идентичных или почти идентичных объектов – обобщенными волнами.

    Любая сложная информационно-транспортная система, состоящая из большого количества элементов и имеющая в Природе некоторое количество аналогов, может одновременно рассматриваться и как квант, и как обобщённая волна. По отношению к своим элементам - квантам она является обобщенной волной, а по отношению к совокупности систем, аналогичных данной – квантом. Тем самым в природе существует масштабная иерархия обобщённых волн – квантов, простирающаяся как в сторону больших, так и в сторону малых масштабов, что позволяет в некоторых случаях искать общие закономерности в соотношениях между обобщёнными волнами и квантами.

    Вот как пишет об этом свойстве природы П. Тейяр де Шарден.[2]

    « Но чем больше мы искусственно расщепляем материю, тем больше выступает её фундаментальное единство. В своей наиболее несовершенной, но в наиболее легко представляемой форме это единство выражается в удивительной схожести обнаруженных частиц. Молекулы, атомы, электроны – все эти крошечные тельца, каковы бы ни были их величина и название, являют собой (по крайней мере, на том расстоянии, с которого мы их наблюдаем) полное тождество по массе и поведению. По своим размерам и действиям они кажутся удивительно стандартными и однообразными…»

Иерархия волн - квантов обычно имеет в некотором диапазоне масштабов масштабно - подобный (квазифрактальный) характер и практически всегда может быть линейно продолжена как в сторону увеличения, так и в сторону уменьшения масштабов.

При этом каждый уровень иерархии может быть рассмотрен как волна и как квант, в зависимости от масштаба рассмотрения.        Таким образом, при  рассмотрении сложной самоорганизующейся системы мы можем в качестве одной из обобщённых координат рассматривать иерархию квантов – волн.

 

5.   Словесная история объекта.

 

    Всякая сложная структура или система взаимодействует с окружающей средой (полем) и, трансформируясь в процессе этого взаимодействия, сохраняет те некоторые основные параметры (инварианты), которые позволяют считать её (да и ей осознавать себя - в случае наличия у нее сознания) именно данной системой. Это свойство системы обычно называют целостностью.

     Тем самым исследование самоорганизующихся систем должно выполняться как историческое исследование, должна быть выстроена последовательность событий, в которых участвует данная система.

    Первым этапом такого динамического исследования должна быть словесная история объекта, включающая в себя описание в хронологическом порядке последовательности наиболее существенных для данной системы событий. Такое описание может выполняться параллельно с другими этапами исследования системы и развиваться по мере поступления новой информации о системе.         Оно также может дать материал для анализа и качественного предсказания возможных путей развития объекта.

    Уже на первых этапах исследования язык слов позволяет нам вместо сиюминутного изучения системы в данный момент изучать качественно её динамику как процесс, вводя в рассмотрение «абсолютное время» окружающей среды (поля) и внутреннее время изучаемого нами процесса (последовательности изменений, происходящих в изучаемой нами системе). 

    В последнее время, благодаря развитию кино, телевидения и компьютерной графики, у нас появилась также возможность осуществлять образное моделирование развития или разрушения структур и систем, то есть описывать и фиксировать в образах динамику их изменения. В этом случае происходит сближение образного языка науки с языком искусства. Этот процесс открывает новые возможности в создании принципиально новых синтетических средств описания явлений природы и общества на грани науки и искусства. 

    На этом этапе  мы должны рассмотреть  глубокую проблему времени, имеющего как минимум две ипостаси:

-       время как параметр, изменяя который мы следим за изменением структур (систем ) и полей;

-       время как одна из обобщенных координат при исследовании изменения структур и окружающей среды (процессов)

    Одной из важнейших проблем синергетики [6] и науки вообще является проблема обратимости времени, полное решение которой не получено и вряд ли будет получено когда-либо. Хотя становится очевидным, что частичное решение этой проблемы связано с  бифуркационными событиями и процессами, процессами перезамыкания границ, формированием ударных волн, хаотизацией, с такими понятиями, как энтропия, информация, управляющий механизм (контроллер), и даже с проблемами симметрии, расширения и сжатия Вселенной [7], и что самое удивительное, с проблемой Сознания.[8] 

    Другой философской и математической проблемой, связанной с временем, является проблема его дискретности и непрерывности и возможностей перехода от его дискретного введения к непрерывному.

                                                     

 

 

Этюд 2.

 

Параметр целого.

 

 

1     Выбор основной меры характеризующей объект. ( параметра целого),

 

Этот творческий процесс является наиболее важным для перехода от образного и словесного описания к математическому. Любая целостная система, которая может быть описана одним словом и порождает единый образ, должна иметь некую действительную скалярную меру - параметр целого,- изменение которого описывает процесс возникновения, развития системы и ее взаимодействия с окружающим миром. Выбор этого параметра с целью построения  математической модели системы не является однозначным, так как сложные системы могут быть описаны большим (а иногда бесконечным) числом обобщенных координат. Удачный выбор параметра целого, характеризующего систему и соответствующий ей процесс, является следствием того мысленного образа изучаемого объекта, который сложился на предыдущих этапах исследований. Параметр целого должен быть выбран таким образом, чтобы он легко измерялся или вычислялся и характер зависимости его от времени был устойчив и близок для ряда аналогичных систем.

Науке нужно не точное знание о природе, а шарж, охватывающий основные характерные черты изучаемых ею объектов и процессов. Это связано с тем, что научные данные – это проверяемые опытом данные, то есть повторяющиеся в том или ином виде у различных квантов данной обобщённой волны. Чем более сложен объект научного исследования, тем больше в нем индивидуального, тем меньшее число частных особенностей предмета может быть научно исследовано.

Если мы оставляем при научном исследовании сложного объекта лишь одну обобщенную координату (меру, параметр целого, параметр Планка), то в качестве неё можно использовать величину, каким-либо образом характеризующую объем математического многообразия, описывающего систему. Это может быть действие, энергия, масса системы, энтропия или информация, реальный геометрический объем, количество входящих в нее элементарных подсистем, это, наконец, может быть количество денег, обращающееся в экономике, прибыль корпорации, количество слов в языке и даже переменная возможность существования самой системы.

В качестве основной рекомендации, которая может быть дана при исследовании систем, являющихся обобщенными волнами в нашем понимании, предлагается принять за параметр целого изучаемого объекта число элементов - квантов, которые включены в объект как в обобщенную волну, или, если каждый из них имеет свою меру или параметр целого и эти меры аддитивны, то суммарную меру всех квантов, включённых в систему .

 

Выделение параметра целого подразумевает огромное информационное сжатие, то есть идентификацию квантов, включённых в систему как в обобщённую волну..

 

Отметим, однако, что параметр целого  не полностью определяет динамику исследуемой структуры или системы. В действительности, в некоторых случаях отдельные части системы могут воздействовать на изменение этого параметра и близкие по типу системы на одном и том же этапе развития могут иметь, хотя и не сильно, но отличающиеся друг от друга значения этого параметра.

Задачей исследователя является такой выбор этого параметра, чтобы динамика его изменения мало варьировала у систем как квантов, включаемых в одну волну.

Обычно важное различие между параметром целого другими обобщёнными координатами состоит в разных временных масштабах их изменения. Параметр целого изменяется на большем масштабе времени, чем подчиненные ему части //(обобщённые координаты) системы и более устойчив к внешним возмущениям. В некоторых случаях параметр целого может характеризовать качественную характеристику системы и различие в этих параметрах для сравниваемых систем определяет превосходство одной системы над другой

 

 

2.         Простейшая форма математического описания объекта.

 

    Простейший наиболее схематический вид описания структуры с помощью параметра целого, соответствующий логическому подходу, состоит в представлении динамики объекта в виде двух чисел 0 и 1, где 0 соответствует отсутствию структуры, а 1 - ее существованию.

Можно ввести в рассмотрение простейшую математическую группу –логистическую.

Введём групповое умножение.

0*1=0- ликвидация объекта;

1*0=0-подтверждение отсутствия объекта;

0*0=1 – рождение объекта;

1*1-1- подтверждение существования объекта.

{0,1}-коммутативная группа (то есть группа, в которой операции умножения перестановочны), описывающая существование объекта.

На этом уровне уже можно построить фазовую прямую,на которой фазовая траектория описывается в виде двух направленных отрезков прямых, отрезка [0,1] и отрезка [1,0].

Если взаимно однозначно отобразить группу [0,1] на группу    [-1,1] -, являющуюся группой зеркальной симметрии, то мы можем установить относительную эквивалентность существования или отсутствия объекта с его тождественностью самому себе  и зеркальным отображением.

   

 

 

 

3. Рождение и разрушение объекта.

 

    Если ввести в рассмотрение время как изменяющийся параметр, то всякий объект должен иметь начало и конец во времени, а следовательно, какой-то период существования.

    Предположим, что до момента  объекта не существовало. Параметр целого данного объекта равнялся нулю. В момент  произошло рождение объекта, который просуществовал до момента времени , после которого он исчез. Даже такое простейшее эволюционное рассмотрение позволяет ввести ряд математических  понятий.

1. Момент рождения объекта ,

2. Момент разрушения - исчезновения объекта или его превращения в новый объект ,

3. Срок жизни объекта  - период существования объекта. -

4. Возможное число реализаций объекта за единицу времени

5. Потенциальная частота реализации объекта.

    Конечно, можно мыслить себе вечные структуры, однако, весь опыт жизни подсказывает, что вечных структур нет.   Поэтому при нашем рассмотрении в качестве аксиомы можно принять гипотезу о том, что все структуры имеют начало и конец во времени, имеют какую-то длительность существования.

    Правда, при этом в большинстве случаев гибель (разрушение) структуры может приводить к появлению одной или нескольких новых структур или систем, и с этой точки зрения сам процесс формирования новых и разрушения старых структур может считаться бесконечным. Такой подход конструктивен, так как позволяет прослеживать дерево генетических связей структур и систем. Однако, и в этом случае бесконечность самого процесса можно подвергнуть сомнению.

    Если мы рассматриваем множество идентичных структур (квантов) – обобщённую волну, то подобный подход позволяет нам вводить в рассмотрение определённые типы распределений, связанные с числом структур, их моментами рождения и гибели и длительностью и частотой их существования.

    Введение аксиомы конечности времени существования реальных объектов ставит следующие вопросы:

 

Что такое рождение структуры (системы)?

Что такое разрушение (гибель) структуры (системы)?

 

    При первичном (простейшем) рассмотрении можно считать, что структура рождается и исчезает мгновенно. Вот её не было (0) и вдруг она возникла (1) и наоборот - вот структура была - вот уже её нет .

    В этом случае можно осуществить простейшее графическое описание динамики объекта в виде графика зависимости параметра целого от времени. Этот график представляет собой три отрезка прямых.

 

 

 

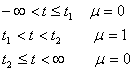
График этой зависимости   мы называем «шляпкой в виде цилиндра»!, соответствующей данному объекту. Здесь, наряду с математическим, мы используем образный (график) и словесный (название этого графика) языки синергетики.

    Если процесс существования объекта рассматривать как непрерывный, то в моменты возникновения и разрушения структур в природе должны происходить качественные изменения (ведь рождается (или исчезает) нечто новое).

    Большинство существующих научных теорий описывает взаимодействие уже существующих структур. Вопрос же об их возникновении и разрушении не имеет в настоящее время полного решения.

    Однако, при первичном исследовании конкретного объекта целесообразно начинать с рассмотрения именно этого вопроса, тем более, что во многих случаях именно его решение представляет наибольший практический интерес.

    В простейшем рассмотрении мы считали, что рождение и исчезновение структуры происходит мгновенно. Это достаточно сильное допущение, хотя во многих случаях мы наблюдаем действительно очень быстрое формирование новых структур и разрушение старых.

    Не напрасно в человеческом языке существуют такие слова, как катастрофа, кризис, взрыв, революция, рождение, разрушение, удар  и т.д.

    Однако как бы быстро ни происходило в некоторых случаях формирование новых структур, всё равно это процесс, имеющий ту или иную протяжённость во времени.

    В некоторых случаях процесс формирования структур может оказаться достаточно длительным.

    Какие же изменения в рассмотренном нами подходе можно ввести, если учесть указанные обстоятельства?

    Вместо мгновенного формирования структуры и мгновенного её разрушения необходимо рассматривать конечные периоды возникновения и разрушения структуры. Это вполне естественное допущение влечёт за собой ряд следствий.

    Первое следствие состоит в том, что возникает вопрос, а что же происходит со структурой в эти периоды? Существует она или нет? Ответ на этот вопрос совсем не тривиален. По-видимому, в периоды рождения и разрушения про структуру нельзя с полной определённостью сказать ни то, что она существует, ни то, что её нет. Если всё же считать процесс формирования структуры непрерывным, без выбросов, то точки 0 и 1 нашего графика вблизи точек  и  можно соединить плавной кривой. «Шляпка» из «цилиндра» превращается в «мягкую шляпу».

    Как же интерпретировать эту кривую?  В период рождения уже нельзя сказать, что структура не существует, но ещё нельзя сказать, что структура уже полностью оформлена.        Понятие степени существования структуры существенно отличается от классического представления о вероятности того или иного события, имеющего несколько возможных исходов и реализуемого большое число раз, которое будет рассмотрено ниже. Здесь понятие степени ближе к представлению о мере. Что может означать в каждом конкретном случае степень существования структуры, равная 0.5?

    На этом уровне рассмотрения попытка интерпретации введенного нами параметра оказывается не вполне корректной. По-видимому, такая интерпретация должна быть сделана в каждом частном случае отдельно с учетом эмпирических данных и того “физического смысла“, который должен вкладываться в понятие параметра целого, описывающего структуру.

Попытаемся указать путь возможного решения этой задачи с другой стороны – от обратного. Мера, характеризующая произвольную структуру, может быть получена как объём многообразия, формирующегося обобщёнными координатами, которые её характеризуют при более детальном описании (смотри ниже). Этот объём может меняться в процессе времени существования структуры. Если структуры нет, то нет и многообразия, ее описывающего. В процессе существования (функционирования) структуры существует какой-то промежуток времени, когда многообразие, описывающее структуру, имеет максимальный объём. Если объём многообразия, описывающего структуру  в любой момент времени, поделить на его максимальное значение, то получим в наиболее естественном случае ту самую «шляпообразную»  кривую, которую мы построили ранее из других соображений и форму которой мы ищем. (естественно, что это не единственная возможность графического представления параметра целого, однако в большом количестве случаев рассматриваемых структур и систем именно такой график является характерным.),.

В случае, если изучаемая нами структура в течение длительного времени остаётся стабильной и сохраняет фазовый объём соответствующего ей многообразия, а в периоды возникновения и разрушения резко его изменяет, то  её параметр целого может быть отождествлён с объёмом многообразия, её описывающего.

    Рассмотрим первоначально некоторые общие закономерности, связанные с этапом рождения структуры. Как следует из той информации, которую мы получаем при изучении природы, можно рассматривать несколько способов рождения новых стр/уктур.

 

а) Появление новой структуры (обобщённой волны) вследствие объединения или самоорганизации структур более низкого уровня иерархии, имеющих меньший объём и размерность описывающих их многообразий (квантов).

б) Появление новой структуры (новых структур) в результате деления аналогичной структуры на две и более частей.

в) Появление новой структуры или нескольких новых структур вследствие потери устойчивости структуры, существовавшей до их образования

г) Рождение новой структуры в результате слияния двух родственных структур с возможным переходом затем к многократному использованию  второго способа.

д) Рождение новой структуры или волны путем излучения структур более высоких классов.

е) В качестве отдельного способа может рассматриваться целенаправленное формирование новых структур структурами более высокого класса (творчество)

 

Способы рождение новых структур в биологии блестяще описаны Тейьяром де Шарденом.[19,стр. 90] .

 

Большинство описанных способов  приводит к необходимости анализа процесса формирования новых структур как бифуркационного изменения старых, уже существовавших ранее систем и структур . Тем самым, процесс появления и разрушения структур включается в, возможно, бесконечную цепочку превращений одних структур в другие – именно здесь можно ожидать появления в окружающем нас мире бесконечностей, если они вообще существуют.

 

Если в качестве основного структурообразующего параметра согласно Тейяру де Шардену [19] принять время, то можно проследить не только время существования той или иной структуры, но и построить во времени математическое  дерево (а в более общем случае граф ) появления, существования и разрушения структур, проанализировав при этом не только внешние связи структуры с окружающей средой: полем, но и генетическую связь структур между собой .

    Многие структуры после своего появления начинают изменять свои основные обобщённые координаты, не меняя, например, числа обобщённых координат приближенно описывающего их многообразия. В качестве примеров можно привести :

 

а)  рост амплитуды морской волны при приближении её к берегу;

б) рост парового пузырька или паровой каверны при увеличении скорости движения тела;

в) рост кристаллов в растворе;

г) рост атомного гриба;

д) рост биологической клетки после деления;

е) рост живого организма;

ё) рост числа научных исследований в новой отрасли знаний,

ж) рост количества людей.

    Таким образом, вновь сформировавшаяся структура в некоторых случаях может после своего появления в течение некоторого промежутка времени интенсивно увеличивать объём описывающего её многообразия, а следовательно и параметра целого, пока не выйдет на некоторое квази-стационарное состояние.

Это квазистационарное состояние можно характеризовать некоторым максимальным значением параметра целого – величиной . Отношение к периоду существования системы или структуры , характеризует некоторую среднюю скорость роста и последующего разрушения структуры.

Процессы такого бурного (или не очень бурного) роста могут сильно отличаться друг от друга, однако во многих случаях они обладают некоторыми общими особенностями.

    Эти особенности изменения параметра целого, в некоторой степени характеризующего степень зрелости системы, могут быть исследованы эмпирически и описаны математическими уравнениями.

 

 

5 Эмпирический анализ двумерного фазового пространства, описываемого выбранным параметром целого и скоростью его изменения или некоторым итерационным процессом.

 

    Если параметр целого выбран, то на основании эмпирических данных может быть построена для данной системы или для серии систем, аналогичных данной, зависимость параметра целого, характеризующего систему, от времени. Эта зависимость может быть дискретной, когда для некоторых выборочных промежутков времени осуществляется определение выбранного параметра, или непрерывной, в этом случае при помощи специальных приборов осуществляется непрерывная запись некоторых величин, которые затем могут быть при помощи математических выкладок преобразованы в выбранный параметр.

    Наиболее реалистичным является дискретное определение зависимости параметра от времени с последующей аппроксимацией полученных данных в виде непрерывных функций от времени.

    В этом случае вместо зависимости параметра от времени может быть построена более информативная картина двумерной фазовой плоскости, по оси абсцисс которой отложен выбранный параметр, а по оси ординат – его производная по времени.

    Для автономных систем, то есть систем, динамика развития которых слабо зависит или вовсе не зависит от параметров окружающей среды (поля), такой график может оказаться универсальным, не зависящим от начальной точки отсчёта во внешнем времени.

    Здесь проявляется искусство (а точнее интуиция) в выборе параметра целого - он должен быть выбран таким образом, чтобы характер его изменения был универсальным для всех квантов той обобщенной волны, которую они формируют. То есть, чтобы зависимость его изменения от времени для данной структуры была детерминирована и слабо зависела от внешних условий.

    Однако любая сложная система может считаться автономной лишь приближённо.

 

         3.Разработка одномерной математической модели динамики объекта в рамках выбранного нами параметра целого.

   

    Если определен один параметр, интегрально определяющий меру структуры, то можно построить простейшие математические модели, приближенно описывающие процесс формирования, роста  структуры и выхода её на тот или иной стабильный режим, а также процесс её разрушения или превращения в качественно новую структуру.

    Введём для параметра целого, описывающего структуру, обозначение .

Математика предлагает два типа аппроксимации - дискретный и непрерывный,  отличающиеся друг от друга и имеющие каждый свою сферу рационального применения.

Дискретный способ аппроксимации параметра целого состоит в выражении последующего измеренного состояния системы через предыдущие

 .

Особо следует выделить системы, которые, несмотря на их сложность, в процессе своего существования могут принимать, хотя и большое, но конечное число состояний.

Динамика таких систем оказывается во многом эквивалентной динамике орбит конечных математических полугрупп или групп, классификация которых близится в настоящее время к завершению.

 Наиболее известным  представителем таких систем является современный компьютер, который может быть использован для моделирования их динамики.

Практически неограниченное развитие компьютерной техники и сферы  её использования  свидетельствует о возможности широкой применимости дискретных моделей с большим, но конечным числом возможных состояний, то есть значений параметра целого, для достаточно подробного описания природных и техногенных систем и процессов .

Фазовое пространство при итерационном процессе может быть построено следующим образом. По оси абсцисс откладывается , а по оси ординат. Точка на соответствующей фазовой плоскости соответствует отображению. Для систем с конечным числом состояний количество точек конечно и равно числу состояний.

Любой динамический процесс такого типа в пределе выходит на стационарную  точку,

 

 или на циклическую траекторию.

 ,

где  можно считать периодом цикла.

В пределе очень большого числа состояний область изменения обобщённых координат системы и, следовательно, соответствующего изменения параметра целого может  быть аппроксимирована континуумом. И для моделирования динамики параметра целого могут быть использованы непрерывные функции, которые аппроксимируются, например, дробно-полиномиальными функциями.

    Этот способ приводит в случае автономных систем  к итерационному процессу вида

,

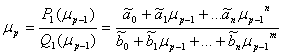 aнализ которого, особенно в комплексной области, к рассмотрению которого мы вернёмся, привел к удивительным открытиям в теории динамических структур и систем [11].

     В случае бесконечного числа состояний количество типов траекторий становится значительно больше, чем при дискретном задании.

Практический интерес представляют аппроксимирующие функции, гладкие  на всём промежутке изменения параметра целого, но имеющие разрывы функции и их производных в конечном числе точек. В этом случае особые точки отображений и аттракторы приобретают дополнительные специфические особенности/

        В случае непрерывной и гладкой зависимости параметра целого от времени мы можем для описания динамики его развития  записать дифференциальное уравнение  [4,9], где -гладкая функция, решение и качественный анализ которого при условии знания функции , позволяет не только приближенно описывать динамику структуры, но и в какой-то степени предсказывать её будущее. Если структура или система, в основном, развивается по собственным законам, (воздействие внешней среды (поля) на неё пренебрежимо мало либо носит стационарный характер), то для её описания может быть использовано автономное дифференциальное уравнение,

,

решение которого инвариантно относительно начала, а сама система в первом приближении может считаться автономной. Изменяя коэффициенты полиномиальной аппроксимации функции , можно аппроксимировать полиномами достаточно широкий класс зависимостей для различных типов структур [10]. Анализ влияния коэффициентов на решение уравнения, положение его стационарных точек и точек бифуркации представляет собой интересную и практически полезную математическую задачу, решение которой позволяет не только анализировать эмпирические данные, но и предсказывать с некоторой степенью достоверности вероятное будущее исследуемой системы.  

В случае непрерывной аппроксимации наиболее удачным подходом является  построение двумерных фазовых диаграмм, по одной из осей которых откладывается сам параметр, а по другой – его производная. Для автономных объектов, для которых фазовые диаграммы не включают в себя явной зависимости от времени, задача аппроксимации значительно упрощается.

В некоторых случаях  дифференциального уравнения первого порядка для адекватного описания динамики параметра целого оказывается недостаточно. В этом случае можно перейти к дифференциальным уравнениям более высоких порядков или к введению комплексного параметра целого. В обоих случаях этот переход эквивалентен увеличению числа переменных.

 

5. Качественный анализ одномерной математической модели динамики объекта.

 

Качественный анализ итерационной системы или нелинейного дифференциального уравнения позволяет ещё до  их решения определить особенности поведения моделируемой системы как нелинейного объекта не только в прошлом и настоящем, но и в будущем.

Начнём анализ с автономной итерационной системы.

Выполнение условия

                                                            

означает , что система находится в таком состоянии, что значение её параметра целого в каждый следующий после  момент времени переходит само в себя , т.е. не меняется. Таким образом, состояние системы, соответствующее , на данном уровне рассмотрения является стационарным.

Будем обозначать соответствующие значения параметра целого

                                           

Т.е. для всех  справедливо равенство

В нелинейных системах различают устойчивые и неустойчивые стационарные состояния. Стационарное состояние называется устойчивым и обозначается ,если существует некоторая достаточно большая область ( окрестность )  в фазовом пространстве такая, что, как только процесс в какой-то момент времени пришел в состояние из этой области , то он начинает стремиться и в пределе достигает устойчивого состояния неизменности параметра целого. Если такой области нет, т.е. если микроотклонение от точки, соответствующей стационарному значению, приводит к существенным макроизменениям в течении процесса , фатальной утрате этой стационарности, состояние системы является неустойчивым стационарным состоянием.

В общем случае график  ,  соответствующий азностному уравнению, иллюстрирует закон эволюции системы и позволяет определять стационарные состояния системы и их тип.

    Здесь необходимо сделать несколько принципиальных замечаний, связанных с неопределенностью и дополнительностью.

 

Вспомнив наши предыдущие рассуждения, мы можем  утверждать, что точно определить меру , характеризующую нашу структуру, мы не можем. И наряду с мерой, определяющей объём многообразия фазового пространства, описывающего структуру, естественным образом возникает вероятностная мера того, что исследемая величина единственной обобщенной координаты  принимает именно то значение, которое мы определяем. Тем самым сразу же возникает двойственность описания. Любое детерминированное описание, использующее дифференциальные уравнения либо отображения областей друг на друга должно сопровождаться дополнительным к нему вероятностным описанием, характеризующим меру и характер распределения отклонения реальной величины меры от расчетной.

 

Введение такой двойственности приводит к необходимости рассмотрения третьей величины, характеризующей структуру или ее модель - этой величиной может являться соотношение мер. Это соотношение может проявляться в виде какой-то функции этих величин. Элементы указанной триады могут, в зависимоcти от ситуации и метода рассмотрения меняться местами [30], [31].

    Возможен и другой подход, связанный с введением понятия энтропии и комплексификацией параметра целого, который изложен ниже.

     Если параметр целого, характеризующий структуру, выбран удачно и если динамика структуры определяется (в основном) её внутренними механизмами (структура, в основном, автономна) и эмпирически обнаружена гладкая зависимость параметра целого от времени, то в первом приближении динамика её развития на этапе возникновения и роста может быть описана автономным дифференциальным уравнением:

 

                           (1.6.2)

 

Подробный качественный анализ этого уравнения с введением фазового пространства и других понятий качественного анализа приведен в [29] .

 

Общее решение уравнения (1.6.2) имеет вид

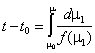                               (1.6.3)

 

Выражение (1.6.3) в неявной форме непосредственно связывает меру, характеризующую структуру, со временем. Оно может быть использовано в качестве базы для эмпирического исследования сложных структур, параметр целого которых определён достаточно корректно. Если для какой-либо  изучаемой нами структуры в определенные  моменты удалось экспериментально определить как величину выбранного нами параметра целого, так и его производной по времени, то затем, введя простейший тип аппроксимации функции , мы можем получить систему уравнений для коэффициентов аппроксимации и приближенно описать динамику изучаемой системы, например, при помощи дробно-рациональной функции.

              (1.6.4)

 

Варьируя коэффициенты , можно аппроксимировать достаточно широкий класс экспериментальных зависимостей для различных типов структур и систем.

Для дробно полиномиальных функций существует общий алгоритм нахождения интеграла движения. Анализ влияния коэффициентов  на решение уравнения (1.6.4) представляет собой интересную математическую задачу, которая в свете сказанного нами ранее может иметь важные практические приложения при первичном качественном анализе сложных структур и систем. Разлагая числитель и знаменатель правой части уравнения (1.6.4) на простейшие сомножители и выбирая из них те, которые соответствуют положительным действительным корням, определяем нули и полюса для производной. Рассматривая поведение дифференциального уравнения вблизи нулей и полюсов первого порядка, получим всего лишь два типа локальных линейных дифференциальных уравнений и соответствующих им решений.

    Большой интерес представляют катастрофические явления, связанные со сближением корней полиномов между собой. В этом случае, как это будет показано ниже , возникают режимы с обострением. (Заметим, что в случае комплексификации мы получим непрерывный аналог проблемы Г.Жюлиа  и П. Фату.[16] и число корней полинома окажется равным его степени; к анализу этого случая мы будем возвращаться неоднократно ).

     Одним из вариантов функции является линейная зависимость. Вблизи нуля первого порядка, соответствующего значению , к этому уравнению cводится общее уравнение (1.6.4)

 

                           (1.6.5)

 

Введя замену переменных  , получим уравнение ,

а, изменив масштаб времени , получим простейшее обыкновенное дифференциальное уравнение

 

 ,                              (1.6.6)

 

решение которого имеет вид:

 

,                           (1.6.7)

 

где  значение переменной  в момент времени . Полученное выражение, если его считать простейшей моделью поведения структуры вблизи точки начала её роста, дает достаточно богатую информацию о возможных закономерностях этого процесса в случае положительных значений.

    Первый и наиболее интересный вывод состоит в том, что непрерывным процессом, аналогичным тому, который описывается  уравнением (1.6.5), сам момент зарождения структуры описан быть не может .  -остаётся положительной величиной как при положительных, так и при отрицательных значениях времени .

 

    В связи этим рост новой структуры , описываемый уравнением (1.6.7 ), фактически является процессом потери устойчивости уже имевшейся структуры. Как показывает опыт изучения любых процессов быстрого роста новых структур: цепных химических реакций, роста паровых пузырьков при кипении, роста биологических многоклеточных объектов, роста популяций и т. д., в первом приближении именно экспоненциальным законом описывается процесс первичного увеличения той величины, которая является параметром целого изучаемой нами структуры.

    В этом случае, однако, непрерывность (и это происходит практически почти всегда) является лишь пределом реального дискретного процесса размножения или роста элементов структуры. Поэтому тот же процесс, который мы описываем непрерывно, может и, в принципе, должен быть описан дискретным образом.

    Рассмотрим эту возможность, следуя [16].  Пусть - начальная мера, описывающая структуру , - ее значение через  дискретных промежутков времени .

        Коэффициентом  прироста  называют  относительное изменение меры за один промежуток времени     .Если эта величина - константа, то закон, управляющий динамикой, имеет вид:

 

                       (1.6.8)

 

Через  промежутков времени мера. описывающая начальную фазу развития структуры будет равна

 

.                      (1.6.9)

 

Таким образом, получаем последовательность значений меры, характеризующей рост структуры в начальный период ее развития, которая представляет собой геометрическую прогрессию .

 

Этот же результат может быть получен и непосредственно из уравнения (1.6.6 ) путем его дискретизации.

 

.             (1.6.10)

 

Таким образом, даже в этом простейшем случае возможны принципиально два различных случая рассмотрения, которые в пределе при  для конечного времени  дают одинаковый результат.

 

Рассмотрим другой элементарный случай уравнения (1.6.4), соответствующий решению вблизи простого нуля знаменателя его правой части

 

.                           (1.6.11)

 

Скорость роста меры, определяющей структуру, обратно пропорциональна её величине. Решением уравнения (1.6.11) является следующее выражение для параметра целого

 

                           (1.6.12)

 

Решение (1.6.12) характеризует другой - бифуркационный способ формирования структур, который соответствует случаю роста структуры из конкретной точки бифуркации. Дискретным аналогом уравнения (1.6.12) является система отображений

 

                        (1.6.13)

 

Здесь интересной задачей является рассмотрение случая сближающихся корней числителя или знаменателя,

                   (1.6.14)

 

Структура, параметр целого которой описан этим уравнением, выходит на некотором расстоянии от особенностей на линейный рост, соответствующий постоянной и имеет очень близко от нуля и полюса соответствующие особенности а в промежутке ведет себя достаточно интересно, имея , по-видимому, несколько ветвей поведения. Я сталкивался .с такой функцией, решая задачу о движении суперкавитирующего  и глиссирующего крыла вблизи свободной поверхности воды , причем  роль  параметра играла глубина погружения.[32] .

 

Мы рассмотрели лишь простые нули и полюса дробно-линейной функции, стоящей в правой части уравнения (1.6.4).

Рассмотрим случаи нулей и полюсов - ного порядка, когда корни полиномов , входящих в (1.6.11) становятся равными . что, как легко видеть, приводит к режимам с обострением и к зависимости типа корня некоторой степени для бифуркационного случая зарождения структур.

 В частном случае имеем

 

                       (1.6.15)

 

Решение этого уравнения имеет вид

 

                         (1.6.16)

 

Если мы рассмотрим случай кратных нулей функции , то формула (1.6.16) примет вид

                       (1.6.17)

 

Положительное решение для - существует только при временах, предшествующих времени  . Тем самым, мы получаем серию степенных режимов с обострением в подвижной (зависящей от начальных условий), точке , после которых реальная структура параметр целого которой положительная величина, не может существовать. (- принимает отрицательные или комплексные значения ).         Тенденция к режимам с обострением встречается в широком классе природных явлений, в том числе и при исследовании роста человеческой популяции.

    Картина меняется на зеркальную, если в правой части уравнения (1.6.15) перед выражением стоит знак минус, что соответствует зеркальному отражению времени.

 При рассмотрении кратных полюсов функции  получаем . Чем выше степень полюса для тем круче кривая  вблизи полюса.

    Во многих случаях поведение системы вблизи нулей или полюсов описывается степенной функцией с рациональным или иррациональным показателем степени. В этом случае ещё в большей степени, чем выше проявляется скрытая от нас многозначность поведения исследуемой системы. Величины  могут принимать несколько  или бесконечное множество комплексных значений, физический смысл которых  для реальных систем требует специального выяснения.

        Экспериментальные данные показывают, что большинство структур после момента бурного роста выходят на некоторый стабильный режим, в котором структура находится значительное время, и благодаря наличию которого мы можем выделить её из окружающего мира. Зададимся вопросом, а нельзя ли в рамках уравнения (1.6.1 ) в первом приближении описать этот процесс?

Оказывается, это возможно путем рассмотрения всего лишь квадратичной функции .

 

Рассмотрим так называемое логистическое уравнение, которое было подробно изучено в связи с анализом роста и стабилизации популяций животных, однако имеет широчайшее применение при исследовании различных систем, так как приближённо отражает переход системы из одного стационарного состояния в другое. Если предположить, что в  уравнении (1.6.6) коэффициент при  с увеличением  уменьшается по линейному закону, то путем изменения масштаба  можно получить уравнение (черточки над  опускаем)  [29]

 

                            (1.6.18)

 

Проанализируем это уравнение более подробно, заодно введя ряд новых для нас понятий, широко используемых в теории динамических систем, которые были взяты на вооружение синергетикой. Исследуемый этим уравнением процесс имеет две стационарные точки 0 и 1. Вспомним наш первый подход к анализу структур. Точка 0 неустойчива - это значит, что новые структуры могут появляться, в частности, при неустойчивости старых. Точка 1 устойчива независимо от того, с какой стороны мы к ней подходим. Интегральные кривые уравнения (1.6.15) называются логистическими кривыми и имеют две асимптоты, к которым они стремятся в течение бесконечного времени.

 

Фазовая диаграмма уравнения (1.6.18) - зависимость от ,  представляющая собой параболу, наиболее сжато и полно характеризует особенности процесса .

 

В каком-то смысле логистическое уравнение универсально, так как его интегральные кривые описывают процесс перехода динамической системы с одного неустойчивого состояния в другое - устойчивое. В нашем частном случае оно характеризует типичный процесс роста и стабилизации структур различной природы.

 

Ввиду важности этого уравнения приведём его общее решение в случае

 

                        (1.6.19)

 

При малых  в момент начала роста структуры логистическая кривая асимптотически приближается к экспоненциальной. Однако, по мере увеличения меры  возникают процессы, препятствующие дальнейшему экспоненциальному росту структуры, и вблизи  = 0.5 начинается расхождение кривых, при этом логистическая кривая выходит на асимптоту =1, а экспоненциальная кривая уходит вверх.

Этот закон является простейшим законом, описывающим непрерывным образом формирование новых структур. Ввиду его широкой применимости остановимся на его интерпретации более подробно. Хотя в неживой природе мы достаточно часто встречаемся с формированием новых структур, однако наиболее широкий спектр явлений такого рода мы видим при анализе биологических или социологических явлений. В первом приближении рост любого многоклеточного организма, начинаясь с одной клетки, первоначально происходит по закону, близкому к экспоненциальному , а затем в силу тех или иных причин скорость роста замедляется и структура выходит на стационарное состояние. Причины замедления скорости роста могут быть самыми  разнообразными: нехватка пищи, появление ядовитых отходов обмена веществ, влияние электромагнитных и гравитационных сил , внутренняя самоорганизация структуры.

 

Во многих случаях процесс роста сложных структур происходит не непрерывно, а путём скачкообразных процессов размножения элементов структуры или поглощения растущей структурой новых элементов. Если скачки меры, определяющей структуру, малы, то в первом приближении этот дискретный процесс может быть заменён непрерывным и вновь для его описания может быть использован механизм дифференциальных уравнений, в противном случае для описания динамики роста и стабилизации структур может быть использован аппарат конечно-разностных уравнений, как это было сделано ранее .

 

Попытаемся получить такое уравнение как дискретную аппроксимацию обыкновенного дифференциального уравнения (1.6.18).[17]. . Представим производную в соответствии с её определением как предел разностного отношения.

 

.                          (1.6.20)

 

Тогда вместо дифференциального уравнения можно получить цепочку отображений последовательных состояний системы друг на друга в виде

 

                         (1.6.21

 

В последнем уравнении прямая зависимость от времени исчезла. Время присутствует здесь лишь через направленную  цепочку отображений. В случае  эта группа отображений преобразуется в непрерывную группу отображений, все элементы которой отображают решения уравнения (1.6.18) друг на друга. Если же параметр  принимает некоторое конечное значение, то система отображений (1.6.21), вообще говоря, становится существенно отличной от уравнения (1.6.18) и её свойства, необходимо изучать самостоятельно. При этом она соответствует некоторому иному дискретному механизму развития сложных структур, который также имеет место в действительности, например, если изменения меры, определяющей рост структуры происходит дискретным образом и мера этих дискретных изменений соизмерима с мерой, описывающей саму структуру. Проследим, следуя [17], что даёт рассмотрение уравнения (1.6.21 ), если оно получено из логистического дифференциального уравнения.

Имеем

 

 ,                    (1.6.22)

 

где .. Это уравнение было исследовано Фернхюльстом [17]. Появившееся при таком рассмотрении число  называется параметром роста. Так же, как и в уравнении (1.6.18), для имеются два значения, при которых значение меры, определяющей структуру, (например численность популяции или масса многоклеточного организма) не изменяется . Когда  структура полностью отсутствует и в этом случае без акта творения никакой рост невозможен ( что такое акт творения- это особый разговор). Однако если начальное значение меры  хоть немного отлично от нуля, то при   на следующем шаге итерации  мера возрастает   

Последовательные  значения  растут до тех пор, пока они не достигнут 1.  При этом, в отличие от непрерывного рассмотрения, при некоторых значениях  достижение 1 возможно за конечный промежуток времени. Конечность приращений позволяет точно выходить на асимптоту. Однако, если в случае непрерывного рассмотрения стационарное состояние, соответствующее стабильной структуре, было устойчивым, то в случае дискретного рассмотрения и соответствующего ему в природе случаю дискретного формирования структур, устойчивость состояния, ранее называвшегося нами стабильным, требует специального исследования, выполнявшегося рядом авторов и приведшего к многочисленным открытиям, легшим в основание принципиально новых методов исследования сложных структур и систем.

 

Конечно-разностным аналогом более общего уравнения (1.6.4) является уравнение

 

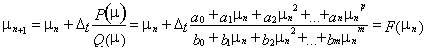   (1.6.23)

 

В случае комплексификации неизвестной функции мы приходим к анализу множеств Жюлиа и Фату, а также выходим на понятия фрактальной геометрии, цепочки бифуркаций, аттракторов странных аттракторов, числа Фейгенбаума и многих - многих других интересных вещей .за рассмотрением которых отсылаем читателей к монографии [17].  Здесь лишь отметим, что уравнение (1.6.4) и его дискретный аналог (1.6.23) содержат  бифуркационных параметров и к анализу их правой части могут быть привлечены все методы теории катастроф, а следовательно построена и классификация бифуркаций стационарных точек и полюсов этих уравнений.

    Устойчивые стационарные точки фазовой диаграммы или графика, представляющего решение системы итерационных соотношений являются пределом, к которому стремятся фазовые траектории системы. Такие точки называются аттракторами.

    Аттракторами могут быть не только устойчивые стационарные точки, но и замкнутые траектории циклического типа (циклы). В последние годы открыты и в настоящее время интенсивно изучаются ациклические аттракторы, названные странными. Более подробный качественный анализ особенностей динамических систем  должен  выполняться  на следующих этапах исследования.

       Особенно интересно классифицировать аттракторы и репеллеры итерационных процессов и дифференциальных уравнений, в которых аппроксимационные функции имеют разрывы. В этом случае появляются новые неожиданные варианты поведения исследуемой системы. Одной из таких особенностей является размножение скачков при многократном использовании итераций и даже стремление числа скачков к бесконечности. Одновременно появляются  не

отдельные аттракторы, а группы близких аттракторов, условия выхода на которые определяются выбором начальных условий при изучении системы.

 

 

5. Численное  решение полученных уравнений или цепочек отображений  и получение теоретических результатов, позволяющих осуществлять прогноз будущего развития системы.

 

Следующим этапом исследования является численное  решение полученных уравнений .

Численное  решение позволяет строить не только известную уже зависимость меры от времени, которая была в прошлом, и сопоставить полученные данные с результатами наблюдений и материалами качественного анализа, но и предсказывать характер этой зависимости, которого следует ожидать в будущем.

                                                    

 

                             

 

 

 

 

 

                                                            Этюд 3

 

Комплексный параметр целого. Обзор выполненных исследований.

 

Математическое моделирование самоорганизующихся структур и систем начато с простейшего случая, который легко реализуется  на компьютере.

     Введено понятие автономной динамической структуры с конечным числом возможных состояний. 

Переход из одного момента времени в другой характеризуется некоторым  многозначным отображением одного состояния в другие. В рамках этого отображения переход из одного возможного состояния в другое, определяемый функцией, осуществляющей это отображение, характеризуется некоторым числом, которое будем называть вероятностью перехода. Тогда, если каждому моменту внутреннего времени сопоставить некоторое распределение вероятностей возможных состояний, то соответствующее распределение вероятностей состояний системы можно определить в любой другой момент времени как в прошлом, так и в будущем. Такая бифуркационная система названа автономной. Для этой системы, в случае конечного числа возможных состояний, может быть построен наложенный на собственное время граф бифуркационных событий с соответствующими этим событиям относительными вероятностями. Тем самым, вводится автономный вектор вероятности состояний, изменяющийся по наперед заданному закону, определяемому не зависящей от местного времени матрицей перехода.

Изучение свойств таких систем эквивалентно изучению свойств одного из частных случаев марковских процессов [9].

Рассмотрены частные случаи автономных бифуркационных систем с конечным числом возможных состояний и осуществлена их классификация.

Изучение динамики модели бифуркационной системы с конечным числом возможных состояний позволяет предложить её в качестве основного элемента нового типа компьютера, который мы назвали целостным.

Такой компьютер должен включать в себя триаду элементов, являющихся, как это было показано нами в [6], необходимыми составляющими любой самоорганизующейся транспортно-информационной системы.

 

Поле

/        \

                                   Собственно структура  ----- Контроллер

 

Целостный компьютер должен иметь квазифрактальную структуру - целостными должны быть не только компьютер, но и его элементы, а также иерархия его подсистем и систем, которые формируются из компьютеров этого типа.

Собственно структурой целостного элемента такого компьютера может стать бифуркационный элемент - компьютерная реализация динамики автономной бифуркационной системы с двумя возможными состояниями.

Контроллером элемента целостного компьютера является внутренний механизм, вырабатывающий значение величины распределения вероятности между двумя состояниями элемента.

Кроме того, должен существовать генератор действительных чисел, который может моделировать поле элемента.

Перечислим некоторые из задач, которые могут быть решены при помощи целостного компьютера.

1.    Математическое моделирование стохастических процессов, в частности, марковских цепей.

2.    Описание цепочки бифуркационных событий, при реализации каждого из которых компьютер может с определенной вероятностью выйти на некоторый детерминированный алгоритм, завершающийся очередным бифуркационным событием. Тем самым возникает возможность создания компьютерной модели бифуркационного процесса.

3.    Моделирование некоторых аспектов самоорганизации сложных динамических систем (например, режимов самоорганизованной критичности).

4.    Изучение динамики размножающихся систем и процессов.

5. Анализ генезиса устойчивых статистических распределений  в транспортно-информационных системах, а также моделирование явления эволюции реальных структур и систем.

Если ввести в рассмотрение внешнее время как непрерывно изменяющийся параметр, то всякая автономная структура, несмотря на потенциальную бесконечность, имеет начало и конец, а следовательно, какой-то период существования и тем самым отличается от рассмотренной выше идеальной модели, имеющей потенциально бесконечное время существования.

Простейший, наиболее схематический вид описания этого свойства реальных структур  состоит в представлении динамики структуры в виде двух чисел 0 и 1,  где 0 соответствует отсутствию структуры, а 1 - ее существованию. До момента  структуры не существовало. Мера  существования  заданной структуры, равнялась нулю. В момент  произошло рождение структуры, которая просуществовала до момента времени , после которого она исчезла. Даже такое простейшее рассмотрение позволяет ввести ряд понятий.

 

1. Момент рождения структуры .

2. Момент разрушения - исчезновения структуры .

3. Срок жизни структуры  .

 

Если процесс существования структур рассматривать как непрерывный во времени, то в моменты возникновения и разрушения структур в природе должны происходить качественные изменения (ведь рождается (или исчезает) нечто существенное). При простейшем рассмотрении можно считать, что рождение и исчезновение структуры происходят мгновенно. Это достаточно сильное допущение, хотя во многих случаях действительно происходит очень быстрое формирование новых структур и разрушение старых. Не зря в человеческом языке существуют такие слова, как катастрофа, кризис, взрыв, революция и т.д. Однако, как бы быстро ни происходило в некоторых случаях формирование новых структур, всё равно это процесс, имеющий ту или иную протяжённость во времени. В некоторых случаях процесс формирования структур может оказаться достаточно длительным. Какие же изменения в рассмотренном нами подходе можно ввести, если учесть указанные обстоятельства? Вместо мгновенного формирования структуры и мгновенного её разрушения необходимо ввести какие-то конечные периоды возникновения и разрушения структуры. Это вполне естественное допущение влечёт за собой ряд следствий.

Первое следствие состоит в том, что возникает вопрос, а что же происходит со структурой в эти периоды? Существует она или нет? Ответ на этот вопрос совсем не тривиален. По-видимому, в периоды рождения и разрушения про структуру нельзя с полной определённостью сказать ни то, что она существует, ни то, что её нет. Если всё же считать процесс формирования структуры непрерывным и в момент структура отсутствует- 0, а в момент  структура существует-1, то точки траектории структуры на временном отрезке , можно соединить плавной кривой. Значения величин функции, описываемой этой кривой, можно интерпретировать как меру существования (зрелости) структуры. В период рождения нельзя сказать, что структура не существует, но ещё нельзя сказать что структура уже полностью оформлена.

 Попытаемся решить эту задачу с другой стороны. Мера, характеризующая произвольную структуру, может быть получена, например, как объём многообразия, определяемого обобщёнными координатами внутреннего пространства. Этот объём может меняться в процессе существования структуры. Если структуры нет, то нет и многообразия, ее описывающего. В процессе существования (функционирования) структуры существует какой-то промежуток времени, когда многообразие, описывающее структуру, имеет максимальный объём. Если объём многообразия, описывающего структуру в любой момент времени, поделить на его максимальное значение, то получим в наиболее естественном случае некоторую кривую зависимости этой относительной величины от времени, начинающуюся с нуля и плавно выходящую на единицу.

     Рассмотрим некоторые общие закономерности, связанные с этапом рождения структуры. Как следует из той информации, которую мы получаем при изучении природы, можно рассматривать несколько способов рождения новых структур.

а) Появление новой структуры (волны) вследствие объединения или самоорганизации нескольких однородных структур (квантов).

б) Появление новой структуры в результате деления структуры на две и более частей.

в) Появление новой структуры или нескольких новых структур вследствие потери устойчивости структуры, существовавшей до их образования

г) Рождение новой структуры в результате полного или частичного слияния двух родственных структур с возможным переходом затем к многократному использованию  второго способа.

д) Рождение новой структуры путем излучения структур более высоких классов.

е) В качестве отдельного способа может рассматриваться целенаправленное формирование новых структур структурами более высокого класса.

Способы рождение новых структур в биологии описаны, например, П. Тейьяром де Шарденом.[10,с. 90].

Большинство описанных способов  приводит к необходимости анализа процесса формирования новых структур как бифуркационного изменения старых, уже существовавших ранее систем и структур . Тем самым, процесс появления и разрушения структур включается в цепочку превращений одних структур в другие [6].

Во многих случаях мы считаем, что структуры после своего появления начинают изменять значения обобщённых координат, не меняя, например, числа обобщённых координат приближенно описывающего их многообразия.  В качестве примеров можно привести:

а) рост амплитуды поверхностной морской волны при приближении её к берегу;

б) рост парового пузырька или паровой каверны при увеличении скорости движения тела;

в) рост кристаллов в растворе;

г) рост атомного гриба;

д) рост живого организма;

е) рост числа научных исследований в новой отрасли знаний.

Процессы такого роста могут значительно отличаться друг от друга, однако во многих случаях они обладают некоторыми общими особенностями. Если для структур такого типа может быть введён какой-либо один параметр, интегрально определяющий меру структуры (параметр цeлого), то в некоторых случаях можно не только выделить общий механизм формирования таких структур, но и найти простейшие математические модели, которые приближенно описывают этот механизм и которые позволяют моделировать количественные и качественные закономерности роста структур в данном случае.

В [6] показано, что при анализе динамических структур и систем можно ввести комплексную волновую функцию (вектор-матрицу), описывающую динамическую систему (структуру), реальная и мнимая части которой связаны с мерой, характеризующей её внутреннее фазовое пространство и вероятностными характеристиками бифуркационных событий, в которых структура участвует.

     Эти обстоятельства позволяют рассматривать в качестве математической основы для  исследования структур на первом этапе цепочку голоморфных функций комплексной переменной [11]. Эта переменная может быть названа комплексным параметром целого структуры (или комплексным параметром Планка).

В соответствии с высказанной гипотезой на следующем шаге рассмотрения в качестве области определения комплексной меры, описывающей возможные совокупности состояний, в которых может находиться динамическая система, принято поле комплексных чисел (поле действительных чисел рассматривается как частный случай этой более общей области рассмотрения ).

Подробно исследована цепочка линейных отображений комплексного переменного, и изучены характерные особенности этой динамической системы. Показано, что при определённых условиях в пределе большой частоты итераций динамика такой системы становится эквивалентной динамике, описываемой комплексным линейным дифференциальным уравнением. Получено общее решение этого уравнения в виде экспоненциальной функции от времени. Возможна такая интерпретация природных явлений, что обычное внешнее время - время взаимодействия  является лишь линейным приближением к реальному (экспоненциальному) времени динамической структуры (касательной к экспоненциальной кривой в единице). Тогда реальным временем, определяющим динамику структуры, может явиться не линейное время, а экспоненциальное время. В этом случае главную роль в анализе динамики структур играют не экспоненциальные, а степенные функции. Вполне возможно, что это частично объясняет вездесущность степенных функций при изучении самоорганизующихся структур.

Аналогичный подход к волновой функции позволяет ввести в рассмотрение экспоненты от степенных функций, общие свойства которых и возможные области их применения в настоящее время ещё мало изучены.

Замена параметров времени и волновой функции позволила осуществить цепочку трансформаций линейной системы [12]. В данном частном случае проявилось основное структурное свойство математических моделей (а следовательно, и структуры природных объектов, которые они описывают). Если применить к математическим исследованиям основную триаду Р.Г.Баранцева [13-18 ]

 

                                                    Интуицио

                                               /               \

                                        Рацио -------- Эмоцио,

 

то она может быть отображена на некоторое трёхмерное абстрактное пространство, обобщёнными координатами которого являются

                                          

 

                                       Континуальность

                                             (Мощность)

                                          /                           \

                             Размерность ---------- Иерархия

                     (Число переменных)    (Степень нелинейности)

 

Рассмотрим первоначально движение по оси континуальности.

     В начале этой оси можно расположить числа 0 и 1, связь которых с реальными объектами была установлена нами ранее. Следующими на этой шкале располагаются конечные множества (которые могут быть взаимно однозначно отображены на конечную совокупность целых чисел). Далее на шкале континуальности расположены счетные бесконечные множества (натуральный ряд чисел, бесконечные последовательности, совокупность рациональных чисел и т. д.). Ещё далее множества, обладающие мощностью континуума (иррациональные числа, действительные числа, комплексные числа, конечномерные матрицы и т.д.). Дальнейшее продолжение шкалы лежит в области определения мощности совокупности подмножеств множества мощности континуума [19]. 

Аналогичным образом можно перемещаться по оси размерности. Размерность – понятие, характеризующее число одновременно рассматриваемых переменных. Величина размерности может пробегать ту же совокупность значений, что и величина континуальности – от нуля и единицы до континуального множества координат, и, возможно, далее .

Анализ иерархической координаты математики начнем с линейных отображений. Линейная функция может быть определена на любой точке плоскости, формируемой двумя первыми координатами: мощностью и размерностью. Однако, уже анализ цепочек линейных отображений, подобный кратко описанному нами ранее для множества комплексных чисел выводит на следующий уровень иерархии. Цепочка линейных отображений, определяемых заданной функцией, порождает некоторый процесс, являющийся моделью потенциально бесконечной структуры. Эта последовательность порождает новый, сначала дискретный (принимающий последовательно целые значения) параметр времени, который при помощи предположения о гладкости рассматриваемых функций может быть преобразован в континуальный параметр. На этом уровне в математике появляются системы линейных дифференциальных уравнений, решениями которых оказываются экспоненциальные отображения. Этот процесс, с теми или иными особенностями, происходит над всей плоскостью континуальность - размерность и именно его изучению посвящена большая часть математических исследований.

Второй этаж иерархии формируется из первого путем взятия обобщенных экспонент от линейных операторов, действующих на первом этаже. Аналогично, переход от второго этажа к первому можно рассматривать как обобщённое логарифмирование функций и операторов, действующих на втором этаже.

Операции, выполненные нами при выводе степенных дифференциальных уравнений первого порядка, указывают на возможность рассмотрения связи между собой функций, находящихся на втором уровне иерархии. Эта связь - степенная. В этом случае мы оказываемся в области математики, которая названа А. Д. Брюно [20] степенной геометрией, включающей в себя в качестве частных случаев ряд интенсивно развивающихся в настоящее время разделов современной математики. Изучение конечных сумм и интегралов по показателям степени от степенных мономов одной или многих действительных и комплексных переменных представляет собой проблему, далеко не исчерпанную современной математикой (смотри, например, [11], [20], [21], [22], [23], [24], [4], [25], [26], [27], [28], [29], [31]). Уже на этом уровне, особенно при анализе функций с комплексными показателями степени, появляются многозначные (и даже бесконечнозначные ) отображения, лежащие пока ещё вне основной магистрали математических исследований.

Особую роль в классических исследованиях играют полиномиальные функции, которые, являясь частным случаем степенных полиномов, аппроксимируют гладкие многообразия. Именно в анализе полиномиальных функций нескольких переменных лежат основы теории особенностей гладких отображений и теории  катастроф [21], [25-29].

Однако, произвольные степенные функции и соответствующие им дифференциальные уравнения начали изучаться сравнительно недавно [20], хотя  многочисленные примеры исследования динамики нелинейных процессов, происходящих в самоорганизующихся структурах и транспортно-информационных системах свидетельствуют о том, что степенные функции встречаются повсеместно [20], [31], [32], [33], [77].

В связи с развитием голоморфной динамики [11], теории множеств Жюлиа и Фату [25], фрактальной геометрии [27] начались интенсивные исследования в области перехода со второго этажа на третий, где многозначность функций, графы, дробная размерность, вероятность реализации того или иного значения функции оказываются наиболее существенными особенностями исследуемых объектов. Вся интенсивно развивающаяся теория случайных процессов также относится к третьему уровню иерархии. Именно на третьем уровне иерархии исследователей ждут неожиданности и открытия.

При исследовании динамики комплексного параметра целого нами введена одна из возможных модификаций комплексных чисел, использование которой позволяет, если это необходимо, рассматривать степенные функции комплексного переменного с комплексными показателями степени как однозначные функции, а следовательно, применить к их исследованию аппарат функционального анализа [32].

Выполненные исследования позволили, в частном случае, построить цепочку связанных между собой комплексных математических моделей динамики размножения и роста живых субъектов, начиная от изолированной клетки и кончая популяцией организмов, в частности, человеческой популяцией, подробности построения которой изложены в четвёртой главе второй части настоящей монографии. Сделана первая попытка идентификации реальной и мнимой частей комплексного параметра целого [6 ] человеческой популяции как целостной системы.

 

 

 

 

 

.

Этюд 4

Развитие структур. Динамика Ферхюльста.

 

Окружающий нас мир состоит из структур (материальных объектов).

Обычно каждая структура в процессе своего существования проходит четыре периода:

Рождение.

Развитие.

Стабильное существование.

Разрушение.

При этом в частных случаях возможно как увеличение, так и уменьшение числа периодов.

Каждый период обладает своими особенностями, общим для различных структур.

Развитие структур.

Многие структуры после своего появления начинают значительно изменять свою форму и размеры, не меняя существенных признаков, определяющих структуру как таковую. В качестве примеров можно привести:

А Рост пузырька газа в жидкости.

Б. Рост капли перед падением с крыши.

В. Рост живого организма.

Г. Рост кристаллов в растворе.

Д. Рост числа людей в человеческой популяции.

Е. Рост числа хост-компьютеров в Internet.

Е. Рост числа научных исследований.

Сформировавшаяся структура может после момента своего рождения в течение некоторого времени находиться в неравновесных состояниях, с количественным, но не качественным изменением своих параметров.

Эти процессы имеют ряд общих свойств, для описания которых могут быть использованы универсальные математические методы.

В начальном периоде роста в большом количестве случаев действует некоторый закон изменения главного параметра, описывающего систему (параметра целого), представляемый дифференциальным уравнением

,

Другой формой математической записи процесса роста является итерационный процесс 

Предположим, что

Или

 

Если предположить, что

то получаем следующее итерационное соотношение Фернхюльста [1]

Так же как и в случае логистического уравнения, параметр целого  имеет два значения, при которых возникает стабилизация.

 

Если начальное значение  принять равным нулю, то есть структуры нет, тогда рост невозможен и уравнение отражает этот факт. Однако, если начальное значение  параметра целого хотя бы немного больше нуля то на следуюшем шаге итерации это значение возрастёт. Следовательно, это состояне равновесия является неустойчивым.

Последовательные значения  растут, пока они не достигнут 1.

Для того, чтобы определить характер устойчивости состояния равновесия, проследим, как изменяются во времени малые отклонения .

Подставляя это соотношение в разностное уравнение, получим конечно-разностное уравнение для

 

Отсюда следует, что по абсолютной величине меньше, чем , когда .

Следовательно, такой переход конечно-разностному уравнению не порождает эквивалентности- При  итерационная система сводится к логистическому дифференциальному уравнению, имеющему аналитическое решение. Введение дискретности придаёт системе новый параметр . Чем больше , тем больше дискретная система отличается от непрерывной. В природе такая дискретность реализуется повсеместно. Например, рождение нового организма  происходит через некоторое дискретное значение времени. Изменение параметра целого происходит скачкообразно. Параметр скачкообразности . Этот же параметр может считаться параметром квантования. Если параметр квантования меньше единицы, то с увеличением устойчивость системы первоначально увеличивается

.

Если , то

.

При этом если

 

При очень малых  стремление к нулю осуществляется с колебаниями около нуля. Амплитуда колебаний тем меньше, чем меньше .

 Если  отрицательно, то стремление осуществляется без колебаний.

Наиболее быстрое стремление к стационарной точке  происходит при=0.

Возможно, что этот процесс частично объясняет гипотезу В. М. Дильмана о чувствительности гипоталамуса, которая определяет старение.

При  точка  становится неустойчивой. Процесс начинает периодически осциллировать между двумя уровнями. Это наводит на мысль о рассмотрении  первую итерацию соотношения Ферхюльста

 Тем самым мы переходим к бифуркации рождения цикла

Дальнейшие рассуждения приведут нас к числм Фейгенбаума и странным аттракторам.

Здесь возникает интересная проблема, связанная с эквивалентностью дифференциальных уравнений и конечно разностных соотношений. Вместо производной мы вводим приращение и получаем некоторый сдвиг по фазе. Приращение происходит в точке, отстоящей от точки, в которой вычисляется правая часть уравнения. Это напоминает уравнение с запаздыванием. И действительно, те явления неустойчивости, которые были описаны выше и которые приводят к бифуркации рождения цикла и к другим более сильным бифуркацям, а затем и к хаосу, могут быть поучены также аналитическим методом, а менно путём рассмотрения уравнения с запаздыванием.

Б. Хассард , Н. Казаринов, И. Вэн Теория и приложения бифуркации рождения цикла

Глава 4 Приложения. Дифференциально- разностные уравнения.

П. 3. Уравнение Хатчисона – Райта и связанные с ним задачи.

Природные популяции не могут мгновенно реагировать на внешние воздействия – реакции наступают через некоторый промежуток времени. Например, даже в идеальных климатических условиях рождаемость скота будет зависеть (из-за оскудения пастбищ, не только от численности стада, но его численности в прошлом на интервале времени, приближённо равном периоду восстановления пастбища. Запаздывание может быть также обусловлено длительным достижением репродуктивного возраста, как это происходит у лососевых. И репродукционные , и другие запаздывания могут существовать одновременно. Одна из первых математических моделей в биологии, учитывающая временные запаздывания, была предложена Хатчисоном.

Hutchison G.E. Circular causal systems in ecology Ann. N.Y. Acad. Sci. 1948.50. pp 221-246.

Он рассматривал популяцию, подчиняющуюся модифицированному логистическому закону роста. Именно, сомножитель , учитывающий наличие верхней границы численности популяции, вычисляется в некоторый  предшествующий данному момент времени.

Здесь   - максимально возможная стационарная численность популяции. Если под  понимать численность стада, пасущегося на лугу с временем восстановления растительного покрова , то из последнего уравнения будет следовать, что достижение численности   приводит к отсутствию её роста в момент времени.

(Если  , что можно получить, обезразмерив  по .)

Далее введя новый параметр

 Получим модифицированное безразмерное логистическое уравнение.

Таким образом, уравнение Хатчисона превращается в модифицированное логистическое уравнение

Если затем ввести вместо другую величину, то мы получим конечно-разностное уравнение

 

Разрешая  это уравнение относительно

Введём обозначения

 

 

Пренебрегая квадратичными членами, получаем старое итерационное соотношение

Тем самым, мы показали, что запаздывание вблизи стабильного состояния эквивалентно квантованию логистического уравнения.

 

При  , то есть в момент рождения структуры, значение основного параметра  равняется . Затем это значение начинает расти по экспоненте и этот рост кажется на первых порах неограниченным.

Начальный период роста может характеризоваться и другими законами, например степенными, которые мы рассмотрим в отдельном этюде.

Однако экспоненциальный рост происходит лишь на первой стадии развития.

В действительности, в дифференциальном уравнении всегда присутствует квадратичный член,

,

 который при отрицательном значении  порождает стабилизацию структуры.

Выбрав соответствующие масштабы   и

Получаем  логистическое уравнение

Логистическое уравнение имеет общее решение в виде

.

При малых значениях  логистическая кривая практически не отличается от экспоненциальной, то есть ограничения, описываемые квадратичным членом, слабо влияют на рост структуры. Однако, по мере увеличения  рост перестаёт быть экспоненциальным и вблизи  происходит резкое разделение экспоненциальной и логистической кривых. Экспоненциальная кривая уходит вверх, стремясь к бесконечности, а логистическая- выходит на асимптоту, горизонтальную прямую , то  есть на стационарный режим.

 «До середины ХХ века наука росла экспоненциально. Если такой рост будет продолжаться, то к ХХI веку всё население Земли будет заниматься наукой, а для печатания научных статей не хватит всех лесов планеты.Следвательно, раньше должно наступить насыщение: мы находимся вблизи того места, где логистическая кривая начинает отставать от экспоненциальной. Например, число математических статей в научных журналах после Второй мировой войны до 70-х годов увеличивалось каждый год на 7%, а последние несколько лет – медленнее.» -писал в 1984 году В.И. Арнольд

 

аАрнольд В. И. Обыкновенные дифференциальные уравнения М.: Наука. 1984.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Совместное рассмотрение различных видов пространственных и временных резонансных явлений в рамках синергетики может привести к дальнейшему прогрессу в понимании закономерностей организации объектов живой и неживой природы».

А. Ю. Сунгуров [1].

 

«Изучая процессы самоорганизации в творческом акте переживания, человек вовлекается в соответствующее движение мысли и тем самым развивается сам. В целостном общении возникает синдром Пигмалиона.  Создавая Галатею синергетики, мы попадаем под её обаяние, способствующее сотрудничеству, сочувствию, соединению».

Р. Г. Баранцев [2].

                         

«… при определённой амплитуде инноваций существует опасность, что резонирующая инновация станет причиной деградации системы»

Н. В. Басов [3]

 

Этюд 5

Резонансы в конечномерных динамических системах.

 

1.                                                                                                                                                                                                             Классические определения резонанса.

 

    Важным элементом синергетической методологии изучения того или иного объекта является лингвистический анализ слова, которым он обозначен, и поиск определений, даваемых этому объекту различными авторами [4].

Ниже приведены некоторые определения понятия «резонанс», почерпнутые из Internet:

«Яndex.

1.Словарь по естественным наукам.

«РЕЗОНАНС - резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающего воздействия к некоторой фиксированной частоте (резонансной частоте). При наличии трения резонансная частота меньше частоты собственных колебаний системы» 

«Колебания»

Материалы представлены проектом Глоссарий –ru

http://slovari.yandex.ru/art.xml?art=gl_natural/2574/257_4912HTM&encpag...

2. Малый энциклопедический словарь Брокгауза и Эфрона.

«РЕЗОНАНС - физ., усиление звука вследствие передачи звуковых колебаний другим телам, способным издавать звуки той же высоты и потому становящимся звуковыми источниками.»

Материалы предоставлены компанией Новый Диск . Издание 1890-1907г.г. http://slovari.yandex.ru/art.xml?art=brokminor/34/34074HTM&encpage=brok...

3. Толковый словарь живого великорусского языка Владимира Даля.

«РЕЗОНАНС м. франц. зык, гул, рай, отзвук, отгул, гул, отдача, наголосок; звучность голоса, по местности, по размерам комнаты; звучность, звонкость музыкального орудия, по устройству его. || В рояле, фортепьяно, гуслях: дек, палуба, стар. палочка, доска, по которой натянуты струны.

Материалы предоставлены проектом Рубрикон

Даль В.И. издание 1863-66

©2001 Russ Portal Company Ltd.

http://slovari.yandex.ru/art.xml?art=dal/dal/03151/40800.htm&encpage=dal&...

 

 

 

2. Первичный лингвистический анализ слова «резонанс».

 

    Первые попытки перевести это слово на другие европейские языки привели к следующему результату: 

 Резонанс – английский – resonance, echo, response.

 Резонанс – немецкий – Resonanz, Wiederhall, Echo, Nachklang;

иметь резонанс –Resonanz finden.

 Резонанс – испанский- resonancia, repercusion;

иметь большой резонанс – tener gran resonancia.

 Резонанс – итальянский - risonanza, ripercussione;

иметь большой резонанс – avere una vasta risonanza.

Обратные переводы на русский язык.

Английский – resonant – русский а) звучащий, раздающийся, звучный;

                                                         б) плавный, назальный;

                                                         в) резонирующий, с хорошим резонансом.

Англ. echo – русский-I-существ. 1.эхо, отголосок, подражание.

                                                         Syn – imitation

                                                        2. подражатель, плагиатор (амер.)

                                      II  глагол   1.отдаваться эхом, отражаться.

                                                         2. вторить, подражать, поддакивать

                                                          Syn. –repeat, imitate.

    Эта работа может быть продолжена практически неограниченно. И  её результатом должно стать поле слов, связанных по смыслу и звучанию с изучаемым нами словом «Резонанс» и явлением, ему соответствующим.

Предоставляем читателю возможность выполнить её самостоятельно.

 

3. Исследование частоты встречи слова резонанс в Internet.

 

    Одним из элементов  методологии синергетического исследования  всё чаще становится оценка частоты встречи того или иного слова в Internet

    Internet ворвалась в нашу жизнь как захватчик (внешнее резонансное воздействие). Предоставляя, казалось бы, неограниченные возможности для получения необходимой человеку информации, Сеть одновременно поглощает поверившего ей и часто, наоборот, не позволяет получать необходимые знания, порождая леность мышления. Однако, процесс взаимодействия Человека и Сети, который, без сомнения, носит резонансный характер, необратим, и главная задача - оптимизировать его, повысить его коэффициент полезного действия, чтобы это резонансное взаимодействие гармонизировало, а не разрушило взаимодействующие системы – привело к формированию Synergonet [5]-[6].

    Статистика использования того или иного слова в Internet даёт определённую информацию об его привлекательности и связях c другими словами и объектами, которые они обозначают. Мы обратились к нескольким наиболее известным поисковым системам и посмотрели количество ссылок, имеющихся в этих системах на слово «резонанс» на русском и английском языках. Результаты представлены в следующей таблице, составленной по материалам Internet от 16.03.2007.

 

                                                 Резонанс                          Resonance

 

Yandex.   Сайтов 2655. Страниц 1531371.  Сайтов 1502. Страниц 186835

Rambler   Сайтов 92842.  Докум.1686455.  Сайтов 15489. Докум. 278696

Апорт                                Докум.  339655                              Докум. 92751

Google                              Страниц 2 330000                  Страниц  41 400000

Yahoo                                              1 340000                                   15 200000

MSN                                                130446                                          2 166769.

 

    Анализ приведённых данных позволяет не только сравнить эффективность различных поисковых систем при изучении того или иного объекта, но и определить частоту встречи слова, в данном случае, слова «резонанс». Числа, характеризующие частоту встречи этого слова в Internet, поражают. Просмотреть все источники, в которых оно встречается, невозможно. Да это и не требуется. Ведь большинство из них содержит названия фирм и организаций, взявших на вооружение это звучное слово.

 

 

4. Смысл, вкладываемый в слово «резонанс» различными авторами.

 

«Когда исчезнут вещи и дела,

И даже след цивилизаций,

Вдруг прорастут из Времени Слова,

Осмыслив жадное пространство.

Всё, что копили миллионы лет,

Слова вдруг явят,

                              запах свой и цвет.

И форму, без которой слова- нет».

 

З. Е. Журавлёва[7]

 

    Слово «резонанс» в обыденном понимании означает взаимное усиление функционирования взаимодействующих структур и систем. Именно поэтому оно часто употребляется в переносном смысле. Выступление по радио или по телевидению может остаться незамеченным, а может вызвать «сильный резонанс», то есть значительную ответную реакцию. Согласованные действия многих людей тоже могут быть названы резонансными. Представление о резонансе возникает при определенном типе взаимодействия, когда эффективность совокупной  деятельности  взаимодействующих объектов или субъектов оказывается выше, чем эффективность действия каждого из них. В таком понимании резонанс становится синонимом синергии – кооперативного действия нескольких систем с взаимным усилением эффекта. Поэтому в последние годы изучение резонансных явлений неразрывно связано с Синергетикой – наукой о самоорганизации сложных систем [8].

 

. 5. Простейшее математическое уравнение, решение которого даёт представление о классическом резонансе.

 

    При научном изучении этого явления бытовое слово «резонанс» требовалось дополнить формулой, являющейся решением математической задачи, которая могла бы рассматриваться как модель одного или нескольких физических явлений. Так оно и произошло в действительности. Сначала слово «резонанс» описывало процесс усиления звука в помещениях. Затем это слово стало символом математической формулы, являющейся особым частным решением обыкновенного дифференциального уравнения второго порядка с зависящей от времени правой частью. Но одна и та же математическая формула может описывать различные реальные процессы. И это её свойство стало играть всё большую роль. Оказалось, что математическое уравнение, моделирующее явление резонанса, может описывать и усиление колебаний упругих конструкций, и колебания атомов и молекул, и колебания тока в контуре радиоприёмника, и качку корабля, и колебания маятника и многие-многие другие явления. [9-15].

    Математические формулы позволили достаточно строго определить понятие «резонанс», отождествив его с особым решением обыкновенного дифференциального уравнения второго порядка с постоянными коэффициентами при наличии внешних колебательных воздействий и при условии близости собственной частоты колебаний с частотой  внешнего воздействия.

    Это специфическое математическое уравнение имело столь широкую сферу практического применения, что слово «резонанс» в своём уже математически строгом определении стало общепринятым в различных физических, химических и биологических приложениях. При этом под резонансом понималось усиление колебаний системы под влиянием внешних воздействий при совпадении частот воздействия и собственных частот системы.

 

 

 

6. Внутренние резонансы в системах линейных дифференциальных уравнений с конечным числом степеней свободы

 

    Увеличение числа переменных в математическом описании линейных колебательных систем привело к необходимости изучения нового явления, возникающего при сближении внутренних собственных чисел системы или в случае, если совокупность собственных частот удовлетворяет определённому резонансному соотношению. Математические выражения, описывающие это явление, оказались во многом аналогичными формулам, описывающим явление классического резонанса. Так, например, в многомерных линейных системах было теоретически обнаружено явление вырождения собственных чисел, которое может считаться одним из проявлений внутреннего резонанса.

    Кроме того, при анализе нелинейных разложений решений систем обыкновенных дифференциальных уравнений вблизи стационарных точек появляется ещё одно понятие внутреннего резонанса, который возникает при определённом соотношении между собственными числами матрицы линейного члена разложения [9].

   

7. Параметрический резонанс

 

Математические формулы живут своей, независимой от приложений жизнью. Они усложняются и модифицируются, и эти модификации отражают всё более глубокие уровни взаимодействия объектов природы.

Линейное дифференциальное уравнение второго порядка, на примере которого впервые исследовался колебательный резонанс, является частным случаем динамической системы, описываемой системой нелинейных дифференциальных уравнений. В настоящее время колебательные явления, соответствующие этим уравнениям, согласно [10] могут быть классифицированы следующим образом .

              1) собственные колебания ,

2) вынужденные колебания,

3) автоколебания.

При этом, однако, нужно помнить, что решениями соответствующих уравнений могут быть не только колебательные, но и экспоненциально растущие  и затухающие движения. Их, следуя [8], будем называть модами.

 Собственными или свободными колебаниями или модами называют такие, которые происходят в системах, не содержащих источников энергии или эти источники не влияют на протекание процесса.

«Каждую динамическую систему можно характеризовать набором собственных форм колебаний (мод), называемых нормальными колебаниями (модами) Число нормальных колебаний зависит от числа степеней свободы системы. »[10]

Вынужденные процессы реализуются при наличии непосредственно зависящего от времени внешнего воздействия на динамическую систему

Именно при изучении вынужденных процессов (в частности колебаний) и появилась классическая модель резонанса. В классическом случае зависящее от времени воздействие входит в уравнение в виде отдельного аддитивного члена, чаще всего описывающего колебательный процесс. Резонанс возникает тогда, когда собственные (нормальные) моды системы близки или кратны частоте возмущающего воздействия.

    В случае, если внешнее, зависящее от времени, воздействие изменяет параметры системы, то обусловленные им возмущения системы называют параметрическими. Усложнение математических моделей колебательных явлений в сторону учёта дополнительной зависимости коэффициентов уравнений от времени приводило и приводит к модификации представлений о резонансе. Явление, названное параметрическим резонансом, было определено теоретически как особое свойство решения системы дифференциальных уравнений с зависящими от времени коэффициентами. Подробное математическое изложение теории параметрического резонанса можно найти в ряде монографий, среди которых следует отметить [10-15].

    Параметрический резонанс появляется как математическая модель реальных процессов, описываемых линейными дифференциальными уравнениями с периодическими коэффициентами, близкими к постоянным. При малом параметрическом возбуждении ранее устойчивая система может стать неустойчивой (и наоборот). Это имеет место обычно лишь для некоторых «критических» частот возбуждения, зависящих от нормальных мод невозмущённой системы уравнений. Теория параметрического резонанса позволяет определить спектры критических частот и разработать методы построения границ областей неустойчивости. К необходимости исследования явления параметрического резонанса приводят многие задачи современной техники и физики (динамическая устойчивость конструкций в строительной механике, задачи электротехники и радиотехники, ряд задач космической техники и небесной механики и др.)

В работе [15] В. Н. Челомей привёл несколько парадоксальных экспериментальных фактов, связанных с параметрическим резонансом.   Вот что он пишет: «Известно, что в статике центр тяжести механической системы стремится занять устойчивое положение, при котором потенциальная энергия её приобретает минимальное значение. Однако в динамике этот общеизвестный принцип иногда нарушается: центр тяжести системы может занимать динамически устойчивое положение, при котором потенциальная энергия приобретает значение, близкое к максимальному. Примерами тому могут служить устойчивое положение «перевёрнутого» маятника с пульсирующей точкой подвеса или система маятников  или вращающийся гироскоп и др.».          Во всех этих случаях в системах возникает параметрический резонанс.

    В технических приложениях часто используются «параметрические усилители» [10. C.76], то есть осцилляторы с одновременным использованием параметрического и классического резонанса.

 

8. Нелинейные резонансы в динамических системах. Влияние нелинейности на тип резонансной кривой. Основные соотношения между возмущающей частотой и резонансными частотами.

 

    Особой, бурно развивающейся областью динамики систем с конечным числом степеней свободы является теория нелинейных колебаний. Существование нелинейных членов в соответствующих уравнениях приводит даже в случае малых нелинейностей к новым эффектам. Резонансные явления сохраняются, но они приобретают существенные особенности, связанные с изменением типов резонансных кривых. Возникают субгармонические и супергармонические резонансы. Резонансное взаимодействие проявляется на частотах, в целое число раз больших или меньших частоты возмущающего воздействия. Эти типы резонансов часто возникают совместно с параметрическим резонансом, если в нелинейных дифференциальных уравнениях некоторые коэффициенты периодически зависят от времени.

    В системах связанных нелинейных осцилляторов возникают комбинационные резонансы, то есть возбуждённые колебания с основными частотами, связанными с частотой возмущения линейными соотношениями с целыми коэффициентами. Нелинейность способствует перекачке энергии колебаний из одних частот спектра в другие, что является очень важным для самоорганизации сложных транспортно-информационных систем.

 

9. Нелинейные резонансы и автоколебания.

 

    Одним из интенсивно развивающихся направлений нелинейной динамики является изучение нелинейных автоколебательных процессов, связанных с исследованием динамики активных сред.

Впервые понятие автоколебаний дано А. А. Андроновым [16-17].

«Автоколебаниями Андронов назвал  такие незатухающие колебания в автономной системе, которые устанавливаются и поддерживаются за счёт внутренних сил, зависящих от состояния движения самой системы, и амплитуда которых определяется свойствами системы, а не начальными условиями».[10]

В работах [10, 18-20] приводится несколько иное определение автоколебаний. «Автоколебательным следует называть диссипативные динамические системы, в которых могут возбуждаться и существовать колебания, удовлетворяющие двум требованиям:

1. независимости амплитуды установившихся колебаний от начального состояния системы в широком диапазоне, то есть существование в фазовом пространстве системы хотя бы одного аттрактора;

2. независимости или слабой зависимости спектра возбуждаемых колебаний от спектра источника».

При этом авторы предлагают не ограничиваться только автономными системами, но рассматривать и системы с периодическими источниками энергии.

    Возникновение и развитие автоколебаний происходит в условиях, когда потерявшая устойчивость динамическая система обладает определённым соотношением между собственными числами. (Этот процесс может считаться также специфическим проявлением внутреннего резонанса, так как мнимые части одинаково изменяющих свою действительную часть  собственных чисел имеют разные знаки, но одинаковую величину). Вместо экспоненциального или степенного удаления от стационарного состояния система переходит к новому – колебательному состоянию, которое в фазовом пространстве системы описывается в виде цикла.

    Цикл является простейшим аттрактором, отличным от стационарной точки - стабильного состояния. Аттрактором называется множество точек в фазовом пространстве, к которому стремятся со временем все соседние фазовые траектории из некоторой области, называемой областью притяжения.

    Дальнейшее развитие иерархии неустойчивостей, если они возникают, происходит, хотя и по различным, но вполне определённым бифуркационным сценариям, проходя бифуркации удвоения циклов (cценарий Фейгенбаума), рождения торов различной размерности и, наконец, перехода к хаотическим или стохастическим странным аттракторам [10, 21-28].

    На всех этапах функционирования автоколебательных систем возможны появления вынужденных и параметрических резонансов, которые приобретают новые, специфические свойства. Резонансы могут вызывать бифуркации динамических систем и приводить к хаотизации динамики системы. Так, например, в  работе [29] показано, что в нелинейном параметрическом усилителе возможна хаотизация колебаний. И наоборот, стохастические воздействия на систему могут вызвать регулярные резонансные колебания.

Во многих случаях автоколебательные системы синхронизируются с частотой вынуждающего воздействия или друг с другом [10].

   Таким образом, изучение нелинейных динамических систем привело к широкому обобщению математического понятия «резонанс», открытию его новых форм и неограниченному росту числа приложений, связанных с явлениями, которые с полным основанием можно было относить к резонансным, хотя ранее они резонансными не считались.  Одновременно расширилось и количество обиходных явлений, в которых стало использоваться слово «резонанс».

 

10. Резонансы в системах, описываемых комплексными уравнениями.

 

Следует указать на один математический аспект изучения резонансов в динамических системах. Если дифференциальные уравнения динамики исследуемого объекта рассматривать в терминах действительных переменных, то колебательные явления наблюдаются лишь как минимум  в уравнениях второго порядка (или двух уравнений первого порядка). При этом корни характеристического уравнения, соответствующие колебаниям, являются комплексными. Тем самым, даже оставаясь в рамках действительных функций, мы вынужденно получаем комплексные выражения.  Однако тот же результат может быть получен в рамках уравнения первого порядка только не для функции действительного, а для функций комплексного переменного. Поэтому общий анализ резонансов целесообразно проводить в рамках комплексных дифференциальных уравнений [13] при комплексных внешних воздействиях. При таком анализе выясняется, что вековые члены, соответствующие резонансам, появляются не только при мнимых, но и при произвольных комплексных  собственных значениях дифференциального оператора. Эти моды формально также могут считаться резонансными, однако реальное их проявление наблюдать достаточно сложно на фоне экспоненциального затухания или экспоненциального роста функций, описывающих решение. И всё же поиск такого рода «резонансов» представляет интерес. Ведь размножение и рост популяции живых объектов, а также фазовые переходы из одного стабильного состояния в другое описываются экспоненциально растущими функциями. Резонансные же возбуждения могут существенно изменить скорости развития этих процессов и тем самым явиться орудием управления динамикой системы в период её перехода  из одного состояния в другое.

 

11. Резонансные явления при произвольных внешних воздействиях.

 

    Резонансные явления проявляются и при произвольных внешних воздействиях на динамическую систему. В этом случае внешнее воздействие может быть представлено в виде интеграла или ряда Фурье, и в случае линейной системы каждая компонента Фурье воздействует на систему независимо. При этом резонансная компонента вызывает максимальный отклик. Наиболее отчётливо проявляется этот тип резонанса том случае, когда наибольшим коэффициентом в разложении Фурье внешнего воздействия обладает резонансная компонента. Таким образом, реакция системы, описываемой математически обыкновенными дифференциальными уравнениями, на произвольное внешнее воздействие всегда устроена таким образом, что резонансные компоненты усиливаются и в отклике системы играют большую роль, чем в воздействующем на систему сигнале.

    Математическое описание резонансных явлений обычно связывают только с дифференциальными уравнениями. Однако, очень часто динамические системы описываются дискретно, в виде некоторого итерационного процесса, который лишь в пределе переходит в непрерывный. Простейшим способом обнаружения резонансных явлений в итерационных системах может быть дискретизация дифференциальных уравнений, описывающих резонанс, и их решений. Возможно, на этом пути могут быть сделаны открытия, подобные открытию фрактальных структур в голоморфной геометрии [30].

 

12. О возможности степенных резонансов.

 

    Может быть предложено ещё одно важное направление в исследовании временных резонансов. В качестве примера рассмотрим простейшее комплексное дифференциальное уравнение первого порядка с экспоненциальным внешним воздействием. Предположим, что в этом уравнении произведена замена внутреннего  линейного времени на экспоненциальное время [31,32]. Тогда резонансное решение, записанное в форме колебаний, может быть переписано в виде степенных функций от экспоненциального (внешнего) времени. Тем самым  формально возникает принципиально новый тип резонансов – степенные резонансы. Особенностью резонансных решений в этом случае является появление квазистепенных многочленов содержащих логарифмы от экспоненциального времени.  

    Специфическая форма резонансных явлений, приводящая к хаотизации, возникает также при исследовании возмущений гамильтоновых систем (теория Колмогорова, Арнольда, Мозера) [10].

    Указанные формы резонансов являются временными резонансами, характеризуемыми взаимодействием частот и амплитуд линейных и нелинейных  колебаний .

 

 

 

 

Литература.

 

1. Сунгуров А. Ю. Резонансные взаимодействия в природе.- Синергетика и методы науки. Труды семинара. Под ред. М. А. Басина. СПб.: Наука. С. 431-433.

2. Баранцев Р. Г. Целостность общения.- XIV Международная конференция серии: «Нелинейный мир». Языки науки. Пущино. 3-7 июня 2006. Сборник тезисов. Под редакцией Г. Ю. Ризниченко. С. 18.

3. Басов Н. В. Риск - рефлексия и социальная самоорганизация» - XIV Медународная конференция серии:  «Нелинейный мир». Языки науки. Пущино. 3-7 июня 2006. Сборник тезисов. Под редакцией Г. Ю. Ризниченко. С. 19.

4. Басина Г. И., Басин М. А. Синергетика. Основы методологии. – СПб.: Норма. 2006.-56с. 

5. Басин М. А., Шилович И. И. Синергетика и Internet. Путь к Synergonet. СПб.: Наука. 1999. 72 с.

6. Басин М. А., Шилович И. И. Путь в Synergonet. СПб.: Норма. 2004. 128с.

7.Журавлёва З.Е. И услышал я иной голос. М.: Прогресс – Традиция, 1998. С.127. 193с.

8.Хакен Г.Синергетика. М.: Мир. 1980. 414с.

9. Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. Ижевск: Ижевская республиканская типография. 2000.400 с.

10. Ланда П. С. Нелинейные колебания и волны. М.: Наука. Физматгиз. 1997. 469 с.

11. Мандельштам Л. И. Лекции по колебаниям. Собр. трудов. Том 4. М.: Изд-во АН СССР. 1955.

12. Басин А. М. Качка корабля. М.: Транспорт. 1969. 272 с.

13. Арнольд В. И. Математические основы классической механики. М.: Наука. 1974. 432 c.

14. Якубович В. А., Старжинский В. М. Параметрический резонанс в линейных системах.- М.: Наука. Гл. ред. физ.-мат. литературы. 1987. 328с.

15. Челомей В. Н. Парадоксы в механике, вызываемые вибрациями.- В. Н. Челомей. Избранные труды. М.: Машиностроение 1989. С. 23-28. Материалы данной работы были доложены на заседании Отделения механики и процессов управления АН СССР 7. XII. 1982г., посвящённом 60-летию образования СССР, а также заседании Президиума АН СССР 27. I. 1983г.

16. . Андронов А. А., Витт А. А., Хайкин С.Э. Теория колебаний. Москва. Гостехиздат.1937; Физматгиз. 1959. Наука. 1981.

17. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука. 1984.

18. Ланда П. С., Дубошинский Я. Б. Автоколебательные системы с высокочастотными источниками энергии. – УФН. 1989. Т.158. В.4. С. 729-742.

19. Ланда П. С. Преобразование высокочастотных электрических колебаний в низкочастотные механические. Машиноведение 1988 №6. С. 90-95.

20. Ланда П. С. Электромеханические преобразователи автоколебательного типа. Вибротехника. 1991. №66.С.201-209.

21.                       Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в себя  Укр. Матем. Журнал. 1964 Т.26.№1 Сс.61-71.

22. Feigebaum M.J. Quantitative universality for a class of nonlinear transformations.J. Stat. Phys. 1978. V.19.№1. P. 25-52.

23. Feigebaum M. J. The onset spectrum of turbulence Phys. Let.1979 v/74A №6 Pp375-378

24.Nauenberg M.Rudnik J. Universality and the power spectrum at the onset of Chaos. Phys. Rev.B. 1981.V 24B№1Pp493-495

25. Kaneko K. Oscillations and doubling of torus  Progr.Theor.Phys.Japan. 1984.V.72№2 Pp. 202-215

26.Неймарк Ю.И. , Ланда П.С. Стохастические и хаотические колебания. Москва.Наука 1987

27. Анищенко В. С. Сложные колебания в простых системах. М.: Наука 1990.

28. Ruelle D., Takens F. On the nature of turbulence Comm. Math.Phys. 1971.V.20№2Pp.167-192.

29. Vavriv D. M, Ryabov V. R., Sharapov S.A., Ito H. M.Chaotic states of weakly and strongly nonlinear oscillators with quasiperiodic excitation. Phys. Rev. E. 1996 V.53.№1Pp.103-114

30. Милнор. Дж. Голоморфная динамика. Ижевск: НИЦ «Регулярная и хаотическая динамика». 2000. 320с.

31. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Ч.2.СПб.: Норма. 2002. 144с.

32. Басин М. А. внутреннее и внешнее время в динамике систем. Материалы Международной междисциплинарной научной конференции : «Синергетика в естественных науках» (Третьи Курдюмовские чтения). 19-22 апреля 2007 г. Ответственные за выпуск : Г.П. Лапина, Ю.В. Козловская. Тверь: Твер.глс.ун-т. 2007. С.147-151

 

 

 

 

 

 

 

 

 

 

 

 

Этюд 6

 

Бифуркации экспоненты окружности. Числа Басина.

 

    Фазовыми траекториями линейных динамических систем часто бывают замкнутые циклы, близкие к окружностям. В комплексной области  окружность радиуса  может быть описана формулой , где . Наиболее характерной нелинейной проблемой, поддающейся аналитическому решению, является, проблема определения динамики системы, логарифмы параметров динамики которой подчинены линейным закономерностям. Назовём экспонентой окружности замкнутую кривую в комплексной плоскости, получающуюся как отображение . Отделим в последнем выражении действительную часть от мнимой .

Найдём точки пересечения экспоненты окружности с осью абсцисс. Условие для их отыскания записывается в виде: . Отсюда следует, что при  . Последнее уравнение имеет счётное множество решений . Отсюда получаем . Решения последнего уравнения подчиняются ограничению  или  .

Если , тогда . Реальная координата экспоненты окружности в точках пересечения с осью абсцисс определяется по следующим формулам.

Если  то .

Если                       то .

Если то .

Если                       то .

Если рассматривать параметрическое семейство экспонент окружности, зависящее от параметра , то значения  являются бифуркационными. Если , то при достижении  появляются «из ничего» два отрицательных значения точек пересечения экспоненты окружности с осью абсцисс (корней) в области спиральных чисел, которые могут быть отождествлены в области алгебраических комплексных чисел с минус единицей (-1). Затем при увеличении  эти корни расщепляются и уходят от минус единицы – один вправо, а другой - влево. Таким образом, появляются и плавно изменяются четыре (два сдвоенных) корня. Этот процесс продолжается до тех пор, пока  не достигнет величины . Затем возникает новая бифуркация: в области спиральных комплексных чисел появляется два новых корня, имеющих в области алгебраических комплексных чисел одно и то же значение . Затем происходит расщепление каждого из этих корней на два, которые расходятся от единицы в разные стороны. Объяснение этих «фокусов» можно найти, если проследить характер изменения экспоненты окружности в зависимости от параметра  в комплексной плоскости. Рассмотрим динамику точки, соответствующей . Имеем .

То есть эта точка перемещается с изменением  по окружности с радиусом, равным единице, вращаясь тем быстрее, чем больше величина .  Эта окружность пересекает ось абсцисс в точках -1 и +1. Поэтому новые корни формируются именно в этих точках.

Таким образом, значения реальной координаты экспоненты окружности в точках пересечения с осью абсцисс при бифуркациях определяются по следующим формулам.

Если то .

Если                      то .

Если то .

Если                   то   .

Числа , являющиеся комбинацией трансцендентных и алгебраических иррациональных чисел - универсальные безразмерные величины, которые характеризуют бифуркационную динамику системы экспонент окружности.

В честь 100 – летия со дня рождения выдающегося учёного, профессора Абрама Моисеевича Басина, мы назвали их числами Басина.

Ввиду универсальности выполненного анализа эти числа в том или ином виде должны быть обнаружены при исследовании нелинейных динамических систем. (Смотри Этюды 7-9) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Этюд 7

 

Экспоненты окружности как фазовые кривые нелинейных динамических систем

 

  При исследовании динамических систем для определения динамики их интегральных параметров нами рекомендуется введение комплексного параметра целого, а также отыскание и решение комплексного обыкновенного  дифференциального уравнения, которому он удовлетворяет,

,                                                               (1)

где  может быть комплексной алгебраической переменной  или комплексной спиральной переменной  (смотри Этюд ). Фазовая траектория, являющаяся решением уравнения (1), может быть записана в виде

,                     (2)

где - значение алгебраической комплексной координаты фазовой траектории, проходящей через точку  в момент времени . Это же решение может быть записано и в спиральных переменных.

                          (3)

Введём новую функцию .

Тогда  уравнение (1) преобразуется к виду   или

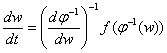                                                   (4)

Соответствующая фазовая траектория для переменной  имеет вид:

Таким образом, имея решение одного уравнения (1), мы можем построить класс производных нелинейных дифференциальных уравнений, связанных с данным, решения которых строятся на основе решения первого. 

  Нас в дальнейшем будет интересовать один важный частный случай выполненных преобразований.

  В качестве основного уравнения примем линейное комплексное уравнение.

.                                                                    (5)

Его решение может быть получено следующим образом: . Интегрируя обе части последнего равенства, получаем: . Экспонируя получившееся уравнение, получим .Если ,то , и фазовые траектории решения этого уравнения имеют вид

.                                                                (6).

Представим  . Тогда решение уравнения (5) примет форму:

                                                            (7)

Фазовые кривые представляют собой развёртывающиеся или скручивающиеся спирали либо сходящиеся к нулю, либо уходящие на бесконечность. В дальнейшем нас будет интересовать частный случай когда . В этом случае . Если считать, не теряя общности, что начальное значение неизвестной является действительным числом, то уравнение фазовой кривой имеет вид

.                                                        (8)

Точка фазовой кривой уравнения (5) в рассматриваемом частном случае движется по окружности радиуса .- то есть по циклической траектории. Далее примем, что связь между комплексными переменными  и  имеет вид:

.                                                                  (9).

Тогда уравнение, описывающее динамику переменной  примет форму

 или

                                                       (10)

 

 Циклические фазовые траектории динамической системы, описываемой этим уравнением,  имеют вид

Последнее выражение описывает траекторию в виде экспоненты окружности.(смотри Этюд №7). Таким образом, экспонента окружности является циклической фазовой траекторией некоторой динамической системы, описываемой комплексным обыкновенным дифференциальным уравнением (10). Бифуркации экспоненты окружности и связанные с ними бифуркационные числа Басина определяют динамику систем, описываемых этим уравнением. Однако, этим не исчерпывается класс уравнений, имеющих фазовые траектории типа экспоненты окружности. Известно, что в ряде динамических систем происходит бифуркации рождения цикла. Если переменные, входящие в эти системы рассматривать как логарифмы некоторых новых переменных, то для этих новых переменных получаются уравнения, для которых бифуркация рождения цикла превратится в бифуркацию рождения новой фазовой траектории, являющейся экспонентой окружности. Переход от циклической фазовой траектории к фазовой траектории в виде экспоненты окружности, по-видимому, является стандартным для самоорганизующихся информационно-транспортных систем, имеющих подсистемы с сильно отличающимися друг от друга, но связанными между собой масштабами описывающих их переменных.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                               Этюд 8 

Комплексный степенной многочлен как источник катастроф.

                                                           Аннотация

 

В работe [1,c.9], для аппроксимации событий, предшествующих катастрофе, предложено следующая функция от времени:

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba1.jpg

Комплексификация этой формулы и замена переменных позволили вскрыть степенную сущность представленной аппроксимации и определить линейное дифференциальное уравнение, решением которого она является.

                                                         Abstract


In work [1,p.9], for aproximation of occasions, preceding the catastrophe, is offered following function from a time:

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba2.jpg

Complexification of this formula and change of variable allowed to open degree essence of presented aproximation and define a linear differential equation, which deciding is it.

В работe [1,c.9], для аппроксимации событий, предшествующих катастрофе, предложено следующая функция от времени:

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba3.jpg

(1)

которая, по-видимому, обусловлена коллективным поведением одного и того же типа.
В настоящей заметке мы попытаемся указать простое дифференциальное уравнение, решением которого является функция, описываемая формулой (1).
Для этого преобразуем формулу (1) к виду:

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba4.jpgили

 

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba5.jpg

 

Введём обозначение

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba6.jpg

Тогда

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba7.jpg

или

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba8.jpg

Введём в рассмотрение комплексную величину

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba9.jpg,

(2),

реальной частью которой, в частном случае, является функция .
В общем случае сюда можно добавить конечное или бесконечное число степенных функций. Эта функция называется степенным полиномом её исследование вводит нас в степенную геометрию [2],[3].
Введём замену переменных

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba10.jpg

 

Тогда получаем простую формулу

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba11.jpg

(3)

с комплексными параметрами, где

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba12.jpg

может быть названо линейным временем в отличие от экспоненциального времени, описывающего соответствующий нелинейный процесс. [4]
А уравнение, которому удовлетворяет это решение, - это простое линейное дифференциальное уравнение второго порядка в линейном времени.

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba13.jpg

(4)

Это же уравнение может быть представлено в форме системы линейных уравнений первого порядка с двумя неизвестными

Описание: mhtml:file://C:\Documents%20and%20Settings\Маша\Мои%20документы\Downloads\Басин%20М.А.%20-%20Комплексный%20степенной%20многочлен%20как%20источник%20катастроф.mht!http://spkurdyumov.narod.ru/Basin/ba14.jpg

(5)

Полный качественный анализ решений этой системы выполнен в классических учебниках по дифференциальным уравнениям [5].
Комплексификация аппроксимационной формулы и замена переменных позволили вскрыть линейную сущность представленной аппроксимации и предложить её обобщение с целью определения всё более мелкомасштабных мод катастрофических событий.

Литература
1.Управление риском. Риск. Устойчивое развитие. Синергетика.
М.: "Наука"2000.432с
2. Басин М.А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно - информационные системы. Международная междисциплинарная научно-практическая конференция: "Современные проблемы науки и образования". Керчь, 27 июня - 4 июля 2001года. Материалы конференции .Часть1. Харьков 2001. С.12-13.
3.Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Наука. Физматлит. 1998. 288с.
4. Басин М.А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. Санкт -Петербург: "Норма" 2002. 144 с.
5. Арнольд В.И. Обыкновенные дифференциальные уравнения.Изд.3, перераб. и доп. -М.: "Наука" 1984.272с.

Конец формы

 

 

 

 

 

 

 

Этюд 9.

 

Экспонента окружности как фазовая траектория нелинейного итерационного соотношения.

 

.

 

    В настоящем этюде установлены критерии эквивалентности комплексного дифференциального уравнения первого порядка и нелинейного итерационного соотношения. Установлены условия, при которых точки, соответствующие решению итерационного соотношения, лежат на экспоненте окружности.

    При исследовании динамических систем может быть введён комплексный параметр целого и найдено и комплексное обыкновенное дифференциальное уравнение, которому он удовлетворяет:

.                                                    (1)

Здесь  может быть комплексной алгебраической переменной  или комплексной спиральной переменной . Семейство фазовых траекторий, являющихся совокупностью решений уравнения (1), может быть представлено в виде:

,-                  (2)

где - значение комплексной координаты фазовой траектории, проходящей через точку  в момент времени 0. Это решение может быть записано и в спиральных переменных:

.                        (3)

Построим итерационное соотношение, эквивалентное описанной динамической системе.

Разрешим равенства (2, 3) относительно :

.                                                 (4)

Предположим, что мы знаем состояние одномерной комплексной динамической системы в момент , соответствующий точке , и хотим определить состояние той же системы в момент . Тогда, воспользовавшись предыдущими формулами, получим:

.          (5)

Введём понятие оператора :

.                                 (6)

Оператор порождает итерационный процесс и указывает преобразование состояния динамической системы в момент времени  в её состояние  в момент времени .

.                                                        (7)

Последнее уравнение описывает дискретную по отношению к времени систему, полностью эквивалентную непрерывной динамической системе.

    Существует ещё один способ перехода от непрерывной модели к дискретной. Вместо системы (1) запишем приближённую систему

,                                               (8)

 которая, после ряда преобразований, приводится к виду:

.                               (9)

Операторы ине эквивалентны и один сходится к другому при стремлении  к нулю.

    Рассмотрим один практически важный частный случай. В качестве основного примем линейное комплексное уравнение

.                                                                    (10)

Решение этого уравнения имеет вид:

.                                    (11)

Окончательно получаем итерационное соотношение:

.                                                      (12).

Тем самым, в случае постоянного временного интервала итерационный процесс первого типа, удовлетворяющий равенствам (5-7), представляет собой геометрическую прогрессию в области комплексных чисел. Если величина  является мнимой, то все члены ряда (12) лежат на окружности радиуса.

Итерационный процесс (9) в нашем частном случае примет вид:

.                                                (13)

Формулы (12) и (13) совпадают лишь в пределе при . В случае конечных значений  итерационные процессы отличаются друг от друга тем более, чем больше модуль величины .

Далее введём в рассмотрение новую комплексную переменную:

.                                              (14)

Тогда уравнение (1) преобразуется к виду:

 

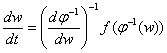,-                                             (15)

а соответствующие итерационные процессы будут иметь следующий вид:

.                                   (16)

Последнее уравнение описывает итерационный процесс, эквивалентный уравнению (15).

Другой, приближённый вариант итерационного процесса, соответствующий  урав/нению (15). имеет вид:

.                                                     (17)

В рассмотренном ранее частном случае линейного дифференциального уравнения примем, что зависимость  новой переменной от старой имеет  вид .

Тогда итерационное соотношение (12) после ряда преобразований примет форму

.                                                      (18)

Итерационный процесс (18) в правой своей части содержит степенную функцию с комплексным показателем степени. Для адекватного описания таких функций необходимо ввести представление о спиральных комплексных числах, которое даётся в Этюде 11. В случае, если величина  представляет собой мнимое число, все точки итерационного процесса (18) лежат на одной из экспонент окружности, параметры которой определяются значением . Бифуркации экспоненты окружности и связанные с ними Числа Басина в  этом случае также определяют качественные изменения динамики исследуемой системы.

    И, наконец, второй тип итерационного процесса даёт нам следующее равенство:

.                                                 (19)

В данном случае мы также имеем в правой части уравнения (19) степенную функцию с комплексным показателем степени, однако члены итерационного процесса ложатся на экспоненту окружности только в случае мнимых значений и стремления модуля этой величины к нулю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

/

 

Этюд 10

 

Многомерные степенные комплексные системы итерационных соотношений. Экспонента окружности как одна из форм фундаментального решения системы.

 

 

 

При решении нелинейных многомерных проблем динамики сложных систем особую роль играют комплексные операторы, которые могут быть названы степенными. Рассмотрим символьное многомерное итерационное соотношение:

/.                                                               (1)

Здесь  - совокупность спиральных комплексных координат;

-                                         (2)

линейный комплексный оператор, элементами которого являются алгебраические комплексные числа (смотри Этюд 11). Соотношение (1) соответствует системе уравнений:

.                                                         (3)

Прологарифмируем левую и правую части  равенства (3):

                                                     (4)

или в векторно - операторном виде:

.                                                         (5)

Введём следующее обозначение:

.                                                   (6)

Тогда уравнение (5) запишется в виде:

,                                                              (7)

а равенство (4) –в форме:

.                                                        (8)

Введём в рассмотрение комплексное конечномерное аффинное векторное пространство. Вектором будем счи/тать совокупность алгебраических комплексных чисел: /

.                                           (9)

Считаем, что пространство отнесено к определённым ортам:

.                                                  (10)

Так что

.                                    (11)

Равенства (7), (8) назовём линейным преобразованием вектора  к вектору.

Если определитель матрицы  отличен от нуля, то, решая уравнения (7), (8) относительно , получаем

,                                                 (12)

где матрица  имеет элементы

.                                                (13)

Здесь -определитель матрицы , а  алгебраические дополнения его относительно элементов . Введём в рассмотрение новые орты:

.                                                   (14)

Связь между старыми и новыми ортами выражается с помощью соотношений:

.                                                    (15)

При этом определитель матрицы

/                                                          (16)

считаем не равным нулю. Если некоторый вектор  в системе координат с ортами (10) имел составляющие , то в новой системе координат он будет иметь другие составляющие

,                                  (17)

которые выражаются через предыдущие при помощи соотношения:

.                                             (18)

Здесь матрица  транспонирована по отношению к матрице . Если мы имеем некоторый линейный итерационный процесс, который в первоначальной системе координат выражался формулой (7), то в новой системе координат это  же преобразование будет выражаться формулой

,                                                    (18)

где

.                                                  (19)

Матрица

                                                    (20)

называется подобной матрице . /Подобные матрицы равносильны в том отношении, что они представляют одно и то же преобразование пространства, но выраженное в различных координатных системах. Если определитель матрицы отличен от нуля, то среди матриц  имеются диагональные матрицы [1], у которых отличны от нуля только диагональные члены. В случае выбора преобразования  таким образом, что матрица  станет диагональной, соотношение (18) разобьётся на комплексные одномерные итерационные соотношения типа

,                                                       (21)

где -диагональные члены матрицы .

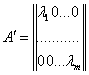.                                                        (22)

Для отыскания соответствующей матри/цы  и диагональных членов матрицы  выпишем следующее равенство:

                                                           (23)

или в координатной форме

.                                                    (24)

Если рассматривать элементы  как составляющие некоторого вектора , то можно записать равенство (24) в виде векторного равенства

.                                              (25)

«Мы видим таким образом, что разыскание матрицы , которая приводит матрицу  к диагональной форме сводится к разысканию таких векторов , которые воспроизводятся с точностью до численного множителя в результате линейного преобразования, определяемого матрицей . Этот факт является алгебраическим аналогом того факта современной квантовой механики, согласно которому матричная механика Гейзенберга по существу равносильна волновой механике Шредингера.

Согласно первой точке зрения, существенным вопросом является задача приведения некоторой матрицы (бесконечной) к диагональной форме. Что же касается волновой механики, то здесь существенным вопросом является задача отыскания таких векторов (в пространстве с бесчисленным множеством измерений), которые бы воспроизводились с точностью до численного множителя в результате некоторого линейного преобразования. Предыдущие соображения мы назвали алгебраическим аналогом потому, что, ограничиваясь пр//остранством с конечным числом измерений, мы приводим наши задачи к чисто алгебраическим задачам. В более же сложных случаях с бесчисленным множеством измерений мы существенно выходим из рамок обычной алгебры и нуждаемся в аппарате анализа» [1].

Система (24) или (25) может быть записана в виде:

.                                                   (26)

Здесь  - единичная матрица. Для получе/ния отличного от нуля результата определитель матрицы  должен быть рав//ен нулю, то есть:

.                                               (27)

Таким образом, мы получили характеристическое комплексное алгебраическое уравнение -ого порядка относительно, которое имеет ровно  комплексных решений.  Предположим, что эти решения различны. Найдя все значения , мы можем построить матрицу

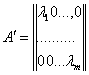                                            (28)

и вместо системы итераций (12) решать одномерные итерационные соотношения (21), которые уже  рассматривались нами в Этюде №9.

Нам осталось теперь определить с точностью до произвольного не равного нулю комплексного постоянного множителя элементы матрицы . Для этого в системе уравнений (26) зададим произвольно какую-либо координату вектора  и перенесём соответствующие ей члены левой части  уравнения (26) в правую часть, отбросив одно из уравнений. Если в этом случае получившаяся неоднородная система уравнений на единицу меньшего порядка имеет определитель, не равный нулю, то решение определяется по формулам Крамера [1]. Эта процедура повторяется для всех значений . Вернёмся к системе итерационных соотношений (21). Подставляя последовательно в правую часть значения  вплоть до , получим

.                                                   (29)

Равенство (29) определяет фундаментальное решение системы итерационных соотношений (7). Введём новые комплексные переменные:

.                                                       (30)

Тогда система (29) запишется в виде: 

.                                             (31)

Потенцируя (31) , получим:  

                         .                                                (32)

Если  комплексная величина с модулем равным единице, то значения   при любых целых значениях  лежат на экспоненте окружности (смотри Этюд №9). Таким образом, экспонента окружности, бифуркации которой были рассмотрены нами в Этюде №9, является одной из  фундаментальных форм фазовой траектории для достаточно общей системы степенных итерационных соотношений. В ортогональной системе координат можно ввести понятие экспоненциального вектора:

  .                                                    (33)

Тогда соотношение (32) может быть записано в символьном виде:

.                                                    (34)

Соотношение (31)  может быть записано в форме:

.                                              (35)

Последнее равенство записано уже в терминах аффинных векторов и классических матриц. Вернёмся в соотношении (35) к первоначальной системе координат, воспользовавшись соотношениями (18)-(20)

                                         (36)

 или

.                                                            (37)

Потенцируя (37), получим решение системы (1) в символьной форме

.                                                            (38)

Между координатами экспоненциального  вектора осуществляется связь согласно соотношению

.                                                                (39)

Или в координатной форме

 

.                                                        (40)

Литература

1.Смирнов В. И. Курс высшей математики для техников и физиков . Том 3  ГИТТИ М.-Л.     1933 73

 

\\\

 

Этюд 11

 

Алгебраические и спиральные комплексные числа.

 

 

Введём одну из возможных модификаций комплексных чисел, использование которой позволяет, если это необходимо, рассматривать степенные функции комплексного переменного с комплексными показателями степени как однозначные функции,  следовательно, применить к их исследованию весь аппарат современного анализа.

    Любое комплексное число имеет, как минимум, два возможных представления: алгебраическое -  и экспоненциальное - . При этом каждому алгебраическому представлению комплексного числа соответствует счётное множество экспоненциальных представлений, в которых величина отличается на

Предположим, следуя Б. Риману[1] и Г. Вейлю [2], что имеется некоторая винтовая спиральная структура, пересекающая комплексную плоскость по положительной оси со стремящимся к нулю шагом  [3-5]. Каждо й точке такой спиральной винтовой поверхности приведём в соответствие некоторое спиральное комплексное число, которое может быть описано формулой . Величина  характеризует расстояние от точки спиральной поверхности до оси, перпендикулярной плоскости  и проходящей через точку . При такой геометрической интерпретации все точки, соответствующие спиральным комплексным числам, имеющим значения , отличающиеся на, лежат на одной прямой, проекцией которой на плоскость  является одно алгебраическое комплексное число , где . Каждому спиральному комплексному числу соответствует  одно алгебраическое комплексное число. Но каждому алгебраическому комплексному числу соответствует счётное множество спиральных комплексных чисел. Введём в рассмотрение ещё одну комплексную плоскость, которая соответствует полю алгебраических комплексных чисел, которые получатся, если формально взять операцию логарифма от каждого спирального числа . Функция  и обратная ей  являются взаимно однозначными функциями, отображающими друг на друга область определения спиральных чисел  и алгебраическую комплексную плоскость. Каждая горизонтальная полоса области  высотой  соответствует одному листу спирали.

    Далее рассмотрим в области совокупность взаимно-однозначных комплексных линейных отображений . В качестве коэффициентов такого отображения примем поля алгебраических комплексных чисел. Эти отображения являются взаимно однозначными во всех точках , кроме точки .

Введём ещё одно взаимно однозначное отображение комплексной плоскости на область спиральных комплексных чисел . Тогда получим взаимно однозначное отображение

Константа  также лежит в области определения спиральных чисел. Таким образом, многозначная степенная функция с комплексными показателями степени при рассмотрении её в области определения спиральных чисел становится взаимно однозначной. И с ней можно осуществлять все операции так же, как со степенными функциями, лежащими в области действительного переменного. Введение спиральных комплексных чисел обеспечивает условия для развития степенной геометрии с алгебраическими комплексными показателями степени.

При этом, в некоторых случаях, когда  является целым числом, можно работать с проекциями спиральных чисел на комплексные плоскости  .

    Оставаясь в рамках алгебраических комплексных чисел, мы рискуем потерять возможные элементы множества точек, на которые отображает степенная функция данное алгебраическое комплексное число. Возникают многозначные и даже бесконечнозначные функции, а с ними понятие вероятности выбора той или иной ветви многозначного отображения.

Существует проблема взаимоотношений построенной математической конструкции с реальными объектами, которые описываются при помощи той или иной математической конструкции. Мы вовсе не всегда «видим» спиральное число, чаще «наблюдается» его проекция на комплексную плоскость  и описываемая обычными степенными функциями комплексных чисел динамика системы «кажется» нам бифуркационной.

Так как совокупность построенных однозначных степенных функций является одной из форм экспоненты алгебры линейных отображений над комплексными числами, то в области определения спиральных чисел естественным образом вводится умножение спиральных чисел как спиральный аналог сложения степеней экспонент соответствующих алгебраических комплексных чисел. Аналогичное утверждение может быть сделано относительно умножения степенных функций некоторой спиральной переменной .

Пусть  -две степенные функции спиральной переменной .

Тогда функция  также будет однозначной степенной функцией от .

, где .

Аналогичным образом доказывается, что возведение степенной функции в комплексную степень порождает новую степенную функцию со степенью, равной , и коэффициентом, представляющим собой спиральное число, являющимся коэффициентом первоначальной функции, возведённым в степень .

Значительно сложнее ввести понятие сложения спиральных комплексных чисел, а следовательно, сложения степенных мономов. Эту проблему можно назвать проблемой Лагранжа [6]. Наметим лишь пути решения указанной задачи.

Пусть даны два спиральных числа или две степенные функции спиральной переменной  . Определить сумму этих спиральных чисел. В области спиральных чисел такое определение дать довольно сложно. Однако, мы можем спроектировать оба числа на плоскость алгебраических комплексных чисел и в этой плоскости вычислить уже сумму двух соответствующих им алгебраических комплексных чисел. Если считать, что сумма алгебраических комплексных чисел является проекцией спирального комплексного числа, являющегося суммой спиральных комплексных чисел, то наше определение позволяет с точностью до бесконечного множества значений , отличающихся друг от друга на , такую сумму определить. Возникает проблема выбора одного из бесконечного множества имеющихся значений. Более подробно эта важная проблема, на наш взгляд, имеющая решение, будет рассмотрена позднее.

 

Литература

 

1. Riemann B. Theorie der Abelschen Funktionen. Borhardt’s Journ. für reine und angewandte Math. 54.). 1857. Werke. Leipzig 1876.S.81-135.

2. Weyl H. Die Idee der Riemanischen Fläche. Leipzig-Berlin. 1913 (1-ste Aufl.). 1923 (2-te Aufl.). Stuttgart.1953 (3-te Aufl.)

3.Шабат Б. В.Введение в комплексный анализ. Ч.1. Функции одного переменного. М. 1976

4.Стоилов С. Теория функций комплексного переменного. В 2 томах. Основные понятия и принципы. М.:1962.

5. Басин М. А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно-информационные системы. Международная междисциплинарная научно-практическая конференция: «Современные проблемы науки и образования». Керчь 27.06-4.07.2001. Ч.1 Харьков. 2001. С.12-13.

6.Арнольд В.И., Авец А. Эргодические проблемы классической механики. Ижевск 1999

 

 

 

Этюд 12.

Комплексная динамика живого. .

 

 

     Классическая механика базируется на втором законе Ньютона, символизируемом одномерным дифференциальным уравнением второго порядка [1]:

.                                                           (1)

Все достижения современной теории неживых систем и основанных на ней технологий вплоть до квантовой механики и теории относительности построены на обобщении и  модификации уравнения (1).

     Возникает вопрос, существует ли такое же фундаментальное уравнение, которое может стать базой для создания математической теории живых систем. При этом его решения должны описывать такие свойства живого как рост, размножение, неоднозначность поведения и самоорганизацию. В настоящей статье сделана попытка отыскания такого уравнения.

     Рассмотрим дифференциальное уравнение первого порядка:

,-                                                               (2)

где  может быть комплексной алгебраической переменной  или комплексной спиральной переменной  [2]. Рассмотрим некоторые особенности этого уравнения, дающие ему право претендовать на фундаментальное значение при математическом исследовании живых систем. Фазовая кривая, являющаяся решением уравнения (2), может быть записана в виде:

,                     (3)

где - значение алгебраической комплексной координаты фазовой траектории, проходящей через точку  в момент времени . Это же решение может быть записано и в спиральных комплексных переменных:

.                          (4)

При этом решение может быть многозначным и даже бесконечнозначным.

     Введём новую функцию . Тогда  уравнение (2) преобразуется к виду:

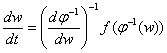.                                                   (5)

Соответствующая фазовая кривая для переменной  имеет вид:

Таким образом, имея решение одного уравнения (2), мы можем построить класс производных нелинейных дифференциальных уравнений, связанных с данным, решения которых строятся на основе решения первого.

     Применительно к живым системам нас в дальнейшем будет интересовать один важный частный случай выполненных преобразований. В качестве основного уравнения примем линейное комплексное уравнение [2-3]

,                                                                    (6)

решение которого легко получается в аналитическом виде. При  имеем . Интегрируя левую и правую части последнего равенства, получаем: . Потенцируя получившееся уравнение, получим . Если , то . Отсюда решения этого уравнения имеют вид:

.                                                                (7).

Представим коэффициент  в виде суммы реальной и мнимой части . Тогда решение уравнения (6) примет форму:

.                                                            (8)

Фазовые кривые представляют собой развёртывающиеся или скручивающиеся спирали в комплексной области, либо сходящиеся к нулю, либо уходящие на бесконечность. Это общее решение характеризует устойчивость стационарных точек как при моделировании неживых, так и живых систем. Если принять , то равенство (8) описывает экспоненциальный рост популяции, который может быть вызван, например, периодически происходящим делением клеток.

     Особый интерес представляет частный случай равенства (8), когда . В этом случае . Если считать, не теряя общности, что начальное значение неизвестной является действительным числом , то уравнение фазовой кривой имеет вид:

.                                                        (9)

Фазовой кривой уравнения (6) в рассматриваемом частном случае является окружность радиуса . Тем самым, в данном частном случае решение уравнения (2) может описывать циклические процессы, как в живой, так и в неживой природе. Разделение действительной и мнимой частей уравнения (6) с последующей заменой переменных приводит к линейному варианту уравнения (1), что позволяет считать уравнение (2) в некотором смысле обобщением уравнения Ньютона (1). Далее примем, что связь между комплексными переменными  (алгебраическая переменная) и (спиральная переменная) [2] имеет вид:

.                                                                  (10)

Тогда уравнение, описывающее динамику переменной , примет форму:

.                                                       (11)

Если  , то уравнение (11) для действительных значений переменой  наряду с известным логистическим уравнением [3] может быть использовано для описания ограниченного некоторым пределом роста популяции организмов, отдельного организма или разделившейся клетки [4, 5]. Однако, на наш взгляд, значительно больший интерес при исследовании динамики сложных иерархических систем представит в будущем другой частный случай этого уравнения, соответствующий чисто мнимому значению величины. В этом случае циклические фазовые кривые динамической системы, описываемой этим уравнением, имеют вид 

.       (12)

Такие кривые будем называть экспонентами окружности. Рассмотрим особенности этих кривых более подробно. В алгебраической комплексной плоскости  окружность радиуса  может быть описана формулой , где  Назовём экспонентой окружности замкнутую кривую в комплексной плоскости, получающуюся как отображение . Отделим в последнем выражении действительную часть от мнимой

.                                           (13).

Найдём точки пересечения проекции экспоненты окружности на комплексную плоскость  с осью абсцисс. Число этих точек конечно и растёт с ростом величины . Условие для их отыскания записывается в виде: . Отсюда следует . Последнее уравнение имеет счётное множество решений . Отсюда получаем . Решения последнего уравнения подчиняются ограничению  или  .

Если , тогда . Реальная координата экспоненты окружности в точках пересечения с осью абсцисс определяется по следующим формулам

Если  то .

Если                       то .                                  (14)

Если то .

Если                       то .

Если рассматривать параметрическое семейство экспонент окружности, зависящее от параметра , как фазовую плоскость уравнения (11) при , то значения  являются бифуркационными. Если , то при достижении  появляются «из ничего» два отрицательных значения точек пересечения экспоненты окружности с осью абсцисс (корней) в области спиральных чисел, которые могут быть отождествлены при проектировании на плоскость алгебраических комплексных чисел с минус единицей (-1). Затем при увеличении  эти корни расщепляются и уходят от минус единицы – один вправо, а другой - влево. Таким образом, появляются и плавно изменяются четыре (два сдвоенных) корня. Этот процесс продолжается до тех пор, пока  не достигнет величины . Затем возникает новая бифуркация: в области спиральных комплексных чисел появляется два новых корня, имеющих в области алгебраических комплексных чисел одно и то же значение . Затем происходит расщепление каждого из этих корней на два, которые расходятся от единицы в разные стороны. Объяснение этих «фокусов» можно найти, если проследить характер изменения экспоненты окружности в зависимости от параметра  в комплексной плоскости. Рассмотрим динамику точки, соответствующей . Имеем . То есть эта точка перемещается с изменением  по окружности с радиусом, равным единице, вращаясь тем быстрее, чем больше величина . Эта окружность пересекает ось абсцисс в точках -1 и +1. Поэтому новые корни формируются именно в этих точках.

     Таким образом, бифуркационные значения реальной координаты экспоненты окружности в точках пересечения с осью абсцисс определяются по следующим формулам:

Если то .

Если                      то .                                   (15)

Если то .

Если                   то   .

Числа , являющиеся комбинацией трансцендентных и алгебраических иррациональных чисел - универсальные безразмерные величины, которые характеризуют бифуркационную динамику системы экспонент окружности. В честь 100 – летия со дня рождения выдающегося учёного, профессора Абрама Моисеевича Басина, мы назвали их числами Басина. Ввиду универсальности выполненного анализа эти числа в том или ином виде должны быть обнаружены при исследовании нелинейных динамических уравнений, возникающих при математическом исследовании сложных иерархических систем.  При малых значениях) фазовые кривые становятся близкими к окружностям с общим центром в точке с комплексной координатой, равной 1. Это соответствует  линейным колебаниям около некоторого стационарного состояния. Переход от фазовой кривой в виде окружности к фазовой кривой в виде экспоненты окружности, по-видимому, должен являться стандартным для биологических и социальных систем, имеющих элементы и подсистемы с сильно отличающимися друг от друга, но связанными между собой масштабами описывающих их переменных. Каждая система такого типа обычно состоит из очень большого числа элементов, формирующих подсистемы различных масштабов, и функционирует в поле, формируемом аналогичными структурами и внешней средой [6], масштабы зоны влияния которого многократно превышают масштаб системы. Числа Басина формируют дискретную последовательность, соответствующую итерационному процессу, отражающему двойственность непрерывного и дискретного описания динамической системы.  В сборнике [7] на примере большого количества иерархических систем (в том числе биологических и социальных) выведена закономерность, связывающая характерные параметры системы, её элементов и подсистем с параметрами поля, сопряжённого с системой. Произведение соответствующих характерных масштабов параметров элементов системы или её подсистем и совокупности систем, формирующих поле, оказалось близким к квадрату характерного масштаба аналогичного параметра самой системы. Эта же закономерность наблюдается в структуре чисел Басина. Если принять характерный масштаб системы за единицу, то экспонента окружности, являющаяся циклической фазовой кривой комплексного уравнения (11), пересекает действительную ось в точках, реальные координаты которых удовлетворяют установленной в [7] эмпирической закономерности. Последний факт даёт основание для предположения о том, что уравнение (11) , в случае мнимого значения коэффициента описывает фундаментальные параметры управляющей подсистемы, обеспечивающей устойчивое состояние сложной иерархической системы (например, биологической или социальной). В этом случае могут обеспечиваться симметрия и целостность самой  системы, её элементов и подсистем  и её поля. Ранее такая подсистема была названа нами контроллером. В монографиях [2], [4], [5] в соответствии с триадическим принципом Р.Г. Баранцева [8],[9] нами рассматривалась триада

 

                                                                 Поле

                                                                  /     \

                                                   Структура---Контроллер

 

Если высказанная гипотеза верна, то числа Басина должны определять структурообразование как внутри, так и вне биологических и социальных систем и являться базой для определения основных параметров контроллера системы.

Рассмотрим ещё одну возможную модификацию уравнения (2), позволяющую более чётко выявить двойственность дискретного и непрерывного описании сложных систем, отражающую реальную двойственность в биологических и социальных системах.

Построим итерационное соотношение, эквивалентное описанной динамической системе (2). Разрешим равенства (3, 4) относительно :

.                                                 (16)

Предположим, что мы знаем состояние одномерной комплексной динамической системы в момент , соответствующее точке , и хотим определить состояние той же системы в момент . Тогда, воспользовавшись предыдущими формулами, получим:

.        (17)

Введём понятие оператора :

.                                 (18)

Оператор порождает итерационный процесс и указывает дискретное преобразование состояния динамической системы в момент времени  в её состояние  в момент времени:

.                                                        (19)

Последнее уравнение описывает дискретную систему, полностью эквивалентную непрерывной динамической системе. Существует ещё один способ перехода от непрерывной модели к дискретной. Вместо системы (2) запишем приближённую систему

,                                               (20)

 которая, после ряда преобразований, приводится к виду:

.                               (21)

Операторы ине эквивалентны и один сходится к другому при стремлении  к нулю. Используя, в частном случае, уравнение (6) , получаем вместо (20) итерационное соотношение:

.                                                      (22).

Тем самым, в случае постоянного временного интервала итерационный процесс первого типа, удовлетворяющий равенствам (17-19) представляет собой геометрическую прогрессию в области комплексных чисел. Если величина  является мнимой, то все члены ряда (22) лежат на окружности радиуса.Итерационный процесс (21) в нашем частном случае примет вид:

.                                                (23)

Формулы (22) и (23) совпадают лишь в пределе при .

В случае конечных значений итерационные процессы отличаются друг от друга тем более, чем больше модуль величины . Далее, как и ранее, введём в рассмотрение новую комплексную переменную:

.                                              (24)

Тогда соответствующие итерационные процессы будут иметь следующий вид:

.                                   (25)

Последнее уравнение описывает итерационный процесс, эквивалентный уравнению (5).

Другой, приближённый вариант итерационного процесса, соответствующий  уравнению (5) имеет вид:

.                                                     (26)

В рассмотренном ранее частном случае линейного дифференциального уравнения, как и ранее, примем, что зависимость новой переменной от старой имеет  вид .

Тогда итерационное соотношение (26) после ряда преобразований примет форму

.                                                      (27)

Итерационный процесс (27) в правой своей части содержит степенную функцию с комплексным показателем степени. Для адекватного описания таких функций нами ранее было введено представление о спиральных комплексных числах [2]. В случае если величина  представляет собой мнимое число, все точки итерационного процесса (27) лежат на одной из экспонент окружности, параметры которой определяются значением . И, наконец, второй тип итерационного процесса даёт нам следующее равенство

.                                                 (28)

В данном случае мы также имеем в правой части уравнения (28) степенную функцию с комплексным показателем степени, однако члены итерационного процесса ложатся на экспоненту окружности только в случае мнимых значений и стремления модуля этой величины к нулю.

Значительный интерес при исследовании динамики биологических систем представляет частный случай равенства (27), когда модуль  равняется единице, а показатель степени представляет собой правильную дробь с числителем, равным единице. В этом случае в области алгебраических комплексных чисел правая часть уравнения (27) становится многозначной функцией и число её значений на каждом шаге итерации равно знаменателю показателя степени. Тем самым на каждом шаге итераций число значений функции размножается, при этом модуль функции сохраняет значение равное единице. Это свойство итерационного процесса (27) совместно с уравнением (11) использовано нами для создания принципиально новой модели размножения и роста биологических объектов[4],[5].

Другим законам подчиняется рост человеческой популяции [5, 10]. Однако, и в этом случае было найдено дифференциальное уравнение первого порядка, описывающее динамику роста числа людей за весь период существования человечества, включая происходящий в настоящее время демографический переход. Оно является частным случаем уравнения (2). Комплексификация предложенного в [10] уравнения и приведение его к форме уравнения (2) позволила нам не только упростить вид этого уравнения, но и получить дополнительное уравнение, которое, по нашему мнению, характеризует динамику информации, управляемой растущим в объёме человечеством [5].

Таким образом, уравнение (2), его частные случаи и модификации с большим успехом используются для описания роста и размножения живых объектов от клетки до популяции. Кроме того, исследование этого уравнения позволило определить новый тип нелинейных  динамических систем со специфической формой бифуркационного поведения и найти универсальный набор иррациональных действительных чисел, названных числами Басина, которые, по нашему мнению, могут определять условия формирования сложных иерархических систем, в том числе, биологических и социальных.

 

Литература.

1.    Арнольд В. И. Математические методы классической механики. М.: Наука. 1974.432 с.

2.    Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. СПб.: Норма. 2002. 144 с.

3.    Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука. 1984.272 с.

4.    Басин М.А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Часть 1. СПб.:Норма.2000. 168 с.

5.    Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. Спб.: Норма. 2003.260с.

6.    Любищев А. А., Гурвич А.Г. Диалог о биополе. Составители: В. А. Гуркин, А.Н.Марасов, Р.В. Наумов. Ульяновск: Ульяновский государственный педагогический университет.1998. 208 с.

7.    Иванов-Ростовцев А. Г., Колотило Л. Г., Тарасюк Ю. Ф. Шерстянкин П.П. Самоорганизация и саморегуляция природных систем (модель, метод и основы теории D-SELF. Под редакцией, с предисловием,комментариями и заключением академика РАН К. Я. Кондратьева. СПб.: Русское географическое общество. 2001. 216 с.

8.    Баранцев Р. Г. Синергетика в современном естествознании. М.:Едиториал УРСС. 2003. 144 с.

9.    Баранцев Р. Г. Становление тринитарного мышления. М.-Ижевск: НИЦ «Регулярная и хаотическая механика». 2005. 124 с.

10.                         Капица С.П.. Общая теория роста человечества: сколько людей жило, живёт и будет жить на Земле. М.: Наука.1999. 190 с.

                                                                         

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                    Этюд 13

 

 

Введение внутреннего и внешнего времени в теорию динамических систем

 

    В работе рассмотрен класс комплексных конечномерных динамических систем, возникающих или исчезающих в определённый момент времени. При их построении использовано представление о внутреннем (линейном) и внешнем (экспоненциальном) времени. Установлена связь между представлениями систем обыкновенных дифференциальных уравнений в терминах внутреннего и внешнего времени. Результаты работы позволяют более адекватно описывать процесс рождения и разрушения сложных систем, в том числе живых организмов. В случае введения экспоненциального времени в систему линейных дифференциальных уравнений решения преобразованной системы представляют степенные многочлены от новой переменной. 

   

    Для описания конечномерных динамических систем во многих случаях используются системы нелинейных обыкновенных дифференциальные уравнений:

,                                                (1)

 

где  - нелинейный оператор,  - -мерный вектор, описывающий состояние исследуемой динамической системы. Формально не усложняя проблемы, предположим, что компоненты вектора  и оператор  комплексные. При рассмотрении многих проблем динамики решение системы дифференциальных уравнений существует в бесконечном диапазоне изменения времени (). Следовательно, большинство реальных систем и структур, имеющих конечный период существования, описывается в рамках дифференциальных уравнений с регулярными коэффициентами без учёта их возникновения и разрушения.

Поставим задачу отыскания такого класса дифференциальных уравнений, форма которых учитывала бы основное свойство реальных систем – их конечность во времени, а сами уравнения адекватно описывали бы начальное и (или) конечное состояние системы.

 Обратимся к качественному анализу динамики реальной эволюционирующей системы, например, живого организма. При рассмотрении динамики развития такой системы с необходимостью приходится вводить представление о двух связанных между собой понятиях времени: внешнем времени , которое описывает процессы взаимодействия с полем, и внутреннем времени , определяющем, в основном, внутреннюю динамику системы.       Динамика многих объектов, описываемая в рамках внешнего времени, является сугубо неоднородной. Обычно возможно чётко зафиксировать момент рождения и исчезновения живого организма. Так, например, в начальные периоды существования качественные изменения структуры биологических объектов в рамках внешнего времени  происходят во многих случаях очень быстро. Животное или растение в течение короткого промежутка внешнего времени проживает всю жизнь своих предков - внешнее время как бы сжимается по отношению к внутреннему. Затем, в зрелом возрасте, темпы изменения параметров динамики живого организма синхронизируются с темпами изменения окружающей среды. По мере старения организма темп изменения событий, определяемых внутренним временем, всё больше отстаёт от темпа изменения внешних событий, что, в конце концов, приводит к разрушению структуры. По иному происходит в ряде случаев процесс исчезновения структуры. Сначала возмущения накапливаются медленно, а затем темпы роста возмущений быстро нарастают, приводя к разрушению объекта.

    Проблема существования внутреннего времени живых систем, в частности Человека и Человечества, широко обсуждалась в работах физиков, биологов и философов. В монографии [1] приведён обзор некоторых работ, посвящённых этой проблеме.

    Основное предположение настоящей работы состоит в том, что динамика внутренних процессов в сложной системе, описанная в рамках внутреннего времени, не должна иметь ни начала, ни конца, то есть . Тогда во внутреннем  времени  динамика таких систем  должна описываться системой уравнений (1).

    Рассмотрим, как трансформируется такая система уравнений в случае перехода от внутреннего времени к внешнему. Введём функциональную связь между внутренним временем  и внешним временем :

 

.                                                  (2)

 

Тогда получим систему уравнений относительно внешнего времени

 

.                                            (3)

   

Предположим, что система (1) является автономной - оператор  не зависит от времени, то есть в рамках описания во внутреннем времени внешние условия, в первом приближении, не влияют на динамику системы. Множество значений вектора , являющихся решениями системы уравнений

 

,                                                 (4)

 

описывает совокупность стационарных состояний системы (1). Если вблизи стационарного состояния ввести некоторое возмущение, то поведение структуры во внутреннем времени может быть описано уже системой линейных дифференциальных уравнений для возмущённой части вектора .

    Решение системы уравнений

 

,                                              (5)

 

 где ,  стационарное состояние системы, а - линейный оператор, хорошо известно [2]. (В дальнейшем будем опускать значки над вектором и оператором). Если задаться начальным условием , то решение системы (5) имеет вид:

 

.                                                        (6)

 

В предположении о линейности оператора  можно выписать и решение системы уравнений (3)

 

.                                           (7)

 

    Проблема состоит в выборе преобразования (2), адекватно осуществляющего отображение внешнего времени на внутреннее, и в физической интерпретации решения (7).

    Целесообразно рассматривать, как минимум, два варианта.

1. Начальный период существования структуры во внешнем времени должен соответствовать лучу . Точка  должна отображаться в точку  - момент рождения структуры.

2. Конечный период существования структуры во внешнем времени должен соответствовать отрезку . Точка  должна отображаться в точку . - момент разрушения структуры.

    В качестве отображающих функций, обладающей этим свойством, могут быть выбраны логарифмические функции. Использование именно этих функций позволяет наиболее полно учесть особенности динамики живых организмов и самоорганизующихся систем, связанные с изменением темпов развития в различные периоды существования. Аналогичное предложение относительно связи физического и исторического времени сделано в [1] применительно к исследованию динамики человеческого общества.

 

1.                             ,                    (8)

 

2.                             ,  .               (9)

 

Здесь .- действительные числа.

    Рассмотрим подробно первый случай. Если система уравнений (1) автономна, то трансформированная система уравнений автономной уже не является и имеет вид:

 

                                              (10)

 

Если линеаризированная система (5) имеет аналитическое решение (6), то аналитическое решение системы (10) при может быть получено как результат подстановки в первое решение выражения (8).

 

,          (11)

 

где

                                       (12)

 

    Если в (11, 12) положить

 

           и ,

тогда

.

 

Если теперь принять дополнительно , то при значениях , близких к нулю, получаем .

Таким образом, класс линейных автономных систем асимптотически [3] является частным случаем рассматриваемого нами класса систем в экспоненциальном времени при специальном подборе коэффициентов отображения.

    Примем, что .  Тогда система уравнений (10) упростится

 

,                                           (13)

 

а её решение примет вид

 

.                          (14)

 

              Введём обозначение

.                                  (15)

 

              Тогда решение системы уравнений (14) примет вид

 

.                                     (16)

 

Обычно оператор  задан своей матрицей в некотором базисе. Требуется явно вычислить матрицу оператора  в том же базисе.

В настоящей работе рассмотрим только случай диагонального оператора, характеристическое уравнение которого

 

                                                   (17)

 

имеет различные корни. В собственном базисе, в котором матрица оператора  диагональна, она имеет вид:

 

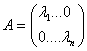,                                                   (18)

 

где  -собственные числа. Матрицы операторов  и  также имеют диагональную форму

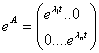                                                  (19)

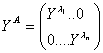                                                  (20)

Система уравнений (13) может быть решена, следуя [2], следующим образом:

1)                                                                                                                                                                                                                                                                         составить вековое или характеристическое уравнение

 ;

2)                                                                                                                                                                                                                                                                         найти его корни   (мы предполагаем, что они  различны);

3)                                                                                                                                                                                                                                                                         найти собственные векторы  из линейных уравнений

4)                                                                                                                                                                                                                                                                         разложить начальное условие, соответствующее в терминах экспоненциального времени , по собственным векторам

;

5)                                                                                                                                                                                                                                                                         написать ответ

.

 

    Отсюда следует важный вывод, являющийся обобщением результата [2.С.141]. Если оператор  диагонален, то элементы матрицы  в любом базисе являются линейными комбинациями степенных функций  , где -собственные числа матрицы .

В терминах собственных векторов и собственных чисел линейная задача с диагональной матрицей в терминах внешнего времени разбивается на  независимых комплексных линейных уравнений типа

 .                                                      (21)

Решение каждого из них имеет вид

 

.                                    (22)

                                                                                                    Если собственное число матрицы  действительно (), то могут быть рассмотрены следующие частные случаи поведения динамической системы вблизи особой (стационарной) точки в терминах внешнего времени.

1.  - в этом случае при стремлении  сверху значения зависимой переменной (параметра целого системы) стремятся к бесконечности тем быстрее, чем больше модуль величины . Физическая интерпретация динамики системы в данном случае может быть следующей. Можно считать, что выражение (22) лишь асимптотически описывает поведение системы при временах, больших, чем , а при  зависимая переменная получила значительное возмущённое значение .

                                                                                               Можно предположить также, что до момента  система находилась в области притяжения другого аттрактора, из которой она вышла по той или иной причине. При  приближение к стационарной точке происходит по степенному закону, то есть значительно слабее, чем по экспоненциальному закону во внутреннем линейном времени, тогда как вблизи точки  наоборот, затухание возмущения происходит значительно интенсивнее.

2. При  имеем постоянное значение .

3. - модель описывает степенную динамику роста переменной.

При этом можно выделить две зоны изменения параметра:

3а. , когда производная от  по  при  стремится к бесконечности, то есть происходит «ударное» возникновение системы с постепенным уменьшением производной до нуля при ;

3б. , когда производная от  по  при  стремится к нулю, то есть происходит «безударное» возникновение системы с постепенным увеличением производной до бесконечности при стремлении .

    Если =1, то зависимость обобщённой координаты от экспоненциального времени становится линейной.

                                                    Вблизи точки  характер изменения аналогичен характеру изменения вблизи точки . То есть поведение системы, описываемой уравнением (21), вблизи момента ,-который может быть назван моментом созревания, оказывается близким  к поведению породившей её системы во внутреннем времени, тогда как при удалении от этой точки как в сторону больших , так и в сторону значений , близких к , существенно отличается от неё, приобретая новые свойства.

В случае мнимого собственного числа  

 

.                           (23)

 

Полученное решение характеризует колебательный процесс с постоянной амплитудой и переменной частотой. Вычислим зависимость частоты процесса от времени. Преобразуем формулу (23) следующим образом. Введём время , то есть такой момент времени, в который мы вычисляем искомую частоту колебаний, и малый отрезок времени , характеризующий эту частоту. Тогда разлагая показатель экспоненты решения (23) в ряд Тейлора вблизи точки  по , получим

 

 .                             (24)

                                              

Второй сомножитель выражения (24) характеризует фазу колебаний в момент , а величина  характеризует мгновенную частоту колебаний в этот момент.

Если рассматривать значения , близкие к  , то частота колебаний растёт по гиперболическому закону и даже стремится к бесконечности в случае приближения к моменту рождения структуры.

Точка  является с точки зрения колебательных процессов , описываемых полученными уравнениями, границей раздела. При  мы можем выделить режим быстрых колебаний, частота которых убывает и стремится к   при . Затем она, замедляясь, падает до нуля. Это режим может быть назван режимом низкочастотных колебаний. Изменение частоты в функции от внешнего времени становится всё более слабым и может быть осуществлена синхронизация внутренних процессов в системе с внешними процессами в окружающей среде (поле).

    Если рассматривать комплексное значение , то происходит наложение закона изменения амплитуды колебаний, определяемой реальной частью коэффициента , на закон изменения частоты колебаний , определяемой его мнимой частью.

    Если рассмотреть случай, когда момент   является завершающим в жизни структуры, то получим подобные варианты, отличающееся тем, что график зависимости  симметричен относительно точки .

1. .  При стремлении  значения зависимой переменной асимптотически стремятся к бесконечности. Возникает режим, который был назван С.П. Курдюмовым [4 - 6] режимом с обострением. За конечный промежуток времени система стремится достигнуть бесконечного значения зависимой переменной. К такого типа режимам относилась до последних лет динамика роста человеческого общества, описываемая уравнением

,

что соответствует =-1 [1, 7-10].

                                                    В двух других режимах параметры системы либо гладко, либо ударным образом стремятся к стационарному состоянию, при этом как совершая, так и не совершая колебания. Такие режимы могут описывать либо стабилизацию некоторого стационарного состояния, либо плавное разрушение старой структуры. 

                                                    Комплексные степенные функции встречаются и в других задачах, например, при решении автономных дифференциальных уравнений со степенными функциями в правой части, а также в случае нелинейного комплексного дифференциального уравнения, в правой части которого стоит дробно-линейная функция от зависимой и независимой переменной [11].

              Анализ решения одномерного комплексного уравнения даёт ключ к решению многомерных задач, позволяющих исследовать динамику сложных систем. При этом возникает возможность также решать обратные задачи, по заданной реализации определять систему дифференциальных уравнений, которой удовлетворяет динамическая система, поведение которой исследуется экспериментально. Пример решения такой задачи приведён в работе [12].

 

Благодарность

Авторы благодарят Рэма Георгиевича Баранцева  за поддержку при написании настоящей статьи и новые идеи по дальнейшему развитию полученных в ней результатов.

 

Литература.

 

1. Капица С.П. Общая теория роста человечества: сколько людей жило, живёт и будет жить на Земле. М.: Наука. 1999. 190с.

2. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука. 1984. 272с.

3. Андрианов И.В., Баранцев Р.Г., Маневич Л.И. Асимптотическая математика и синергетика: путь к целостной простоте. М.: Едиториал УРСС. 2004. 304с.

4. Змитренко Н.В., Курдюмов С.П., Михайлов А.П. Теория режимов с обострением в сжимаемых средах. Сборник ВИНИТИ. Итоги науки и техники. «Современные проблемы математики. Новейшие достижения» М.: 1986(1987). Т. 28. С.3-99.

5. Режимы с обострением. Эволюция идеи: Законы коэволюции сложных структур. М.: Наука. 1998. 255с.

6. Управление риском. (Риск. Устойчивое развитие. Синергетика). М.: Наука 2000.431с.

7. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. М.: Наука. 1997.288с.

8. Подлазов А.В. Теоретическая демография. Модели роста народонаселения и глобального демографического перехода. Новое в синергетике: Взгляд в третье тысячелетие. М.: Наука 2002. С.324-345.

9. Басин М.А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Часть 1. СПб.: Норма. 2000. 168с.    

10. Басина Г.И., Басин М.А. Синергетика. Эволюция и ритмы человечества. СПб.: Норма. 2003. 260с.

11. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения. Изд. 2. М. Наука. 1986. 760с.

12. Басин М.А. O функции, описывающей поведение системы перед катастрофически.ми событиями, и дифференциальных уравнениях, которым она удовлетворяет. Письма в ЖТФ.2006.Том 32. Вып.8. Сс.30-33  

 

Конец формы

 

 

 

 

\

Этюд 14

 

САМООРГАНИЗАЦИЯ В РАСПРЕДЕЛЕНИИ МАСС ЭЛЕМЕНТАРНЫХ ЧАСТИЦ.

 

 

   Одной из не решённых до настоящего времени проблем является теоретическое предсказание масс элементарных частиц. В большинстве существующих теорий массы частиц считаются заданными, то есть взятыми из эксперимента или получившимися из масс других частиц при взаимодействии с учётом выполнения закона сохранения энергии [1]. Поэтому любая новая попытка построить теоретически шкалу масс элементарных частиц имеет право на существование.

   С нашей точки зрения такая шкала должна удовлетворять следующим условиям:

- она должна быть максимально простой;

- она должна зависеть от одного единственного параметра и все фундаментальные массы должны быть простыми, но нелинейными функциями от этого параметра;

- она должна обладать определённой предсказательной силой.

   Основой предлагаемой ниже шкалы является допущение о том, что в природе существуют пра - частицы, формирующие структуру Вселенной, закон распределения масс которых прост, а все более сложные частицы, в том числе и те, которые мы называем элементарными, обладают массами, значения которых резонансно [2], [3], [4] концентрируются около той сетки, которая задана массами пра – частиц.

   Считаем, что все пра-частицы обладают некоторой положительной массой, при этом минимальной массой обладает пра-частица, резонансная гравитону (пра-гравитон). Далее примем, что фундаментальными на этом уровне рассмотрения является не суммы и разности, а отношения и степени масс [5]. В работе [6] представлена математическая модель, анализ которой показывает, что в области комплексного переменного резонансными свойствами, приводящими к самоорганизации, обладают значения зависимой переменной, соответствующие рациональным значениям степени, в которую возводится некоторый параметр, а наиболее сильные резонансы наблюдаются при обратных целым значениях показателей степени  , чем меньше число  , тем сильнее резонанс.

   Если эту модель применить к поставленной нами проблеме, то естественным становится предположение, что должна существовать фундаментальная пра - частица, к массе которой должны относиться массы всех пра - частиц.  На эту роль подходит пра - частица, имеющая массу, равную Планковской массе.

 .                                  (1)

   Теперь необходимо подобрать масштаб шкалы, то есть безразмерный параметр, характеризующий отношение Планковской массы к массе пра-гравитона

  .                                                           (2)

   В качестве дополнительной опорной точки выберем массу стабильной частицы, масса которой определена достаточно точно и которая может считаться в настоящее время наиболее простой. Основным кандидатом на такой выбор является электрон.

   Будем считать, что при нелинейном резонансном взаимодействии сетки пра-частиц и электрона происходит самоорганизация, в результате которой масса электрона принимает значение, близкое к массе одной из стабильных пра - частиц.

Масса покоя электрона -  [1].

Отношение Планковской массы к массе электрона

  .                              (3)

Далее примем, в соответствии с упомянутой математической моделью, что

 .                                                   (4)

Отсюда определим

                                                (5)

   Полученная величина не может считаться точной, так как мы приняли несколько допущений, которые могут уточняться в процессе дальнейших построений и сопоставления с экспериментальными данными.

   Наше следующее допущение, вытекающее из той же модели, состоит в том, что отношения масс всех основных пра - частиц к Планковской массе должны лежать на шкале, элементы которой являются обратными корням целой степени   из  . Это допущение позволяет построить следующую таблицу:

 

                                                                                              Эксперимент [1]

n =1. Масса пра-гравитона.  . .

n =2. Масса пра-фотона.      .   .

 .

n =3.Масса пра-глюона .

n =4.Масса пра-нейтрино.   .   .

                                                                                 .

n=5.Масса пра-электрона.  .  .

                                                                                    

n =6. Масса пра-бариона.     .  .

               Масса протона  

n =7. Масса Пра-ВКБ  .      .

                                           .

                                                                             .

 

   Построенная сетка не может считаться окончательной и её параметры должны быть уточнены путём дополнительных теоретических построений и привлечения других экспериментальных данных. Однако, качественное совпадение порядков параметров сетки и соответствующих им масс стабильных частиц не может быть случайным и говорит о возможности применения разработанной математической модели к построению приближённой шкалы масс элементарных частиц.

         Интересно рассмотреть связь введённой нами новой мировой константы с одним из чисел Абрама Моисеевича Басина[7]

 

1. Физические величины: Справочник/ А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др. Под ред. И. С. Григорьева, Е. З. Мейлихова. М.: Энергоатомиздат. 1991.1232 с.

2. Басин А. М. Качка судов. (Учебник). М.: Транспорт.1969. 272 с.

3. Басин М. А. Вихре - волновой резонанс в гидродинамике подводного крыла. Международный симпозиум по гидродинамике судна, посвящённого 85 летию со дня рождения Абрама Моисеевича Басина. Материалы симпозиума. Под ред. М. А. Басина. СПб.: Изд. СПбГУВК 1995. С.399-407..  

4. Басина Г. И. Басин М. А. Синергетика. Вселенная резонансов. СПб.: Норма. 2008. 144с.

5. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб.: Норма. 2002.144 с.

6. Басина Г. И., Басин М. А. Комплексные математические модели. Тезисы доклада, представленного на XVI Международную конференцию: «Математика. Экономика. Образование». Дюрсо: 27 мая - 3 июня 2008 г.

7. Басина Г.И., Басин М.А. Синргетика. От чисел Басина до Synergonet. Публикация в Internet

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ъ

 

Этюд 15.

Триады в Синергетике.

 

.

 

80 –летию Рэма Георгиевича Баранцева посвящается

.

    Одним из базовых элементов синергетической методологии  является тринитарный подход к исследованию целостных объектов природы, интенсивно разрабатываемый Р.Г. Баранцевым [1-6 ].

Вот что он пишет [3. Сс. 26-28.]:

”…диада, или бинарная оппозиция, есть элементарная структура анализа. Синтеза на ней не построить. Для синтеза требуется более ёмкая структура. Примеры из естественных наук подсказывают, что следует обратиться, по меньшей мере, к триадам…

…          Будем называть триадой совокупность из трёх элементов, каким-то образом связанных между собой. В зависимости от вида связи различаются следующие типы триад.

Линейные (вырожденные, одномерные), когда все три элемента расположены на одной оси в семантическом пространстве. Например, 1-10-100, дивергенция-параллелизм-конвергенция, левые – центр - правые. Структурно они не богаче, чем диады.

Переходные (гегелевские), характеризуемые известной  формулой «тезис-антитезис-синтез». Они лишь провозглашают снятие противоречия, не раскрывая его движущей структуры.

Системные (целостные), единство которых создаётся тремя элементами одного уровня, каждый из которых может служить мерой совмещения двух других. Все три принципиально равноправны.

    Особого внимания заслуживает общее семантическое свойство всех системных триад, сложившихся в самых разных культурных традициях... 

    Источник этой закономерности можно видеть в способности человека мыслить одновременно и понятиями, и образами, и символами.

Предлагаемая  семантическая формула системной триады

 

                                                Интуицио

                                                  /           \

                                          Рацио ------- Эмоцио

 

использует понятия, сложившиеся в диадной парадигме, и потому довольно условные. Новое смысловое содержание должно постепенно наполняться по мере их проявления в такой триадической структуре. Перекодировка понятий составляет значительную трудность при любой смене парадигмы. Стереотипы, закреплённые в подсознании, очень трудно вытащить и преодолеть на уровне сознания. Тут не обойтись без «эмоцио» и «интуицио»”.

    Фундаментальная системная триада может рассматриваться как основа процесса познания. Её отображение на модели сложных самоорганизующихся систем и отыскание её аналогов в природе и обществе является мощным орудием познания окружающего мира.

    В настоящей статье мы приведём несколько примеров использования тринитарной методологии в синергетических исследованиях.

    При мысленном выделении объекта из природы мы создаём в мозгу его образ, называем его каким-либо именем и можем ввести некоторые числа, например, единицу и нуль, характеризующие существование и отсутствие объекта.

    Таким образом, формируется первичная триада форм представления результатов познания

 

Слово

/        \

Число ---Образ.

 

    Создание в мозгу образа изучаемого предмета соответствует эмоциональному элементу фундаментальной триады. Это первый уровень абстракции.

    Название объекта, базирующееся на сравнении ряда близких образов, может считаться проекцией интуитивной компоненты фундаментальной триады. Слово обычно обозначает некоторый класс предметов или событий.

    Введение чисел позволяет включить в анализ строгие методы логических и математических рассуждений, то есть «рацио».   

    Определение первичной триады позволяет ввести в рассмотрение три языка синергетики (эти языки одновременно являются языками познания)

 

            Язык слов

          /           \

Язык математики-------- Язык образов

 

формирующих ещё одну системную триаду.

    Получая информацию об окружающем мире из внешней среды при помощи органов чувств, а также используя переданную нам по наследству генетическую информацию, мы выделяем, основываясь на ней, отдельные объекты и явления, создаём в мозгу визуальные, звуковые, обонятельные, вкусовые, тактильные образы, устанавливаем их связь с определёнными объектами и явлениями окружающего мира. Этот сложный процесс вовсе не всегда является однозначным. Одна и та же информация может восприниматься одним и тем же индивидуумом в различное время или различными людьми по-разному – её восприятие может порождать различные образы. Процесс распознавания образов – бифуркационный процесс. Это многократно показано в ряде произведений искусства, литературных произведений, а также в научных исследованиях [7-10].

    Чтобы выжить в окружающем мире и адекватно реагировать на изменяющуюся обстановку человек (а возможно, и высшие животные) должны уметь классифицировать объекты и явления окружающей среды, а следовательно, и их образы, выделять среди них полезные и опасные для жизни. Они должны сообщать своим сородичам об опасных и благоприятных для их жизни условиях. Для человека формой такого общения явился язык слов, позволяющий назвать одним словом целый класс образов различных объектов, имеющих сходные признаки, или осознать в качестве одного объекта его образы, полученные в результате обработки информации об этом объекте, полученные в различные моменты времени. Слово – звуковой символ, характеризующий объект (квант) или класс объектов (обобщённую волну), и позволяющий передавать информацию от одного человека другому. Наряду со словами, выражающими те или иные предметы, в языке присутствуют слова, характеризующие движение, действие, место, качество, желание и т.д. Язык слов формировался в течение тысячелетий в виде живой самоорганизующейся системы, отражающей процесс познания человеком окружающего мира и являющейся одним из главнейших орудий общения внутри человечества. Развитие языка происходило одновременно с ростом информации, получаемой людьми из окружающего мира. Язык слов, произносимых и слышимых, а также выраженных в виде совокупности знаков – письма, является не только и не столько языком науки, но и всех форм познания окружающего мира, языком искусства и философии (религии). В связи со сделанным замечанием следует упомянуть ещё одну известную триаду познания окружающего мира

 

                                  Философия (Религия)

                                          /                   \      

                                Наука------------Искусство

 

Каждая из включённых в эту триаду форм познания окружающего мира использует в определённой мере все три языка: образный, словесный и символьный (язык математики), однако уровень их использования различен. Поэтому можно установить сферы притяжения между формой изучения окружающей среды и языком, наиболее адекватно соответствующим той или иной области знания.

Науке наиболее соответствует язык математики.

Искусству – язык образов

Философии и религии – язык слов.

Однако, это соответствие не абсолютно. Язык слов, например, стал одним из важнейших языков искусства. И здесь, в рамках искусства, сформировалась новая триада

                                                Художественная

Литература

/                       \

Изобразительное-------- Музыкальное    ,

Искусство                    Искусство

 

элементы которой всё больше проникают друг в друга .

    Остановимся более подробно на языке математики; языке символов и чисел и действий над ними. В математическом языке и в самой математике можно выделить свои триады [11].

 

 

 

    Например:

Аксиома

/         \

         Теорема-----Определение

 

Аксиома - истина, не требующая доказательства, её формулировка является результатом опыта, приобретённого человечеством за время его существования («интуицио»).

Определение – индивидуально, может иметь эмоциональную окраску. Разные учёные и различные математические школы могут давать различные определения.

Теорема – цепочка логических рассуждений (рацио).

Эта триада составляет основу языка математики.

    Однако, при анализе самой математики как системы целесообразно ввести другую триаду

 

Континуальность

/                             \

Иерархия--------------- Размерность

 

    Понятие континуальности является в математике сравнительно новым и связано с развитием теории множеств. Мощность конечного множества определяется числом его элементов. Переход к счётным бесконечным множествам осуществляется за счёт абстрактного логического построения. На вопрос, есть ли в природе какой либо аналог счётного множества ответа пока нет. Переход к следующему классу, – континуальных множеств, - осуществляется путём рассмотрения всех возможных подмножеств счётного множества. Таким же путём можно логически строить бесконечные множества любой мощности.

    Другой координатой триады является размерность. На примитивном уровне размерность характеризует число неизвестных, описывающих изучаемый процесс. Для континуальных множеств размерность приобретает особое значение, так как позволяет вводить независимые координаты и строить на их основе дифференциальную геометрию, являющуюся базисом классической математики и современной физики.

Однако, живая природа, по-видимому, описывается другой геометрией. Здесь необходимы обобщения и одним из таких обобщений является фрактальная геометрия, позволяющая вводить значения размерности, включающие любые действительные числа [12-14, 3].

    Наконец, третьим элементом рассматриваемой триады является иерархия, характеризующая степень нелинейности рассматриваемых математических проблем [11].

    К первому уровню иерархии относится широко представленный в классической математике класс линейных проблем.

    Второй уровень характеризуется степенными многочленами. В последние годы возникла и сейчас интенсивно развивается «степенная математика»´[15, 16]

    Переход от первого уровня ко второму может быть осуществлён за счёт введения обобщённых экспоненциальных отображений.

    Попытки перейти со второго уровня иерархии на третий приводят к появлению многозначных функций, графов, сетей, фрактальных множеств и других необычных математических объектов. Некоторые из них исследуются при помощи введения случайных переменных и процессов. Именно на этом уровне проявляются нерешённые проблемы современной математики. Можно предположить, что именно на этом уровне должна описываться динамика живых систем.

    При исследовании проблем этого уровня математики и соответствующего ему уровня структур и явлений природы тринитарный метод может оказаться особенно эффективным.

    Качественный анализ нелинейных волн, структур и транспортно- информационных систем, выполняемый нами в настоящее время, [10, 11, 17-21] показывает, что рассматриваемые классы могут быть объединены в системные триады. Основная из них имеет вид.

 

Грибовидные

структуры

/                    \

Нелинейные------------- Транспортно-

волны                       информационные

                                системы

 

Материальной базой классификации может служить понятие нелинейной волны, сохраняющей свои свойства при движении относительно внешней среды. Нелинейная трансформация волн при росте степени нелинейности приводит после нескольких шагов бифуркаций к формированию грибовидных структур, приобретающих различные формы и мультипольно воздействующих на окружающую среду. Эти структуры обладают возможностями самодвижения и их бифуркации во многих случаях приводят к усложнению структуры и появлению у неё новых свойств, некоторые из которых оказываются достаточно устойчивыми.

    Эмоциональный аспект в данной триаде мы приписываем транспортно- информационным системам, являющимся во многих случаях результатом взаимодействия нелинейных волн и грибовидных структур. В некоторых случаях сами транспортно-информационные системы могут рассматриваться как грибовидные структуры или нелинейные волны.

    Элементы рассматриваемой триады тесно связаны между собой через  переходные структуры, являющиеся результатом бифуркации элементов основной триады.  Нелинейные волны порождают в сплошной среде зоны скачков параметров – замкнутые границы, формирующие объекты, названные нами  телами-волнами. А нелинейные перемещения самих границ в сочетании с формированием на них новых разрывов порождают промежуточные вихревые структуры, являющиеся основными элементами грибовидных (мультипольных) структур. Множественные бифуркации границ порождают также  структуры, названные нами древовидными, так как их математическое моделирование может быть осуществлено с помощью теории графов. Нелинейное взаимодействие грибовидных и древовидных структур порождает наиболее сложные транспортно информационные системы.

Таким образом, наряду с основной триадой формируется переходная –

 

Вихревые-------- Древовидные

Структуры        Структуры

\          /

  Тела

Волны

Их объединение порождает комплексную совокупность триад

                                                     Грибовидные

                                                       структуры

                                                     /                  \     

                                Вихревые--/----------------   \  Древовидные

                            Структуры/ \                      /\Структуры

                                                   \                    /   \

                            Нелинейные --\---------------/---  \--Транспортно-

                                  волны           \              /        информационные

                                                         \          /            системы

                                                     Тела-Волны

 

    Обычно любая система расположена в некоторой среде – поле.

Анализ этого свойства природы приводит к введению новой триады

 

 

 

                                                               Поле

                                                              /       \

                                                    Квант-----Обобщённая

                                                                      Волна

 

Всякая структура или система является элементом (квантом) некоторого класса идентичных структур или систем (обобщённой волны). Как отдельная структура, так и совокупность близких (или идентичных) структур взаимодействуют с окружающей средой – полем.

    Триадная методология исследования использована нами при исследовании одного из элементов построенного ранее комплекса - транспортно- информационных систем [10].

    Основным свойством транспортно-информационных систем, является то, что они состоят из большого количества  взаимодействующих между собою элементов, каждый из которых участвует в локальных бифуркационных  процессах, то есть процессах, которые включают в себя события, которые могут иметь конечное или бесконечное число возможных исходов. Поэтому поведение, а следовательно и его знаковое описание, для таких систем не может быть строго детерминированным.

 В транспортно-информационных системах, элементы которых и они сами участвуют в бифуркационных событиях, возникает необходимость в появлении специального внутреннего механизма выбора.

По-видимому, именно возникновение и совершенствование этого механизма, названного нами управляющей системой – контроллером,- в транспортно-информационных системах волнового типа является основным механизмом эволюционного развития.

Включение в рассмотрение контроллера позволило построить фундаментальную триаду элементов взаимодействия, включающую  в себя

а) материальную часть системы взаимодействующих структур,

б) поле, взаимодействующее с системой,

в) контроллер системы.

    Диада структура - поле дополнена до целостной триады новым элементом – контроллером.

    В зависимости от соотношения элементов этой триады внутри класса, охватывающего все сложные системы, в том числе и самоорганизующиеся, могут быть выделены подклассы, различающиеся особенностями  процессов, в которых участвуют входящие в них системы, а также структурой элементов триады.

а) Системы квазидетерминированного типа, бифуркационные процессы внутри которых оказывают незначительное влияние на их макропараметры.

      Основным свойством таких систем является значительная разница между масштабами самой системы как обобщённой волны и отдельными элементами (квантами), её составляющими, а также близость параметров квантов. Для них характерны экспоненциальные законы статистических распределений параметров

    Границы таких систем, являющиеся обычно волновыми структурами, во многом определяют их макроскопические свойства. Для изучения этих свойств существуют глубоко разработанные методы равновесной и неравновесной статистической физики и механики сплошных сред.

    При этом квази - детерминированность на системном (обобщённо - волновом) уровне допускает различные уровни хаотичности на уровне квантов. Большинство макроскопических объектов неживой природы относится к этому подклассу.

 

б) Транспортно-информационные системы, у которых реализуется иерархическая материальная и информационная связь между уровнем системы-волны и элемента-кванта.

 

В таких системах обычно выстраивается масштабная иерархия подсистем. Эта масштабная иерархия может иметь квази-фрактальный характер. Именно в таких системах наблюдается соответствующее их квази-фрактальной структуре степенное статистическое распределение масштабов элементов и подструктур.

На каждом уровне иерархии такой системы её подструктуры проявляют свою свободу.

 

в) Транспортно-информационные системы, способные к размножению, то есть к формированию себе подобных систем.

 

    Способность к размножению не является прерогативой только транспортно-информационных систем. Практически в той или иной степени это свойство характерно для любых  колебательных и волновых систем, начиная от линейных колебаний и волн. Однако, когда мы переходим к рассмотрению транспортно-информационных систем третьего подкласса, то их размножение может иметь специфический характер, проявляя, особенно у живых систем, такую сложность, которую невозможно даже помыслить у структур более простых типов. Здесь возникают структурно-волновые резонансы и  могут появляться логарифмические законы распределения параметров элементов.

    г) Транспортно-информационные системы, способные моделировать свою динамику и динамику окружающей среды-поля и выбирать близкие к оптимальным модели бифуркационного поведения.

 

 Именно у таких систем интенсивно развивается, определяя их эволюцию, внутренний контроллер, названный нами гомеостатическим.

 

д) Транспортно-информационные системы, обладающие сознанием и творческими способностями.

 

Системе, участвующей в бифуркационных событиях, мы сопоставили целостную триаду [22]

Поле

(Ближнее и Дальнее)

/                     \

Структура --------------Контроллер

(Основная часть системы)      (Управляющая система)

 

.

    Структура (внешняя материальная часть системы) – это часть объекта, которая взаимодействует с полем на материальном и энергетическом уровне,

     Поле (ближнее и дальнее) – это внешняя по отношению к структуре совокупность объектов, интенсивно взаимодействующих со структурой. Поле может быть условно разделено на ближнее и дальнее, для исследования взаимодействия которых с системой могут быть применены асимптотические методы [4].

    Контроллер (управляющий механизм) – внутренний механизм системы, обеспечивающий выбор из числа возможных исходов бифуркационного события или процесса того, который приведет к наиболее устойчивому  состоянию системы.

Появление контроллера включает в действие механизм эволюции. Развиваются в непосредственной связи между собой все три элемента триады. Возникает тройное резонансное взаимодействие (по-видимому, здесь действует механизм структурно-волнового резонанса [11]), приводящее к  увеличению сложности и динамической устойчивости (увеличению числа возможных исходов бифуркацонных событий и увеличению информации, хранимой и перерабатываемой контроллером).

Анализ триады сложной волновой транспортно-информационной системы показывает, что все её элементы могут быть изучены более глубоко и для каждого из них может быть построена своя внутренняя системная триада.

Структура характеризуется тремя главными координатами: мерой, типом и иерархией.

                                 

                                                           Тип

Структура                                        /      \

                                                   Мера-----Иерархия

 

    Мера -характеризует величину основного параметра структуры, который часто (но далеко не всегда) совпадает с параметром целого всей системы.[10-11]

Тип - Структура может быть отнесена к одному из классов волн, вихревых, грибовидных и древовидных структур или транспортно-информационных систем, в соответствии с построенным выше комплексом. Относя структуру к определенному классу, мы определяем тип структуры.

Иерархия - Сложные системы обычно состоят из подсистем различных масштабов, связанных между собой. Каждая из них может иметь свою меру или свой тип. Вместе они образуют иерархию сложной системы.

 

Аналогичная триада формируется  в управляющем механизме.

 

 

                                                                 Информация

Контроллер                                              /                  \

                                                     Управление ----------Память

 

Управление. - Главная «цель» управляющего механизма - это управление вероятностями исходов бифуркационных событий. Управление производится путём изменения иерархической структуры объекта, установления новых внутренних связей, а также активации, разрушения или резервирования старых.

Информация. - Для такого управления необходимо получение информации об изменениях, происходящих в самой системе и во внешнем поле.

Память -  специальный механизм сохранения и переработки полученной ранее информации, а также своевременного использования её для целей управления.

Контроллер – это механизм управления бифуркационными процессами, в которых участвует система. Контроллеры могут быть двух типов.

1. Контроллер, порождающий структуру.

2. Контроллер, обеспечивающий устойчивое существование структуры, выбор ее поведения при взаимодействии с полем, способный до начала событий изменять вероятности реализации возможных результатов, а также осуществляющий в момент события выбор того или иного конкретного результата - гомеостатический контроллер.

 

1.Контроллер, порождающий структуру,

 

Он может находиться как вне структуры, в её поле, так и внутри самой структуры. Порождающий контроллер должен обеспечивать  существование и воспроизводство обобщённой волны, в которую структура входит как квант.

 

Гомеостатический контроллер.

 

 В результате формирования системы и выхода её на режим стабильного существования возникает стационарный режим обмена веществом, энергией и информацией между структурой и полем, при котором параметр целого системы остаётся близким к постоянной величине. Устойчивость этого режима и безопасность системы обеспечивает гомеостатический контроллер.

     Основной принцип его действия – это обобщённый принцип обратной связи. Он реализуется через управление вероятностями исходов бифуркационых событий и процессов. Любое возмущение внешнего поля приводит к возмущению параметров системы. При этом включается нелинейный механизм стабилизации, возвращающий гомеостаз.

Пусть произошло некое событие, связанное с локальным взаимодействием структуры и поля, в результате которого структура изменила свое состояние. Тогда гомеостатический контроллер в соответствии  с памятью об аналогичных процессах, которые происходили со структурой ранее, разрабатывает и реализует модель поведения, целью которой является приведение системы после воздействия флуктуации в состояние, максимально близкое к равновесному. С этой целью обмен веществ и энергии изменяется таким образом, чтобы обеспечить такую серию бифуркационных событий, чтобы она привела к гомеостатическому состоянию, или близкому к нему. Одновременно происходит и совершенствование системы управления. Она запоминает порядок действий, все успехи и неудачи в достижении цели, и в следующий раз приходит к цели более эффективным способом.

Поэтому одним из главных орудий гомеостатического контроллера является накопление информации о возможных способах решения поставленной задачи, полученной в результате свершения бифуркационных событий и процессов - память о прошлом.

Основным свойством гомеостатического контроллера является также способность моделирования будущего, исходя из поставленной цели и информации, накопленной в прошлом. Здесь возникает проблема получения контроллером знания, то есть информации о возможном будущем.

 

Поле – это внешняя среда, окружающая структуру. Для континуального описания, наиболее удобного для поля, используются системы непрерывных обобщенных координат, число которых может быть как конечным, так и бесконечным. В рамках континуального подхода поле описывается потенциалами различных типов. Кроме того, поле несёт информацию о происходящих в нём событиях. Таким образом, поле также может охарактеризоваться триадой.

 

        

 

 

 

                                                   Координаты.

                                                      /                   \

                                        Потенциал( тип)---Информация

 

Координаты – параметры пространства (обычно непрерывного и многомерного), в котором происходят те или иные события.

Потенциал (тип) – определяет характер взаимодействия поля со структурами или системами.

Информация  - данные о бифуркационных процессах, происходивших с объектами, взаимодействующими с полем и между собой.   

    Выстроенные триады могут быть объединены в единый комплекс .

 

 

                                                         Координаты             

                                                              /              \

                                        Тип  потенциала        Информация

                                       Тип структуры           Информация-

                                           /                \                 /                      \

                                     Мера -----Иерархия -Управление ---- Память

                                                                             

Соответствующие элементы триад взаимодействуют между собой, но у каждой триады есть свой особый элемент, не соединяющий ее с другими. Эти особые элементы вновь формируют триаду

 

 

                                                     Координаты

                                                         /          \

                                                    Мера------- Память

 

Между элементами этой узловой триады может быть построена новая триада

 

                                                  Материя --Творчество

                                                              \           /

.,                                                       Управление

 

Объединение первого и последнего  треугольников характеризует основные параметры сложной –транспортно- информационной системы

 

.                                                        Поле       

                                                         /         \

                                       Материя /           \    Творчество

                                                   Х               Х

                                  Структура --\--------/-- Контроллер

                                                         \       /

                                                   Управление

 

Выполненный выше тринитарный анализ сложной транспортно-информационной системы был с успехом использован при исследовании таких систем как Человечество и  Internet [10,.23- 26] 

Так как возникновение и эволюция контроллера является принципиально новым фактором, отличающим сложные транспортно-информационные системы, то причины его появления и механизм действия требуют специального рассмотрения и анализа. Если бы все события в природе были детерминированы, и процессы происходящие со всеми структурами были заранее предопределены, то никакой потребности в контроллере бы не возникло. Информация и представление о ней возникают только как следствие  существования неопределённости, при совершении бифуркационных событий.

Однако, это только одна сторона информационного процесса. Возможность существования в природе бифуркационных событий и процессов порождает принципиальную неполную предсказуемость будущего, а следовательно, возможность управления будущим, путём выбора одного из возможных исходов. В этом случае  возникает необходимость предсказания будущего - знания. Переход от информации о прошлом к информации о будущем - знанию – это творческий процесс. Резкий скачок информации о будущем может произойти без дополнительного получения информации о прошлом и наоборот, можно получать бесконечное количество информации о прошлом, не выжимая из неё информации о будущем.

При изучении систем, управляемых контроллером, необходимо не только анализировать динамику её основной материальной структуры и строить соответствующие  математические модели,  но также и знать принципы действия контроллера и моделировать процесс создания им моделей поведения. Здесь возникает новая триада.

 

                                        Исследователь

                                          /                     \

                              Структура-------Контроллер

 

Синергетика приходит к необходимости исследования закономерностей динамики моделей – динамики знаковых систем – семиодинамики [6].

 

 

 

 

Литература.

 

1. Баранцев Р. Г. Нелинейность – когерентность - открытость как системная триада синергетики // Мост. 1999. №29. Сс. 54-55.   

2. Баранцев Р. Г. Имманентные проблемы синергетики // Вопросы философии. 2002. № 9. Сс.91-101.

3. Баранцев Р.Г. Синергетика в современном естествознании. М.: Едиториал УРСС. 2003. 144c.

4. Андрианов И. В. Баранцев Р. Г., Маневич Л. И. Асимптотическая математика и синергетика: путь к целостной простоте. М.: Едиториал УРСС. 2004. 304 с.

5. Баранцев Р.Г. Становление тринитарного мышления» М.-Ижевск: НИЦ «Регулярная и хаотическая механика». 2005. 124с.

6. Баранцев Р.Г. «История семиодинамики: документы, беседы, комментарии». М.-Ижевск: НИЦ «Регулярная и хаотическая механика». 2006. 376с.

7. Хакен Г. Синергетика. М: Мир.1980. 414с.

8. Хакен Г. Синергетика. Иерархия неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир 1985.

9. Хакен Г. Информация и самоорганизация М. «Мир» 1985 (4-й том в Шпрингеровской серии книг по синергетике http://link.springer.de/ol/total/sist.htm

10. Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. СПб.: Норма. 2003. 260с.

11. Басин М.А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. СПб.: 2002. Норма 144с.

12.Feigenbaum M. J. Quantitative Universality for a Class of Nonlinear Transformations , J. Stat. Phys.,1987.V. 19.№1. Pp.25-52

Фейгенбаум М. Универсальность в поведении нелинейных систем. УФН.1983. Т.141.В.2. Сс.343-374.

13. Mandelbrot B. Fractals: Form, Chance and Dimension. San Francisco: Freeman Comp. 1977. 365p.

14. Mandelbrot B. Fractals. Paris: Hazard et Finance, Flammarion.. 1997

15. Брюно А. Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: Наука. Физматгиз. 1998. 288с.

16. Брюно А. Д. Самоподобные решения и степенная геометрия// УМН 2000. Т. 55. № 1

17. Басин М.А. Синергетика. Волновой подход к исследованию открытых структур и систем // Проблемы ноосферы и устойчивого развития. Материалы первой международной конференции. СПб. 9-15 сентября 1996 года. СПб.: Изд-во СПбГУ. 1996

18. Басин М.А. Основы классификации нелинейных волновых движений,

вихрей и транспортных систем // Синергетика и методы науки. СПб.: Наука.

1998. Сс.356-375.

19. Басин М.А. Волны. Кванты. События. Волновая теория взаимодействия структур  и систем. Часть 1. СПб.: "Норма".2000. 168с.

20. Басин М.А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно-информационные системы // Международная междисциплинарная научно-практическая конференция : «Современные проблемы науки и образования» . Керчь 27.06.-4.07.2001 г.Ч.1. Харьков.2001.Сс.12-13.

21.Басин М.А. Информационно-волновая теория структур и систем.// Материалы Второй научной конференции Санкт- Петербургского союза учёных: "Проблемы  и перспективы междисциплинарных фундаментальных исследований". 10-12 апреля 2002  года СПб.2002.C.8-9.

22. Басина Г. И., Басин М.А. Синергетика. Основы методологии. СПб.: Норма (в печати)

23. Басин М.А., Шилович И.И. Синергетика и Internet (Путь к Synergonet) СПб.: Наука. 1999. 71с.

24. Басин М. А., Шилович И. И.  Путь в Synergonet. СПб.: Норма 2004. 128 с.

25. Басин М.А., Шилович И.И.  Путь в Synergonet//"Современные проблемы науки и образования". Материалы международной конференции Керчь, 27 июня-4 июля 2001 года. Харьков: 2001.Часть 1.Cс.177-178

26. Басин М.А. Шилович И.И. Синергетика и Internet. Путь в Synergonet.// Материалы Второй научной конференции Санкт-Петербургского союза учёных: "Проблемы и перспективы междисциплинарных фундаментальных

исследований". 10-12 апреля 2002 года СПб.2002.C.10.

 

 

 

 

 

 

 

 

 

 

 

 

                                                     Этюд 16

                     

                     Основная  триада человеческого общества

 

Основные элементы синергетической парадигмы; рассмотренные Р. Г. Баранцевым, также формируют целостную триаду, определяющую свойства систем, изучаемых Синергетикой [2], которые одновременно являются свойствами самой Синергетики и областями сращивания её с основными элементами триады научного знания.

                                                            Открытость

                                                             /              \

                                              Нелинейность----Когерентность

 

При мысленном выделении объекта из природы мы составляем в мозгу его образ, даём ему имя и вводим в рассмотрение два числа: единица и нуль, - характеризующие соответственно существование и отсутствие объекта. Тем самым, мы вводим в рассмотрение три языка Синергетики и науки вообще:

 

                                                       Язык слов.

                                                         /         \

                                 Язык математики ----Язык образов,

 

Эта триада также соответствует семантической целостной триаде Р. Г. Баранцева [1-5]:

Синергетика внесла в использование этих языков специфические особенности и новые связи. Достижения качественной теории динамических систем и нелинейных волн, структур и систем, изучение диссипативных систем, внедрение тринитарной методологии и мягких математических методов асимптотической математики, создание основ информационно-волновой теории структур и систем привели к появлению новых мысленных и графических образов, новых слов и определений, новых математических понятий, которые благодаря синергетическим исследованиям внедряются во все элементы основной триады научных дисциплин.

В рассмотренные выше целостные триады в качестве «рацио» входит математика со своим специфическим языком. В свою очередь в математике можно ввести следующую целостную триаду, позволяющую по-новому взглянуть на её структуру как объекта синергетических исследований:

 

                                         Континуальность (мощность)

                                                   /                            \

Размерность (число переменных)-----Иерархия (степень нелинейности)

 

Рассмотрим первоначально движение по оси континуальности.

В начале этой оси можно расположить числа 0 и 1. Следующими по этой шкале располагаются конечные множества (которые могут быть взаимно однозначно отображены на конечную совокупность целых чисел). Далее по шкале континуальности расположены счётные бесконечные множества (натуральный ряд чисел, бесконечные последовательности, совокупность рациональных чисел и т .д.). Далее располагаются множества, обладающие мощностью континуума (иррациональные числа, действительные числа, комплексные числа, конечномерные матрицы и т.д.). Дальнейшее продолжение шкалы лежит в области определения мощности совокупности подмножеств множества континуума и т. д.[10].

Аналогичным образом можно перемещаться по оси размерности. Размерность –понятие, характеризующее число одновременно рассматриваемых переменных. Величина размерности может пробегать ту же совокупность значений, что и величина континуальности – от нуля и единицы до континуального множества координат, а, возможно, и далее.

Анализ иерархической координаты математики начнём с линейных отображений. Линейная функция может быть определена на любой точке плоскости, формируемой двумя первыми координатами: мощностью и размерностью. Однако уже анализ цепочек линейных отображений выводит на следующий уровень иерархии.

Цепочка линейных отображений, определяемых заданной функцией, порождает некоторый процесс, являющийся моделью потенциально бесконечной структуры. Эта последовательность порождает новый, сначала дискретный (принимающий последовательно целые значения) параметр времени, который при помощи предположения о гладкости рассматриваемых функций может быть преобразован в континуальный параметр. На этом уровне иерархии в математике появляются системы линейных дифференциальных уравнений, решениями которых оказываются экспоненциальные отображения. Этот процесс, с теми или иными особенностями, может быть осуществлён над всей плоскостью континуальность-размерность и именно его изучению посвящена большая часть математических исследований.

Второй этаж иерархии формируется из первого путём взятия обобщённых экспонент от линейных операторов, действующих на первом этаже. Аналогично, переход от второго этажа к первому можно рассматривать как обобщённое логарифмирование функций и операторов, действующих на втором этаже.

В последнее время интенсивно ведутся исследования в области перехода со второго этажа на третий, где многозначность функций, графы, дробная размерность, вероятность реализации того или иного значения функции оказываются наиболее характерными особенностями исследуемых объектов.

Целостная система, которая может быть названа одним словом , при математическом описании в первом приближении представляется действительной скалярной мерой – параметром целого. Удачный выбор параметра целого является следствием адекватности того мысленного образа изучаемого объекта, который сложился на первых этапах эмпирического исследования, реальному объекту. Параметр целого должен быть выбран таким образом, чтобы он легко определялся эмпирически или вычислялся и характер его зависимости от времени был устойчив для ряда аналогичных систем. Если мы оставляем при исследовании сложного объекта лишь одну обобщённую координату (меру, параметр целого), то в качестве неё можно использовать величину, характеризующую объём многообразия координат, более детально описывающих систему. Это может быть геометрический размер или объём, положение в пространстве, действие, энергия, масса системы, энтропия или информация, количество денег в экономике, прибыль, количество слов в языке и даже переменная возможность существования самой системы. В ряде случаев можно принять за параметр целого изучаемого объекта число элементов - квантов, которые включены в объект как в обобщённую волну [11]; если каждый из них имеет свою меру или параметр целого и эти меры аддитивны, то - суммарную меру всех объектов (квантов). Введение параметра целого подразумевает значительное информационное сжатие, и поэтому динамика его изменения не полностью определяет динамику системы. Динамика параметра целого может быть приближённо описана либо в виде итерационного процесса, либо в форме дифференциального уравнения. Качественный анализ такого рода систем с дискретным и континуальным числом состояний позволил  проанализировать возможные особенности изменения этого параметра для различных классов структур и систем.

Принципиально новые теоретические результаты были получены на пути комплексификации параметра целого и качественного исследования дифференциальных уравнений и итерационных процессов в области комплексного переменного.

Однако анализа нелинейной динамики одного, хотя и удачно выбранного, параметра целого обычно бывает недостаточно. При более детальных исследованиях вводится несколько обобщённых координат, изменение которых более подробно характеризует динамику системы. В соответствии с идеями Г. Хакена [14] и Р. Г. Баранцева [1-5] можно предположить, что оптимальным с точки зрения асимптотического анализа является тринитарное описание динамической системы. Теория нелинейных динамических систем с конечным числом координат в настоящее время интенсивно развивается. Предложены различные формы классификации систем и их математических моделей .

Всякая материальная самоорганизующаяся система обменивается с окружающей     средой (полем)

 

                                                         Энергией

                                                           /         \

                                           Материей----- Информацией.

 

Введение при анализе системы и поля времени в качестве основного параметра, определяющего динамику системы, наряду с непрерывным фазовым пространством, позволяет обратить внимание на одну очень важную особенность взаимодействия системы и её поля – на волновой характер выделяемых нами из окружающей природы структур [12].

Детальное качественное и количественное исследование взаимодействия полей и структур должно проводиться в рамках континуальных моделей, то есть для его математического описания должен использоваться аппарат линейных и нелинейных дифференциальных уравнений в частных производных и связанных с ними бесконечномерных математических групп преобразований. Однако, получение и анализ решений этих уравнений на первых этапах исследований часто оказывается нецелесообразным, а иногда, и невозможным. Более адекватным в этом случае является использование качественных методов, которые, в частности, включают классификацию волновых структур, порождаемых континуальными полями.

Нами предложена классификация волновых движений, структур и систем, опирающаяся на их общие волновые свойства, в рамках которой удалось проследить за характером влияния нелинейности на процесс самоорганизации - переход от классических линейных волновых движений к динамическим структурам и сложным самоорганизующимся транспортно-информационным системам.

Классификация в соответствии с тринитарным принципом проводится по трём параметрам:

 

                               Характер взаимодействия с другими системами

                                         /                                              \

                                      Тип ---------Степень нелинейности.

 

I. Классификация по типу:
1. Обобщённые волны, представляющие собой классы идентичных или почти идентичных объектов (квантов).

2. Вероятностные волны, характеризующие изменение плотности вероятности (или эквивалентной ей волновой функции) отыскания системы или структуры в одном из возможных для неё состояний из континуума допустимых состояний системы.

3. Классические волны в сплошной среде, характеризующие изменение во времени и пространстве плотности какого-либо параметра или связанной между собой системы параметров сплошной среды.

 

 

 

                                                       Классические волны в сплошной среде

Классификация по типу                                      /                  \

                                                    Обобщённые волны------Вероятностные  волны

 

II. Классификация по характеру взаимодействия с другими системами, аналогичная классификации конечномерных динамических систем :

1. Свободные (собственные) волны.

2. Вынужденные волны.

3. Автоволны.

 

                                                                                         Вынужденные волны

Классификация по характеру взаимодействия                    /                      \

                                                                                  Свободные волны----Автоволны

 

III. Классификация по степени нелинейности.

 

1. В качестве первого класса рассматриваются все волны относительно малой амплитуды, математическое описание которых может быть дано в виде совокупности решений линейных волновых уравнений в частных производных.

2. Ко второму классу, названному нами умеренно - нелинейными волнами, отнесены различные формы ударных волн в сплошных средах, солитоны, а также резкие изменения и скачки тех или иных параметров в однородной среде и границы раздела сред. В качестве подкласса сюда могут быть отнесены диссипативные континуальные структуры и структуры, формируемые в результате возникновения режимов с обострением [15]. Предельным случаем такого типа волн может служить введённая нами в рассмотрение суперударная комплексная волна, отыскание которой в природе составляет отдельую проблему [13 ].

3. К третьему классу, названному нами вихревыми ударными волнами, отнесены вихревые (спиновые) структуры, формируемые, как это нам удалось показать на примере решения модельных задач,  вследствие пространственной потери устойчивости  формы умеренно - нелинейных волн.

4..К четвёртому классу, названному нами грибовидными структурами, отнесены структуры мультипольной природы, формируемые из совокупности вихревых структур и вторичных умеренно нелинейных волн – вихревых пелён, возникающих в результате самопересечения фронтов волн второго класса. Различные модификации и комбинации грибовидных структур  составляют основу практически всех объектов живой и неживой природы.

5. К пятому классу отнесены структуры, названные нами древовидными (или сетевыми), бифуркационная динамика которых может быть описана методами математической теории сетей и графов, в частности при помощи теории математических деревьев .

6. К шестому классу мы отнесли сложные самоорганизующиеся системы, названные нами транспортно-информационными, являющиеся результатом трансформации и взаимодействия вихревых, грибовидных и древовидных структур и волн более низких классов.

Описанные шесть классов могут быть объединены в две системные триады

 

 

 

                                               Триада нелинейных волн

 

                                              Вихревые ударные волны

                                                 /                           \

                          Линейные волны------------Умеренно-нелинейные волны

 

                                       Триада структур и систем

                                                  

                                 Транспортно-информационные системы

                                        /                                          \

                            Грибовидные структуры-----Древовидные структуры

 

Несмотря на то, что четвёртый, пятый и шестой классы структур и систем встречаются и в неживой природе, наиболее широко они распространены в биологических и социальных объектах. Поэтому общие закономерности их динамики оказываются важными не только для физических и химических исследований, но, главным образом, для наук о Вселенной, Земле, биологии и наук о Человеке и Обществе.

Описанная  классификация нелинейных волн, структур и систем включает в себя в качестве шестого класса транспортно-информационные системы. К этому классу относятся реки и моря, атмосфера, гидросфера, живые организмы (в том числе и человек), биоценозы, а также производственно-транспортные системы социума, экономика, язык, культура, Internet, Synergonet (смотри [8]-[9]), планеты, звёзды, галактики, Вселенная.

При этом включение транспортно-информационных систем в общую классификацию волновых движений позволяет рассматривать их свойства и динамику их развития с единых позиций, применимых к любым структурам, обладающим волновыми свойствами. Они являются одной из наиболее характерных, а, возможно, единственной формой самоорганизующихся систем, обеспечивающей существование грибовидных структур. Последние, в частности, могут представлять собой совокупность вихревого тора (диполя) и «ножки», связывающей эту структуру либо с материнской границей, либо с другими грибовидными структурами. Совокупность связанных между собой грибовидных структур обычно образует многополюсную транспортно-информационную систему, представляющую собой ряд дипольных центров (шляпок грибовидных структур) и связывающие их транспортные артерии – ножки грибовидных структур.

В качестве примера приведём данное М. А. Басиным и И. И. Шиловичем [8, 9] определение одной из таких систем - Internet:

«Это большая сложная транспортно-информационная система из грибовидных (дипольных) структур, шляпка каждой из которых (собственно диполи) представляет собой мозг человека, сидящего за компьютером (или мобильным телефоном), в совокупности с самим компьютером (или мобильным телефоном), который как бы является искусственным продолжением мозга, а ножки, например, телефонная сеть, соединяющая компьютеры, или эфир, через который передаются радиоволны (от сотового телефона)» .

Разветвлённая транспортно-информационная система, во-первых, покрывает достаточно густой сетью ту часть поверхности или пространства, в которых она расположена, а во-вторых обеспечивает управляемый транспорт материи, энергии и информации к любым элементам системы. На наш взгляд, именно развитие транспортно-информационных систем и является единственным способом, который придумала природа, а за ней и человек, для преодоления всеобщего роста энтропии, а также выработки и быстрой передачи не только материи и энергии , но и информации.

Каковы же с этих позиций основные свойства транспортно-информационных систем?

А) Открытость системы. Система обычно устроена таким образом, что в узлах системы (полюсных шляпках грибов) происходит обмен материи, энергии и информации, поступающей извне и (или) вырабатываемой внутри системы.

Б) Существуют собственные транспортные элементы системы - ножки грибов- покрывающие тонкой сетью всю площадь или объём, занимаемый транспортной системой, которые осуществляют функцию доведения материи, энергии и информации до каждого элемента транспортной системы.

В) Возможно разделение функций выработки, приёма, переработки и передачи материи, энергии и информации между отдельными элементами системы, резервирование функций.

Г) Транспортные системы по мере усложнения формируют иерархическую структуру – как сама транспортная система, так и её элементы и подсистемы представляют собой грибовидные и древовидные  структуры различных масштабов.

Д) Иерархичность транспортно-информационных систем определяет квази-фрактальность их геометрии.

Создаваемые человеком транспортные и информационные системы должны строиться таким образом, чтобы учитывать указанные выше свойства естественных систем.

Необходимость выживания в условиях изменения внешней среды заставляет транспортные системы вырабатывать внутренние информационные управляющие механизмы- контроллеры. Всякой самоорганизующейся транспортно-информационной системе можно сопоставить целостную триаду :

 

 

 

 

                                                               Поле

                                                (Ближнее и Дальнее)

                                                     /                     \

                                              Структура-------------Контроллер

                              (Основная часть системы)-----------(Управляющая подсистема).

 

Структура (основная материальная часть системы) - часть системы, которая взаимодействует с полем, в основном, на материальном и энергетическом уровне.

Поле (ближнее и дальнее) – это внешняя по отношению к системе совокупность объектов, интенсивно взаимодействующих с системой. Поле может быть условно разделено на ближнее и дальнее. Для исследования взаимодействия дальнего поля с системой могут быть использованы асимптотические методы [1].

Контроллер (управляющий механизм) – внутренний механизм системы, обеспечивающий выбор из числа возможных исходов бифуркационного события или процесса, того, который приведёт к наиболее устойчивому состоянию системы.

Появление контроллера включает в действие механизм эволюции. Развиваются в непосредственной связи между собой все три элемента триады. Возникает тройное резонансное взаимодействие (по-видимому, здесь действует механизм структурно-волнового резонанса) [12], приводящее к увеличению сложности и динамической устойчивости (увеличению числа возможных исходов бифуркационных событий  и увеличению количества информации, хранимой и перерабатываемой контроллером). Анализ триады сложной волновой транспортно-информационной системы показывает, что все её элементы могут быть исследованы более глубоко и для каждого из них может быть построена своя внутренняя системная триада.

Структура характеризуется тремя главными координатами:

мерой, типом и иерархией

                                                       Тип

Структура                                   /         \ .

                                             Мера----------Иерархия

 

Мера – характеризует величину основного параметра структуры, который часто (но далеко не всегда) совпадает с параметром целого всей системы.

Тип- Структура может быть отнесена к одному из классов волн, вихревых, грибовидных или древовидных структур или транспортно-информационных систем, в соответствии с изложенной выше классификацией.

Иерархия – Сложные системы обычно состоят из подсистем различных масштабов, связанных между собой. Каждая из них может иметь свою меру и свой тип. Вместе они образуют иерархию сложной системы.

Аналогичная триада формируется в управляющем механизме.

 

                                                                Информация

Контроллер                                          /                   \

                                                           Управление-------Память

 

Управление. Главная «цель» управляющего механизма – управление исходами бифуркационных событий (событий, которые могут иметь конечное или бесконечное множество исходов). Управление производится путём изменения иерархической структуры объекта, установления новых внутренних связей, а также активации, разрушения или резервирования старых.

Информация – Для управления необходимо получение информации об изменениях, происходящих в самой системе и во внешнем поле.

Память - Специальный механизм сохранения и переработки полученной ранее информации, а также своевременного использования её для целей управления.

Контроллер - это механизм управления бифуркационными процессами, в которых участвует система.

Контроллеры могут быть как минимум двух типов

1.   Контроллер, порождающий структуру и определяющий её внутреннее развитие.

2.   Контроллер, обеспечивающий устойчивое существование структуры, выбор её поведения при взаимодействии с полем, способный до начала событий изменять вероятности реализации возможных результатов, а также осуществляющий в момент свершения события выбор того или иного конкретного результата – гомеостатический контроллер.

1.   Контроллер, порождающий структуру.

Он может находиться как вне структуры, в её поле, так и внутри самой структуры.

Порождающий контроллер должен обеспечивать существование и воспроизводство обобщённой волны, в которую структура входит как квант.

Здесь возникает новая масштабная и одновременно целостная триада

 

                                                             Поле

                                                          /           \

                                               Квант--------Обобщённая волна

 

2.   Гомеостатический контроллер.

В результате формирования системы и выхода её на режим стабильного существования возникает стационарный режим обмена веществом, энергией и информацией между структурой и полем, при котором параметр целого системы остаётся близким к постоянной величине. Устойчивость этого режима и безопасность системы обеспечивает гомеостатический контроллер. Основной принцип его действия – обобщённый принцип отпицательной обратной связи. Он реализуется через управление вероятностями исходов бифуркационных событий и процессов. Любое возмущение внешнего поля приводит к возмущению параметров системы. При этом включается нелинейный механизм стабилизации, возвращающий гомеостаз.

Транспортно-информационные системы, в свою очередь, могут быть классифицированы по степени нелинейности (сложности).

1. Системы квази - детерминированного типа, бифуркационные процессы внутри которых оказывают лишь интегральное влияние на их макропараметры. Основным свойством таких систем является значительная разница между масштабами самой системы как обобщённой волны и отдельными элементами (квантами), её формирующими, а также близость параметров квантов. Границы таких систем, являющиеся обычно волновыми структурами, относящимися ко второму и третьему классу предложенной нами классификации, во многом определяют их динамические свойства. Для изучения систем квазидетерминированного типа существуют глубоко разработанные методы равновесной и неравновесной статистической физики и термодинамики а также механики сплошных сред. Большинство макроскопических объектов неживой природы относится к этому подклассу.

2. Транспортно - информационные системы, у которых реализуется иерархическая материальная и информационная связь между уровнем системы-волны и элемента-кванта. В таких системах обычно выстраивается масштабная иерархия подсистем, каждая из которых может обладать волновыми свойствами структур классов более низкой степени нелинейности. Эта масштабная иерархия имеет квазифрактальный характер.

3.Транспортно-информационные системы, способные к размножению, то есть к формированию себе подобных систем. Способность к размножению не является прерогативой только транспортно-информационных систем. Практически это свойство в той или иной степени характерно для любых колебательных и волновых систем, начиная с линейных колебаний и волн. Однако, когда мы переходим к рассмотрению транспортно-информационных систем третьего подкласса, то их размножение может иметь специфический характер, проявляя, особенно у живых систем, такую сложность, которую невозможно даже помыслить у волн и структур более примитивных классов.

4.Транспортно-информационные системы, способные моделировать свою динамику и динамику окружающей среды - поля и выбирать близкие к оптимальным  модели бифуркационного поведения. Именно у таких систем интенсивно развивается, определяя их эволюцию, внутренний контроллер.

5. Транспортно-информационные системы, обладающие сознанием и творческими способностями.

Так как возникновение и эволюция контроллера является принципиально важным фактором, отличающим сложные транспортно-информационные системы, то причины его появления и механизм действия требуют специального рассмотрения. Если бы все события  в природе были детерминированы, а процессы, происходящие со всеми структурами, были заранее предопределены, то никакой потребности в контроллере бы не возникло. Информация и представление о ней возникают только как следствие существования неопределённости при совершении бифуркационных событий.

Однако это только одна сторона информационного процесса. Возможность существования в природе бифуркационных событий и процессов порождает принципиальную неполную предсказуемость будущего, а следовательно, возможность управления будущим путём выбора одного из возможных исходов. Возникает  необходимость вероятностного предсказания будущего – знания о будущем. Переход от информации о прошлом к информации о будущем, знанию, - это творческий процесс. Резкий скачок информации о будущем может произойти без дополнительного получения информации о прошлом и наоборот, можно получать бесконечное количество информации о прошлом, не извлекая из неё знания. (это может быть проиллюстрировано на примере суперударной волны [13].

При изучении системы, управляемой контроллером, необходимо не только анализировать динамику её основной материальной структуры и строить соответствующие математические модели, но также знать принципы действия контроллера и уметь моделировать процесс создания им моделей поведения. Здесь возникает новая триада

                                                    Исследователь

                                                       /                \

                                     Структура--------------Контроллер

 

Вся окружающая нас действительность представляет собой синергетическое взаимодействие волн, структур и систем различной природы. В качестве примера могут быть рассмотрены последние катастрофические события. Взаимодействие небесных тел: Земли и Луны, - наложившееся на внутренние процессы, происходящие в Земной коре, привело к землетрясению - возникновению разрывов в земной коре – формированию вихревых ударных волн третьего класса. Воздействие этого процесса на поверхность океана породило мощную уединённую волну (солитон)- цунами. Резонансное воздействие этих волновых структур на побережье Японии привело к значительным разрушениям в транспортно-информационной системе, созданной японским этносом, одной из подсистем человеческого общества. Одновременно погибли тысячи людей, транспортно-информационных систем значительно меньших масштабов, но обладающих наивысшей из известных нам степенью нелинейности. Однако эти события имеют продолжение и оказывают своё влияние на всю биосферу Земли и всё человеческое общество. Частичное разрушение информационно-транспортной структуры Японских островов привело к возмущениям в экономике Японии и отразилось на котировках ценных бумаг на биржах всего мира. Частичное разрушение атомной электростанции в Японии привело к нарушению управления ядерной реакцией и опасности неуправляемых процессов ядерного взрыва – формирования грибовидных структур больших масштабов,- что, в свою очередь может привести к необратимым изменениям в биосфере и человеческом обществе. Если подобные волновые возмущения смогут быть погашены контроллером человечества, то все разрушения инфраструктуры будут нивелированы, если нет, то цепочка катастрофических событий, в которых возникают и взаимодействуют волны, структуры и системы различных классов, будет продолжена (к счастью, возмущения на этот раз были погашены).

Изучение транспортно-информационных систем потребовало введения таких понятий как бифуркационное событие, то есть событие, имеющее дискретное или континуальное множество потенциально возможных исходов; бифуркационный процесс, представляющий последовательность бифуркационных событий. Введение этих понятий привело к модификации существующих представлений об энтропии и информации сложных систем. Наряду со стандартным определением количества информации как меры уменьшения неопределённости нами рассмотрено представление об информации как результате отождествления состояний, структур и событий. Наряду с представлением об информации о прошлых событиях введено представление об информации о будущем – знании, которое базируется на отождествлении нескольких аналогичных событий. Введено двухпараметрическое рассмотрение энтропии и информации сложной системы,      использование которого позволило установить многосторонние связи между информационными характеристиками системы и границами раздела сред  как нелинейными волнами второго класса.

Приближённое графическое представление последовательности связанных между собой бифуркационных событий мы назвали графом структур и событий. У исследуемой системы можно выделить периоды, характеризуемые двумя характерными типами поведения.

а) Периоды сравнительно плавных изменений, когда система приближённо может быть описана как детерминированная и для её описания пригодны методы теории динамических систем (русла в терминологии Г. Г. Малинецкого). Этим периодам соответствуют рёбра графа структур и событий  [16].

б) Периоды резких бифуркационных изменений, в результате которых система может с некоторой вероятностью приобрести одно из множества возможных состояний  – бифуркационные события (джокеры в терминологии Г.Г. Малинецкого [16]).

Качественный и количественный анализ графа структур и событий показал, что кроме структурной проекции, характеризуемой триадой параметров (мерой, типом классификации, иерархией), необходимо рассматривать бифуркационную проекцию графа, включающую в себя различные возможные варианты будущего поведения системы.

Подчиняясь собственным законам, внутренняя динамика системы порождает внутреннее время, которое согласуется с внешним темпом событий в окружающей среде. В качестве одного из примеров описания этого процесса нами предложена математическая модель внутреннего (линейного) времени и внешнего (экспоненциального времени) . Если в терминах внутреннего времени динамика изучаемого объекта удовлетворяет системе линейных дифференциальных уравнений, справедливой на бесконечном промежутке времени, то в терминах внешнего экспоненциального времени система имеет начало и конец, что соответствует конечному внешнему времени существования реальных систем. Введение экспоненциального внешнего времени и комплексификация дифференциальных уравнений позволили построить на уровне параметра целого новые математические модели возникновения и разрушения сложных систем.

Предложенный подход позволил также решать и обратные задачи - по экспериментальным данным о поведении системы в катастрофических обстоятельствах определить коэффициенты соответствующей системы уравнений. Полученные результаты позволяют не только моделировать поведение сложных систем при катастрофических событиях и определить предвестники катастроф, но и разработать мероприятия по их предотвращению. Предложенные модели проверены на ряде уже свершившихся катастрофических событий, в частности, при исследовании биржевых торгов в момент кризиса. По нашему мнению, наиболее эффективными они будут при математическом моделировании происходящего в настоящее время мирового экономического и структурного кризиса, отдельные проявления которого были предсказаны М. А. Басиным и И. И. Шиловичем при исследовании динамики развития Internet и превращения её в Synergonet [8, 9].

Остановимся на применении синергетической тринитарной методологи при анализе проблем жизни и динамики человеческого общества. Одними из главных свойств живых объектов являются их рост и размножение, тесно связанные между собой. В качестве параметра целого при математическом описании элементов триады: клетка-человек-человечество – нами была принята масса. Это позволило с единых позиций рассмотреть динамические процессы на различных уровнях масштабной иерархии и предложить для совместного анализа роста и размножения клеток и роста организма единую математическую модель, представляющую собой комбинацию итерационного процесса для степенных функций комплексного переменного и нелинейного дифференциального уравнения. Эта модель позволяет, в отличие от существующих стандартных моделей, одновременно учесть рост и размножение клеток организма. Предложенная модель может быть легко модифицирована и обобщена на различные типы ветвящихся процессов, каждый участник которых обладает двумя свойствами – роста и деления. Модель содержит три управляющих параметра, которые могут изменяться на каждом шаге размножения, что позволяет учесть влияние внешних условий на динамику размножения и роста. (Авторы благодарят Р.Г. Баранцева за ценные рекомендации по усовершенствованию предложенной модели).

Для описания динамики параметра целого человеческой популяции, имеющей иной закон зависимости изменения массы от времени, нами была предложена математическая модель, включающая комплексные переменные, анализ которой позволяет не только предсказать гиперболический рост человеческой популяции, наблюдавшийся на этапе демографического взрыва, но и демографический переход, соответствующий  наступающей в настоящее время стабилизации количества людей. Комплексификация модели позволила наряду с результатами, полученными ранее С. П. Капицей [17] для действительного параметра целого, проанализировать новое уравнение, которое, в соответствии с нашим предположением описывает динамику изменения информационного параметра человеческой популяции. В соответствии с исследовавшейся моделью в настоящее время человечество переживает процесс, называемый демографическим переходом, когда интенсивный рост числа людей сменяется стабилизацией, сопровождающейся кризисами, в том числе и экономическими. Можно предположить, что наблюдающийся сейчас экономический кризис является проявлением происходящего в настоящее время качественного изменения динамики роста человеческой популяции. Однако, исследованная модель соответствует лишь одному из возможных будущих сценариев динамики человеческой популяции. В настоящее время могут быть рассмотрены ещё два возможных сценария динамики: резонансная (пессимистическая) модель, поддерживаемая экологами, соответствующая катастрофическому или плавному сокращению числа людей, истощивших ресурсы Земли и не нашедших альтернативных источников существования; космическая (сверх - оптимистическая) модель соответствующая выходу человечества за пределы Земли, а затем и Солнечной системы.

Проекция введённой выше триады

                                                   Поле

                                                 /           \

                                     Структура - Контроллер

на человеческое общество может выглядеть следующим образом:

                                                Космос

                                              /               \

                  Человеческая популяция – Государство.

 

Космос – поле человечества, включает ближнее поле – планету Земля. В качестве дальнего поля можно рассматривать Солнечную систему и даже всю Галактику.

Человеческая популяция – совокупность людей совместно с их  собственностью, понимаемая как некий материальный объект.

Государство – под этим термином мы понимаем контроллер человеческой популяции - систему, управляющую взаимоотношениями между людьми и связями человечества с внешней средой - Космосом.

Эта системная триада может быть дополнена связанной с ней триадой взаимодействия, действующей на стыках элементов основной триады:[1]

 

 

 

 

                                                   Тело   -   Дух

                                                         \         /

                                                          Душа

 

Тело - это процессы материального взаимодействия Человечества с окружающей природой, в результате которых обеспечиваются все элементы материального существования человечества как биологического вида. Сюда относятся, в основном, процессы обмена материей и энергией.

Душа – результат взаимодействия контроллера человечества, условно названного нами         государством, с естественно выстраивающейся социальной иерархической системой, формируемой   отдельными людьми и их группами.

Дух - процессы взаимодействия контроллеров человечества и Космоса – окружающей среды – своего рода совместный творческий потенциал человечества и Космоса.

Введённые триады могут быть объединены в единую схему [10].

Аналогичная система двух связанных триад может быть построена и для отдельного человека:

 

                                                    Внешняя среда человека

                                                   /                                            \

                                   Организм человека - Управляющая система

 

Внешняя среда человека – объекты, определяющие жизнедеятельность отдельного человека, в том числе и люди, составляющие часть человечества или всё человечество в последнее время такой средой всё больше становится Synergonet.

Управляющая система – контроллер, осуществляющий управление взаимодействием организма    человека с внешней средой и внутренней жизнедеятельностью человека.

Организм человека – материальная часть человека как системы.

К этой триаде примыкает двойственная ей триада взаимодействия:

 

                                              Обмен веществ - Интеллект

                                                  \                               /

                                               Управление организмом.

 

Обмен веществ – материальный обмен человека и внешней среды веществом и энергией.

Интеллект – информационный обмен человека с внешней средой (в том числе и общение между людьми), управляемый, в основном, нервной системой.     Управление организмом – управление процессами, обеспечивающими целостность организма, осуществляемое, главным образом, эндокринной системой.

Две последние триады также  могут быть объединены в единый комплекс.

Аналогичные связанные триады могут быть построены и для отдельной клетки:

                                                Внеклеточная среда

                                              /                                \

                                            Структура клетки – Геном

 

Внеклеточная среда – внутренняя среда организма, состоящая из других клеток и межклеточной среды.  Для клеток кожи – это также внешняя среда человеческого организма.

Геном – контроллер клетки, содержащий информацию о структуре клетки и во многом о структуре организма в целом.

Структура клетки – материальная часть клетки, в которой осуществляется обмен веществом и энергией.

Так же, как и ранее, может быть выстроена дополнительная триада взаимодействия, включающая:

 

                                         Питание---------- Информационный обмен

                                                          \                   /

                                              Управление внутренним обменом

 

Питание - энергетический материальный обмен клетки с другими клетками и системами, обеспечивающими жизнедеятельность организма.

Управление внутренним обменом – процессы управления внутренней жизнедеятельностью клетки.

Информационный обмен - обмен информацией между контроллерами клетки и организма.

Две последние триады также могут быть объединены в целостный комплекс.     Между построенными комплексами существуют связи, наличие которых позволяет говорить о спирали резонансных взаимодействий элементов различных масштабных уровней.

Организм человека является основной частью поля отдельной клетки, тогда как человеческая популяция является основной частью поля отдельного человека. Особую роль играют связи контроллера клетки – генома со структурой человеческого организма, а, возможно, и с динамикой развития человеческого общества. Однако, не менее важны резонансные связи между контроллерами клетки, организма и человечества в целом – то есть связи между геномом, нервной и эндокринной системами и информационными структурами, создаваемыми человечеством. Геном клетки резонансно и достаточно жёстко определяет её структуру и структуру человеческого организма, в том числе и структуру эндокринной и нервной системы. Однако нервная система человека неоднозначно определяет структуру человеческого общества. Обратное же влияние внешнего поля на геном человека считается пренебрежимо малым. С таким утверждением трудно согласиться. Если изменения, происходящие с контроллером отдельного человека, практически не влияют на геном половых клеток, то длительные изменения внешней среды, поля, в котором существует человечество как вид за счёт масштабного резонанса должны вызывать приспособительные изменения генома не только за счёт отбора случайно приобретённых признаков. Эта  проблема требует своего решения именно в настоящее время, так как развитие человечества привело к резкому изменению состояния ближнего поля – биосферы и поверхности Земли, что в свою очередь за счёт обратных связей может привести к изменению генома человека.

Резонансные процессы, являющиеся комбинациями масштабных и структурных резонансов, широко распространены в биологических и социальных системах. Авторами была высказана гипотеза о том, что масштабный и структурный резонансы играли существенную роль в возникновении жизни. Наиболее ярким примером применимости концепции вихре – волнового и (или) структурного резонанса может стать проблема возникновения живого. Изложим некоторые гипотезы.

Важную роль здесь играют резонансные нелинейные процессы формирования и деформации границ, приводящие к росту информации. Двумерные границы рассматриваются в нашей классификации как одна из форм нелинейных ударных волн. В формировании и динамике резонансных грибовидных структур границы несут главную информационную нагрузку, которая для живых организмов является основной и постоянно развивающейся. Еще большую информацию несёт линия, представляющая собой пересечение двух границ. Но максимальная информационная нагрузка возникает в точке, в которой пересекаются три границы.

Существуют ли такие области в Природе? Да. Если мы рассмотрим четыре стихии Аристотеля: земля, вода, воздух и огонь,- то пересечение границ между ними должно привести к появлению малой особой области, в которой формируются структуры, элементы которой обладают максимальной неоднородностью. Побережье Мирового Океана и побережья локальных водных пространств могут рассматриваться как линии пересечения двух границ. Если в этой области локально добавить «огонь» в виде Солнечного света или вулканических извержений (проблема «чёрных курильщиков»), то реально создаются условия для возникновения и длительного существования разнообразных резонансных форм устойчивых в своей неустойчивости вихревых и грибовидных структур, которые можно отождествить с одной из форм живых организмов.

Эта гипотеза требует детальной проработки и может явиться основанием для формирования нового направления в изучении важнейшей научной проблемы возникновения жизни. Если она подтвердится, то подобный механизм может быть использован для создания принципиально новых нана – технологий, имеющих дело с объектами, лежащими на границе живого и неживого.

Однако это не единственное направление подобных исследований. Анализ динамики популяции клеток и организмов в условиях ограниченного ресурса также позволяет обнаружить резонансный путь развития. Этот путь избрала природа при создании многоклеточных животных и растений. По этому же резонансному пути, возможно, пойдёт и человеческое общество, столкнувшись с экономическими кризисами, нехваткой материальных ресурсов и ограничениями численности популяции. Формирование мегаполисов, появление и интенсивное развитие Internet с возможным переходом в Synergonet, передача всё большего числа функций международным организациям – являются свидетельствами резонансной самоорганизации, а также интенсивного развития и качественной трансформации единого общего   для всего человечества контроллера. Об этом же говорит глобальность и синхронность проявлений структурного кризиса, с которым столкнулось человечество в настоящее время. Так, например, революции в совершенно различных арабских странах произошли практически одновременно.

Пусть пространство, в котором популяция клеток или организмов может использовать природные ресурсы, ограничено и отделено от другого аналогичного пространства значительной зоной, в которой получить ресурсы для существования невозможно. Характерным примером является слизневик Dictyostelium disclodeum, который может существовать как в форме отдельных клеток (нерезонансный режим), так и в форме единого организма (резонансный режим) [14]. В фазе роста, когда ресурса достаточно, каждая отдельная клетка слизневика существует как отдельная особь. Их распространение по поверхности осуществляется по закону движения свободной биологической волны: они размножаются по экспоненциальному закону, занимая всё большую площадь. Однако, когда ресурса начинает не хватать, система переходит в состояние резонансной самоорганизации. Одна из клеток становится пейсмекером, центром структурно - волнового резонанса. Испуская специфические вещества, она создаёт новое биологическое поле, резонансно притягивает к себе остальные клетки. Формируется многоклеточная грибовидная структура, клетки которой расположены впритык друг к другу, что позволяет им поддерживать обмен веществ при значительно меньших затратах энергии, чем при независимом существовании.

Тем самым внешней средой для внутренних клеток становятся резонансно с ними взаимодействующие клетки, имеющие те же размеры и синхронизированный с ними темп обмена веществ. Резко уменьшается поверхность соприкосновения популяции с внешней средой. Каждую внутреннюю клетку кормят её соседи или  вновь образовавшиеся транспортные системы. Существование каждой клетки резонансно обеспечивается существованием всех остальных. Благодаря структурно-волновому резонансу биологические поля, создаваемые отдельными клетками усиливаются и синхронизируются, формируя биологический мультиполь. Тем самым открывается возможность для дальнейшего роста   и развития возникшего организма. Однако, законы этого роста становятся другими. Сближение внутренних клеток уменьшает скорость их роста и резко увеличивает период между размножениями. Однако этот период не становится бесконечным. Происходит резонансная синхронизация периодов существования отдельной клетки и их совокупности, определяющая большой, но обязательно конечный период существования сформировавшегося единого организма (не здесь ли таится загадка жизни и смерти многоклеточных организмов?). Резонансное взаимодействие клеток с различными районами создаваемого ими биологического поля и возможность их участия в бифуркационных событиях приводит к их дифференциации. Особенно существенными оказываются различия между граничными клетками и внутренними. Граничные клетки обладают значительно большим числом степеней свободы и по своим характеристикам приближаются к недифференцированным клеткам свободно растущей популяции. Об этом свидетельствует недавно открытая возможность клонирования многоклеточных организмов не только с использованием стволовых (недифференцированных или слабо дифференцированных) клеток зародыша, но и клеток кожи животных. Внутреннее поле организма существенно неоднородно, и его интенсивность и структура определяется внутренней геометрией организма. Поэтому его структура резонансно определяет вид дифференциации клеток, что приводит к их синхронизации с динамикой всего организма и необратимости произошедших изменений.      Совершенно в других условиях находятся клетки поверхности. Воздействие на них собственного поля организма значительно слабее, частота их размножения выше. Они более подвижны и активны.

Так как резонансные изменения внешнего поля, вызываемые синхронизированной группой клеток, значительно превышают интенсивность поля, индуцированного аналогичной группой свободно живущих клеток, то зона влияния сформировавшегося организма оказывается значительно выше. Граничные клетки могут формировать длинные нити, связанные с основной резонансной грибовидной структурой, и расположенные по силовым линиям нового биологического поля (ножки грибовидных структур), и в новых местах рождать новые грибовидные структуры, связанные с первичными. Разграничение свойств и функций клеток позволяет популяции строить два типа связанных между собой поселений: концентрированные «шляпки» грибовидных структур с плотным расположением клеток, создающих мощное резонансное биологическое поле, и нитевидные «ножки» грибовидных структур, охватывающие большие поверхности, площадь которых пропорциональна мощности этого поля. Нитевидные структуры служат для активного добывания пищи и получения информации, а также для их транспортировки. Тем самым многоклеточные организмы благодаря сложным резонансным процессам вводят в свою структуру существенную дифференциацию, что приводит в конце концов к формированию не только нового организма, но и его собственного контроллера. Часть функций управляющего механизма отдельной клетки передаётся постепенно формирующемуся контроллеру многоклеточного организма. Почти хаотическое движение клеток в свободной биологической волне, имеющее большое число практически равноправных степеней свободы движения и роста каждой отдельной клетки переходит в относительно упорядоченное движение системы, в котором рост и движение каждой клетки резонансно синхронизировано с движением остальных клеток. В системе с необходимостью возникает внешний по отношению к отдельным клеткам гомеостатический контроллер, действующий путём трансформации биологического поля, например, путём синхронного электромагнитного взаимодействия отдельных клеток, или выработки химических веществ, синхронизирующих поведение отдельных клеток (зачаток эндокринной системы).

Резонансное формирование многоклеточных структур явилось важнейшим шагом в развитии биосферы. С их формированием появились новые, макроскопические кванты живой материи, существование которых позволило регулировать скорость размножения и одновременно увеличить сферу существования живых организмов. Но главное, - возник принципиально новый, внеклеточный механизм управления совокупностями клеточных структур (гомеостатический контроллер организма). За счёт ограничения числа степеней свободы одной клетки организм приобрел большую вероятность для практически невозможных ранее степеней свободы на более высоком масштабном уровне.

Некоторые основные закономерности резонансной самоорганизации клеточных популяций оказываются характерными и для социальных систем. В частности, события, происходящие в настоящее время внутри человеческого общества, связанные с демографическим переходом, во многом аналогичны описанным выше. Особенно явно это стало заметно после 80-х годов двадцатого века, когда окончился демографический взрыв и стали более интенсивно развиваться процессы самоорганизации человечества как единой системы (демографический переход). Резкое увеличение размеров и этажности городов, где люди живут почти вплотную друг к другу, во многом аналогично формированию грибовидной структуры слизневика. Всё в большей степени внешней средой для отдельного человека становятся другие люди, тесно с ним взаимодействующие, что приводит к необходимости создавать и совершенствовать транспортные системы для снабжения каждого человека необходимыми ему ресурсами. Всё более развивается единый обменный эквивалент – деньги, определяющий возникшие экономические взаимоотношения между людьми. В последние годы в связи с демографическим переходом значительные качественные изменения происходят и в экономике,  к изучению которой также может быть применена концепция вихре - волнового и структурного резонанса. Происходящий в настоящее время экономический и структурный кризис является одной из форм происходящей резонансной перестройки.

Для того, чтобы выжить в мире, который не только даёт пищу, воду и воздух, но и приносит природные катастрофы, внутренние раздоры, болезни, врагов и конкурентов, необходимо уметь предсказывать грядущие опасности. Для решения этой проблемы природа наделила каждого человека самым мощным среди животных гомеостатическим контроллером – нервной системой. В процессе развития человечества всё большую роль начинали играть не только непосредственное получение информации, но передача полученной информации другим людям, а также её переработка. Развитие звуковой речи характеризовало очень глубокий уровень переработки         информации. Для того, чтобы назвать какой-либо объект, необходимо было не только выделить его из окружающего мира, но и включить в качестве кванта в некоторую обобщённую волну, всем квантам которой было присвоено одно и то же имя, один и тот же символ. Одновременно с возникновением речи был сделан первый шаг к созданию отличной от генетической общечеловеческой памяти – создание каменных скульптур и наскальных изображений, явившихся прообразом изобразительного искусства, сохраняющего образную информацию вне человеческого мозга. Следующим шагом в отчуждении информации от отдельного человека  и передаче её общему контроллеру человечества было изобретение письменности - этой задержанной на долгое время речи. Появились новые символы -  символы символов – цифры, буквы и иероглифы. Так возникла       первая символьная память, носителем которой стал не отдельный человек, а некий материальный объект, пользоваться которым мог любой человек, умеющий читать. Появилась и стала интенсивно развиваться индустрия вне-мозгового сохранения словесной информации. Письменность – это гигантский скачок в формировании контроллера человечества как единой волны, так как с её появлением впервые появилась потенциальная возможность создать носители существенно          переработанной информации, необходимой для всего человечества, позволяющие длительно хранить эту информацию вне человеческого мозга. Развитие письменности и создание хранилищ рукописей явилось важнейшей формой сохранения общечеловеческой информации – мудрости человечества. Именно в Священных книгах хранились основные положения всех древних религий и учений. Возникла возможность появления почты, передачи письменной информации на произвольные расстояния. Одновременно со средствами запоминания и передачи информации развивались и средства сжатия общечеловеческой информации и превращения её в знание, которое началось с появления языка. Проявлениями этого процесса явились создание и запоминание религиозных учений, в которых сохранялась память о приобретённых ранее знаниях и на их основе давались рекомендации на будущее, определялась мораль человеческого общества – правила взаимоотношения людей, обеспечивающие их совместное выживание. Существенную роль в этом процессе сыграло появление научного знания – то есть отыскание общих качественных и количественных закономерностей окружающего мира и человеческого общества. Следующим важнейшим шагом в развитии информационных структур явилось изобретение книгопечатания – появилась не существовавшая до этого момента возможность создания неограниченного числа копий наиболее важных для отдельных людей литературных и научных произведений. XIX и XX века. принесли человечеству поток новых средств передачи и хранения информации: фотография, телефон, телеграф, радио, телевидение, аудио- видео- аппаратура, компьютеры, мобильные телефоны. При этом всё большую и большую роль стали играть запоминание звуковых и визуальных образов, что значительно изменило форму информационных потоков, циркулирующих в человеческом обществе. Затем появился Internet. Функционирование Internet первое время   практически не сказывалось на потоке информации, циркулирующей в человеческом обществе, и влияющей на его поведение. Однако сегодня Internet - это уникальная глобальная информационная система, управляющая большей частью информации, циркулирующей в человеческом обществе. Развитие Internet является в настоящее время индикатором изменений контроллера человечества. Анализ  динамики её развития позволяет изучить процессы резонансной самоорганизации контроллера человечества и превращения его в принципиально новую структуру, названную М.А. Басиным и И. И. Шиловичем – Synergonet [8],[9].

Проследим вслед за ними некоторые этапы на пути в Synergonet:

1 Стандартный компьютер с момента своего появления являлся одним из средств преобразования информации. Компьютерные программы содержат некоторые необходимые для предсказания будущего полученные ранее  исходные данные и детерминированный алгоритм преобразования их в другие данные, необходимые для построения элементов будущих процессов, входящих в граф структур и событий. Первоначально компьютеры были использованы лишь для значительного ускорения рутинной вычислительной работы по преобразованию полученных человеком данных из одной формы в другую, более удобную для практических задач.

2. Компьютерная память – второй этап в процессе передачи информационных потоков компьютерным системам. Компьютер принимает на себя функции библиотеки концентрированной информации.

3. Появление первых сетей – сначала в архитектуре компьютера для реализации принципа многозадачности разделением времени решения. Затем появление сетей, обеспечивающих информационное взаимодействие многих людей, коллективов, их компьютеров и корпоративных сетей при решении всё более сложных задач. Фактически этот третий этап продолжается и в настоящее время в процессе развития Internet. Однако данный процесс имел два основных под-периода, отличающихся объёмом включения в процессы развития сетей случайного элемента и порождение новых связей между людьми. Первые связи между компьютерами были практически детерминированы и определялись связями между людьми, которые существовали и до введения компьютеров.

4. Существенное принципиальное значение того, что произошло с развитием Internet, это то, что в компьютерный мир был внедрён рынок – с атрибутами самоорганизации. При этом впервые возникло глубокое обратное влияние Internet на связи между людьми, в частности, на их экономические отношения. Cейчас уже говорят о том, что торговля через Internet скоро полностью заменит другие формы торговли.

5.А это, в свою очередь, меняет структуру человеческого общества и является первым шагом к формированию принципиально новой структуры, – Synergonet.  Synergonet - результат совместной резонансной самоорганизации человечества и Internet., приводящей к качественному изменению контроллера человеческого общества, а следовательно и самого общества. Интенсивное развитие сети мобильных телефонов и происходящее в настоящее время их резонансное объединение  с Internet – одно из свидетельств этого процесса.

6. Synergonet берёт на себя во всё большей мере роль глобального контроллера , забирая всё больше функций у человеческого мозга  и  Государства. Все информационные ресурсы переносятся в Synergonet. Возникает проблема управления со стороны Internet без участия человека производственными процессами и решением политических и социальных проблем.

7. При этом возникает опасная для человечества перспектива возникновения Synergonet 2.[9].  Сеть может приобрести свой собственный внутренний контроллер, целью которого может стать выживание Сети, не обязательно дружественный контроллеру человеческого общества. Изучение этой проблемы в настоящее время представляется нам особенно важным. Ведь нынешний глобальный структурный кризис совпал по времени с третьим бифуркационным кризисом Internet, связанным с переходом системы Internet–Человечество в фазу Synergonet, предсказанным М.А. Басиным и И.И. Шиловичем ещё в 1999 году.

 

   Литература.

 

1. Андрианов И. В., Баранцев Р. Г., Маневич Л. И. Асимптотическая математика и синергетика: путь к целостной простоте. М.: Едиториал УРСС.2004. 304с.

2. Баранцев Р. Г. Нелинейность – когерентность – открытость как системная триада синергетики//Мост 1999. № 29. С.54-55.

3. Баранцев Р. Г. Синергетика в современном естествознании. М.: Едиториал УРСС. 2003.144с.

4. Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

5. Баранцев Р. Г. История семиодинамики: документы, беседы, комментарии. М.-Ижевск НИЦ «Регулярная и хаотическая механика». 2006. 376 с.

6. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168 с.

7. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144 с.

8. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71 с.

9. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.

10. Басина Г. И., Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с.

11. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.

12. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с

13. Басина Г. И., Басин М. А. Синергетика. От чисел Басина до Synergonet. Этюды

Посвящено столетию со дня рождения выдающегося учёного Басина Абрама Моисеевича

14. Хакен Г. Синергетика. М.: Мир. 1980. 414 с.

15. Режимы  с обострением. Эволюция идеи: Законы коэволюции сложных систем. М.: Наука. 1998. 255 с

16. Управление риском: Риск. Устойчивое развитие. Синергетика. М.: Наука.2000. 431 с.

17. Капица С. П. Общая теория роста человечества. Сколько людей жило, живёт и будет жить на Земле. М.: 1999.

 

 

 

 

 

 

 

 

 

 

 

                                                      Этюд 17

                              Линейные волны и волновые  резонансы.

 

1.                                                                                                                                                                                                             Анализ одномерного линейного волнового уравнения .

 

    Специфические резонансные явления наблюдаются также при взаимодействии волновых движений, так как любая синусоидальная волна может рассматриваться как бесконечная цепочка гармонических осцилляторов, каждый из которых может вступать в резонансное взаимодействие с другими осцилляторами и с внешними возмущениями. Особое, интенсивно развивающееся направление исследований представляет анализ взаимодействия цепочек, состоящих из большого числа связанных между собой осцилляторов, подверженных внешнему воздействию. Здесь проявляются специфические особенности, которые затем более чётко становятся видны при анализе волновых движений, а кроме того, возникают резонансные явления, которые отсутствуют как у систем с малым числом степеней свободы, так и у волновых систем [10]. Эти особенности могут оказаться важными для транспортно-информационных систем, имеющих масштабную иерархию осцилляторов или обобщённых волн. Их использование позволит решить вопрос о масштабных временных и пространственных резонансах в таких системах и о распределении информации, массы и энергии на различных уровнях иерархии.

    На примере линейного волнового уравнения с одной пространственной переменной, которое является математической моделью большого числа природных и социальных явлений, покажем возможность существования тех типов волновых резонансов, которые являются аналогами временных резонансов в конечномерных системах.

В случае, если динамика системы описывается большим числом переменных, благодаря введению дополнительных гипотез, например, гипотезы эргодичности, удается упростить рассмотрение поведения динамических систем путем введения небольшого количества новых осредненных переменных типа плотности, осредненной скорости, тензора напряжений, температуры, энтропии и новых уравнений связи между этими величинами, базирующихся на основных законах механики, термодинамики и дополнительных предположениях о связях между кинематикой движения и тензором напряжений. Задача исследования динамической системы сводится к исследованию гипотетической сплошной среды с бесконечным числом скрытых переменных и с конечным числом функций от пространственных и временной координат, удовлетворяющих системе уравнений в частных производных. Одним из фундаментальных решений системы линейных дифференциальных уравнений в частных производных в случае одной пространственной переменной является решение в виде линейной синусоидальной волны, описываемой в одномерном случае уравнением:

 

.                            (2.1)

 

Здесь u-скаляр, характеризующий состояние среды, удовлетворяющий линейному дифференциальному уравнению в частных производных

 

,                                   (2.2)

 

где  - линейный дифференциальный оператор с постоянными коэффициентами. Анализ дифференциального уравнения (2.2) позволяет определить основные параметры волны, являющиеся общими для всех линейных волн, независимо от их физической природы (рис. 2.1).

 

 

 

Рис. 2.1. Геометрические параметры волны.

 

 

 

Такими параметрами являются:

амплитуда волны ;

волновое число  ;

длина волны  ;

угловая частота волны  ;

период волны ;

cкорость распространения волны ;

Сумма двух решений  (2.2)

    

                          (2.3)

    

характеризует так называемую стоячую волну, имеющую точки, в которых  достигает максимального значения, которые называются пучностями .   Решение (2.2) может быть представлено в комплексном виде:

       

                              (2.4)

    

Подстановка уравнения (2.4) в (2.2) приводит к дисперсионному соотношению:

    

 .                                  (2.5)

 

     Уравнение (2.5) может иметь конечное или бесконечное число решений, определяющих зависимость между частотой волны и волновым числом.

Каждое решение может быть записано в виде:

    

                                    (2.6)

    

Если задаться величиной , то  определяется из (2.6) и формула (2.4) может быть записана в виде:    

 

 .                              (2.7)

 

При рассмотрении двух гармонических бегущих волн

    

                                  

                                                            (2.8)

                                    

 

 в результате их суммирования получаем так называемые биения

 

    .        (2.9)

 

Если построить график функции , то получим картину, изображённую на рис. 2.

Рис. 2

Биения.

 

Волны с частотой  и волновым числом  распространяются группами. При этом скорость распространения амплитуды группы отличается от скорости распространения каждой отдельной волны. Наряду с фазовой скоростью распространения волны

   

               при                (2.10)

 

   возникает групповая скорость . Если , то фазовая и групповая скорости волны совпадают. В противном случае скорость волны зависит от ее частоты - такие волны называются диспергирующими. Общее решение волнового уравнения (2.2) получено и исследовано в ряде работ и монографий, в частности, в монографии [33]. Подробный анализ линейных трехмерных диспергирующих волн дан в монографии [34]. Там же изложена теория источников пространственных волн в сплошной среде. Аналогичные исследования линейных волн в сплошных средах в электродинамике и оптике изложены в ряде учебников, (см. например [35], [36]. Линейные волны представляют собой широкий глубоко изученный класс волновых движений.  

Можно ввести для незатухающей линейной волны аналог фазовой плоскости, а для системы волн аналог 2n-мерного фазового пространства. Введем такое пространство сначала на примере простейшей линейной синусоидальной волны, описываемой уравнением (2.1). Здесь возможны два подхода. Первый подход соответсвует введению новой системы координат - волновой

 

,                             (2.11)

 

в которой волна остаётся стационарной или меняется слабо. В этом случае

 

.                      (2.12)

 

Если мы рассмотрим, как и ранее, незатухающую волну, то в волновой системе координат она представляет собой стационарную структуру

 

 .                                    (2.13)

 

Однако пространственная бесконечномерность волны проявляется в том, что стационарная структура имеет протяженность в пространстве, задаваемую уравнением (2.12).

Другим возможным способом является введение для каждой волны трехмерного фазового пространства. Кроме функции  вводятся в рассмотрение две ее частные производные -   и  . Одномерное линейное уравнение в частных производных с постоянными коэффициентами

 

 ,                                (2.14)

 

решением которого является синусоидальная волна, распространяющаяся со скоростью , записывается в виде системы из трёх уравнений

 

                                  (2.15)

 

                                   (2.16)

 

,                                  (2.17)

где

 

                            (2.18)

 

 Если теперь построить фазовую траекторию системы (2.15) - (2.18) в трехмерном фазовом пространстве для синусоидальной волны, то получим эллипс, лежащий в плоскости, проходящей через ось  и пересекающий плоскость  под углом, тангенс наклона которого к оси  равен . Такой подход позволяет описать бесконечномерную систему одной линией в трехмерном пространстве и провести дополнительную аналогию между колебаниями и волнами (смотри рис.3).

 

 

Рис.2.3.

Фазовое трехмерное пространство одномерной волны.

 

Одна из полуосей эллипса равна максимальному значению , а другая полуось определяется как корень квадратный из суммы квадратов максимальных значений

   Выполним замену переменных:

                                        

                                                      

                                                                 (2.19)

                                                   ,

где       

                                                               (2.20)

      

   В плоскости фазовой тректории волны . Введем новую фазовую координату , определяемую соотношением

                                 

.                          (2.21)

 

Таким образом, введение новых переменых  позволяет перейти к новой плоскости , в которой фазовое описание синусоидальной волны становится эквивалентным фазовому описанию колебательного движения(смотри рис.2.4).

 

 

Рис. 2.4.

Фазовая плоскость одномерной волны в плоскости . 

 

Это описание легко может быть обобщено на случай установившихся волновых движений с постоянной скоростью и на любое конечное число волн. Построенная картина полностью аналогична фазовой картине свободных колебаний. Эта аналогия позволяет в некоторых случаях обобщать на волновые движения качественную теорию обыкновенных дифференциальных уравнений

Таким образом, линейное дифференциальное уравнение в частных производных с постоянными коэффициентами, нулевой правой частью и безграничной областью определения может быть решено в общем виде. Для него может быть получена определённая совокупность дисперсионных соотношений, характеризующих параметры линейных волн, которые являются решениями этих уравнений. Задаваясь начальными условиями, можно получить решение в виде интеграла Фурье от волновых гармоник, частота и волновое число каждой из которых удовлетворяют исследуемому волновому уравнению. При этом существенную роль начинает играть волновая дисперсия, то есть зависимость частоты волны от волнового числа [33].

Выше были рассмотрены только свободные волны. Однако, так же, как и в случае одномерных и многомерных колебаний, могут существовать и вынужденные волны. Следуя сценарию, отработанному в теории конечномерных систем, можно ввести на уровне анализа линейных и нелинейных волновых уравнений все типы резонансов, которые наблюдались у систем с конечным числом измерений.

    Дисперсионные соотношения, полученные в результате анализа дифференциального уравнения в частных производных для различных корней дисперсионного уравнения (2.5) могут оказаться близкими, так что одному волновому числу будут соответствовать близкие частоты, что может привести к появлению в функции, описывающей решение, вековых членов как по временной, так и по пространственной координатам. Возникают биения, а в предельном резонансном случае амплитуда волн линейно по временной и пространственной координатам стремится к бесконечности. Это явление также может считаться резонансным и по аналогии с резонансом в конечномерных динамических системах названо нами внутренним волновым резонансом..

    Другим типом волнового резонанса может служить вынужденный резонанс, когда в правой части волнового уравнения  стоит выражение, представляющее произведение константы на комплексную экспоненту от суммы частоты, умноженной на время и волнового числа - на координату.

В этом случае волновое движение может быть так же, как и в случае конечномерных систем, представлено в виде суммы собственных и вынужденных волн, при этом, если частотные и (или) геометрические параметры возмущающей волны окажутся совпадающими с параметрами одной из спектра возможных собственных волн системы, то амплитуда именно этой волны начнёт интенсивно расти, и возникает вынужденный волновой резонанс. Так как произвольное внешнее возмущение, распределённое в пространстве  и зависящее от времени может быть представлено в виде интеграла Фурье, то вынужденный волновой  резонанс можно искать при произвольном внешнем волновом воздействии. 

    Так же изучается волновой параметрический резонанс, когда коэффициенты волнового уравнения периодически зависят от временной и пространственной координат.

    Переход к волновым явлениям порождает идею о возможности не только колебательных временных, но и пространственных резонансов. В простейших линейных волновых уравнениях пространственная и временная координаты входят в уравнение симметрично. Следовательно, если правомочно провести сечение волнового решения по пространству и в некоторой точке рассматривать колебательное движение во времени со своими резонансными значениями искомых параметров, то с таким же успехом возможно выполнить сечение по времени и рассматривать мгновенную картину волнового движения в пространстве - построить в этом пространстве колебательную картину и, написав соответствующее дифференциальное уравнение, также искать резонансные волновые числа. Это утверждение играет конструктивную роль при анализе квазистационарных решений волновых уравнений в системе координат, связанной с движущейся волной.

    Так же, как и при исследовании конечномерных динамических систем, существенное влияние на поведение сплошных сред, описываемых волновыми уравнениями, оказывает нелинейность, которая кроме проявлений, аналогичных проявлениям, известным для  конечномерных динамических систем, имеет свой, специфический характер.

    Поэтому, прежде, чем рассматривать нелинейные волновые резонансы, рассмотрим типы нелинейности присущие волновым структурам, принципиально отличающие их от стандартных конечно-мерных динамических систем.

 

                                                       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                   Этюд 18.

 

Классификация  волн,  вихрей грибовидных и древовидных  структур и                                                                                                                                                                                                                                                                                                                                                                            транспортно-информационных  систем.

 

    Существует большое число учебников и монографий, посвящённых результатам теоретических и экспериментальных исследований волновых движений различной природы. Однако, в большинстве из них отсутствует понятие «волна». Чаще всего это понятие отождествляют с уже рассмотренными нами ранее линейными волнами. Однако, исследования последних десятилетий показали, что учёт нелинейности позволяет практически неограниченно расширить представление о волне. Наиболее общее из известных нам определений дано в монографии [33] « … в самом общем случае мы определим волну как пространственно - временную эволюцию некоторого состояния». Это определение характеризует основное свойство волны, которое остаётся неизменным независимо от типов волн, которые рассматриваются. А именно то, что при описании волновых движений мы следим не за частицами среды, в которой распространяется волна, а за параметрами или совокупностью параметров, которые описывают состояние среды. Эти параметры остаются постоянными или меняются по заданному закону в точках, которые считаются принадлежащими к волне.

    Это общее определение явилось следствием интенсивного развития за последнее время исследований нелинейных процессов в различных областях знаний и обнаружения волновых свойств у таких нелинейных процессов и структур, которые ранее не считались волновыми. В статье Ю. А. Данилова и Б. Б. Кадомцева «Что такое Синергетика», открывающей сборник [36. С. 9], говорится: «Отечественная школа нелинейных колебаний и волн, основоположником которой по праву считается Л. И. Мандельштам, рассматривает общую теорию структур в неравновесных средах как естественное развитие и обобщение на распределённые системы идей и подхода классической теории нелинейных колебаний. Ещё в тридцатых годах (прошлого века) Л.И. Мандельштам сформулировал программу создания нелинейной культуры, включающей надёжный математический аппарат и физические представления, адекватные новым задачам, нелинейную интуицию, выработанную на нелинейных задачах».

   Близкое мнение высказано в обширной монографии по нелинейной теории колебаний и волн, написанной одной из выдающихся представителей  Российской школы нелинейных колебаний П. С. Ланда [10. С.11]: «Теория колебаний и волн – это наука, изучающая колебательные и волновые движения независимо от их физической природы. Под колебательными движениями мы, согласно Л. И. Мандельштаму, будем понимать всякие происходящие длительное время ограниченные изменения состояния тела. В силу ограниченности эти изменения обязательно должны происходить туда и обратно [10]. Под волновыми движениями мы будем понимать колебательные движения, распространяющиеся в пространстве. Из этих определений видно, что изучение колебательных и волновых движений должно быть взаимосвязано, то есть разделение теории  колебаний и теории волн, как это часто делается, не является оправданным. Данное определение теории колебаний и волн является очень широким»

    Ю. А. Данилов и Б. Б. Кадомцев [37] указывают, что Л. И. Мандельштам предупреждал о ненужности на определённом этапе исследований строгих определений всех понятий в нелинейной науке. Мы полностью присоединяемся к его мнению и считаем, что в настоящее время ещё нет необходимости в абсолютно точном определении понятия «волна» (так же, как и понятий структура, система, процесс, явление, событие).

    В последние годы исследования нелинейных процессов привели к развитию новой науки  - синергетики – науки о самоорганизации материи.       Как показали многочисленные исследования, при изучении вопросов, связанных с формированием новых структур и систем, на первый план выступают их характерные волновые черты: слабая зависимость их пространственных и временных параметров от начальных условий и геометрических размеров системы.

    Такой подход позволил значительно расширить представление о волновых процессах и ввести классификацию волновых движений, структур и систем, опирающуюся на их общие волновые свойства, в рамках которой удалось проследить за характером влияния нелинейности на переход классических линейных волновых движений в динамические структуры и сложные самоорганизующиеся транспортно-информационные системы [31], [38 - 46].

Классификация проводится по трём параметрам.

1.   Классификация по типу:

а. Обобщённые волны, представляющие собой классы идентичных объектов (квантов).

б. Вероятностные волны, характеризующие изменение плотности вероятности отыскания системы или структуры в одном из возможных для неё состояний из континуума возможных состояний системы.

в. Классические волны в сплошной среде, характеризующие изменение во времени и пространстве плотности какого-либо параметра или связанной между собой совокупности параметров сплошной среды.

2. Классификация по характеру взаимодействия с другими системами, аналогичная рассмотренной нами ранее классификации конечномерных динамических систем:

а. Свободные (собственные) волны.

б. Вынужденные волны.

в. Автоволны.

3. Классификация по степени нелинейности [31, 39, 41, 45, 46].

а. В качестве первого класса рассматриваются все волны относительно малой амплитуды, математическое описание которых в одномерном случае кратко представлено выше в виде совокупности решений линейных волновых уравнений в частных производных.

б. Ко второму классу, названному нами умеренно - нелинейными волнами, отнесены различные формы ударных волн в сплошных средах, солитоны, а также скачки тех или иных параметров в однородной среде и границы раздела сред. В качестве подкласса данного класса могут быть рассмотрены автоволны в активных средах [47], диссипативные континуальные структуры и структуры, формируемые в результате возникновения режимов с обострением [48]. Умеренно-нелинейные волны часто являются границами некоторых объёмов, которые они отделяют от окружающей среды – поля. Такие объёмы мы будем называть телами-волнами.

в. К третьему классу, названному нами вихревыми ударными  волнами, отнесены вихревые и (или) спиральные структуры, формируемые вследствие пространственной потери устойчивости фронта и формы умеренно нелинейных волн. В частности, сюда относятся специфические автоволновые образования, называемые ревербераторами [47].  

г. К четвёртому классу, названному грибовидными структурами, отнесены структуры мультипольной природы, формирующиеся из вихревых и спиральных структур. Различные модификации и комбинации структур такого типа составляют основу практически всех объектов живой и неживой природы.

д. К пятому классу отнесены структуры, названные нами древовидными, геометрия и бифуркационная динамика которых может быть описана методами математической теории графов, в частности, теории математических деревьев [49].

е. К шестому классу мы отнесли сложные, в том числе самоорганизующиеся системы, названные транспортно - информационными, и являющиеся, в основном, результатом трансформации и взаимодействия грибовидных и древовидных структур, а также волновых движений и структур более низких классов.

    Несмотря на то, что четвёртый, пятый и шестой классы структур и систем встречаются и в неживой природе, наиболее широко они распространены в технических, биологических и социальных системах. Поэтому общие закономерности их динамики оказываются важными не только для физики и химии, но и, главным образом, для технических приложений, наук о Земле, биологии и наук о человеке и обществе.

     Рассмотрим объекты предложенной классификации несколько более подробно.

 

 

                                                          

 

 

                                                           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                            

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                Этюд 19.

 

 Умеренно - нелинейные волны.

 

Некоторым линейным волновым уравнениям можно сопоставить соответствующие нелинейные уравнения. В качестве примера вновь, следуя [33], рассмотрим одномерные уравнения первого порядка.

                     Простейшие линейные уравнения. I класс:

                  a)              

                             

  b)                       (2.22)

 

                  c)      

Соответствующие им нелинейные уравнения. II класс:

 

                  a)  -           уравнение Пуассона-Римана;

                                                      

                  b)- уравнение Бюргерса;              (2.23)

                    

                  с)   - уравнение Кортевега-Де-Фриза.

 

Если уравнение (2.22 a) описывает произвольную стационарную волну, то уравнение (2.23 а) [33] , например, при начальных условиях:

    

                                (2.24)

 имеет решение :

 

                ,                        (2.25)

где  пространственная координата, движущаяся со скоростью  (которая в свою очередь сама является функцией от  и ). Eсли функция  имеет производную  при  в точке , то

 

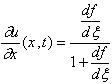          .                              (2.26)

Если , то  бесконечна при  . Нелинейность приводит к деформации волнового профиля, возрастающей с ростом . Если  , то решение уравнения (2.23а) становится многозначным. Физически это приводит к появлению в сплошной среде движущихся разрывов. Такие типы движений в механике сплошной среды называются простыми волнами. Подробное исследование разрывов в трёхмерной сплошной среде было выполнено в работах Ж.Адамара, Н.Е.Кочина, К.Трусделла [50-52] и других авторов, в которых рассмотрена классификация и изложены общие свойства сингулярных поверхностей - поверхностей разрыва.

В общем виде уравнение движения сплошной среды имеет вид:

 

                                    (2.27 )

 

 где  - радиус-вектор материальной точки в абсолютной системе координат; -вектор лагранжевых координат точек сплошной среды. Тогда поверхность в отсчётной конфигурации или её образ в текущей конфигурации движущегося тела называется сингулярной поверхностью (или волной) -го порядка, если она сингулярна по отношению к некоторой -ой производной скалярного, векторного или тензорного поля  (то есть на этой поверхности функция или её производная, описывающие поле, терпят скачок), определяемого в пространстве, занятом сплошной средой. Cингулярные поверхности порядков 0 и 1 называются сильными: к ним относятся  математические абстракции типа классических ударных волн нулевой толщины, бесконечно тонких вихревых пелен, о формировании которых мы будем говорить позднее, разрывы и поверхности контакта двух тел, фазовые границы. Сингулярные поверхности порядка 2 и выше называются слабыми. Фактически к сингулярным поверхностям относятся любые скачки параметров в сплошной среде, любые процессы, связанные с фазовыми переходами в сплошных средах. При этом локально в направлении, нормальном к сингулярной поверхности, параметр, терпящий скачок, удовлетворяет нелинейному уравнению типа:

 

,                          (2.28)

 

где  - проекция градиента величины  на нормаль к сингулярной поверхности. В обшем случае может быть произвольной функцией, в том числе, равной нулю или константе. Уравнение (2.28)  может быть заменено локально любым из уравнений (2.23b)-(2.23c) или их обобщений [33, 47, 48]. Тем самым, объединяя путём сращивания различные типы внутренних одномерных нелинейных волн с внешним анализом сингулярных поверхностей в сплошной среде и предлагая конструктивный способ изучения зон резких изменений в сплошной среде, мы тем самым можем ввести в рассмотрение наряду с классом линейных волновых движений, новый широкий класс нелинейных волновых структур, которые могут быть названы нелинейными обобщенными ударными волнами или умеренно-нелинейными волнами.

Поясним возможный алгоритм асимптотического анализа нелинейных обобщённых ударных волн. Если в сплошной среде формируется или имеется не скачок, а зона резкого перехода от одного значения параметра к другому, ширина которой значительно меньше радиуса кривизны этой зоны, то перемещение свойств среды вблизи этой зоны можно назвать трехмерной ударной волной. Все соотношения, полученные для сингулярных поверхностей, в первом приближении оказываются справедливыми и для этого случая. При этом для анализа поля вблизи зоны резкого скачка параметров в ряде случаев локально оказывается справедливым нелинейное уравнение, являющееся обобщением уравнения Бюргерса, которое может быть переписано в форме

    

                           (2.29)

 

Особенность уравнения (2.29) заключается в том, что оно может иметь несингулярное стационарное решение, которое, например, в случае  имеет вид.

 

                                          (2.30)

 

                             (2.31)

                                                          

   Здесь  определяются из решения внешней задачи в приближении сингулярных поверхностей

 

                                                     (2.32)

 

   На языке аэродинамики полученное решение описывает структуру ударной волны. Главный вывод, сделанный для одномерного движения и являющийся, как следует из предыдущего анализа, общим, состоит в следующем [33]: "Нелинейность уравнения Бюргерса позволяет гладко соединить два асимптотически однородных состояния (разрыв) c помощью непрерывно изменяющихся состояний. Член второго порядка стремится нейтрализовать влияние нелинейности в области, где возможно появление сингулярности, и сгладить разрывы."

    Если , мы вновь возвращаемся к сингулярным поверхностям.

Замена переменных позволяет линеаризовать уравнение Бюргерса и свести его к линейному уравнению теплопроводности, что позволяет изучать взаимодействие нелинейных ударных волн [10]. 

    Сочетание в волновых уравнениях членов, определяющих дисперсию, с нелинейными членами порождает наряду с обычными волнами удивительные объекты - уединённые волны или солитоны, открытие которых имеет почти двухвековую драматическую историю, и не все свойства которых изучены полностью.

« … в реальных системах спустя некоторое время устанавливаются и довольно долго существуют волны, по форме близкие к солитонам. В дальнейшем эти волны медленно затухают. Красочное описание образования такой волны в воде перед остановившейся внезапно баржой и последующего её поведения дал Джон Скотт Рассел [53-54], который наблюдал это явление ещё в 1834 г.: «Я следил за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась; вместо этого она собралась около носа судна в состоянии бешеного движения, затем неожиданно оставила его позади, катясь вперёд с огромной скоростью и принимая форму большого одиночного возвышения, т. е. округлого, гладкого и чётко выраженного водяного холма, который продолжал свой путь вдоль канала, нисколько не меняя своей формы и не снижая скорости. Я последовал за ним верхом, и когда я нагнал его, он по-прежнему катился вперед со скоростью приблизительно восемь или девять миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от фута до фута с половиной. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала.»[10]

    Солитоны обладают многими свойствами, которые до их открытия приписывались частицам. Одновременно их можно считать специфическими размытыми ударными волнами. Солитоны появляются как устойчивые  решения различных дифференциальных уравнений, описывающих, казалось бы, не связанные между собой явления природы. В их формировании и их свойствах есть нечто загадочное, что привлекло к их исследованию крупнейших учёных [10], [33].

    Можно считать, что при формировании солитонов проявляется специфическая форма нелинейного резонанса между членами дифференциального уравнения, которое их описывает: дисперсионные члены вызывают расхождение в пространстве диспергирующих волн с различными волновыми числами, тогда как нелинейность приводит при определённых условиях к концентрации в одной точке максимумов волн различной частоты. Эти два эффекта уравновешиваются в солитоне и формируют устойчивую структуру, переносимую в пространстве с постоянной скоростью практически без изменения её формы

Динамика солитона, в частности, описывается уравнением Кортевега-де-Фриза рядом его аналогов  [33, 55-65]. Вслед за [33] выпишем одно из стационарных решений уравнения (2.23с)

 

 ,                           (2.33)

 

   где

 

                                       (2.34)

 

                                  (2.35)

 

а -эллиптические функции Якоби (-функция,обратная к ).

 -вещественные корни уравнения

 

                                   (2.36)

 

A и B-постоянные интегрирования, определяемые условиями на бесконечности.

Функция , описываемая уравнением (2.33), является периодической нелинейной волной с периодом

 

 ,                                  (2.37)

 

где -полный эллиптический интеграл первого рода:

 

                                .

 

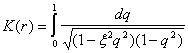   Из-за наличия функции  в выражении (2.33)  нелинейная волна, описываемая этой формулой, называется кноидальной. Если , то формула (2.33) принимает следующий вид

 

                                (2.38)

 

                                            (2.39)

 

   Период волны, описываeмой равенствами (2.38) и (2.39), оказывается равным бесконечности.

   Устремляя    к ,получаем:

 

                                             (2.40)

 

   и окончательно:

    

                (2.41)

 

   Уравнение (2.41) - уравнение уединённой волны-солитона. Обнаруженные экспериментально Скоттом Расселлом (1844) [53-54]. и исследованные математически Кордевегом и Де Фризом [55], солитоны долгое время не привлекали внимания исследователей, пока в 50-х, 60-х годах аналогичное уравнение не было обнаружено при исследовании плазмы [56]. Затем поток исследований солитонных решений различных нелинейных уравнений возрастает вплоть до настоящего времени экспоненциально [57-65]. Подробный список работ, посвящённых исследованию солитонных решений различных уравнений имеется в [10],[63],[64].

Если рассмотреть солитонное решение уравнения Кортевега-Де-Фриза как первый член внутреннего разложения какого-либо трёхмерного разрывного движения, как это мы сделали ранее для ударных волн, то при асимптотическом анализе внешнего решения можно рассматривать такую структуру как частный случай сингулярной поверхности минус первого порядка, то есть как особую форму слияния двух близко расположенных скачков. Качественно аналогичный результат можно получить, если при анализе ударных волн рассматривать не саму функцию, а её производную по нормали к фронту волны. Таким образом, солитонное решение может быть естественным образом включено во введённый нами класс обобщённых ударных волн как нелинейная ударная волна минус первого порядка (так же как и режимы с обострением, хотя  характер локального поведения основной меры в районе обострения существенно отличается).

    Между поведением решений уравнений типа Кортевега-де-Фриза и типа Бюргерса имеется принципиальное различие, определяемое порядком высшей производной и связанное с диссипацией энергии волн. Однако, это отличие не столь велико, чтобы воспрепятствовать включить все рассмотренные выше и аналогичные им нелинейные волны в один класс. Существуют волновые движения, являющиеся переходными от линейных синусоидальных волн к волновым структурам второго класса (например, кноидальные волны).

Сингулярные границы, обобщение которых в виде умеренно нелинейных волн дано выше, обычно представляют собой замкнутые поверхности, отделяющие внутреннюю часть пространства от остального мира. Эта замкнутая часть пространства может быть названа телом-волной. Большинство предметов окружающего мира может быть отнесено именно к этому классу..

    Таким образом, специфическими особенностями, существенно отличающими их от соответствующих решений систем обыкновенных уравнений, могут обладать решения некоторых нелинейных уравнений в частных производных, порождающих совершенно новые явления, связанные с зависимостью искомых параметров движения от пространственной координаты. Нелинейные члены типа произведения некоторой функции искомой величины (или совокупности искомых величин) на её производную по пространственной координате порождают во взаимодействии с линейными и нелинейными членами уравнений, описывающими дисперсию и диффузию, такие новые структуры и явления  как ударные волны, солитоны, автоволны, диссипативные структуры, режимы с обострением. Появление ударных волн физически означает формирование в сплошной среде движущихся разрывов, что является проявлением одного из важнейших нелинейных механизмов рождения границ в сплошной среде. Наличие процессов такого типа  позволяет рассматривать резкие  и размытые скачки параметров в сплошных средах как обобщённые ударные волны и относить их также ко второму классу – умеренно - нелинейным волновым системам.

    Уравнения теплопроводности и Бюргерса представляют простейший пример класса параболических дифференциальных уравнений в частных производных, описывающих широкий круг процессов: и образование турбулентности, и химическую кинетику в условиях конвекции, и распространение волн в активных средах…

В одномерном случае общий вид этих уравнений запишется следующим  образом:

.                      (2.42)

В некоторых случаях нелинейности, определяемые неоднородностью среды, в которой формируются нелинейные волны, или её активностью, порождают в среде процессы, приводящие к неограниченному росту параметров возмущения. Иногда этот рост значительно более интенсивен, чем рост возмущений при исследовании экспоненциальной неустойчивости динамических систем. Такие явления С.П. Курдюмов назвал режимами с обострением [48]. Хотя эти режимы и существенно отличаются от ударных волн и солитонов, однако, по нашему мнению, их также можно отнести к умеренно- нелинейным волнам.

    Скорость перемещения умеренно - нелинейных волн так же, как и  линейных, может меняться в широких пределах. Так, например, если умеренно-нелинейная волна является границей неподвижного твёрдого тела, то её скорость равна нулю. В этом случае граница является замкнутой. Она отделяет внутренность тела от внешней среды – поля.

 Совокупность умеренно-нелинейной волны и объёма, отделённого ею от окружающего пространства, будем называть телом-волной.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Этюд 20

 

 Вихревые и грибовидные структуры.

Транспортно-информационные системы.

 

 

1. Вихревые ударные волны первого рода. Формирование вихревых пузырей. Ревербераторы.

 

Условия формирования следующего класса нелинейных волновых структур определяется, главным образом, особенностями взаимодействия умеренно - нелинейных волн со средой, их окружающей. Частным примером такого взаимодействия являются поверхностные волны на границе раздела сред. Классические линейные волны на поверхности воды являются результатом взаимодействия границы раздела (умеренно-нелинейной волны) с жидкостью, подверженной действию сил тяжести. Как известно, на границе раздела сред возникают волновые деформации, в первом приближении представляющие собой двумерные диспергирующие линейные волны. Изучению этих волн в настоящее время посвящена обширная литература, например [34], [65-67]. Увеличение энергии гравитационных волн на поверхности воды приводит к появлению существенных нелинейных эффектов, связанных с взаимодействием границы со средой.

Это нелинейное взаимодействие подробно изучено математически. Выполненные исследования [65 - 67] показывают, что на свободной поверхности могут реализовываться, в зависимости от относительной глубины погружения, вычисленной по длине волны, два типа симметричных нелинейных волн: при малых глубинах водоёма - кноидальные и уединённые волны солитонного типа, а при значительных глубинах - волны Стокса. Несмотря на различие этих двух типов волн, между ними имеется много общего, связанного с нелинейностью:

    а) происходит выполаживание подошвы и заострение вершины волны, при этом профиль волны в случае больших глубин водоёма с увеличением амплитуды стремится к форме предельной волны Стокса с угловой критической точкой в вершине [65], что приводит к качественно новым бифуркационным явлениям;

    б) на свободной поверхности увеличивается модуль абсолютной скорости частиц жидкости (у предельной волны Стокса в критической точке скорость жидкости становится равной скорости перемещения волны).

     Тем самым, на границе между жидкостью и газом наряду со скачком плотности возникает и становится всё более интенсивным скачок завихрённости.

    Cвязь между нормальной и касательной составляющими вектора, параметры которого определяют свойства сингулярной поверхности, описывается соответствующими интегральными уравнениями, ядрами которых являются фундаментальные решения уравнений математической физики для среды, формирующей тело-волну. Нелинейность волн деформации границ раздела сред наряду с умеренно-нелинейными волнами приводит к появлению нового типа волновой картины: Стоксовой волны с угловой точкой, - появляется возможность принципиально новой геометрической трансформации границы - потеря аналитичности её формы, появление угла - излома фронта волны.

Аналогичные особенности (каустики) [34], [68] появляются и при пространственном анализе фронтов классических линейных волн, однако там они обычно не сопровождаются скачками завихрённости и формированием спиральных структур, составляющими основные особенности процессов, которые будут изучаться нами ниже. Теория каустик волновых фронтов в настоящее время интенсивно изучается физиками и математиками. Она оказывается тесно связанной с теорией особенностей лагранжевых многообразий и теорией катастроф [68].

Итак, основным следствием нелинейных взаимодействий, приводящих к формированию следующего класса волновых структур, является порождение на волновых фронтах интенсивной завихрённости, распределение которой в пространстве или на плоскости приводит к существенным нелинейным эффектам и порождает новые  структуры, которые начинают жить по собственным законам, взаимодействуя с породившей их средой. К этому же классу могут быть отнесены и структуры, которые представляют зоны концентрации ротора любого вектора, не обязательно вектора скорости сплошной среды.

Порождение и диффузия завихрённости, наиболее интенсивно проявляющиеся на контактных поверхностях, отнесённых нами к умеренно нелинейным волнам, значительно усложняет их структуру, формирует новые типы обобщённых ударных волн: пограничные слои резких градиентов касательных составляющих вектора, Существенно нелинейный характер вихревых волн, скорость перемещения которых может совпадать со скоростью перемещения среды, в которой они возникают (то есть собственная скорость может стать равной нулю), приводит к возникновению нового класса нелинейных вихревых структур, которые, сохраняя свойства породивших их классических линейных и умеренно - нелинейных волн, оказываются значительно ближе к телу-волне, то есть формируют устойчивые слабодеформируемые структуры, переносящие не только свою форму, но и большую часть массы среды, в которой они формируются.

Проанализируем возможные пути формирования и основные топологические свойства вихревых (или в более общем случае - роторных) структур. Если в качестве модели рассмотреть линейные поверхностные волны на границе раздела двух сред и рассчитать в рамках допущений  невязкой жидкости скачок касательных скоростей, то этот скачок, хотя и существует, но очень мал. С увеличением нелинейности интенсивность сдвигового слоя растёт. Предельная Стоксова волна уже в значительной степени вихревая. Вблизи критической точки (вершины)  интенсивность завихрённости максимальна. Дальнейшее развитие влияния нелинейности на характеристики  поверхностных волн происходит по другим законам - законам вихревых ударных волновых структур.

В работе [38] одним из авторов совместно с Н. Ю. Завадовским рассмотрена простейшая модельная задача, решение которой вскрывает механизм развития на границе раздела сред новых вихре - волновых структур и объясняет качественно один из элементов сложного нелинейного явления - спирализации нелинейных волн на границе раздела сред. Если проанализировать, при допущении о пренебрежении нормальными к границе скоростями по отношению к касательным, поведение свободной первоначально гладким образом искривленной границы раздела сред без учета действия сил тяжести, то математическая постановка такой задачи для невязкой жидкости постоянной плотности сводится к уравнению Лапласа внутри жидкости и к уравнению Пуассона-Римана (2.23 а) для скачка касательных скоростей на деформируемой границе раздела.

Совместное рассмотрение этих связанных между собой уравнений приводит к аналитическому решению, форма которого показывает, что на свободной границе через конечный промежуток времени формируется продольная поверхностная ударная волна - появляется отсутствовавший ранее скачок продольных касательных скоростей - что приводит к скручиванию самой границы в двойной спиральный вихрь с бесконечным числом витков [69 - 72] (рис.3.1)

 

 

Рис.3.1

 Формирование двойного спирального вихря.

   

    Удалось построить стационарные двумерные течения идеальной жидкости, которые можно классифицировать как обобщения двойного спирального вихря. Если ввести при рассмотрении двумерных потенциальных потоков с границей следующие комплексные функции:

 

 

                  (2.43)

 

и рассмотреть стационарное течение, а затем определить уравнение связи

                

                                      (2.44)

    

то получим спектр течений, представляющих потоки вблизи угловых точек, либо внутри двойных спиральных вихрей. Примеры таких  структур представлены на рис. 3.2.

 

 

Рис.3.2

 

Различные типы вихревых ударных волн первого рода

 

 

В действительности, однако, так же как и в случае ударных волн, происходит диффузионное и хаотическое размывание как в касательном, так и в нормальном направлении указанных идеальных структур, наиболее интенсивноe внутри центральных областей спиралей.

Совокупность формирующихся, стационарных и диссипирующих структур этого типа названа нами вихревыми ударными волнами первого рода. Они обычно являются элементами таких сложных физических явлений, как разгонные вихри за крылом, отрывные пузыри на телах, концевые вихри на крыльях, дорожки Кармановских вихрей за плохообтекаемыми телами и паровыми и газовыми кавернами и т. д.

Если рассматривать подобные структуры с топологической точки зрения и учесть диффузию завихрённости при их формировании, то их скорее можно считать телами - волнами, чем умеренно-нелинейными волнами, хотя формируются они в районе фронтов умеренно-нелинейных волн. Именно формирование из умеренно-нелинейных волн вихревых ударных волновых структур первого рода и является тем качественным скачком, который позволяет выделить третий класс - нелинейные вихре -волновые и спиральные  структуры - вихревые ударные волны первого рода.

Если размеры введенных ранее в рассмотрение тел - волн определяются параметрами их границ, то вихревые ударные волны первого рода фактически являются одновременно и частью границы какого-либо другого тела - волны,  и сами по себе вновь сформировавшимися из этой границы телами - волнами. Главной их особенностью как вихревых структур является наличие на какой - либо из стадий их формирования спиральных волн.

К этому же классу могут быть отнесены ревербераторы [47. C. 129, которые могут быть названы спиральными авто - волнами.

 

2.                                                                                                                                                                                                             Вихревые ударные волны второго рода. Вихревые пелены.

 

Анализ топологических свойств линий и поверхностей обусловливает еще один вид формирования вихре - волновых структур - самопересечение фронтов умеренно нелинейных волн. Самопересечение фронтов приводит к различным последствиям у гамильтоновых (линейные волны и солитоны)  и диссипативных структур (ударные волны, границы раздела фаз, автоволны ).

Если в первом случае возможно формирование особенностей, соответствующие катастрофам Тома - Арнольда [68] (каустики), то во втором - может возникнуть новое явление. Фронт обобщенной умеренно-нелинейной волны, рассматриваемый в первом приближении извне как двумерная поверхность, может деформироваться таким образом, что в какой-то  момент времени две различные точки границы (обобщенной ударной волны) окажутся в одной точке пространства - происходит слипание границ [73].

Разрыв твердых тел, радиоактивный распад и слияние ядер атомов, образование капель, формирование брызг, появление трещин, стягивание объёмов нефти при её откачке, землетрясения - представляют собой физическую интерпретацию описанного выше процесса. Биологическими интерпретациями того же явления могут служить слияние и деление клеток, рождение нового организма. Примером проявления этого механизма в социальных процессах может служить формирование и разрушение империй, слияние корпораций.

 В качестве одного из последствий такого совмещения в пространстве различных частей границы можно предположить превращение точки соприкосновения в линию (в двумерном случае) (рис.3.3)

 

 

 

 

Рис.3.3

 

Формирование вихревой ударной волны второго рода.

 

 

или поверхность - в трёхмерном,- сдвоенной границы. Формирование сдвоенных границ и их перемещение в сплошной среде может сопровождаться образованием вихревой ударной волны второго рода нулевого или первого порядка в терминологии К.Трусделла - вихревой пелены.

В большинстве практически важных случаев появление вихревых ударных волн первого рода сопровождается пересечением и слипанием границ и фронтов и отделением сформировавшегося вихревого объема от остальной части границы.

Гидродинамическими примерами таких явлений можно считать обтекание крыла конечного размаха, течение около плохо обтекаемых тел, обтекание ниш и отверстий, кавитационные течения и т. д.

Процесс разрушения фронтов умеренно-нелинейных волн может происходить и несколько иным способом. Этот способ связан с множественным перезамыканием границ и появлением тел-волн малых масштабов в районе разрушения.

Физическими примерами таких явлений могут служить

а) образование на поверхности разрушающихся волн брызговой струи, состоящей из множества капель;

б) образование пузырьковой кавитации на поверхности движущихся в жидкости тел при высоких скоростях движения;

в) формирование лавин, сходящих со склонов гор;

д) формирование кучи песка.

Последний пример, в теоретическом исследовании которого вновь, как и при исследовании многих других нелинейных явлений, появились степенные функции, стал математической моделью для построения теории самоорганизованной критичности, оказавшейся полезной моделью при исследовании транспортно-информационных систем (см., например,[74]).

 Можно высказать гипотезу, что явление диссипации в макропроцессах является следствием формирования вихревых ударных волн первого и второго рода на микроуровне и наноуровне. Аналогичная гипотеза может быть высказана  и о возможной природе вязких потерь энергии при турбулентности.

 

3.   Грибовидные структуры.

 

Одним из возможных следствий возникновения вихревых ударных волн первого и второго рода является появление трехмерных структур, называемых в настоящее время  грибовидными.

Характерным примером возникновения вихревых ударных волн  первого и второго рода и формирования грибовидной структуры является процесс образования циркуляционного течения около движущегося в жидкости крыла конечного размаха.

С изложенных выше позиций крыло может рассматриваться как тело - волна, а его граница как обобщенная присоединенная к телу нелинейная ударная волна, движение которой создает в жидкости поле скоростей и давлений, перемещающихся относительно частиц жидкости со скоростью, равной скорости движения тела.

Вблизи границы тела - волны наряду со скачком плотности параметра, переносимого этой волной, обычно формируется также волна резкого скачка касательных скоростей (вихревой пограничный слой). На границе движущегося тела имеются, как минимум, две критические точки, т. е. точки, в которых скорость жидкости в незавихренной области близка к скорости движения тела, и наблюдаются максимальные продольные градиенты завихрённости.

 Если провести вполне уместную аналогию с фазовым пространством конечномерной динамической системы, то критические точки около движущегося крыла во многом окажутся аналогичными седловым точкам сепаратрисы фазового пространства. И так же, как вблизи седловых точек сепаратрисы фазового пространства конечномерной динамической системы возможно появление бифуркации рождения цикла [16, 75], вблизи критических точек потока может сформироваться вихревая ударная волна первого рода, которая затем отделяется от поверхности крыла, формируя вихревую пелену-вихревую ударную волну второго рода. Автомодельным аналогом этого явления служит формирование ревербератора при огибании препятствия автоволнами со скачком нормальных скоростей [47]).

Появление вихревых ударных волн тем более вероятно, чем ближе критическая точка к уже заданной самой формой профиля крыла вихревой ударной волне первого рода в виде острой задней кромки с заданным скачком наклона касательной к поверхности крыла.

Указанная аналогия может быть обоснована следующими рассуждениями, которым можно придать строгую математическую форму [76]. В частном случае изучения динамики человеческой популяции это было сделано в нашей монографии [45].

Динамика сплошной среды описывается, как минимум, двумя типами дифференциальных уравнений: системой нелинейных уравнений в частных производных для определения зависимости вектора скорости от координат пространства (уравнениями неразрывности, сохранения количества движения и энергии), и системой обыкновенных дифференциальных уравнений для определения траекторий частиц сплошной среды, отражающих тот факт, что скорость есть производная от радиуса - вектора траектории по времени. Если решение первой системы уравнений получено, то в результате подстановки его во вторую систему получим систему обыкновенных дифференциальных уравнений с размерностью, равной размерности пространства, фазовые траектории которых есть траектории частиц сплошной среды. Это условие активно используется в теории динамических систем. Однако, обычно характер фазового пространства определяется заранее заданным типом правых частей обыкновенных дифференциальных уравнений и получающиеся при этом фазовые потоки редко соответствуют каким-либо реальным течениям сплошной среды. Можно поставить обратную задачу - строить и классифицировать типы и особенности обыкновенных дифференциальных уравнений по типам уравнений и особенностей динамики сплошной среды, которым они соответствуют. Такой подход, во-первых, обосновывает частичное подобие структур, формируемых в сплошной среде особенностям и аттракторам фазового пространства стандартных динамических систем, а во-вторых позволяет сопоставлять специфические структуры, формирующиеся в сплошной среде, например, структуры, классификация которых приводится здесь, с особыми точками, аттракторами и репеллерами фазового пространства систем специфических (нестандартных) обыкновенных дифференциальных уравнений. Так, например, любому обыкновенному дифференциальному уравнению первого порядка с одной переменной путём комплексификации может быть сопоставлено некоторое течение идеальной несжимаемой жидкости и наоборот, всякому течению идеальной жидкости могут быть сопоставлены сначала одно комплексное.  а затем одно или два связанных дифференциальных уравнения [76].  

Продолжим качественный анализ динамики потока около крыла. Вблизи критических точек так же, как и вблизи точек слома границы, наблюдаются максимальные продольные градиенты завихренности и появляются условия для возникновения спиральных вихревых ударных волн первого рода. Наиболее интенсивно этот процесс происходит вблизи критической точки, расположенной около задней острой кромки крыла, около которой как сами величины интенсивности завихрённости, так и её градиенты максимальны.

Утолщение пограничного слоя в этом районе создает условия для формирования между задней кромкой крыла и расположенной над ней критической точкой спиральной вихревой структуры - вихревой ударной волны первого рода, математический анализ автомодельного формирования которой выполнен в ряде работ (см. например, [77]). Диффузия завихрённости и внутренние потери устойчивости вихревой поверхности приводят к формированию вихревого пузыря. Взаимодействуя c потоком около крыла, вихревой пузырь формирует течение, приводящее к самопересечению вихревых слоев и образованию вихревой пелены - вихревой ударной волны второго рода, возникновение и рост которой отделяет вихревой пузырь от крыла.

 

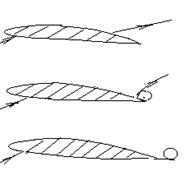
Рис.3.4

 

Формирование вихревых ударных волн первого и второго рода при обтекании задней кромки крыла.

 

При этом вблизи боковых кромок крыла конечного размаха вихревая пелена окаймляется постоянно формирующимися вихревыми ударными волнами первого рода (концевыми вихрями). Возникает одна из форм пространственной вихревой структуры, названная нами грибовидной.

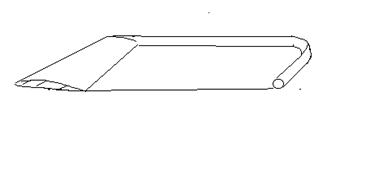
                                                            Рис.3.5

 

 

Течение около крыла конечного размаха как нейтральная грибовидная структура.

 

Возникшая структура достаточно сложна, так как включает в себя вихревые ударные волны первого и второго рода, а также присоединенную к движущемуся телу обобщенную ударную волну - границу тела. Элементы такой грибовидной структуры движутся с существенно различными скоростями и вследствие этого её продольный размер интенсивно растёт во времени.

 Мгновенно изменив угол атаки крыла до нуля, мы можем получить вихревое кольцо с перемычкой, которое является одной из наиболее простых форм свободных грибовидных структур (рис.3.6)

Рис. 3.6

Свободная нейтральная грибовидная структура.

 

Возникшая свободная грибовидная структура может трансформироваться и тем самым влиять на движение окружающей её сплошной среды.

    Рассмотренный тип грибовидной структуры может быть назван нейтральным. Топологически возможны грибовидные структуры еще двух типов. Грибовидные структуры "женского" типа, представителями которых являются вязкие струи, вытекающие из отверстий в среду, совпадающую со средой струи. В этом случае происходит существенная трансформация вихревой пелены, которая, оставаясь сдвоенной поверхностью, соединяется с обобщенной ударной волной (границей), породившей грибовидную структуру. Вихревая пелена преобразуется в "ножку" грибовидной структуры.

Рис.3.7

Грибовидная структура открытого типа.

 

В отличие от нее, например, струя жидкости, вытекающая в воздух, представляет собой пример замкнутой ("мужской") грибовидной структуры, формирующейся на основании имевшейся ранее границы раздела сред.

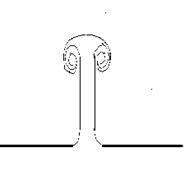
Рис.3.8.

 Грибовидная структура замкнутого типа .

 

 Наиболее характерным примером замкнутой грибовидной структуры является осесимметричная картина отрывного обтекания шара.   Грибовидные структуры в последние годы начали интенсивно изучаться  как экспериментально, так и теоретически [78]. Решения ряда  вихревых и струйных задач гидродинамики являются адекватными моделями для их описания.

    Простейшим примером гидродинамического, и не только гидродинамического, описания является особенность типа концентрированного в точке диполя.  Как следует из предыдущих рассуждений, эта модель может также считаться характерной особенностью фазового пространства соответствующего обыкновенного дифференциального уравнения, что  позволяет включить вихревые и дипольные особенности наряду с вихревыми ударными волнами в число основных сингулярностей обыкновенных дифференциальных уравнений нестандартного типа.

    В двумерном случае грибовидная структура может быть приближённо смоделирована парой равных симметрично расположенных концентрированных вихрей. Решение подобной задачи, впервые полученное Кельвином, можно найти в любом учебнике по гидродинамике. Если подойти к рассмотрению этого решения с позиций качественной теории структур и бифуркаций фазового пространства обыкновенных дифференциальных уравнений, то можно увидеть в ней характерные особенности, являющиеся, по-видимому, особенностями всех грибовидных структур.

    Можно рассматривать две различные задачи.

1.   Свободное движение вихрей, когда скорость их перемещения равна средней скорости движения идеальной жидкости вблизи вихря.

2.   Вынужденное движение вихрей, когда скорость перемещения «присоединённого вихря» задаётся.

    Первая задача является специфическим резонансным вариантом второй, при этом резонансным условием является равенство задаваемой скорости перемещения пары вихрей и среднего вектора скорости жидкости в районе их расположения. Это условие является частным случаем обнаруженного нами класса явлений, который может быть назван вихре - волновым и структурным резонансом .

    Основным безразмерным параметром, определяющим бифуркационные характеристики рассматриваемой структуры при решении второй задачи, является отношение циркуляции вихря к скорости движения вихревой пары (или скорости набегающего потока) и к расстоянию между вихрями. При изменении этого параметра вид замкнутой области, формируемой течением около вихрей, проходит несколько качественных бифуркаций [79].

    Этой структуре соответствуют три присоединённые волны. Тело – волна, формируемая сепаратрисой соответствующего гидродинамического течения, отделяющей внешнее течение от внутреннего, максимальный  размер которого, измеренный в направлении движения, может быть принят за длину волны, а скорость которого определяется скоростью перемещения системы вихрей. Отсюда определяется частота этой волны.

    Другой волной является дипольная структура, амплитудой которой может считаться интенсивность диполя, равная произведению циркуляции вихря на расстояние между вихрями. Частотой этой волны можно считать отношение интенсивности вихря к квадрату расстояния между вихрями, а длиной волны – само это расстояние. Скорость волны может быть определена как циркуляция вихря, делённая на число 2 пи и расстояние между вихрями. В резонансном случае  скорости обеих волн совпадают.

    Эта простая модель может быть применена для описания грибовидных структур всех типов.

Однако, реальные грибовидные структуры обладают ещё одним свойством, не отражаемым рассмотренной выше схемой.

Это свойство наиболее характерно для открытых грибовидных структур.

Оно состоит в обмене веществом с окружающей средой, в наиболее общем случае проявляемом в захвате массы окружающей среды, её переработке путем включения во внутренний циркуляционный поток и возвращение ранее захваченной массы в окружающую среду. Простейшими моделями такого движения являются модель идеального гидравлического  движителя [80] и модель спутной  струи за обтекаемым телом.[110]

    Наиболее широко распространены грибовидные и являющиеся результатом их трансформации дипольные структуры в биологических и социальных объектах, где они принимают различные специфические формы. Их длительное существование обеспечивается в этом случае  внутренней энергией активной среды, в которой они формируются. По аналогии с автоволнами они могут быть названы автогрибовидными структурами. Все живые существа и многие автономные органы живых организмов можно отнести к грибовидным структурам.

    Если ещё раз обратиться к аналогии с обыкновенными дифференциальными уравнениями обычного типа, то аналогами грибовидных структур в некоторой степени могут считаться двумерные торы.

 

 

4. Возможные способы качественной трансформации грибовидных структур.

Древовидные структуры.

 

Благодаря достаточной сложности грибовидных структур может наблюдаться значительное разнообразие топологических форм их трансформации, приводящие к бифуркационным изменениям этих структур.

Рассмотрим на качественном уровне некоторые потенциально возможные типы трансформации грибовидных структур, приводящие к их изменениям и появлению новых:

    а) В первой топологической форме (нейтральной) вихревая пелена благодаря вращательному движению среды вокруг замкнутой вихревой ударной волны первого рода, наматывается на неё и пополняет её завихрённость, а кроме того уходит по нормали от вихревого объёма  на определённое расстояние, образуя переднюю границу свободно движущейся грибовидной структуры. Эти два процесса приводят к тому, что асимптотически вихревая пелена, уменьшая до нуля свою интенсивность, становится стационарной поверхностью тока в системе координат, связанной с самодвижущейся структурой. Грибовидная структура превращается в вихревой тор.

Наиболее интересным является случай, когда внешний диаметр тора соизмерим с внутренним. В этом случае явно проявляется дипольный характер грибовидных структур. Математическое описание структур такого типа хорошо известно. Примером гидродинамической модели трёхмерной вихревой кольцевой структуры, эквивалентной движущемуся в жидкости диполю, является т.н. вихрь Хилла [81].(рис 3.9)

 

 

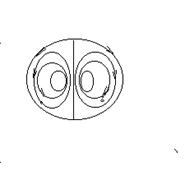
Рис. 3.9     .

Дипольная структура.

Вихрь Хилла  .

 

Задача деформации и всплывания вихревого объёма в стратифицированной жидкости решена в цикле работ И. М. Миндлина:

«Эта модель описывает эволюцию ограниченной однородной тяжёлой жидкой массы в неограниченной однородной тяжёлой жидкой среде (жидкое пятно в жидкой среде). Показано, что течение, начавшееся из состояния покоя представляет собой эволюционирующий кольцевой вихрь типа грибовидного облака, образующегося после мощного взрыва в атмосфере.» [82. С.9] . 

б) Если в процессе трансформации вихревая пелена подвергнется внешним возмущениям, то она, будучи обобщенной ударной волной, может отреагировать на возмущение формированием вторичных поверхностных волн, которые, в свою очередь, являясь существенно нелинейными, вновь формируют вихревые ударные волны первого и второго рода и вторичные грибовидные структуры. Эти вторичные вихревые и грибовидные структуры, хотя по своему происхождению являются более сложными, так как сформировавшие их поверхности после самопересечения становятся в некоторых случаях четырёхслойными, вследствие перезамыкания и последующей диссипации могут потерять память о своем происхождении и внешне выглядят как первичные грибовидные структуры или их элементы. Этот процесс является одной из форм появления древовидных структур.

В  действительности процесс "забывания"- потери информации - происходит практически на всех этапах формирования вихревых ударных волн и грибовидных структур. Это связано с тем, что потеря устойчивости в виде вихревых ударных волн первого рода происходит через спирализацию и сформировавшиеся вихревые торы должны содержать в себе память не только о двух или четырёхслойных поверхностях, но и об n-слойных поверхностях, с числом слоёв, пропорциональном числу витков спирали, породившей вихревой тор. При диссипации и многочисленных внутренних потерях устойчивости образовавшаяся  вихревая или грибовидная структура, фрактализуясь, увеличивая свою размерность на единицу, "забывает" о своём происхождении.

(Здесь уместно отметить возможную аналогию между завихрённостью и температурой.  Динамика обеих величин подчиняется уравнению типа уравнения теплопроводности. Следовательно, для завихрённости можно ввести некоторый аналог энтропии. Само формирование концентрированных вихрей - это энтропийный процесс, связанный с диссипацией энергии. Однако, этот процесс значительно отличается от процесса перехода к статическому равновесию, изучаемому в статистической физике, так как он приводит не к "тепловой смерти", а к формированию новых вихревых и грибовидных структур).

Формирование вихревых ударных волн первого рода с последующей внутренней диссипацией завихрённости представляет собой промежуточный процесс, приводящий в области формирования структуры к максимуму "энтропии завихрённости", но не к максимуму энтропии в термодинамическом смысле.

Гидродинамическим примером множественного формирования вторичных вихревых и грибовидных структур такого типа является турбулизация вихревой пелены за крылом  или турбулизация границ струйного течения.

    в) Перезамыкание вихревых поверхностей двух грибовидных структур первого топологического класса в зависимости от стороны перезамыкания может привести к появлению квадрупольных структур двух типов (рис.3.10) квадрупольной структуры, у которой пелена находится внутри торов и квадрупольной структуры, у которой пелена находится вне торов и как бы охватывает их. Во втором случае возможно сближение вихревых торов и формирование локального квадруполя.

 

 

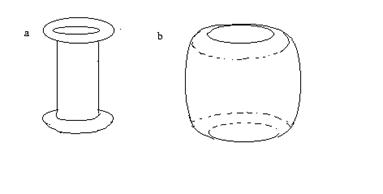
Рис. 3.10

Квадрупольные структуры .

 

Если осуществляется перезамыкание двух различных вихревых торов , то здесь также возможны два топологических варианта .

3) Вариант 1

Если перезамыкающиеся торы представляют собой элементы двух различных грибовидных структур, то слияние вихревых торов, по-видимому , автоматически приведёт к перезамыканию вихревых пелён , их соединяющих .

4) Вариант 2 

Если торы представляют две части квадрупольной структуры, то в результате перезамыкания квадрупольная структура может вновь превратиться в дипольную .

е) В некоторых случаях  теоретически возможен "захват" вихревым

тором или закрученной "ножкой"  грибовидной структуры  элементов другой грибовидной структуры , что может привести к установлению новых ближних связей и, возможно, к формированию новых структур. Этот процесс открывает возможность установления иерархии ближних связей между элементами грибовидных структур.

ё) В случае второго и третьего вариантов грибовидных  структур возможны иные качественные формы их трансформации. Одной из них является винтовая спирализация "ножки" грибовидной структуры как в случае открытого -"женского ", так и в случае замкнутого-"мужского" вариантов.

    Спирализация может совпадать с формированием концентрированных вихревых структур (так возникают кармановские дорожки за плохообтекаемыми телами и спиральные вихревые следы за шарами )

Спирализация ножки "гриба"- это фундаментальный процесс нарушения симметрии. Воронки на воде, смерчи и ураганы - возможные примеры спирализации ножки “гриба”.

Закрутка ножки грибовидной структуры может привести к появлению нового класса грибовидных структур - к структурам , названным нами клеточными .           Это может произойти в случае "разрыва"-  закрученной ножки грибовидной структуры (перезамыкания её границ) и проникновения её внутрь вихревого тора . Так может возникнуть топологический аналог биологической клетки.- грибовидная структура в виде "клетки со спирально закрученным ядром."

"Клетка со спирально закрученным ядром "- структура, динамика которой может быть исследована методами современной математической физики Например, в качестве такой модели может быть использован  полый внутренний спиральный вихрь, трансформирующийся во внешнюю дипольную оболочку (рис.20).

 

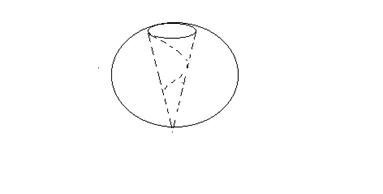
Рис.3.11.

Клеточная структура .

 

ж) Аналогия построенных вихре - волновых структур с биологическими объектами подсказывает ещё три возможные формы трансформации "мужских" и "женских" грибовидных структур -

1)           формирование на их "ножках " (по аналогии с вариантом а) новых , вторичных грибовидных структур , как на материнских поверхностях. (рис.3.12)- частичное вегетативное размножение грибовидных структур.

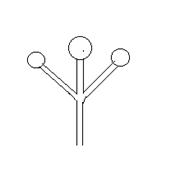
Рис. 3.12

Частичное “вегетативное” размножение грибовидных структур .

 

2) Если на вихревом торе грибовидной структуры, имевшем  первоначально форму, близкую к форме кругового тора, возникнут вследствие потери устойчивости стоячие волны, которые затем развиваясь, и увеличивая свою амплитуду, разобьют шляпку грибовидной структуры на ряд сегментов, то в случае  аналогичного процесса в ножке гриба имеем полное размножение структуры. Если же ножка гриба не расщепляется, то получается новая разновидность грибовидной структуры, названная нами с использованием биологической аналогии-"цветком" (рис.3. 13)

 

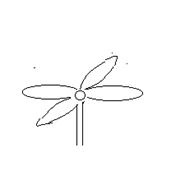
Рис.3.13

Формирование “цветка”

 

Квадрупольные структуры с пеленой, находящейся снаружи от вихревого тора, могут вследствие потери устойчивости пелены сформировать вместо одной охватывающей пелены множество внешних соединительных трубок  Примерно так устроена кровеносная система  и некоторые другие транспортно-информационные системы человека.

В большинстве  случаев описанные процессы должны иметь каскадный характер, приводящий к появлению множественности "шляпок" или "ножек"  или связанных между собой грибовидных структур. Однако, в отличие от каскада бифуркаций Фейгенбаума, вместо хаотического аттрактора, семейства грибовидных структур трансформируются в новый тип структур, которые были названы нами древовидными. Основным свойством древовидных структур является наличие связанных между собой грибовидных структур или волновых структур более низкого уровня, генетически происходящих друг от друга.

Древовидные структуры являются переходными к  принципиально новому классу вихре - волновых систем, названному нами транспортно- информационными системами..

 

5. Транспортно-информационные системы.

 

Транспортно-информационные системы состоят обычно из большого числа связанных между собой, а иногда и произошедших одна от другой грибовидных и древовидных структур или вихре - волновых структур более низких классов. В случае, если все структуры абсолютно идентичны, могут быть рассмотрены два предельных варианта .

Первый - структуры практически не взаимодействуют между собой. В этом случае они эквивалентны идеальном у газу, поведение которого описывается методами кинетической теории. Динамика большого числа таких структур почти не зависит от их внутреннего строения и при рассмотрении большого ансамбля "частиц" - грибовидных структур,- их динамика вновь описывается волновыми уравнениями. Спираль качественного анализа вихре - волновых структур совершает полный оборот, и мы вновь, на ином масштабном уровне приходим к линейным волнам .

По иному обстоит дело в случае, если между структурами существуют те или иные связи. Из нашего рассмотрения можно предположить существование между ними как минимум двух типов связей-

1) Полевых - дальних, связанных с тем , что структура сформировалась в сплошной среде, является дипольной и взаимодействует с другими структурами среды, создавая вокруг себя стационарное поле, либо посылая в среду линейные волны, умеренно нелинейные волны, вихревые или грибовидные структуры.

2) Ближних связей - определяемых генетическим происхождением грибовидных структур друг от друга. Они могут быть также связаны с перезамыканием грибовидных структур или захватом одной грибовидной структурой элементов другой  и осуществляются, например, путём транспорта массы, энергии и информации по ножке грибовидной структуры .

3) Не  исключён и несколько иной (промежуточный) тип связи, состоящий в том, что некая грибовидная структура порождает путём локального перезамыкания дочерние структуры меньшего масштаба, которые затем захватываются другой грибовидной структурой. Порождение и захват могут стать регулярными. Возможно также периодическое перемещение элементов грибовидных структур или тел - волн между двумя грибовидными структурами. Тем самым  возникают транспортные связи. То есть дочерние грибовидные структуры или более простые элементы тел - волн транспортируются либо по специальным транспортным магистралям (например, ножкам грибовидных структур) либо свободно перемещаясь в пространстве.

    Полевое взаимодействие вихревых и грибовидных структур между собой а также с порождёнными ими нелинейными волнами достаточно интенсивно исследуется в настоящее время как экспериментально, так и теоретически с использованием методов математической физики.

    В последние годы в этом направлении сделаны блестящие открытия. Так, например в шестидесятые годы  был открыт нелинейный волновой резонанс при взаимодействии поверхностных и внутренних волн на границе раздела сред различной плотности [83]. А в восьмидесятые годы  авторами с группой сотрудников было обнаружено новое явление, возникающее при движении несимметричных тел-волн в неоднородной слошной среде , названное ими вихре - волновым  и структурным резонансом.[31,84].

Вихре - волновые резонансные процессы являются одной из широко распространённых форм нелинейного взаимодействия волн и вихрей, а новые формирующиеся резонансные  структуры могут оказаться особенно устойчивыми и обладающими качественно новыми свойствами, отличными от свойств формирующих их структур. Отыскание в природе резонансных структур такого рода и их детальное исследование представляет собой перспективную научную проблему. Именно совокупность уже открытых и ещё не открытых резонансов различных  типов, по нашему мнению , является одной из основных движущих сил самоорганизации структур и систем.

Совершенно иного подхода требует исследование "ближних" связей, так как именно они в основном определяют те новые свойства, которыми обладают сложные транспортные системы. Ближние связи позволяют отдельным грибовидным структурам направленно обмениваться массой, энергией и информацией.

По-видимому, ближние связи практически всегда осуществляются "квантами" , то есть дискретными порциями, фактически такими порциями являются грибовидные структуры или их части, либо простые тела-волны. При этом такие связи оказываются четко направленными. Существование устойчивых транспортных направленных связей позволяет достаточно простыми способами осуществлять математическое описание различных систем с ближними связями. В основе этого описания лежат обычно методы теории графов и сетей , интенсивно развивающиеся в последнее время.[85]-[88]. 

Примером математического анализа динамики простейшей транспортной динамической системы является работа [89],

Несмотря на то, что четвёртый, пятый и шестой классы волновых структур и систем встречаются и в неживой природе, наиболее широко они распространены в технических, биологических и социальных системах. Поэтому общие закономерности их динамики оказываются важными не только для физики и химии, но и, главным образом, для технических приложений, наук о Земле, биологии и наук о человеке и обществе.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Посвящено 100-летию со дня рождения выдающегося учёного, профессора

Басина Абрама Мосеевича.

 

Этюд 21

Синергетический метод исследования транспортных систем.

 

Раэработанная в Синергетике классификация нелинейных волн, структур и систем включает в себя в качестве шестого типа –транспортно-информационные системы. К этому классу относятся реки и моря, атмосфера, живые организмы (в том числе и человек), биоценозы, а также транспортные системы социума.

     При этом включение транспортных систем в общую классификацию позволяет рассматривать их свойства и динамику их развития с единых позиций, применимых к любым структурам, обладающим волновыми свойствами. М. А. Басиным показано, что ТРАНСПОРТНЫЕ СИСТЕМЫ          являются одной из наиболее характерных, а, возможно, единственной формой существования грибовидных структур, представляющих собой совокупность вихревого тора (диполя) и «ножки», связывающей эту структуру либо с материнской границей, либо с другими грибовидными структурами. Совокупность связанных между собой грибовидных структур образует многополюсную транспортно-информационную систему, представляющую собой ряд дипольных центров (шляпок грибовидных структур) и транспортные артерии – ножки грибовидных структур.

Разветвлённая транспортная система, во-первых покрывает достаточно густой сетью ту часть поверхности или пространства, в которых она расположена, а во-вторых обеспечивает управляемый транспорт материи, энергии и информации к любым элементам транспортной системы. На наш взгляд, именно развитие транспортно-нформационных систем и является единственным способом, который придумала природа, а за ней и человек, для преодоления всеобщего роста энтропии, а также выработки и быстрой передачи не только материи и энергии , но и информации.

Каковы же с этих позиций основные свойства транспортных систем?

А) Открытость системы- система устроена таким образом, что в узлах системы (полюсных головках грибов ) происходит выработка и приём материи, энергии и информации.

Б) Существуют собственно транспортные элементы системы - ножки грибов- покрывающие тонкой сетью всю площадь или объём, занимаемый транспортной системой, которая осуществляет функцию  доведения материи, энергии и информации до каждого элемента транспортной системы.

В) Возможно разделение функций выработки, приёма переработки и передачи материи, энергии и информации между отдельными элементами системы, резервирование функций.

Г) Транспортные системы – системы с наименьшим ростом энтропии, системы, которые за счёт потребления энергии способны овладеть внутренней информацией, принимая внешнюю информацию., производить информацию и передавать её во внешнюю среду.

Д) Транспортные системы формируют иерархическую структуру – как сама транспортная система, так и её элементы и подсистемы представляют собой различные формы грибовидных структур.

Е) Иерархичность транспортных систем определяет квазифрактальность геометрии транспортных систем: шляпки и ножки грибов могу  формировать  грибовидные струиктуры больших масштабов

Ё) Обычно транспортные системы – саморазвивающиеся системы, стремящиеся к увеличению управляемой  массы, энергии , информации.

Ж) Создаваемые человеком транспортные системы должны строитьмся таким образом, чтобы учитывать указанные выше свойства естественных транспортных систем.

З) Необходимость выживания в условиях изменения внешней среды заставляет транспортные системы вырабатывать внутренние информационные механизмы (в настоящее время известно два таких механизма : генетический код, транспортные графы, которые являются аналогами специального информационного кода.

И) Для исследованияия нформационной и знтропийной части транспортных систем может быть использован достижения теории нрафов , деревьев

 

 

    Внутри класса информационно-транспортных систем могут быть выделены подклассы, различающиеся особенностями процессов, в которых участвуют входящие в них элементы (кванты) и подсистемы.

а) Системы квази - детерминированного типа, бифуркационные процессы внутри которых оказывают незначительное влияние на их макропараметры. Основным свойством таких систем является значительная разница между масштабами самой системы как обобщённой волны и отдельных элементов (квантов), её составляющих, а также близость геометрических параметров квантов и широкий спектр их энергетических уровней. Для их изучения существуют глубоко разработанные методы равновесной и  неравновесной статистической физики, термодинамики и механики сплошных сред. При этом квази-детерминированность на системном (обобщённо - волновом) уровне допускает различную степень хаотичности на уровне квантов. Большинство макроскопических объектов неживой природы относится к этому подклассу.

б) Транспортно - информационные системы, у которых реализуется иерархическая материальная и информационная связь между уровнем системы - волны и элемента – кванта. В таких системах обычно выстраивается масштабная иерархия подсистем, каждая из которых может обладать свойствами волновых структур классов более низкого уровня. Эта масштабная иерархия имеет обычно квази - фрактальный характер. При этом общее число квантов, входящих в систему, оказывается значительно больше, чем число уровней иерархии. Именно в таких системах экспериментально наблюдается соответствующее их квази - фрактальной структуре степенное статистическое распределение масштабов элементов и подструктур. Отмечая главное свойство таких систем, наличие связей между уровнями иерархии, которое называют целостностью, Ю.К. Крылов назвал такие системы интаэросистемами, и предложил назвать науку, их изучающую, интаэрологией [90-92]. Интаэрология Ю. К. Крылова может стать одной из базовых составляющих синергетической методологии.

      В транспортно - информационных системах в ряде случаев может существовать некоторая величина, например, энергия, расход или объём, передаваемая с одного уровня иерархии на другой без изменения, что также обеспечивает целостность системы. Это условие является основанием для названия данного нами такого рода системам - «идеальный трансформер» [93].

 Транспортно- информационные системы, второго и более высоких подклассов могут быть способными к размножению, то есть к формированию себе подобных систем. Способность к размножению не является прерогативой только транспортно- информационных систем. Практически в той или иной степени это свойство характерно для любых колебательных и волновых систем, начиная от линейных колебаний и волн. Однако, когда мы переходим к рассмотрению транспортно – информационных систем второго и более высоких подклассов, то их размножение может иметь специфический характер, проявляя, особенно у живых систем, такую сложность, которую невозможно даже помыслить у структур более простых типов. Здесь возникают структурно-волновые резонансы и могут появляться логарифмические законы распределения параметров элементов. В последние годы большое внимание уделяется исследованию в таких системах специфических форм резонанснсных явлений, называемых гармоническими резонансами, родственными цепочкам кратных резонансов в нелинейных колебательных системах. Формирование резонансов такого типа осуществляется как каскадный процесс, передающий энергию и информацию с одного уровня иерархии на другой. Анализ процессов такого типа приводит в простейшем случае к геометрической прогрессии временных и пространственных масштабов, а на следующих уровнях рассмотрения – к обобщённым рядам Фиббоначи и теории ритмокаскадов.[1,49,93-102] 

в. Транспортно- информациионные системы, способные моделировать  свою динамику и динамику окружающей среды – поля и выбирать близкие к оптимальным модели бифуркационного поведения. Именно у таких систем интенсивно развивается, определяя их эволюцию, внутренний контроллер, который назван нами гомеостатическим [41- 46].

г. Транспортно- информационные системы, обладающие сознанием и творческими способностями. 

Так как транспортно – информационные системы обычно состоят из большого числа элементов, которые могут отличаться как масштабами, так и другими параметрами, то при исследовании этих систем существенную роль играют соответствующие статистические закономерности.

Эти закономерности должны быть различными для  транспортно-информационных систем двух первых подклассов. Ввиду сложности иерархической структуры систем второго и более высоких подклассов в них могут встречаться и распределения параметров, свойственные для систем других более низких подклассов. Этой проблеме в настоящее время посвящено значительное количество работ, обзор которых дан в ряде статей и  монографий (см., например, [90-93]). При этом, в большинстве работ было показано, что если система находится в состоянии статистического равновесия, то при возрастании количества элементов системы, распределения  элементов по их свойствам оказываются со всё более возрастающей точностью удовлетворяющими нескольким достаточно простым законам. Для систем первого типа это закон, описываемый показательными функциями, приводящий к основным соотношениям равновесной термодинамики, а для систем второго типа – это гиперболическая или более общая степенная зависимость, имеющая очень много названий, так как она была обнаружена в различных областях знаний.

Мы будем в дальнейшем придерживаться терминологии [90-92] и называть это распределение распределением Ципфа - Мандельброта. Существование подобной зависимости и её универсальность свидетельствовали о том, что системы второго класса, куда относятся и многие самоорганизующиеся системы, обладают некоторым своим универсальным свойством, аналогичным второму закону термодинамики, которое заставляет эти системы стремиться к некоторому состоянию, статистические свойства которого отличаются от термодинамически - равновесных. Возникал также вопрос о связи закона Ципфа - Мандельброта с экспоненциальными распределениями, характерными для систем первого подкласса. Для решения этих проблем предлагались различные физические модели.

    Авторы, например, обратили внимание на формальную аналогию между гиперболическим статистическим распределением и параметрами потока от вихрей и источников, в которых сохраняется расход и циркуляция, что позволило искать аналогии в поведении таких систем с вихревыми и грибовидными (дипольными) структурами. Кроме того, гиперболический закон изменения амплитуды колебаний и волн в зависимости от частоты наблюдается при резонансных явлениях, что в некоторых случаях, возможно, свидетельствует о резонансной природе возникновения распределения Ципфа-Мандельброта.

    Важной проблемой является исследование нестационарных режимов, приводящих асимптотически к гиперболическим и более общим степенным распределениям. Прорывом в этом направлении оказалась теория самоорганизованной критичности, которая вскрыла один из возможных механизмов выхода системы второго класса на статистически равновесное для неё состояние со степенным законом распределения [74 ].

    Большой вклад в исследования нетрадиционных, как их ранее называли, распределений внесли Ю. К. Крылов и Б. И. Кудрин, исследовавшие  многие математические особенности этих распределений и получившие богатый эмпирический материал [90 - 92].

    Однако распределения Ципфа-Мандельброта имеют настолько всеобщий характер и возникают в различных, системах и процессах: природные катастрофы, лесные пожары и землетрясения, рыночная экономика и распределение числа слов в словаре и тексте, количество книг и учёных, распределение видов в популяции и т.д. и т.п., - что можно предположить, что должен существовать некий универсальный закон природы, выражаемый самыми общими математическими формулами, не зависящими от той интерпретации, которая будет ему дана.  Попытка отыскания такого закона была сделана Б.И. Кудриным и Ю.К. Крыловым, показавшими, что  степенному закону удовлетворяют распределения простых множителей набора целых чисел, что ещё раз указало на универсальность этого закона распределения, но не полностью решило проблему [92]. Ещё один, более близкий к динамике систем подход, являющийся обобщением подходов Гиббса и Больцмана,  был  предложен  Ю.К. Крыловым [90]. По его мнению, получение того или иного закона может быть осуществлено на пути, начатом Больцманом при выводе экспоненциального закона распределения частот встречи состояний молекул в зависимости энергии этих молекул. А именно, отыскание такого распределения, которое даёт максимум числа разбиений множества на классы при некоторых дополнительных ограничениях [90]. Путь, намеченный Ю. К. Крыловым оказался наиболее плодотворным. На этом пути В. П. Маслову [103] удалось доказать общую математическую теорему о свойствах множества отображений элементов множества целых чисел , обладающих тем свойством, что их сумма постоянна и равна заданному числу  на совокупность  упорядоченных неотрицательных чисел  при некотором дополнительном условии  относительно заданного числа . Результатом этой теоремы явилась возможно/сть обоснования распределения Ципфа-Мандельброта и более общих законов распределения особенностей в динамических системах.

Анализ динамики грибовидных структур и тел–волн позволил предсказать  возможность появления принципиально нового типа взаимодействий, сущность которого состоит в аномальном взаимодействи умеренно нелинейной  волны – границы, - как с внутренним объёмом, так и с внешней средой. Качественный анализ такого нелинейного взаимодействия позволил обосновать механизм возникновения нового  явления – вихре - волнового и структурного резонанса. Основными необходимыми условиями возникновения открытого явления являются пространственная близость в течение определённого промежутка времени взаимодействующих тел и (или) волновых картин, равенство их масштабов и способность их к взаимодействию с полем, приводящая к изменению некоторых основных свободных параметров взаимодействующих объектов.

    Вихре - волновой и структурный резонанс может явиться одним из главных механизмов возникновения и стабилизации структур от нана- масштабов до масштабов Вселенной.- то есть одной из причин структуро- и системо - формирования, в частности, у биологических объектов и в социальных системах.

    Характерным примером цепочки таких структурно-волновых  резонансов является игра на инструменте виртуоза-скрипача. Жёстко закреплённая струна представляет собой в первом приближении одномерную среду с упругими свойствами, определяющими тип волнового уравнения  и соответствующее дисперсионное соотношение. Закрепление струны  вводит в действие структурно - волновое её взаимодействие с корпусом инструмента, представляющим тело-волну. Это взаимодействие является резонансным, так как определяет однозначно спектр длин допустимых стоячих волн, которые могут выжить в струне. А дисперсионное соотношение, определяемое упругими свойствами струны, в свою очередь однозначно определяет спектр частот колебания струны. Это первый структурно – волновой резонанс, который достаточно просто описывается математическими формулами и порождает то, что мы обычно называем собственными колебаниями струны. Вторая стадия резонансного взаимодействия состоит в непосредственном соприкосновении двух тел-волн – закреплённой струны и смычка. Движение смычка относительно струны приводит к локальному перемещению и количественному изменению сил, действующих на струну, и связанных с ними её перемещений. Тем самым на волновую систему, представляющую собой закреплённую струну воздействует другая волновая система (тело-волна)- смычок. Это воздействие связано с изменением правой части уравнения, описывающего силовое механическое взаимодействие. Воздействие смычка может быть представлено в виде интеграла Фурье, из всего спектра которого за счёт резонанса выживают только те гармоники, которые совпадают с собственными гармониками системы струна - инструмент. Здесь второй раз действует структурно- волновой резонанс.

Колеблющаяся струна находится в поле - воздушной сплошной среде. Характеристики этой сплошной среды также описываются собственным волновым дифференциальным уравнением. Свойство воздушных звуковых волн таково, что их скорость постоянна. Спектр допустимых звуковых волн практически непрерывен. Волновое взаимодействие колеблющейся струны с воздушной средой также является резонансным. Из всех возможных звуковых волн резонансно  возбуждаются лишь те, которые имеют частоты, соответствующие частотам колебаний струны. Еще один резонанс не только закрепляет резонансные частоты, но и передаёт их в другую среду, обладающую новыми свойствами - свойствами передачи резонансной частоты на большие расстояния с большой скоростью – скоростью звука. Далее может быть включён ещё один резонатор, зрительный зал, представляющий ещё одно тело-волну, который резонансно усиливает звуковые волны, заставляя их отражаться от границ, размеры которых подобраны таким образом, чтобы возникал пространственный волновой резонанс с размерами звуковых волн. Далее в действие вступает новый структурно-волновой резонанс, между улиткой уха и звуковыми волнами. Улитка представляет собой сложную спиральную струну, собственная частота колебаний которой на различных участках спирали различна. Поэтому, с каждой звуковой волной резонансно взаимодействует только один участок улитки. Механические колебания улитки уха резонируют в электрическими импульсами колебаний нейронов, которые передаются в мозг. Резонансное узнавание мелодии позволяет замкнуть процесс исполнения музыкального произведения через человека – музыканта, который управляет движением смычка таким образом, чтобы вся цепочка резонансов замкнулась в виде приятной и знакомой мелодии.

    Такой же качественный волновой анализ цепочки резонансов может быть проведён и для зрительного, и для обонятельного, и для вкусового, и для тактильного восприятия. 

    Взаимодействие тел-волн а также грибовидных структур с окружающей средой, основные закономерности которого описываются в настоящее время наиболее полным образом методами динамики сплошной среды, обладают некоторыми специфическим свойствами, которые мы попытаемся описать словесно. Движение тела - волны в сплошной среде (например, жидкости или газе) вызывает в среде формирование поля локальных распределений давления, которое в случае равномерного перемещения тела движется в виде стационарной присоединённой картины (в чём также можно увидеть резонансный процесс, ведь скорость перемещения тела и скорость перемещения картины давлений, им вызванной, имеют одинаковую величину). Тело как бы извлекает из всех возможных полей давлений то, которое имеет ту же скорость перемещения, что и само движущееся тело. Это одна из форм структурно-волнового резонанса - резонанса по скорости. Однако, реальная структура потока оказывается значительно более сложной. Наряду с волной давления тело формирует движущуюся с той же скоростью волну, описывающую поле вызванных скоростей. При этом в частном случае несжимаемой невязкой среды эти поля оказываются жёстко связанными – поле давлении однозначно определяется полем скоростей и наоборот. В других, более общих случаях, картины поля скоростей и поля давлений связаны лишь частично. Если в сплошной среде имеются неоднородности или среда сжимаема, то влияние этих аномалий приводит к необходимости рассмотрения дополнительных дифференциальных уравнений в частных производных, в решениях которых присутствуют только те волновые частоты, которые удовлетворяют этим уравнениям. Тем самым резонанс между неоднородностями среды, которые можно в свою очередь считать частным случаем умеренно-нелинейных волн, и самой сплошной средой отбирает из всего спектра возможных волн те, которые удовлетворяют заданным ограничениям. Дополнительное резонансное взаимодействие этих оставшихся волновых структур с движущимися телами существенно меняет структуру волн давлений и скоростей, присоединённых к движущемуся телу.

   

 

 

                                                                            

                                             

                                                           Этюд 22

 

 Вихре- волновой и (или) структурный резонанс. История открытия.

 

1.                                                                                                                                                                                                              Нелинейные резонансы поверхностных и внутренних волн в стратифицированной жидкости.

 

Исследованию волновых движений в сплошной среде посвящена обширная литература, в том числе и большое количество монографий (см., например,[10], [51], [105], [151-153], [156]). И хотя первичный анализ линейных моделей волновых течений в неоднородных средах не указывал прямо на наличие какого-либо резонансного взаимодействия возникающих волн между собой, однако, в последние десятилетия рядом учёных было открыто и широко исследовано резонансное взаимодействие нелинейных поверхностных и внутренних гравитационных волновых движений. О. M. Филлипсом, М. Лонге-Хиггинсом, Д. Бенни, В. Е. Захаровым, А. Б. Шабатом, Л. М. Бреховских и его группой, Дж. Уиземом и другими исследователями был теоретически предсказан, а затем экспериментально подтвержден и подробно изучен нелинейный волновой резонанс между поверхностными и (или) внутренними волнами [105]. Им удалось обнаружить теоретически и исследовать экспериментально условия возникновения волнового резонанса. Такими условиями, справедливыми как для поверхностных, так и для внутренних волн, явились следующие [105].

  

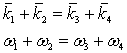
Здесь - волновые векторы и частоты двух взаимодействующих волновых движений; - волновые векторы и частоты резонансных волн.

Более 30 лет тому назад одним из авторов была высказана гипотеза о том, что аналогичные резонансные явления должны возникать и при взаимодействии движущихся тел с диспергирующими волнами, возникающими в сплошной среде.

 

2.                                                                                                                                                                                                              Результаты теоретических и экспериментальных исследований сил, действующих на тела, движущиеся в ограниченном водоёме или обтекаемые ограниченным потоком. Критические значения чисел Фруда по длине тела и глубине жидкости.

 

При равномерном поступательном движении надводного судна или произвольного тела вблизи свободной поверхности воды с постоянной скоростью ему сопутствует сложная волновая картина, которая в системе координат, связанной с телом, остаётся неизменной.

 Вот как описывается эта картина в [111].

 « При равномерном и прямолинейном движении судна форма свободной поверхности представляет собой волновой рельеф, который движется одновременно с судном с той же скоростью, что и у судна, и не изменяет своей конфигурации. Поскольку основными волнообразующими центрами являются участки корпуса со значительной кривизной поверхности, возникают две системы волн – носовая и кормовая. В носовой и кормовой системах различают расходящиеся и поперечные волны. Расходящиеся волны состоят из рядов сравнительно коротких, слегка вогнутых гребней, располагающихся симметрично относительно ДП (диаметральной плоскости) судна. Фронт каждой волны образует с ДП угол , величина которого на глубокой воде не изменяется при изменении скорости судна. В зависимости от остроты носовой ветви ватерлинии судна угол  составляет 36-40 град. Если соединить центры гребней расходящихся волн, то можно получить прямую, составляющую с ДП угол, равный 0.5.»

Результаты многочисленных теоретических и экспериментальных исследований волн, образующихся при движении судна на глубокой воде при значениях чисел Фруда по длине судна , (где  - длина судна в метрах), близких к 0.5, позволили обнаружить специфическую картину взаимодействия судовых поперечных волн, когда носовая волна усиливает кормовую и растет волновое сопротивление судна. При этом половина длины поперечной волны, создаваемой движущимся судном, оказывается равной длине судна. Однако это явление не рассматривалось ранее как резонансное, в основном, вследствие отличия от общепринятого  представления о резонансном взаимодействии колебательной системы с внешним периодическим воздействием. Его теоретическое исследование выполнялось с помощью линейной теории, результаты которой не указывают прямо на резонансный характер взаимодействия. В данном случае ранее говорилось лишь о благоприятной или неблагоприятной интерференции линейных волн, так как никакого дополнительного усиления интенсивности источников, заменяющих судно, в линейной модели, которая качественно описывала волновую картину и позволяла приближённо рассчитывать волновое сопротивление, не учитывалось.

С уменьшением глубины водоёма значения , при которых наблюдается горб волнового сопротивления, уменьшаются и стремятся к нулю при предельном мелководье, когда становится малой величиной (здесь - глубина водоёма). В предельном случае очень малых относительных заглублений волновая картина определяется другим параметром - числом Фруда по глубине погружения . В пределе при , стремящемся к нулю, наблюдается одна поперечная волна, отходящая от носа судна, амплитуда которой становится максимальной при . При относительных скоростях, больших , поперечные волны исчезают, а волновое сопротивление резко уменьшается.  Аналогичные явления наблюдаются и при обтекании препятствия. Вот что пишет Джеймс Лайтхилл, описывая обтекание  препятствия потоком весомой жидкости [34. С. 319]:

«Мы опишем очевидно парадоксальный случай волн, которые образуют совершенно стационарное течение. Во всех точках потока, (включая и те, в которых находятся волны) течение является стационарным: скорость жидкости не меняется со временем. Хотя подъём поверхности и может локально обнаруживать правильное, почти синусоидальное изменение в пространстве, он не обнаруживает никакого изменения во времени: гребни волн всегда остаются на тех же местах при движении потока. Стационарная картина волн порождается совершенно неподвижным препятствием в потоке. Это препятствие может быть просто местной особенностью дна. В своём стихотворении «Ручей, текущий к западу»[210]  Роберт Фрост писал:

«Чернеющие воды, налетая

На затонувший камень, разбивались

И вспять бежали белою волной

Так белая на чёрных мчалась вечно,

Не наступая и не отступая…»

Постоянство потока поразило его воображение

«Волна та отражается от камня

С тех пор, как реки по земле текут»

Он увидел, что распространение гребня вверх по потоку может в точности сводиться на нет течением вниз по потоку.

«Мы все перечим. Белою волной

Ручей течёт наперекор себе»     

Он образно объяснил происхождение явления:

«Вот это устремленье вспять, к истоку,

Наперекор теченью, что несёт нас,

Есть дань теченья своему истоку.»»

Классические методы изучения взаимодействия тел, движущихся в весомой жидкости, с волновыми системами, создаваемыми на свободной поверхности, основанные на линейной теории волн, были разработаны еще в конце Х1Х века и интенсивно развивались вплоть до последнего времени, в частности, применительно к исследованию судовых волн [106]- [111].

 

 

3. Движение крыла вблизи границы раздела сред. Аномальные режимы обтекания. Результаты теоретических исследований.

.

При движении вблизи свободной поверхности или глиссировании несимметрично обтекаемого несущего тела, что характерно для быстроходных судов, картина существенно меняется. Постановка и общее решение такой задачи были выполнены в ряде классических работ, в частности, в работах Н. Е. Кочина [108], М. В. Келдыша и М. А. Лаврентьева [112] и Л. И. Седова [113]. Получение однозначного решения таких задач без дополнительных допущений оказывается невозможным. При их постановке, как уже отмечалось нами ранее, вводится дополнительное нелинейное условие на поверхности крыла или глиссирующей поверхности - конечность скорости в районе острой задней кромки (условие Жуковского – Чаплыгина - Кутта). Выполнение этого граничного условия, сохраняя при линеаризации граничных условий на крыле и свободной границе линейную зависимость характеристик потока от угла атаки, приводит к нелинейной обратной связи между циркуляцией на поверхности крыла и параметрами волновой системы, образующейся при его движении вблизи свободной поверхности жидкости.

Численные расчеты гидродинамических характеристик подводных крыльев выполнялись различными авторами первоначально лишь для сравнительно больших глубин погружений крыла и предельных случаев больших или очень малых значений числа Фруда по хорде крыла  [114-120]. Это было связано с практическими потребностями - суда на подводных крыльях имеют основной режим движения, соответствующий большим значениям числа Фруда.  Попытки выполнения расчетов при малых погружениях и произвольных значениях чисел Фруда приводили к значительным математическим трудностям, связанным с необходимостью вычисления сложных волновых интегралов и решением сингулярных интегральных уравнений теории крыла. Часть этих трудностей была преодолена в конце пятидесятых, в начале шестидесятых годов, когда А.Б. Лукашевичем [121], А. Н. Панченковым [122], Т.Нишиямой [123] , В. Исаи [124] и др. в дополнение к данным М.В. Келдыша и М.А. Лаврентьева были выполнены отдельные расчеты гидродинамических характеристик крыла, движущегося вблизи поверхности весомой жидкости. Обобщение этих результатов было представлено в монографиях [121, 125].

Однако, выполнить расчеты гидродинамических характеристик подводного крыла во всем диапазоне чисел Фруда и относительных глубин погружения не удавалось долгое время ни одному из специалистов. Лишь  в конце 70-х, начале 80-х годов подобные расчеты  были выполнены в США [126] при отработке численных методов решения нелинейных волновых задач. Был обнаружен диапазон параметров потока, при котором нелинейные численные методы не дают сходящегося решения. Экспериментальные данные о  волнах при буксировке подводного крыла были получены Дж.Дунканом [140]

    В 1982 году на организованной М. А. Басиным и Ю. И. Фаддеевым  конференции: “Гидродинамика подводного крыла и глиссирующих поверхностей” М. А. Басиным [127], А. Я. Ткачом [128], М. А. Макасеевым [129], М. В. Лотфуллиным [130], А. Н. Лордкипанидзе [131] были сделаны доклады по результатам новых теоретических и экспериментальных исследований гидродинамических характеристик крыла, движущегося вблизи свободной поверхности весомой жидкости. (Эти исследования были заказаны организаторами конференции). Результаты выполненных расчётов показали существование диапазона значений чисел Фруда и относительных глубин погружения крыла, при котором наблюдается аномальное поведение гидродинамических характеристик крыла. В дальнейшем М. А. Басин, А. Н. Лордкипанидзе и А.Я. Ткач [132-134], [169-174], усовершенствовав расчетные схемы с использованием квадратурных формул Корнейчук –Мишкевича -Гур-Mильнера [135-137], провели в рамках линейной теории систематические расчетные исследования по изучению влияния числа Фруда, относительного заглубления, угла атаки, формы и толщины профиля, а также удлинения крыла на его суммарные и распределенные гидродинамические характеристики при движении вблизи свободной поверхности воды. Позднее аналогичные расчеты по линейной и нелинейной теории,  были выполнены М. В. Лотфуллиным C. И. Филипповым [138] B. Г. Щигуновым [139]. и другими исследователями.

 

 

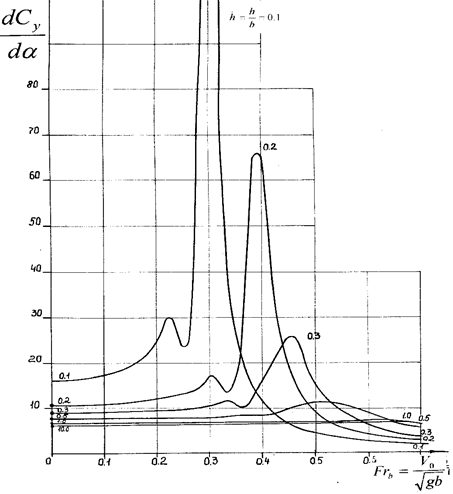
  Описание: PICT501

Рис 4.1. Расчетные графики зависимости производной от коэффициента подъемной силы по углу атаки в функции от числа Фруда по хорде крыла для тонкого профиля, движущегося под свободной поверхностью весомой жидкости при различных относительных заглублениях(результаты расчетов по линейной теории ).

   

На рис. 4.1 представлены результаты расчётов по линейной теории зависимости производной от коэффициента подъемной силы по углу атаки в функции от числа Фруда по хорде крыла  для тонкого профиля, движущегося под свободной поверхностью весомой жидкости при различных относительных заглублениях.

Как показали результаты расчетов, при приближении крыла к свободной поверхности воды, начиная с , при определенном для каждого из относительных заглублений числе Фруда по хорде крыла, уменьшающемся при уменьшении глубины погружения, наблюдается интенсивный рост производной (где - коэффициент подъемной силы крыла, - подъемная сила крыла, - плотность жидкости, - площадь крыла в плане).

Так, например, при относительном заглублении =0.2 и значении числа Фруда по хорде  линейная теория предсказывает более чем десятикратный рост по сравнению со случаем бе зграничной жидкости. С уменьшением относительного заглубления теоретическое значение максимума кривой зависимости от  резко увеличивается и даже стремится к бесконечности при . Теория предсказывает существование режима с обострением [48].

Представляет интерес зависимость от комбинированного числа Фруда, сформированного по площади жидкости над крылом  

 

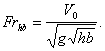
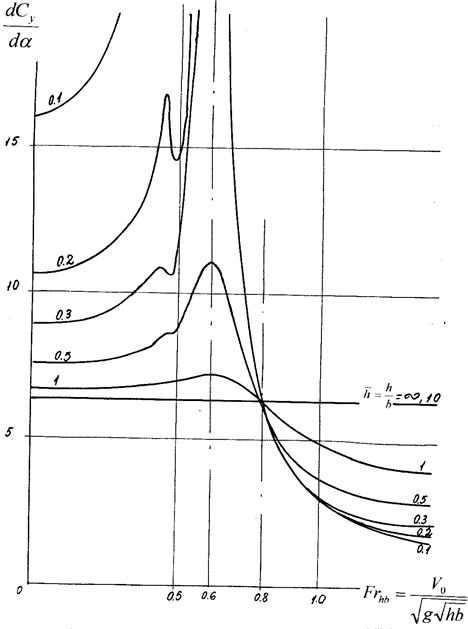
Описание: PICT502

 

Рис.4.2. Расчетные графики зависимости производной от коэффициента подъёмной силы по углу атаки в функции от числа Фруда по хорде и заглублению крыла 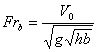для тонкого профиля, движущегося под свободной поверхностью весомой жидкости при различных относительных заглублениях (результаты расчетов по линейной теории )

Положение пика  в широком диапазоне значений , практически не изменяется и соответствует величине . При значении  заглубление практически не влияет на подъёмную с илу плоской пластинки (все кривые зависимости в функции от  пересекаются практически в одной точке при значении)

Уменьшение удлинения крыла приводит к уменьшению величин резонансных пиков, однако, значения чисел Фруда, соответствующих наступлению аномального роста значения  при этом практически не изменяются.

С уменьшением относительной глубины погружения значение числа Фруда по хорде, соответствующее аномальному режиму, уменьшается и стремится к нулю при очень малых заглублениях, тогда как число Фруда по глубине погружения-  растёт и стремится к 1. Аналогичные аномальные изменения силового воздействия на  искривленные крылья (при несколько больших значениях чисел Фруда) были обнаружены в результате расчетов зависимости угла нулевой подъемной силы, определяемой кривизной профиля, от числа Фруда и относительной глубины погружения (рис.4.3). Если в диапазоне чисел Фруда  от единицы до бесконечности для тонкого профиля в виде дуги круга угол нулевой подъемной силы практически не меняется и имеет отрицательную величину, приближенно равную в радианах , где - максимальная относительная стрелка погиби дужки, то в диапазоне чисел Фруда от 0.4 до 0.8 наблюдается резкий рост угла нулевой подъемной силы, который при  становится положительным.

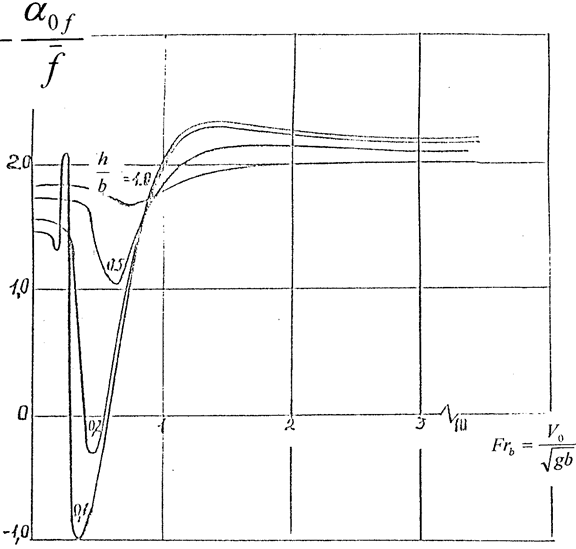
Описание: PICT503

Рис. 4.3. Расчетные графики зависимости отношения угла нулевой подъемной силы (в радианах) тонкой параболической дужки, движущейся под свободной поверхностью весомой жидкости к её максимальной стрелке погиби в функции от числа Фруда по хорде при различных относительных заглублениях  (результаты расчетов по линейной теории).

 

Линейная теория, таким образом, предсказывала парадоксальный результат. У тонкого профиля, имеющего форму выпуклой по направлению к свободной поверхности дуж  ки, при  и  должна возникать не подъёмная, как обычно, а значительная топящая сила.

Еще более необычный аномальный эффект предсказали результаты расчётов по линейной теории у крыльев с телесным профилем, имеющим  относительную толщину .

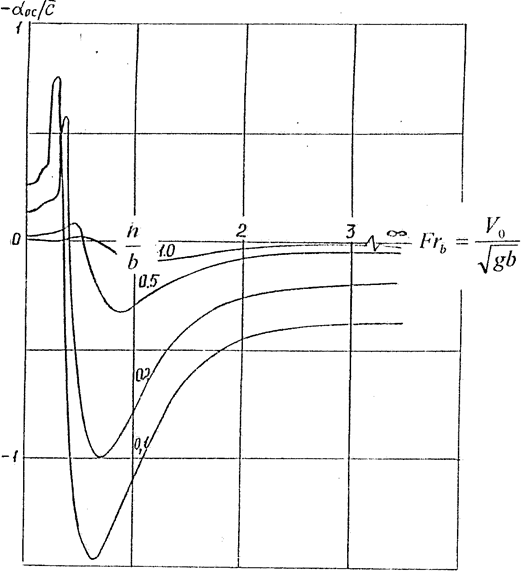
Описание: PICT504

Рис. 4.4.Расчетные графики зависимости отношения угла нулевой подъемной силы (в радианах) тонкого симметричного профиля, движущегося под свободной поверхностью весомой жидкости, к его максимальной относительной толщине в функции от числа Фруда по хорде при различных относительных заглублениях  (результаты расчетов по линейной теории ).

 

У симметричных профилей крыльев при попадании в аномальный режим также обнаружено теоретически резкое изменение угла нулевой подъемной силы, который при незначительном увеличении числа Фруда совершает зигзагообразный скачок от большого отрицательного значения до еще большего (примерно в 2 раза) положительного значения.

 Эти теоретические результаты, во-первых, должны были получить соответствующее физическое объяснение, а, во вторых, требовали экспериментальной проверки. Хотя имевшиеся разрозненные экспериментальные данные [126], [127], [131], [140] качественно подтверждали существование аномальных эффектов, однако, до выполнения систематических расчетов подробный анализ этого режима не проводился.

С целью отыскания теоретического объяснения полученных результатов были выполнены расчеты распределения давлений по поверхности крыла в этом режиме и созданы дополнительные подпрограммы расчета деформации свободной поверхности воды вблизи крыла. Результаты последних приведены на рис.4.5.

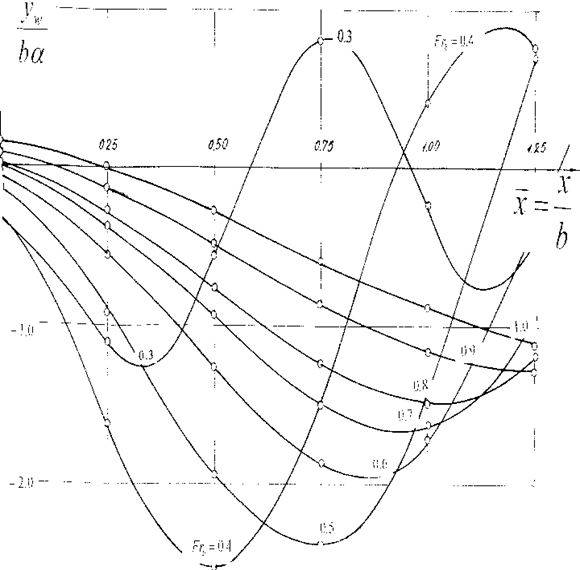
Описание: PICT505a

 

Рис.4.5. Результаты расчетов относительной деформации свободной поверхности весомой жидкости над тонкой плоской пластиной, обтекаемой под углом атаки  в зависимости от числа Фруда по хорде крыла  при относительном заглублении = 0.2 (результаты расчетов по линейной теории ).

 

Эти расчеты показали, что главным критерием, определяющим условие максимального теоретического значения величины , является совпадение определенной части длины сопутствующей волны, формирующейся на свободной поверхности, с хордой крыла. При этом для максимального воздействия на различные составляющие подъёмной силы эта часть длины волны может оказаться различной, что несколько сдвигает по числам Фруда пики воздействия на  и на угол нулевой подъемной силы .

Аномальные явления, приводящие к усилению степени гидродинамического взаимодействия несущих тел и окружающей среды, однако, значительно менее интенсивные, предсказаны теоретически и наблюдались в процессе эксперимента при движении крыла вблизи твёрдого экрана. В этом случае, соответствующем на рис 4.1 стремлению к нулю числа Фруда по хорде крыла, также был обнаружен теоретически и экспериментально подтверждён эффект, связанный со значительным ростом подъёмной силы крыла и уменьшением сопротивления при приближении к экрану. Рост аэродинамического качества в этом режиме движения был использован при создании быстроходных судов и аппаратов. [121]

 

4.Кавитационное обтекание крыла. Аномалии переходного режима. 

 

         Ещё одним явлением, при изучении которого было обнаружено аномальное поведение потока около крыла, явился переходный режим кавитационного обтекания подводных несущих поверхностей, выступающих частей и лопастей гребных винтов быстроходных судов.

 Развитие кавитационных явлений на поверхности крыла начинается при критическом числе кавитации потока. которое приближённо определяется как величина, близкая к максимальному коэффициенту разрежения на поверхности крыла или в некоторой области течения вблизи крыла (вихревая кавитация) [121].

Можно условно выделить три основных режима  кавитации профиля крыла при углах атаки, близких к расчётным:

Режим частичной кавитации, когда кавитационные явления наблюдаются в зоне длиной, не превышающей 0.6 - 0.7 хорды крыла (плавный характер обтекания задней кромки в этом режиме практически не нарушается);

Переходный режим, когда район замыкания хвостовой части каверны находится в непосредственной близости от задней кромки крыла. Нестационарный автоколебательный характер течения проявляется при этом наиболее сильно и приводит к резкому, близкому к периодическому изменению сил со временем.

Режим развитой кавитации, когда хвостовая часть каверны находится на значительном (более полухорды) расстоянии от задней кромки крыла и нестационарность в районе её замыкания сказывается на силах в значительно  меньшей степени, чем при втором режиме.

Характер развития кавитации в каждом из указанных режимов зависит от формы профиля крыла, его удлинения и, в значительной мере, от угла атаки крыла.

Частичная кавитация наблюдается в двух формах: пузырьковой и плёночной, или присоединённой. Первая форма кавитации развивается при малых, так называемых безударных углах атаки, значения которых (в радианах) не превосходят относительной толщины профиля. В этом диапазоне углов атаки эпюра разрежений на засасывающей поверхности подводного крыла близка к равномерной.

Область кавитации представляет собой не сплошную полость, а скопление интенсивно растущих, а затем схлопывающихся пузырей, заполненных парами воды или смесью паров воды и воздуха. Расширение и схлопывание пузырей происходит в пределах хорды крыла. Согласно гипотезе А.Н. Иванова  влияние этой формы кавитации на осреднённые во времени гидродинамические характеристики крыла эквивалентно влиянию стационарной зоны постоянного давления, равного давлению насыщенных паров воды  при данной температуре. Использование этой гипотезы позволяет при теоретическом исследовании заменить зону пузырьковой кавитации эквивалентной присоединённой каверной [121 ,199].

При увеличении угла атаки крыла наступает момент, когда коэффициент разрежения в районе носовой кромки профиля превышает его значение в районе максимальной относительной толщины. Вследствие изменения распределения давлений вблизи носовой кромки профиля возникает единая присоединённая каверна, в хвостовой части которой течение нестационарное. Аналогично развивается частичная кавитация при отрицательных углах атаки, когда в районе носовой кромки профиля на нагнетающей поверхности крыла возникает пик разрежения.

Экспериментальные исследования показали, что, пока длина присоединённой каверны не превысит 0.6 - 0.7 хорды, изменения подъёмной силы вследствие нестационарного характера течения в её хвостовой части малы по сравнению со средней величиной подъёмной силы, действующей на крыло, и ими можно пренебречь. Это позволяет при теоретическом решении задачи о крыле с частичной присоединённой каверной считать течение стационарным и исследовать его с помощью методов установившихся струйных течений идеальной жидкости. В некоторых случаях на засасывающей поверхности крыла развивается  система присоединённых каверн малого удлинения, начинающихся в районе носовой кромки крыла. Участки поверхности крыла между этими кавернами свободны от кавитации. Следует отметить, что характер развития частичной кавитации и её формы (пузырьковая, присоединённая или система присоединённых каверн малого удлинения ) в основном определяются формой носовой кромки профиля и углом атаки крыла и связанными с ними эпюрами распределения давлений. Иногда на крыле одновременно наблюдаются различные формы частичной кавитации. Например, при малых отрицательных углах атаки крыла сегментного профиля   на его нижней стороне развивается присоединённая форма кавитации, а на верхней, в районе максимальной относительной толщины профиля, - пузырьковая.

    При углах атаки крыла, превышающих критические, наблюдается вихревая кавитация внутри зоны оторвавшегося пограничного слоя, возникающая не на самой поверхности крыла, а на некотором расстоянии от него.

    Исследования кавитационных течений при движении тел в жидкости, выполненные рядом авторов [121, 175-178, 185-201], позволили теоретически решить в рамках стационарной теории струй невязкой жидкости большое количество проблем, связанных с этим разделом гидродинамики.  В работах А.Н. Иванова [185, 186, 199], М. П. Тулина [187-188], Дж. Гюрста [189], Р. Вейда [190], А. Г. Терентьева [191], М. А. Басина [111, 121, 175-178,193], И.Т. Егорова [175], М.А. Баевой и Л.П. Зилиста [121,178], A. В. Шалларя [121,176,177, 192, 193], Б.В. Косова [192] И.Г, Шапошникова [121 178] и других исследователей показано теоретически, что при кавитационном обтекании крыла в режиме, когда длина каверны оказывается близкой к хорде как результаты нелинейной теории струй идеальной жидкости, так и квазилинейной теории указывают на существование аномальных параметров каверны и сил, действующих на крыло.

    Экспериментальные исследования колебаний каверны, выполнявшиеся Кнэппом [194], а также В.П. Ильиным и Ю. Л. Левковским [195, 196] и другими исследователями показали, что при приближении длины каверны к длине хорды крыла амплитуда этих колебаний интенсивно растет и частота их уменьшается. Силовые измерения в этом режиме кавитации проводились различными авторами : О. Вальхнером[197], Нумахи [198], А.Н. Ивановым [199], М.Мейером [200] а также И. Т. Егоровым, М. А. Басиным, Ю.М. Садовниковым, А. В. Шалларем, Б. В. Косовым , Е.Б. Ануфриевым , И.Г.Шапошниковым и другими авторами [176-178, 192-193.207-209, 121].

    Было показано, что в этом режиме, во-первых, происходит резкое увеличение сил, действующих на крыло, и толщины формирующейся каверны, а во-вторых, развиваются интенсивные колебания каверны и циркуляции скорости вокруг крыла. Однако, в этих работах не указывалось на резонансный характер этого режима обтекания и не была дана физическая схема, описывающая причину резонанса и позволяющая описать нелинейные вихревые структуры, формирующиеся при возникновении этого режима. Отметим, что так же, как и в случае движения крыла вблизи свободной поверхности весомой жидкости, решение квазилинейной задачи здесь может быть представлено в виде системы линейных интегральных уравнений относительно двух функций - вихревой интенсивности, распределенной по поверхности крыла и каверны, и распределения источников, интенсивность которых характеризует распределение толщин профиля и каверны.

    Как и в случае крыла, движущегося вблизи свободной поверхности воды, эта система имеет бесконечное множество сингулярных решений для распределения источников и вихрей, при выборе одного из которых используется  два дополнительных условия: условие Жуковского – Чаплыгина - Кутта  для вихрей и условие замыкания - для каверны. Именно эти два условия определяют нелинейную взаимную связь между обеими искомыми функциями, одна из которых характеризует относительную толщину каверны, а другая - распределение циркуляции по крылу и его подъемную силу. Из рассмотрения аналитического и численного решения этой задачи следует, что, когда длина каверны приближается к хорде крыла, происходит утолщение каверны, приводящее к увеличению погиби средней линии системы профиль-каверна, что, в свою очередь, увеличивает циркуляцию вокруг этой системы и вновь утолщает каверну. Если рассмотреть теоретическое решение стационарной линейной задачи в случае, когда длина каверны в точности равна хорде крыла, то взаимное усиление приводит в линейной постановке задачи при заданном малом угле атаки к неограниченному росту толщины каверны и коэффициента подъемной силы крыла. Расчёты каверны в этом случае, выполнены М.А. Баевой [121].  Решение соответствующей нелинейной задачи, хотя и не дает бесконечных величин толщины каверны и коэффициента подъемной силы, но указывает на существенный рост обоих указанных параметров.

    Удивительным является тот факт, что даже при нулевом угле атаки пластины теоретически существует такое нелинейное циркуляционное течение, когда около пластинки возникает присоединённая каверна, плавно замыкающаяся на задней кромке крыла. Подробный теоретический анализ такого течения выполнен М. А. Басиным и А. В. Баландиным [31].

    Таким образом, анализ квазилинейной задачи, так же как и для крыла, движущегося вблизи границы раздела сред, указывал в случае переходного режима кавитации на те же признаки, которые были обнаружены ранее при исследовании гидродинамических характеристик крыла, движущегося вблизи свободной границы. 

 

 

5. Рождение концепции вихре-волнового

 и структурного резонанса.

 

Результаты анализа перечисленных выше явлений показали, что аномальные режимы несимметричного обтекания тел наблюдаются в случае сравнительно узкого диапазона изменения безразмерных управляющих параметров, например, числа Фруда или числа кавитации. При этом в критическом режиме оказываются близкими некоторые геометрические характеристики потока: длина судна и половина длины поперечной присоединённой волны, хорда крыла и длина полуволны, формирующейся на её поверхности, хорда крыла и длина присоединённой каверны. Исключением, казалось бы, был режим движения крыла вблизи экрана. Однако решение соответствующей аэродинамической задачи указывало на то, что влияние экрана на аэродинамические характеристики крыла эквивалентно влиянию симметрично расположенного относительно экрана крыла той же геометрической формы. И здесь аномальное течение возникает как результат взаимодействия двух симметрично расположенных крыльев, имеющих одинаковые размеры.

Эти результаты указывали на возможную аналогию с интенсивно изучавшимися в этот период волновыми резонансами. Была высказана гипотеза о том, что все указанные явления имеют резонансную природу. Предполагалось, что резонансы этого типа могут возникать при взаимодействии между основным потоком, формируемым при движении тел в неоднородной среде, и диспергирующими внутренними волнами, а также другими типами волновых и вихревых движений.

    В процессе обоснования предложенной гипотезы была создана единая классификация волновых движений, вихрей, грибовидных (дипольных) структур и транспортно - информационных систем, основанная на их волновой природе  и отражающая бифуркационные процессы перехода структур и систем одного более низкого класса в другой. Решён ряд модельных задач взаимодействия тела с вихрями и волнами в резонансном режиме. Проведены дополнительные экспериментальные исследования, позволившие определить особенности аномальных явлений, возникающих при резонансном взаимодействии движущихся тел с окружающей средой. Результаты этих исследований были опубликованы в ряде статей и монографий [38-41, 157-179]. В настоящее время разрабатываются математические модели, позволяющие определить общие условия возникновения вихре - волнового и структурного резонанса при движении твёрдых тел и деформируемых объектов в сплошной среде .

Для того, чтобы провести аналогию с открытыми ранее волновыми резонансами, необходимым оказалось расширить представление о волновых движениях, связанных с перемещением твердых тел в жидкостях, проанализировать с новых позиций формирование циркуляции на поверхности крыла и вывести на основе этих результатов критерии резонансного взаимодействия тел с линейными и нелинейными волнами, возникающими в сплошной среде.

Амплитуда волн, формирующихся около крыла, движущегося вблизи свободной поверхности весомой жидкости в аномальном режиме, даже при достаточно малых величинах углов атаки, относительной кривизны профиля и относительной толщины крыла, рассчитанная в соответствии с линейной теорией, оказывается выше предельных нелинейных волн. Попытки расчёта нелинейных волн для этого режима численными методами, выполненные американскими авторами [126], а затем В. Г. Щигуновым [139], показали, что существующие методы решения нелинейных задач не дают устойчивой картины течения, то есть появляются разрушающиеся волны. Отсутствие аналитических и численных методов полного расчёта параметров обнаруженного режима течения предопределило необходимость дополнения расчётных методов непосредственного решения задач качественными методами анализа как физических причин самого резонансного явления, так и его нелинейных последствий. Тем более, что предварительные экспериментальные исследования обтекания крыла в обнаруженном режиме показали, что при взаимодействии крыла со свободной поверхностью формируются отсутствовавшие при других режимах вихре - волновые структуры, изучение которых требует специальных методов исследования.

В последние годы интенсивно развиваются новые качественные методы исследования нелинейных динамических систем и волновых процессов. Проанализирована связь между ударными и солитонными волнами, автоволнами, диссипативными структурами и режимами с обострением и обычными линейными волновыми явлениями. Возникла новая наука, синергетика, изучающая условия самоорганизации нелинейных систем (см., например, [8, 181,184].)

Осуществлённая нами в рамках синергетических исследований классификации волн, вихревых, грибовидных и древовидных структур, а также транспортно-информационных систем [31], [40-46] позволила рассматривать движение твердого тела в жидкости как особую форму нелинейной поверхностной уединенной волны, перемещающейся относительно частиц жидкости со скоростью, равной скорости движения тела.

Основным геометрическим параметром этой нелинейной волны является габаритный размер тела в направлении перемещения. Особенность рассматриваемой волны состоит в том, что вблизи границы твердого тела наряду с полем скоростей и давлений формируется также область завихренности, образующая при определённых условиях тонкий пограничный слой.

Одновременно в сплошной среде, в которой движется тело,  существуют условия для возникновения собственных, присущих данной среде волновых движений. Параметры этих волн удовлетворяют обычно некоторым дифференциальным уравнениям в частных производных. Воздействие движущегося твёрдого тела на такую среду эквивалентно введению некоторых распределённых волнообразующих особенностей, Как было отмечено выше, при постоянной поступательной скорости движения около тела формируется практически неизменная волновая картина, перемещающаяся со скоростью его движения. Формирование такой картины носит резонансный характер. Движущееся тело резонансно стимулирует отбор из всего множества возможных свободных волн такой их совокупности, которая может переем ещаться, не меняя своей структуры со скоростью движения тела. Аналогичное явление наблюдается при натекании потока на препятствие. Эти явления многократно наблюдались и ранее и условие равенства скоростей движения тела и присоединённых к нему волновых картин существенно использовались для эффективного решения прикладных задач, однако мало внимания обращалось на резонансный характер этого процесса. Этот относительно простой тип структурно – волнового резонанса назван нами резонансом по скорости.

Однако амплитудные характеристики волновых картин, резонансно присоединённых к движущемуся телу, и связанное с ними волновое взаимодействие, как показывают расчётные и экспериментальные данные, существенно зависят при одной и той же скорости движения от габаритного размера движущегося тела в направлении его движения. Когда этот размер становится соизмеримым с размерами присоединённой волновой картины, наблюдается рост амплитуды этой волновой картины и резко изменяется характер взаимодействия тела и сплошной среды. Мы назвали этот процесс структурно - волновым резонансом по скорости и длине волны. С наших современных позиций и это явление может рассматриваться как резонансное, так как усиление интенсивности волн, вызванных движением тела, в данном случае также носит  характер волнового резонанса. При постоянной скорости движения  тело захватывает с собой волну (или спектр волн заданной формы) с длиной, однозначно определённой скоростью движения тела -возникает резонанс по скорости. При этом амплитуда захваченной волны пропорциональна коэффициенту Фурье в интеграле Фурье, которым может быть представлено граничное условие на поверхности тела. Этот коэффициент максимален, когда длина тела близка к длине резонансно захваченной телом волны [34, 142,182]. Тем самым, вследствие двойного резонанса по скорости и длине волны при поступательном движении тела наблюдается более интенсивное волнообразование и максимальные значения сопротивления движению тела.

Существенно меняется интенсивность резонансного взаимодействия при движении в сплошной среде несимметрично обтекаемых тел – крыльев.

Вблизи границ стационарно движущегося твердого тела в связанной с телом системе координат обычно имеются, как минимум, две так называемые “критические точки” (седловые точки или точки изменения знака завихренности), то есть точки, в которых интенсивность зав ихренности, образующейся вблизи поверхности тела, имеет нулевое значение. В этих точках, вблизи которых скорость жидкости в области незавихренного течения близка к скорости движения тела (скорости волны), возможно появление неустойчивости вихревого движения. Вблизи этих зон создается условие для возникновения двойных спиральных вихрей («вихревых ударных волн первого рода»). Другим источником особых зон потока являются районы большой кривизны, угловые точки или линии скачка положения касательных плоскостей к поверхности тела. В этих районах происходит явление, обычно называемое отрывом пограничного слоя, связанное с тем, что зона присоединённой к телу завихрённости утолщается и начинает формироваться двойной спиральный вихрь. Приближенное математическое описание возникновения подобного рода структур было дано М.А. Басиным и Н. Ю. Завадовским в работе [40], в которой удалось установить аналогию между формированием двойного спирального вихря на границе потенциального течения жидкости и ударной волной, что явилось причиной названия такого рода структур - “вихревые ударные волны первого рода”. Благодаря диффузии завихрённости спиральные вихри превращаются в концентрированные вихревые структуры - вихревые пузыри. Образование вихревых пузырей характеризует возникновение специфической, не исследовавшейся ранее подробно формы потери энергии в вязкой жидкости, связанной с взаимодействием конвекции и

диффузии завихренности внутри вихревого пузыря.

     В случае несимметричного обтекания крыла образование вихревой ударной волны первого рода (вихревого пузыря) вблизи острой задней кромки  на засасывающей поверхности крыла приводит, благодаря нелинейному взаимодействию с основным потоком, к появлению новых слоев раздела («вихревых ударных волн второго рода»). Они возникают благодаря перезамыканию (слипанию) существовавших до этого раздельно вихревых пограничных слоев, сходящих с нагнетающей и засасывающей поверхностей крыла.

 В результате слипания происходит отделение вихревого пузыря от движущегося тела и формирование новой вихревой структуры, названной нами выше «вихревой нейтральной грибовидной структурой». Она состоит из присоединенной замкнутой вихревой волны, движущейся вместе с крылом, отделившегося от неё разгонного вихря (вихревой ударной волны первого рода) и соединяющей их тонкой двухслойной вихревой пелены (вихревой ударной волны второго рода) в двумерном случае. При обтекании крыла конечного размаха вихревая пелена окаймляется постоянно формирующимися концевыми концентрированными вихревыми пузырями (вихревыми ударными волнами первого рода).

В результате этого процесса в системе координат, связанной с крылом, вблизи него реализуется почти установившееся течение с циркуляцией, определяемой из условия Жуковского – Чаплыгина - Кутта на задней кромке [147-150].

Плавность обтекания острой задней кромки крыла поддерживается за счёт особого типа гидродинамической устойчивости, аналогичного интенсивно изучаемому в настоящее время режиму самоорганизованной критичности. Любое нарушение этого условия приводит к возникновению «ударного» обтекания задней кромки и появлению вблизи неё вихревых ударных волн первого рода, отделение которых от поверхности крыла, изменяя циркуляцию, вновь делает течение вблизи острой задней кромки плавным. Этот процесс позволяет практически без затрат энергии и безинерционно обеспечивать за счёт управления углом атаки крыла или его формой изменять поперечные силы, действующих на крыло, и использовать крыльевые устройства в качестве несущих конструкций и управляющих элементов самолётов, космических аппаратов, экранопланов, дельтапланов, парашютов и судов различных типов, а также при создании лопастных механизмов: движителей, вентиляторов, насосов, турбин, ветровых электростанций. Природа также широко использует крылья в создаваемых ею «конструкциях». Птицы, рыбы, некоторые млекопитающие, насекомые используют крылья в качестве несущих и управляющих элементов и движителей. Кроме того, любой объект, несимметрично движущийся в газообразной и жидкой среде, становится крылом, и все вышеприведённые утверждения могут быть применены и к нему.

Изложенная выше схема формирования условия плавного обтекания угловой задней кромки крыла использована М. А. Басиным и  И. Г. Шапошниковым для разработки нелинейной модели обтекания крыла в рамках невязкой жидкости, обобщающей гипотезу Жуковского- Чаплыгина- Кутта на случай произвольного нестационарного движения крыла [143]. Эта модель в какой-то мере является аналогом модели бифуркации рождения цикла в теории автоколебаний конечномерных динамических систем [75].

Ранее из подобных волновых представлений о формировании циркуляции на поверхности крыла исходил один из основоположников теории крыла – Ф. Ланчестер [144-146]. Однако, в дальнейшем, благодаря успехам, достигнутым в локальном анализе характеристик крыльев, основанном на постулате Жуковского – Чаплыгина - Кутта [146-150],  волновому характеру обтекания крыла внимания уделялось мало.

Значительно усложняется картина течения при движении крыла в неоднородной сплошной среде, в частности, вблизи свободной поверхности жидкости, которая является новым, дополнительным источником волновых движений. Обычно гравитационные волны малы, и для их анализа достаточно применения результатов линейной теории. Однако, при увеличении амплитуды и энергии гравитационных волн в районе их гребней интенсифицируется вихревое движение, и локальная скорость в этой зоне становится близкой к скорости перемещения волны. Предельной теоретически возможной стационарной гравитационной волной на глубокой воде является волна Стокса с  (- высота волны, - её длина), в вершине которой, как и при обтекании движущегося твердого тела, образуется критическая точка, скорость жидкости в которой равна скорости волны. Дальнейшее увеличение энергии гравитационной поверхностной волны приводит к появлению в её вершине сверхкритических скоростей, формированию вихревых ударных волн, присоединенных к основной волне - к частичному или полному разрушению волн [49-55] .(разрушение поверхностной волны вследствие неустойчивости наступает несколько раньше).

Разрушение нелинейных гравитационных поверхностных волн, начиная с некоторых величин переносимой ими энергии, становится во многом эквивалентным развитию вихревых ударных волн при несимметричном циркуляционном обтекании тела. Здесь также устанавливается своеобразный «режим самоорганизованной критичности», прекрасно описанный поэтом [210] и вдохновивший многих художников. Таким образом, вихревое обтекание тела с формированием на его поверхности циркуляционного течения и поток, создаваемый гравитационными волнами, возникающими на поверхности жидкости, могут рассматриваться с единых позиций как нелинейные волны, связанные с деформацией или перемещением границ раздела сред.

При движении несущего тела вблизи границы раздела сред или в произвольной среде, в которой могут возникать волновые движения, при определённом соотношении между геометрическими характеристиками движущегося тела, скоростью его движения и дисперсионными свойствами сплошной среды может возникнуть третья форма вихре - волнового и структурного резонанса - вихре-волновой резонанс по скорости и размерам тела, присоединённой вихревой структуры и волновой картины, интенсивность проявления которого значительно превышает интенсивность двух первых форм вихре - волнового и структурного резонанса. Именно эта форма резонансных явлений приводит к аномально высокой интенсивности взаимодействия движущегося объекта с окружающей средой.

Четвёртой формой вихре - волнового и структурного резонанса является взаимодействие несущих тел между собой или со структурами, формируемыми при их движении. Примерами структурно-вихревого резонансного взаимодействия такого типа являются движение крыла вблизи экрана и переходный режим кавитации. В последнем случае взаимодействующими волновыми структурами являются несущее крыло и возникающая вблизи него присоединённая паровая или газовая каверна.

 

                                          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

                                                 Этюд 23

 

 Вихре-волновой и структурный резонанс. Концепция работает.

 

1. Основные параметры движущегося тела как уединённой волны

 

В соответствии с концепцией вихре - волнового и структурного  резонанса, предложенной для качественного объяснения аномальных явлений, обнаруженных при движении тел в неоднородной сплошной среде, твёрдое или деформируемое тело, движущееся в сплошной среде, отождествляется с эквивалентной уединённой волной (телом – волной)  [31]. При этом скорость волны, эквивалентной телу,  принимается равной скорости движущегося тела :

 

,                                             (5.1)

 

а длина эквивалентной волны определяется по приближённой формуле:

,                                           (5.2)

 

где - размер тела в направлении движения.

Коэффициент  зависит от формы обтекаемого тела и может определяться, в случае отсутствия полного теоретического решения конкретной задачи взаимодействия, эмпирически. Теоретические расчеты обтекания симметричных и несимметричных тел и крыльев дают основания предварительно определить наиболее вероятный диапазон изменения этого  параметра  ,  хотя в некоторых случаях его значение может лежать и вне этого диапазона.       Основанием для принятой гипотезы могут служить рассуждения, приведённые Дж. Лайтхиллом при анализе волновой картины около препятствия на дне потока весомой жидкости [34]. Другим теоретическим основанием может служить анализ результатов замены симметрично обтекаемого тонкого тела системой источников с суммарной интенсивностью, равной нулю. Если считать, что эти источники расположены на линии, совпадающей с направлением движения тела, и имеют в первом приближении линейно изменяющуюся интенсивность, то разложение распределения источников в интеграл Фурье вдоль направления движения даст некоторую функцию от волновых чисел, максимум которой окажется в зоне длин волн, близких к длине обтекаемого тела. А именно эта гармоника формирует присоединенную волну в случае соответствующего выбора скорости относительного движения.

Волновое число эквивалентной волны определяется по формуле:

 

,                                          (5.3)

 

а частота эквивалентной волны –

 

.                                         (5.4)

 

2. Классификация вихре - волновых и структурных резонансов..

 

    Качественный анализ теоретических и экспериментальных данных и разработка новых математических моделей позволили создать классификацию резонансных процессов между движущимся телом и окружающей средой,  включающую:

1.   резонансное возбуждение движущимся (и (или) колеблющимся) телом или системой особенностей определённой волновой картины, включающей лишь один набор волн из возможного спектра волн в окружающей сплошной среде - резонанс по скорости и частоте;

2.   структурно-волновой резонанс по скорости и размерам, когда размеры тела соизмеримы с размерами присоединённой волновой системы;

3.   вихре - волновой резонанс по скорости, размерам тела и параметрам вихревых структур, формируемых около движущегося несимметричного тела в среде, в которой возможно появление диспергирующих волн, границ раздела и вихревых структур, возникновение которого определяется дополнительным условием плавного обтекания кормовой части тела (постулатом Жуковского - Чаплыгина – Кутта), приводящий к резкому изменению циркуляции потока около тела, а следовательно, сил взаимодействия между телом и сплошной средой.

4.   резонансное взаимодействие через среду нескольких несимметричных тел, движущихся  в сплошной среде, или тел с границами раздела сред и (или) вихревыми структурами (структурный резонанс) .

    Два первых типа явлений были известны ранее и исследовались при решении различных прикладных задач. Однако не был достаточно чётко прояснён их резонансный характер. Третий и четвёртый типы вихре - волнового и структурного резонанса либо не изучались вовсе, либо не рассматривались ранее как резонансные явления.

    Указанные типы резонансов могут возникать при движении тел в средах, в которых  формируются диспергирующие волны, автоволны, границы раздела сред и фаз, а также  вихревые и грибовидные структуры различной природы или при обтекании препятствий , а также ниш и отверстий. К этому типу резонансов можно отнести также процесс взаимодействие квантовой частицы с потенциальной ямой или барьером, что позволяет применить концепцию вихре-волнового и структурного резонанса к исследованию процессов, происходящих в микромире и изучению явления самоорганизации при анализе нано-процессов. Однако для всех возможных разнообразных форм этого резонансного явления могут быть определены общие необходимые условия его возникновения и существования, знание которых позволяет предсказывать, находить и изучать и воссоздавать различные формы этого необычного феномена.

 

 

 

3.                                                                                                                                                                                                              Дисперсионные свойства сплошной среды.

 

Рассмотрим общий случай движения тела в сплошной среде (поле), внутренняя динамика которого описывается некоторым линейным или нелинейным оператором, воздействующим на полевые потенциалы. В среде, в которой движется тело, обычно справедливо дифференциальное уравнение в частных производных для основной функции распределения скалярного, векторного или тензорного параметра, определяющего  характеристики потока.

 

,                                              (5.5)

 

 где - некоторый линейный или нелинейный оператор. Этому оператору обычно соответствует определённый собственный спектр линейных и нелинейных волн или структур, между элементами которых существует система спектральных соотношений

 

,                                        (5.6)

 

где  и  частоты и волновые числа элементарных волн, которые могут быть возбуждены в сплошной среде.

Решая  последнее уравнение относительно , получаем

.                             (5.7)

Скорость перемещения элементарной волны определяется её длиной

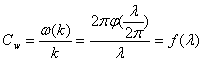.                          (5.8)

 

4. Резонанс по скорости.

 

При равномерном поступательном  движении тела картина волн, формирующихся вблизи тела, перемещается вместе с телом, оставаясь неизменной. Это широко известное явление имеет резонансную природу, так как движущееся тело формирует около себя устойчивую волновую картину только из тех волн, проекция скорости которых совпадает со скоростью движения тела. Оно было названо нами резонансом по скорости.

На основании условия резонанса по скорости может быть определена структура волн, присоединённых к телу, или в частном случае, одной резонансной присоединенной волны, что и было сделано рядом авторов для случая корабельных волн [34], [118].

    Волны других длин имеют скорости, меньшие или большие, скорости движения тела, и в случае двумерного обтекания уходят от тела вперёд и назад, не формируя устойчивой резонансной картины. При установившемся движении с телом  движется лишь одна резонансная волна или лишь одна волновая картина .

    В соответствии с предлагаемой концепцией основным необходимым условием структурно волнового резонанса по скорости является условие равенства скоростей тела и присоединённой волновой картины, что приводит к равенству:

                           (5.9)

 

 или

 

.                           (5.10)

   

Таким образом, в стационарном потоке за препятствием или впереди него формируется волновая картина, определяемая скоростным резонансом, в простейшем случае представляющая синусоидальную волну, волновое число которой определяется скоростью движения тела или скоростью набегающего на препятствие потока и спектральными характеристиками среды. В случае  сложных форм зависимости волнового числа от скорости потока, когда функция многозначна или бесконечнозначна, резонансная картина волн, присоединённых к движущемуся телу, может стать достаточно сложной, например, трёхмерная волновая картина при движении судна, описанная выше [34,110, 111, 118].

 

4.                                                                                                                                                                                                              Околозвуковое и сверхзвуковое движение тел.

 

Характерным является пример присоединённых ударных волн при трансзвуковом и сверхзвуковом движении тел в жидкости или газе. Дисперсия волн в этом случае практически отсутствует. Поэтому при скоростях, меньших скорости звука, резонансный режим по скорости не наступает. Присоединённых к движущемуся телу волн нет. Если скорость движения тела равна скорости звука, то функция становится в линейном приближении бесконечнозначной и наступает скоростной резонанс практически со всеми волнами звукового спектра. Потенциальная возможность резонансного роста амплитуд волн различной длины порождает присоединённую к движущемуся телу нелинейную ударную волну.

 В действительности, при скоростях, близких к скорости звука, за счёт нелинейных эффектов, наблюдается  дисперсия, что усложняет волновую картину около тела, но основная закономерность сохраняется.  При скоростях движения тел, больших скорости звука, скоростной резонанс обусловливает существование угла Маха при формировании присоединённых волн [211-214 ].

 

5. Движение тела на мелководье

 

В некотором смысле противоположная картина наблюдается при движении судна на предельном мелководье. В этом случае в жидкости существует предельная скорость диспергирующих волн, определяемая соотношением:

 

,                                   (5.11)

 где - ускорение силы тяжести, - глубина водоёма или толщина слоя воды. При приближении скорости судна, а следовательно, скорости присоединённой волны к дисперсионное соотношение для поверхностных волн вырождается, и волны всех длин приобретают скорость, близкую к предельной. Скоростной резонанс в этом предельном случае проявляется в формировании в носовой части движущегося судна мощной поперечной волны [215]. В случае, если скорость движения судна несколько превышает  предельную скорость волны, волновая картина практически полностью исчезает. Этот эффект был открыт в Англии в XIX веке. Вот что пишут по этому поводу Дж. Лайтхилл и цитируемый им Скотт-Рассел [34]:

«Некоторые интересные следствия вытекают из того факта, что скорость волн на воде глубины  не может превышать . Это означает, что если скорость потока , то не существует решения (уравнения для дисперсионного соотношения), описывающего волны с перпендикулярными направлению распространения гребнями. Препятствия общей формы ещё могут создавать волны с наклонными к направлению движения гребнями… С другой стороны, препятствие, близкое по форме к перекрывающему поток цилиндру и создающее значительные волны с гребнями под прямым углом к потоку, когда , не может породить такие волны, когда , и обычно создаёт слабые наклонные волны.

Аналогично, широкая баржа, почти перекрывающая канал, по которому она движется, испытывает внезапное понижение сопротивления, когда её скорость превышает . Главный член в волнообразующем сопротивлении … исчезает, и сохраняется только намного меньший член, обусловленный возникновением наклонных волн по бокам баржи.

Скотт Рассел писал в 1844 г.: «Насколько мне известно, это явление было случайно открыто на канале малых размеров Глазго - Ардроссан. Горячая лошадь, впряжённая в лодку Уильяма Хаустона, эсквайра, одного из владельцев предприятия, испугалась и понесла, волоча лодку за собой, и к своему удивлению, м-р Хаустон увидел, что пенящаяся кормовая волна, которая обычно опустошала берега, исчезла, и судно шло по воде сравнительно плавно с очень сильно уменьшенным сопротивлением. М-р Хаустон обладал практичностью и осознал коммерческое значение этого факта для компании канала, с которой он был связан». Он посвятил себя внедрению на этом канале судов, движущихся с такими высокими скоростями, как 9 миль в час, что влекло за собой «большое увеличение доходов владельцев канала».

    Этот же эффект был  использован проф. А. М. Басиным при решении ряда задач об оптимизации форм судов, движущихся на мелководье [215-220], а также А. М. Басиным, И. О. Веледницким, А. Г. .Ляховицким и Е. И. Степанюком, предложившими принципиально новые типы судов, движущихся со сверхкритическим скоростями в условиях ограниченного фарватера [221-228 ].

Подробный теоретический анализ изменения нелинейной волновой картины при  переходе через критическую скорость движения  на мелководье выполнен Д. В. Маклаковым [156]. Он показал, когда и при каких условиях нелинейность приводит к формированию за обтекаемым препятствием различных типов волновых движений: волн Стокса, кноидальных волн, солитонов.

Аналогичных резонансных явлений следует ожидать при обтекании потоком малой глубины местных выступов и заглублений на дне потока, над  которыми также возникает присоединённая волновая картина.

 

4.Структурно- волновой резонанс по скорости и продольному размеру.

 

 Другой волновой параметр, который может определять резонансное взаимодействие, это длина волны. Если длина волны, эквивалентной движущемуся телу, становится близкой к размерам присоединённой к движущемуся телу волновой картины, то амплитуды волновых и вихревых возмущений сплошной среды достигают максимального значения. Необходимым условием этой второй формы структурно- волнового резонанса является равенство в направлении движения тела длин волн, эквивалентных телу, и длин волн, захваченных движущимся телом или формируемыми им вихревыми или дипольными структурами.

 

.                                       (5.12)

 

Используя соотношения 

 

                                         (5.13)

 

и условие скоростного резонанса

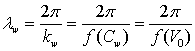,                            (5.14)

получаем  необходимое условие структурно- волнового резонанса по скорости и размерам:

 

;                                    (5.15)

 

или

.                                     (5.16)

 

Отсюда определяется зависимость скорости движения тела, соответствующей режиму структурно-волнового резонанса, от длины тела в направлении его движения и дисперсионных характеристик среды.

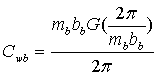                                   (5.17)

 

Здесь - скорость, при которой длина присоединённой к движущемуся телу волны равна длине волны, эквивалентной движущемуся телу.

Количество значений резонансной скорости при резонансах второго типа для данной длины тела определяется числом значений функции  при заданном значении длины волны.

 

 

5.Основной безразмерный параметр вихре - волнового и структурного резонанса.

 

    Проведённые рассуждения позволяют ввести в рассмотрение безразмерный параметр вихре - волнового и структурного резонанса по скорости и размерам:

 

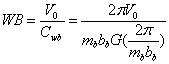.                                     (5.18)

 

В случае, если в среде движутся два тела или тело взаимодействует с вихревыми структурами, возникающими в сплошной среде и движущимися вместе с ним, например, с паровой или воздушной каверной при движении тела в жидкости, величина   определяется по более простой формуле

.                                        (5.19)

Здесь:

- длина вихревой структуры или каверны в направлении движения тела;

- поправочный коэффициент, который может быть, так же, как и для тела, принят лежащим в диапазоне .

Если форма движущегося тела и сопутствующей ему вихревой структуры близки или исследуется резонансное взаимодействие двух близких по форме тел, то величина резонансного параметра определяется по простой формуле

.                                              (5.20)

Необходимым условием существования вихре - волнового и структурного резонанса второго и более высоких классов является равенство скорости движущегося тела  и  - скорости, при которой длина присоединённой к движущемуся телу волны равна длине волны, эквивалентной движущемуся телу. Резонанс может наступить, когда безразмерный параметр вихре - волнового и структурного резонанса   станет равным единице

 

.                                              (5.21)

 

Пусть в некоторой сплошной среде имеются две взаимодействующие с ней структуры и пусть в течение некоторого промежутка времени они оказались на незначительном расстоянии друг от друга. Тогда, если их размеры близки, то мы вправе ожидать при их взаимодействии через среду (поле) проявления аномальных явлений, связанных с вихре - волновым и структурным резонансом. Тем самым, область поиска возможных проявлений этого явления существенно расширяется.

   

5. Горб волнового сопротивления тел в ограниченном фарватере как результат резонансного взаимодействия второго класса.

 

    Концепция вихре - волнового и структурного резонанса и эффективность введения специального резонансного числа подтверждается теорией и практикой проектирования судов и кораблей, движущихся  как в глубокой жидкости, так и в условиях мелководья. В этом случае дисперсионное соотношение для гравитационных волн в жидкости может быть записано в виде:

 

.                                (5.22)

 

Подставляя это соотношение в формулу (5.18), получаем:

 

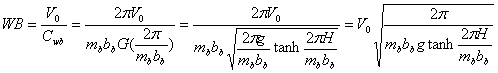.     (5.23)

 

Введём, как это принято при исследовании движения тел в весомой жидкости, безразмерное число Фруда по длине тела:

                                         (5.24)

 

и безразмерную относительную глубину жидкости

.                                          (5.25)

Тогда параметр структурно - волнового резонанса запишется в виде

 

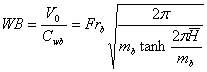 .                               (5.26)

 

В рассматриваемом случае резонансный параметр зависит от трёх безразмерных величин: числа Фруда по длине тела в направлении движения , поправочного коэффициента для эквивалентной волны  и относительной глубины водоёма (или потока) . Если относительная глубина потока стремится к бесконечности, то . Соотношение (5.26) перестаёт зависеть от относительной глубины бассейна и существенно  упрощается:

 

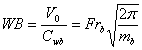.                                 (5.27)

 

В случае малой относительной глубины фарватера имеем :


  .                               (5.28)

Формула для  также существенно упростится и примет вид:

.                                   (5.29)

Резонансный параметр перестаёт зависеть от длины движущегося тела.

В общем случае, воспользовавшись условием резонанса по скорости и размерам , получим следующее соотношение:

 

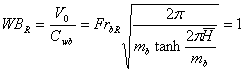                           (5.30)

 

Отсюда резонансное число Фруда по длине движущегося тела определяется формулой:

 

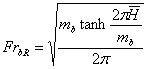.                                     (5.31)

 

С уменьшением относительной глубины бассейна среднее значение резонансного числа Фруда по длине тела уменьшается, одновременно сужается и диапазон резонансных значений этой величины. Однако, растёт  величина другого безразмерного резонансного параметра, числа Фруда по глубине водоёма, , формула для определения которого принимает вид:

 

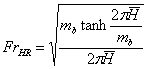.                                        (5.32)

 

 При , значение резонансного числа Фруда по длине тела определяется формулой  и стремится к нулю. При этом резонансное значение числа Фруда по глубине водоёма стремится к своему критическому значению , не зависящему от длины тела. Все длины волн становятся резонансными по скорости и резонансный эффект должен существенно усиливаться. В некоторых случаях целесообразно ввести новый параметр - число Фруда по глубине бассейна и длине тела. 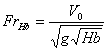, зависимость резонансного значения которого от параметров относительного движения определяется соотношением

 

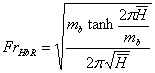                                  (5.33)

Хотя при предельных значениях глубин водоёма резонансные значения этого параметра стремятся к нулю, однако в широком диапазоне отношений глубины к длине тела его значения меняются мало .

  Эти выводы качественно подтверждаются результатами расчётов волнового сопротивления речных судов, выполненных А. Г. Ляховицким под руководством А. М. Басина [215] а также экспериментальными данными. Положение горба волнового сопротивления судов, для которых проводились расчёты и выполнялись модельные эксперименты для глубокой воды лежит в предсказанном исходя из концепции структурно-волнового резонанса диапазоне чисел Фруда по длине судна. С уменьшением глубины водоёма зона резонансных значений, соответствующих горбу волнового сопротивления сужается, тогда как сам горб, являющийся результатом резонансного взаимодействия всё большего числа компонент Фурье разложения формы тела с диспегирующими волнами сплошной среды, растёт по интенсивности. В пределе, когда резонансные значения числа Фруда по глубине стремятся к критическому значению, горб коэффициента волнового сопротивления оказывается максимальным, и характер зависимости его положения от скорости не зависит от длины судна.

Существование резонансных скоростей движения судов оказывает существенное влияние на оптимальную форму и конструктивные особенности судов, предназначенных для различных скоростных режимов [229]-[232

 

 

6.Резонансные явления при //движении тел в стратифицированной жидкости

 

Приведём ещё один пример использования резонансного параметра, который может служить основанием для развития нового направления исследований резонансного взаимодействия движущихся тел с неоднородностями сплошной среды. При горизонтальном движении тел в непрерывно стратифицированной сжимаемой жидкости или газе (океане или в атмосфере) в плоскости , где ось совпадает с направлением движения тела, а ось  направлена вертикально вверх, приближённое дисперсионное соотношение для продольных волн, направление движения которых совпадает с направлением движения тела, имеет следующий вид:[31, 34]

 

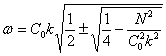,                                    (5.34)

 

где

 

;                       (5.35)

 

- равновесное распределение плотности по высоте, являющееся непрерывно убывающей функцией высоты,

-скорость звука невозмущённого течения при давлении  и распределении плотностей - равна отношению приращения давления к приращению плотности при постоянной энтропии.

При больших значениях  имеют место две значительно отличающиеся друг от друга частоты волн

 

.                                                 (5.36)

 

.                                                   (5.37)

 

В первом случае (5.36) скорость звуковой волны не зависит от её длины и резонанс по длине совпадает с резонансом по скорости, что резко сужает зону резонансных скоростей и расширяет зону резонансных длин  волн. Этот случай был кратко описан нами ранее при анализе резонанса по скорости для трансзвуковых течений около тел.

Второй случай (5.37) характеризует независимость волновой частоты от волнового числа, тогда как скорость волны обратно пропорциональна волновому числу и прямо пропорциональна её длине.

    Подставляя общее выражение для дисперсионного соотношения (5.34) в формулу для резонансного числа, получим

 

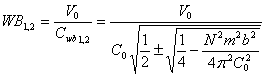                       (5.38)

 

или после преобразований

 

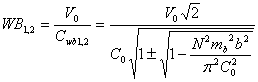.                       (5.39)

 

Рассмотрим отдельно значения .

 

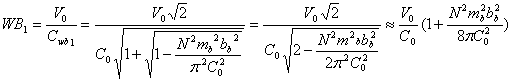.      (5.40)

 

Необходимое условие наступления вихре - волнового и структурного  резонанса примет вид

 

 .                                 (5.41)

Если ввести, как это обычно принято в аэродинамике, число Маха

                                            (5.42)

 то  резонансное  число Маха, определится по приближённой формуле

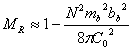                                    (5.43)

Формула (5.43) показывает, что значительные градиенты плотности в атмосфере могут привести к возникновению вихре - волнового и структурного резонанса и сопутствующих ему неблагоприятных воздействий на динамику летательных аппаратов не только при трансзвуковых, но и при околозвуковых скоростях движения. Это явление, если оно возникнет, может явиться причиной аварии летательного аппарата и поэтому потенциальная возможность его появления требует специального дополнительного изучения.

    Второй вариант резонансного числа в первом приближении может быть представлен в виде

 

.                                     (5.44)

 

Исходя из необходимого условия возникновения вихре - волнового резонанса

 

,                                 (5.45)

 

определяем величину резонансной скорости движения тела.

 

                                         (5.46)

 

 

    Из условия (5.46) следует важный вывод: скорость движения тела, соответствующая резонансному обтеканию,  уменьшается до нуля при . 

    Этот предсказанный теоретически результат может иметь такое же принципиальное значение, как и само явление вихре – волнового и структурного резонанса. В соответствии с ним, с уменьшением степени неоднородности жидкости резонансная скорость перемещения тела стремится к нулю. Следовательно, вихре – волновой и структурный резонанс по скорости и размерам теоретически возможен даже при очень малых неоднородностях сплошной среды и малых скоростях движения тела. Это физическое явление может быть использовано для индикации слабых неоднородностей в сплошной среде и на его основе могут быть сконструированы приборы, обеспечивающие такую индикацию.

Так как входящая в определение резонансного числа величина  является функцией от ускорения свободного падения , то природные гравитационные  аномалии  также могут повлиять на  условия возникновения вихре-волнового и структурного резонанса.

 

6. Вихре - волновой резонанс при движении крыла вблизи границы раздела сред . Численный и качественный анализ. Сопоставление теории с экспериментальными данными

 

. У несимметрично обтекаемых тел – крыльев имеется одна существенная особенность, отличающая их от симметрично обтекаемых тел. Благодаря условию плавного обтекания задней кромки таких тел (постулат Жуковского-Чаплыгина-Кутта) вокруг контура их продольного сечения формируется присоединённая вихревая структура с зависящей от геометрии тела и условий обтекания суммарной циркуляцией. Эта присоединённая к движущемуся телу вихревая структура, имеющая размеры, близкие к размерам тела, и являющаяся головной частью нейтральной грибовидной структуры [30-34 ], в свою очередь способна резонансно взаимодействовать как с самим телом, так и с диспергирующими волнами окружающей среды. При движении несимметричных тел в среде может возникнуть тройной резонанс, приводящий к аномальным изменениям не только волновой картины около движущегося тела, но и циркуляции вокруг несущих систем, а следовательно, к резкому изменению сил, действующих на тело.

Критериями, определяющими возможность появления такого резонанса, как и в случае резонанса второго типа, являются во-первых, равенство единице числа вихре - волнового и структурного резонанса и, во-вторых, асимметрия движущегося тела по отношению к направлению  скорости его движения или асимметрия обтекания тела.

    Подробное описание аномальных резонансных явлений  при движении крыла вблизи свободной поверхности воды, открытых группой исследователей под руководством одного из авторов, явившихся одним из оснований для введения в рассмотрение концепции вихре-волнового и структурного резонанса приведено выше, а также дано в монографии [31] .

    Попытаемся рассмотреть эти результаты с позиций концепции вихре-волнового и структурного резонанса. При движении крыла вблизи границы весомой жидкости имеются два типа вихре - волновых структур: вихревой пограничный слой на поверхности крыла и вихревой след за ним, а также диспергирующие поверхностные волны.

    Основным безразмерным управляющим параметром, определяющим условия возникновения вихре - волнового резонанса в случае движения крыла вблизи свободной поверхности весомой жидкости неограниченной глубины является число Фруда , где  - скорость движения,  - длина тела в направлении движения,  ускорение силы тяжести. Условием появления вихре - волнового и структурного резонанса при установившемся движении крыла, так же как и ранее, будем считать равенство скоростей тела и присоединенной гравитационной волны  и соизмеримость размеров присоединенной волны в районе тела с его длиной (длина тела должна составлять определенную часть присоединенной волны.  Приравнивая скорости движения и длины волн движущегося тела и свободной гравитационной волны в жидкости, получаем приближенное условие возникновения нелинейного вихре - волнового резонанса

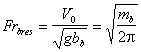.                                  (5.47)

Если предположить, что величина  должна изменяться в пределах от 1.0 до 2.0, то получаем: .

Именно в этом диапазоне чисел Фруда, как показали результаты представленных выше расчётов, наблюдаются основные резонансные явления при движении крыла в диапазоне относительных глубин . Сдвиг в критических значениях числа Фруда, соответствующих максимуму влияния на  относительной толщины профиля, объясняется различным характером резонансного взаимодействия.

При меньших значениях относительных глубин  характер волнового движения вблизи крыла несколько изменяется. Крыло, являясь источником возмущения, одновременно начинает играть роль локального дна, расположенного на малой глубине под свободной поверхностью воды. В этом случае характер поверхностных волн, их поведение вблизи крыла становятся все ближе к поведению волн на предельном мелководье, скорость которых в пределе соответствует величине , где - глубина воды, в данном случае - глубина погружения крыла. Именно поэтому с уменьшением глубины погружения происходит уменьшение резонансного значения числа Фруда по хорде крыла и увеличение со стремлением к единице резонансного значения числа Фруда по глубине. По той же причине в промежуточном диапазоне  относительных погружений крыла более предпочтительно в качестве наиболее стабильного параметра, определяющего вихре- волновой резонанс использовать число Фруда по хорде крыла и глубине его погружения. 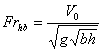, резонансное значение которого слабо зависит от относительного заглубления крыла .(смотри рис.4.2).

 

7. Качественный анализ нелинейных эффектов.

 

Концепция нелинейных вихревых ударных волн, разработанная при классификации волн, вихрей, структур и систем, кроме предсказания режимов движения, в которых следует ожидать резонансного взаимодействия тела с внешней средой, позволяет оценить также, в каких случаях и по каким причинам линейная теория может давать результаты, отличные от экспериментальных данных. На её основе можно также предсказать типы структур, которые  сформируются в результате резонансного взаимодействия.

Так, например, при анализе результатов расчётов гидродинамических характеристик подводного крыла по линейной теории было получено, что при резонансном значении числа Фруда над задней кромкой крыла должен круто подниматься склон кормовой волны, высота которой по расчетам может быть значительно выше предельной (см. рис 5). Как следует из концепции вихревых ударных волн и теоретических оценок, такая волна неустойчива и на вершине её должна формироваться вихревая ударная волна первого рода - концентрированный вихрь (или каскад пространственных концентрированных вихрей в виде брызг), диаметр которого при относительных глубинах, меньших , соизмерим с глубиной погружения крыла. Этот вихрь должен поглощать часть свободной границы, которая под действием сил тяжести и поверхностного натяжения теряет устойчивость, что приводит к тому, что при устойчивости в целом глобального вихревого и волнового движения течение внутри формируемой в кормовой части вихревой ударной волны становится хаотическим, однако волна продолжает оставаться над кромкой крыла, двигаясь вместе с ним. Между тем, как  следует из качественного анализа формирования вихревых ударных волн на крыле, подъёмная сила может значительно измениться только тогда, когда сформировавшийся вблизи задней кромки концевой вихрь (вихревая ударная волна первого рода), сходит с поверхности крыла (формирование вихревой ударной волны второго рода).

В резонансном режиме существует взаимное усиление роста циркуляции и роста кормовой волны за крылом. Разрушение кормовой волны на поверхности воды должно приводить к тому, что концентрированные вихри, образующиеся вблизи задней кромки крыла, не смогут отделяться от кромки, и рост циркуляции, а также энергии волны, формирующейся за крылом, прекратится. Таким образом, нелинейность при вихре - волновом резонансе должна приводить к тому, что очень большие величины, полученные на основании линейной теории при малых относительных заглублениях   не должны реализовываться. При этом результатом нелинейного взаимодействия может оказаться новая вихревая структура, формирующаяся вблизи задней кромки крыла, включающая в себя как элементы вихревую ударную волну, формирующуюся на свободной поверхности воды в результате разрушения волны, и концевой вихрь, возникающий вблизи задней кромки крыла.

 

8. Результаты экспериментального исследования проявлений вихре - волнового и структурного резонанса.

 

Результаты экспериментальных исследований, в которых был изучен   вихре-волновой резонанс при обтекании подводного крыла, сводятся  к следующему .

1.   Теоретически было предсказано, что при относительных скоростях движения крыла, лежащих в диапазоне чисел Фруда     для    и при ) должны возникать интенсивные резонансные явления. Анализ этих явлений , выполненный с позиций квазилинейной теории и концепции вихревых ударных волн показал , что при резонансных значениях чисел Фруда вблизи крыла возможно появление разрушающихся волн и формирование новых вихре - волновых структур. В опытовых бассейнах были проведены испытания крыльевого устройства прямоугольной формы в плане с удлинением  (- размах крыла) с плоско - выпуклым сегментным профилем продольного сечения (относительная толщина ) в широком диапазоне относительных глубин погружения и чисел Фруда. Испытания проводились при углах атаки . Особое внимание уделялось измерению гидродинамических характеристик и визуализации картины течения в критическом диапазоне чисел Фруда и относительных глубин погружения. Как и было предсказано теоретически, получены значительные отрицательные значения подъемной силы крыла даже при положительных геометрических углах атаки. При   и   наблюдаются значения  Как это и предсказано на основании концепции вихревых ударных волн, экспериментальные данные для   по сравнению с резонансными значениями, полученными по линейной теории, наоборот, сильно разошлись: они оказались значительно меньше расчётных.  Кроме того, анализ выполненных фотографий подтвердил теоретические выводы о формировании в указанном диапазоне чисел Фруда и относительных глубин погружения при всех исследованных углах атаки над задней кромкой крыла разрушающейся волны. При малых углах атаки экспериментально обнаружена носовая разрушающаяся волна иной формы, имеющая плоскую вершину, покрытую нестационарными “бурунами“. Носовая волна уменьшается с увеличением угла атаки, и при  практически исчезает: тенденция к исчезновению носовой волны с увеличением угла атаки подтверждается результатами расчетов по линейной теории . Вне указанного резонансного диапазона чисел Фруда при , как и предсказано расчетами , происходит качественное изменение картины течения. Вершина кормовой волны смещается назад и практически сразу исчезает носовая волна. С удалением от крыла присоединенной  кормовой волны резко увеличивается значение . Величина коэффициента подъёмной силы проходит через нуль и с дальнейшим увеличением скорости принимает положительные значения (если ). Течение вблизи крыла становится плавным с малыми волновыми деформациями на поверхности жидкости . При этом измеренные величины подъёмной силы крыла практически совпадают с данными, полученными по линейной теории. Предсказания о расхождении значений  между результатами линейной теории и экспериментом, основанные на концепции вихревых ударных волн первого и второго рода, качественно подтвердились . Эксперимент показал также существование новой . не изучавшейся ранее формы разрушения нелинейной носовой волны. Диапазон чисел Фруда и относительных погружений, соответствующий возникновению аномальных гидродинамических явлений в эксперименте практически полностью совпал с теоретически предсказанным диапазоном, что еще раз подтвердило основные положения на которых строился теоретический анализ .

 

 

8.Вихре-волновой резонанс в стратифицированной сплошной среде. Теоретические предсказания.

 

Другим характерным примером вихре-волнового резонанса является несимметричное движение тела вблизи границы раздела сред различной плотности. Если неподвижная среда (жидкость или газ) имеет внутреннюю границу раздела, и плотность нижней жидкости ., а верхней - ., то дисперсионное соотношение для внутренних волн записывается в виде:

 

или

 

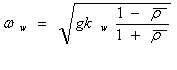,                                  (5.48)

 

где . Частоты и скорости волн, соответствующих одним и тем же волновым числам, оказываются тем меньше, чем больше отношение  и в случае, когда отношение плотностей стремится к единице, частоты и скорости перемещения внутренних волн стремятся к нулю. Воспользовавшись необходимым условием возникновения вихре – волнового и структурного резонанса и введя обобщённое денситометрическое число Фруда:

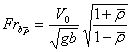,                                      (5.49)

легко показать, что при  условию возникновения вихре-волнового и структурного резонанса должно соответствовать соотношение:

 

                          (5.50)

или

 

.                             (5.51)

 

Если , то число Фруда , при котором возникает резонанс, также стремится к нулю. Этот теоретический результат, хотя ему может быть найдено разумное объяснение, и он соответствует ранее полученному соотношению для непрерывно стратифицированной жидкости или газа, является удивительным и имеет фундаментальное значение. Малые скачки плотности и малые изменения скорости движения тела могут привести, вследствие вихре - волнового и структурного резонанса, к значительным возмущениям и появлению новых вихре - волновых структур в стратифицированной среде.

Теоретические расчеты и экспериментальные данные по определению волнового сопротивления тел, движущихся вблизи границ раздела, подтверждают эту гипотезу (явление «мёртвой воды») [34]. Так как зона параметров движения, при которой возникает вихре - волновой резонанс в стратифицированной среде, очень узка, явление резонанса явно проявляется в природных явлениях редко. Однако, возмущения, связанные с возникновением этого явления, столь велики, что могут стать причиной аномальных природных явлений и аварий подводных аппаратов и самолётов.

    Одним из авторов совместно с Ю. В. Кафтанниковым теоретически исследована  третья форма вихре - волнового и структурного резонанса при движении крыла в стратифицированной весомой сплошной среде [31]. Как следует из результатов расчётов (рис. ), резонансные значения коэффициентов подъёмной силы слабо меняются с уменьшением скачка плотности сплошной среды, тогда как скорость, при которой возникает вихре - волновой резонанс, стремится к нулю. Малые скорости движения в слабо - стратифицированной среде вызывают существенные резонансные возмущения коэффициентов нормальных к направлению движения сил, действующих на движущиеся тела.

    Полученный теоретический результат имеет такое же принципиальное значение, как и само явление вихре - волнового и структурного резонанса, и требует экспериментального подтверждения.

    В случае получения соответствующих экспериментальных данных обнаруженный эффект может найти широкое применение при измерении с помощью использования эффектов, связанных с вихре - волновым и структурным резонансом, малых неоднородностей в сплошной среде, в том числе и вредных примесей, плотность которых отличается от плотности основной части среды. На принципе вихре - волнового и структурного резонанса может быть построен новый класс приборов, являющихся индикаторами слабых неоднородностей плотности и полевых потенциалов в сплошных средах

Кроме того, результаты расчетов показывают, что уменьшение неоднородности слабо изменяет воздействие крыла на амплитудные характеристики гравитационных волн, возникающих в среде, то есть относительная интенсивность резонансного воздействия падает незначительно. Нелинейные эффекты, связанные с формированием новых вихревых структур, должны сохраняться вплоть до чрезвычайно малых неоднородностей и чисел Фруда.

    Однм из авторов совместно с Н.В. Корневым был разработан  вихревой метод решения трехмерных уравнений Навье - Стокса, использование которого, по-видимому, позволит прояснить в будущем расчетным методом детали вихре - волновых резонансных явлений [162]-[168] .

    В последние годы большое внимание уделяется изучению волновых явлений в атмосфере и океане, где неоднородность по плотности и скорости течений вызывает широкий спектр диспергирующих волн, движущихся в различных направлениях. Кроме того, в неоднородной сплошной среде вследствие гидродинамической неустойчивости формируются нелинейные волны, а также вихревые и грибовидные структуры [82]. Взаимодействие этих волн и структур с движущимися телами должно вызвать широкий спектр вихре - волновых резонансных явлений рассмотренных выше типов, условия возникновения которых определяются на основании построения в каждом конкретном случае частной модификации резонансного параметра .

 

9. Движение крыла вблизи экрана как проявление четвёртой формы вихре – волнового резонанса. Биологические и технические приложения.

 

 

. Вихре - волновой и структурный резонанс может возникнуть и при взаимодействии несущих тел между собой и с границами среды. Наиболее известным примером аномального изменения гидродинаических характеристик несущего тела является движение крыла вблизи экрана. Как показано в большом количестве теоретических и экспериментальных исследований, обобщённых в ряде статей, монографий и в справочных материалах (смотри например [121]) движение несущего тела (крыла) вблизи твёрдой границы сопровождается аномальным ростом подъёмной силы крыла и резким падением индуктивного сопротивления. Этот эффект похож по своим проявлениям на явление структурного резонанса. И может быть объяснён  с позиций разрабатываемой концепции.

Резонансный характер этого режима может быть объяснён следующим образом. Влияние экрана на подъёмную силу крыла теоретически может быть заменено эквивалентным влиянием симметрично расположенного относительно экрана крылом.

При таком рассмотрении указанного течения мы находим объекты вихре – волнового и структурного резонанса – это два крыла, движущиеся с одной скоростью и имеющие одинаковые хорды, расположенные симметрично друг относительно друга. Если эти крылья рассматривать как две уединённые вихревые волны, то существуют все необходимые условия для вихре – волнового и структурного резонанса.

В случае двух крыльев, поступательно движущихся с одинаковыми скоростями на незначительном расстоянии друг от друга условие возможности появления вихре - волнового и структурного резонанса соответствует формуле (5.20)  

,                                         (5.52)

где - хорда того крыла. Теоретические расчёты показывают, что резонансное взаимодействие, приводящее к росту аэродинамического качества, максимально, когда крылья расположены симметрично друг другу относительно плоскости, параллельной направлению их движения и расстояние между крыльями стремится к нулю. Именно этот резонансный случай и эквивалентен с аэродинамической точки зрения движению крыла вблизи экрана. Следует обратить внимание ещё на одну особенность указанного резонансного режима. Подъёмная сила крыла при приближении к экрану растёт обратно пропорционально расстоянию до экрана или, что аналогично, расстоянию между крыльями. А подъёмная сила приближённо пропорциональна циркуляции крыла. Таким образом, два движущихся симметрично друг относительно друга крыла за счёт вихре - волнового и структурного резонанса формируют дипольную структуру, интенсивность которой при малых расстояниях между крыльями не зависит от величины этого расстояния. Отсюда можно сделать вывод о том, что хотя бы в некоторых случаях формирование дипольных (грибовидных) структур может явиться результатом вихре - волнового и структурного резонанса. Что подтверждает сделанный нами ранее на основе простейшей математической модели вывод о резонансном характере формирования грибовидных структур.

К широкому спектру приложений влияния экранного эффекта на несущую способность крыльев следует добавить ещё одно направление использования этого типа резонанса, а именно применение эффекта резонансного взаимодействия несущих систем к созданию принципиально нового компьютерного метода распознавания образов, который позволит осуществить распознавание одновременно как по глобальным, так и по локальным масштабам.

 Кроме того, возникает идея о том, что в самом общем случае процесс распознавания образов, то есть отбора среди многих возможных таких, которые соответствуют данному, может быть построен на принципе структурно- волнового или вихре - волнового и структурного резонанса.

.Более сложные резонансные явления должны происходить при обтекании несущих систем в жидкости малой глубины. Наряду с резонансными взаимодействиями с волнами на свободной поверхности крыло  резонансно взаимодействует с дном.

«Экранный резонанс» может значительно усилиться вихре-волновым резонансом крыла с гравитационными волнами при установке несущих конструкций в потоке малой глубины. Такие конструкции могут служить мощными волнопродукторами либо волногасителями, а также основными элементами волновых электростанций

Возникающий здесь резонанс, четвёртого порядка может привести к гигантской концентрации энергии и его использование позволит построить новые конструкции,  например, возбуждающие и гасящие энергию волн, в том числе и волн цунами.

 

9. Качественный анализ кавитации подводных крыльев в режиме вихре - волнового и структурного резонанса.

. 

Ещё более необычный эффект, который также может быть отнесён к структурно - вихревому резонансу четвёртого типа, был подробно исследован нами при кавитационном обтекании подводных крыльев и лопастей гребных винтов быстроходных судов.

Многочисленные теоретические и экспериментальные исследования  показали, что именно в этом режиме кавитационного обтекания крыльев наблюдаются аномальные явления, связанные со значительным ростом подъёмной силы крыла и толщины каверны, приводящие к потере устойчивости и интенсивным колебаниям каверны с формированием вихревого следа, обладающего универсальными частотными характеристиками, не зависящими от формы профиля и угла атаки крыла.

    Для того, чтобы применить к рассматриваемому случаю качественный анализ, основанный на теории вихревых ударных волн, и концепции вихре-волнового и структурного резонанса, рассмотрим с волновой точки зрения паровую или воздушную каверну, присоединенную к движущемуся телу. Формирующаяся около тела присоединённая каверна, заполненная газом или паром, с деформируемой границей раздела плотности и фаз с позиций разработанной классификации нелинейных волновых движений, вихревых и грибовидных структур и транспортно-информационных систем, так же, как и твердое тело, может рассматриваться в качестве поступательно движущейся уединённой волны, скорость которой равна скорости тела (тем самым первое условие вихре - волнового и структурного резонанса для присоединенных каверн уже выполнено), а длина которой однозначно связана с длиной каверны :

 

.

 

    При этом с достаточной степенью достоверности (вследствие аналогичной геометрии) можно считать, что коэффициент  для движущегося в жидкости тела и  для формирующейся около него каверны равны между собой .

Поэтому в данном случае необходимое условие возникновения вихре- волнового и структурного  резонанса, имеющее в общем случае вид,

значительно упрощается и принимает форму

,

что полностью соответствует условию резкого роста амплитуд обеих введенных нами в рассмотрение нелинейных волн, полученному при решении квазилинейной задачи. Источники определяют толщину каверны, т.е. амплитуду нелинейной волны, ей соответствующей, а циркуляция, в соответствии с концепцией вихревых ударных волн первого и второго рода, определяют амплитуду присоединенной к телу циркуляционной волны, являющейся головной частью формирующейся при движении крыла грибовидной структуры.

    Концепция вихревых ударных волн позволяет, как и в случае движения крыла в неоднородной сплошной среде, не только предсказать условия возникновения вихре - волнового и структурного резонанса, но и построить схематизированную картину нелинейного вихре - волнового и структурного взаимодействия, указать на отличие реальной картины течения от предсказанных по квазистационарной теории и качественно проанализировать новые структуры, которые получаются в результате резонансного взаимодействия.

    Резонанс должен приводить не только к увеличению амплитуд обеих взаимодействующих волн: каверны и циркуляционной волны около крыла,-  но и к совместной глобальной потере ими устойчивости, (аналогичной бифуркации рождения цикла в обычных динамических системах) в результате которой формируются периодически возникающие грибовидные структуры, создающие за кавитирующим крылом кармановскую дорожку, основные параметры которой определяются размерным резонансным параметром - хордой крыла. Возникают автоколебания каверны и нелинейные автоволны в виде сложной системы, головную часть которой представляют резонансно взаимодействующие крыло и каверна, движущиеся со скоростью движения тела, а хвостовую- кармановская дорожка связанных грибовидных структур, формирующихся из пограничного слоя на поверхности крыла и свободной границы каверны).

    Если проанализировать качественно картину развитой кавитации за телом (двумерное течение), то можно выделить три основных типа нелинейных волновых структур: расположенное впереди движущееся поступательно со скоростью  твердое тело, присоединенную к нему деформируемую, заполненную газом или паром каверну и след, который можно схематизировать кармановской дорожкой связанных грибовидных структур.

    Границы каверны, которые могут считаться также поверхностями скачка завихренности, принципиально не могут формировать установившегося течения, так как в этом случае в хвостовой части должна была бы существовать седловая точка, а жидкость вливалась бы внутрь полости, пока не заполнила бы её .

В действительности, тенденция к возвратному течению жидкости внутрь каверны в хвостовой её части существует. Благодаря ей внутри каверны формируются области завихренности в паровой (газовой ) фазе. Сама граница каверны окаймляет область, занятую завихрённой сплошной средой. Однако, стационарная картина течения неустойчива, и периодически происходит формирование вихревых структур, в результате чего в следе за телом периодически формируются связанные свободные грибовидные структуры - кармановская дорожка свободных вихрей.

    Собственная скорость перемещения структур кармановской дорожки отлична от скорости перемещения тела и каверны. Кроме указанных выше трех типов вихре - волновых структур существует переходная зона, в которой происходит периодическое формирование грибовидных структур кармановской дорожки.

    При увеличении длины каверны, благодаря большему влиянию пространственности течения и поперечной неустойчивости крупные вихревые структуры становятся менее интенсивными. Переходная зона занимает все меньшую относительную часть каверны и, находясь вдали от тела, оказывает все меньшее влияние на колебание его гидродинамических характеристик. Структура и основные размеры формирующейся кармановской дорожки определяется в случае развитой кавитации поперечным размером каверны  в хвостовой её части, а точнее говоря, связанной с этим размером амплитудой изменения длины каверны за время формирования очередного периода кармановской дорожки. Именно этот параметр, в соответствии с концепцией вихревых ударных волн, определяет временные и пространственные масштабы формирующихся грибовидных структур, топологическая картина которых одинакова как при обтекании плохообтекаемых тел, так и при обтекании тел с развитыми кавернами. Именно этим объясняется близкое к постоянному значение числа Струхала формирования кармановской дорожки, построенного по характерному размеру тела или каверны, которые её формируют.

    В случае развитой кавитации угол атаки обтекаемого тела лишь изменяет относительную толщину каверны и увеличивает частоту формирования кармановской дорожки. При малых углах атаки толщина каверны при постоянной длине практически линейно зависит от угла атаки, а следовательно линейно от этого параметра зависит и период формирования кармановской дорожки .

    Несколько иную картину можно представить при качественном анализе с позиции концепции вихревых ударных волн частичной кавитации на тонком профиле крыла, поставленном под малым углом атаки .

    При больших значениях числа кавитации и малых углах атаки в кормовой части профиля сечения крыла формируется вихревая ударная волна второго рода с разгонным вихрем, вихревой пеленой и образующейся на крыле циркуляцией, величина которой определяется с помощью введения гипотезы Чаплыгина- Жуковского.

    Вблизи носовой кромки профиля также образуется присоединенная вихревая ударная волна первого рода - концентрированный вихревой пузырь, размеры которого обычно невелики по сравнению с размерами крыла. Существуют такие углы атаки и числа Рейнольдса, когда вихревой пузырь, благодаря влиянию вязкой диффузии и структуры потенциального внешнего потока оказывается практически стационарным.

    Именно  такая модель теоретического расчета ламинарных и турбулентных пузырей заложена в расчетных схемах, используемых в настоящее время различными авторами. .

    В зоне существования малых вихревых пузырей, расположенных обычно вблизи передней кромки крыла, и формируются частичные присоединенные каверны. Эта гипотеза положена Э.Л. Амроминым и А.Н. Ивановым  в основу предложенной ими теоретической модели формирования присоединенных каверн при исследовании масштабного эффекта возникновения кавитации, которая в настоящее время интенсивно развивается Э. Л. Амроминым. Кавитационный пузырь, так же, как и формирующий его вихревой пузырь, первоначально является стационарным, и его возникновение практически не сказывается на суммарных гидродинамических характеристиках крыла. Уменьшение числа кавитации приводит к росту размеров каверны. Наконец, наступает такой момент, когда сил поверхностного натяжения и вязкостных сил уже недостаточно для преодоления тенденции к возникновению неустойчивости в хвостовой части каверны. В этом районе начинает формироваться возвратное течение, которое образует периодически отделяющиеся от основной каверны полые вихревые пузыри - каверны и образующиеся в пограничном слое вихревые пузыри противоположного знака, интенсивность которых благодаря влиянию трения оказывается ниже, чем интенсивность сходящих сверху полых вихревых пузырей. Это несоответствие циркуляций полых и пристенных вихревых структур компенсируется изменением циркуляции крыла в целом, что, в свою очередь, приводит к периодическому формированию концевых вихрей вблизи задней кромки крыла. Таким образом, с крыла в режиме частичной кавитации также сходит кармановская дорожка вихревых (грибовидных) структур, причем  верхний ряд представляет собой след от колеблющейся каверны, а нижний - ряд вихрей, сходящих с задней кромки крыла. Основное отличие этой кармановской дорожки от той, которая возникает из развитой каверны, заключается в том, что нижние вихревые структуры сходят одновременно не с теми вихревыми структурами, которые вызвали их появление, а сдвинуты по отношению к ним в пространстве. Между верхними и нижними вихрями до схода с крыла отсутствует непосредственное взаимодействие. Кармановская дорожка как бы расщеплена в пространстве и во времени (её верхние и нижние структуры не взаимодействуют между собой).

    Как показывают теоретические расчеты, начиная с относительной длины каверны , возникает резонансное взаимодействие параметров каверны с циркуляционным течением вокруг крыла, которое теоретически проявляется в неограниченном росте относительной толщины каверны и циркуляции крыла . Исходя из концепции вихревых ударных волн, можно также предсказать, что одновременно с ростом амплитуды стационарных волн: толщины волны - каверны и циркуляционной волны около движущегося тела ,- должен наблюдаться нелинейный вихре - волновой резонанс между вихревыми ударными волнами, формируемыми каверной и крылом, на котором возникает периодически изменяющаяся подъемная сила. При этом, если при малых длинах каверны возникала несинхронизированная кармановская дорожка вихрей, параметры которой зависят от ширины каверны , то в резонансном случае должна формироваться единая резонансная кармановская дорожка, основные размеры которой при  определяются  хордой крыла .

    Колебания каверныв этом режиме должны быть максимальными и равными длине каверны.

    Теоретические исследования кавитирующих крыльев с длиной каверны, равной хорде крыла, позволили определить связь параметров резонансного режима кавитационного обтекания с формой профилей крыльев, предназначенных для бескавитационного и околозвукового обтекания, а также профилей, обладающих максимальным коэффициентом подъёмной силы. Построена универсальная диаграмма, охватывающая широкий класс профилей такого типа [121].

    Подробные экспериментальные исследования переходного режима кавитационного обтекания крыла выполнялись, начиная с середины 60-х годов. В ходе проведенной серии экспериментов на гидродинамических стендах и в кавитационных трубах измерялись мгновенные параметры течения около кавитирующего крыла. Исследовались зависимости от времени следующих относительных параметров течения: мгновенной длины присоединённой каверны , её ширины , протяженности зоны , в которой формируется вихревая ударная волна первого рода (длины обратной струйки ) , параметры структуры концентрированных вихревых объемов за движущимся крылом, являющихся результатом формирования вихревых ударных волн второго рода, образующихся в результате самопересечения границ каверны и вихревого насадка вблизи задней кромки крыла. Картина обтекания фиксировалась с помощью скоростной киносъёмки (1000 - 2000 кадров в секунду). Одновременно с визуализацией структуры течения измерялись мгновенные и средние значения подъемной силы и сопротивления крыла. Эксперименты проводились с крыльями различных профилей (, где - максимальная толщина профиля ,  -  хорда крыла) в диапазоне чисел кавитации , (где  давление в потоке перед крылом,

давление в каверне.)  и углов атаки . При этом главное вн

имание уделялось исследованию присоединенных каверн, начинающихся в

районе  носовой кромки крыла .

     Анализ полученных кинограмм позволил четко выделить резонансный

“переходный режим кавитационного обтекания крыла» . Как показали результаты

киносъемки, подтверждаются предсказания качественной модели , полученной на основании концепции вихревых ударных волн. Действительно, переходный режим обладает специфическими, свойственными только ему и универсальными для него

параметрами, определяемыми нелинейным резонансным взаимодействием

циркуляционного обтекания крыла с образованием вихревых ударных волн вблизи

задней кромки и течения с формированием вихревых ударных волн на границах

присоединенной каверны. Частота колебаний размеров каверны и суммарных сил,

действующих на крыло, когда максимальная длина каверны близка к хорде крыла, а следовательно, близки и их волновые частоты, определяется тем условием , что число Струхала  ,  где -частота колебаний . При этом амплитуда колебаний каверны приблизительно равна её длине и определяется резонансным параметром - хордой крыла . Основные параметры вихре - волновых структур в этом режиме кавитационного обтекания практически не зависят ни от формы профиля крыла , ни от его угла атаки, ни от числа кавитации.

Результаты экспериментов подтвердили предсказания, основанные на концепции вихревых ударных волн, о том , что картина течения в резонансном переходном режиме является результатом нелинейного резонансного взаимодействия кавитационного и циркуляционного обтекания крыла, которое приводит не только к взаимному увеличению толщины каверны и циркуляции на крыле , но и к синхронизации следа: формированию единой резонансной вихревой дорожки периодически образующихся вихревых ударных волн второго рода, верхний ряд которой является результатом формирования вихрей, отделившихся от границы каверны, а нижний ряд - следствием образования аналогичных вихревых сгустков в зоне вблизи задней кромки крыла. Соединяющая их вихревая пелена формируется как комплексная двойная граница раздела , частицы одной части которой ранее принадлежали границе каверны . а другой - пограничному слою на крыле.

 

17. О возможности обнаружения новых форм вихре-волнового и структурного резонанса

.

Вихре - волновой и структурный резонанс может проявиться и иметь свои специфические формы при любых относительных перемещениях произвольных тел и неоднородной сплошной среды, что дает возможность применять основные теоретические положения, позволяющие изучать это и другие нелинейные явления к судостроению и авиации, техническим производствам, химии, биологии, океанологии и метеорологии, физике и магнитной гидродинамике

Предсказанное теоретически и обнаруженное экспериментально явление  вихре- волнового и структурного резонанса вносит коренные изменения в существующие представления о взаимодействии различных объектов и окружающей их среды. Знание его природы и основных критериев возникновения позволяет теоретически предсказать, экспериментально обнаружить и объяснить не исследованные ранее аномальные режимы при движении тел в жидкости, газе и других сплошных средах.

Обнаруженное явление вихре - волнового и структурного резонанса может найти аналогии не только в гидродинамике тел, движущихся в неоднородной жидкости и газе, но и во всех тех случаях,. когда какая-либо жесткая или деформируемая система перемещается в неоднородной среде или происходит взаимодействие вихревых и грибовидных структур с окружающими их объектами или полем. Разработанная теория и выдвинутая концепция позволяют предсказывать условия, при которых следует искать аналогичные явления.

    Особого внимания заслуживает тот обнаруженный при изучении обтекания несущих тел теоретический результат, что при уменьшении степени неоднородности среды резонансные явления, почти не затухая, перемещаются в зону очень малых скоростей относительного движения тела и сплошной среды. Это позволяет использовать открытое явление как эффективный индикатор малых неоднородностей в среде и устройство управления, так как в этом случае при резонансе значительный эффект может быть достигнут без существенных затрат энергии.

Значение полученных результатов состоит не только в обнаружении и изучении нового неизвестного ранее класса резонансных процессов и вихре - волновых структур, но также и в том , что разработанная концепция и классификация волновых и вихревых движений позволяет предсказывать и обнаруживать неизвестные ранее формы вихре - волнового взаимодействия, создавать искусственно условия для возникновения этих явлений и разрабатывать способы их  предотвращения применительно к практическим задачам, а также создавать новые способы и разрабатывать новые конструкции,  которые могут найти применение также в различных областях техники и научных исследований. Широкое поле деятельности открывается также для изучения физических явлений и вихре - волновых структур, которые могут сформироваться при взаимодействии резонансного потока с другими типами волновых и колебательных движений.

Так как при исследовании биологических и социальных явлений наблюдается широкий спектр колебательных процессов и волновых структур, то концепция вихре-волнового и структурного резонанса может оказаться полезной при исследовании этих процессов, происходящих в различных масштабах, от клетки – до биосферы [65]. Автоволны, ревербераторы, диссипативные структуры, повсеместно возникающие в биологических объектах и во многих химических процессах, могут резонансно взаимодействовать с движущимися относительно них деформируемыми структурами, что должно привести к новым, не известным ранее, или известным, но не объяснённым,  особенностям аномального поведения. Именно в биологии, экологии и социальных науках могут быть найдены новые формы проявлений вихре- волнового и структурного резонанса. Предложенная концепция может явиться основой для объяснения не решённых ещё проблем, связанных с необходимостью объяснения размеров  и скоростей перемещения биологических объектов [75].

   

Заключение

 Обобщённая концепция вихре - волнового и структурного резонанса.

 

    Анализ полученных теоретических и экспериментальных результатов показывает, что нелинейное вихре - волновое резонансное взаимодействие циркуляционного вихревого течения около движущихся в неоднородной сплошной среде тел с волновыми движениями этой среды может приводить к появлению новых структур, представляющих собой взаимодействующие между собой нелинейные вихревые ударные волны и грибовидные структуры. Критерием для предсказания указанных аномальных явлений должны являться совпадение или кратность длин, скоростей или частот нелинейных периодических или одиночных волн, образующихся и взаимодействующих между собой.

    Концепция вихре - волнового и структурного резонанса может иметь далеко идущие теоретические обобщения, применение которых к различным частным случаям позволит предсказать и объяснить многие необычные явления, возникающие при взаимодействии структур и систем различной природы.

Приведённые выше примеры резонансного взаимодействия свидетельствуют о возможности существовании вихре - волновых и структурных резонансов при взаимодействии произвольных близко расположенных структур, находящихся в некотором общем поле, через которое они могут воздействовать друг на друга. Если структуры длительное время находятся вблизи друг друга, независимо от их перемещения относительно поля, то первое необходимое условие структурно-волнового резонанса – приближённое равенство скоростей нелинейных волновых структур, выполняется автоматически.

    Вторым необходимым условием структурного резонанса является равенство эквивалентных длин волновых структур. Это условие выполняется, когда соответствующие размеры взаимодействующих через поле структур близки.

    Для проверки  возможности существования и форм проявления структурно-волнового резонанса достаточно знать основные параметры поля, в котором расположены взаимодействующие структуры, основное уравнение, описывающее динамику поля, найти собственный спектр линейных и нелинейных волн, характеризующих это поле. Для большинства известных полей, особенно полей, описываемых линейными операторами, эта задача в той или иной степени решена (частные случаи таких решений рассмотрены нами выше). Для простейшего одномерного случая, когда поле удовлетворяет линейному уравнению в частных производных, эта задача решается в общем случае. Для более сложных случаев в математике и физике разработана теория линейных и нелинейных операторов [206].

    Воздействие структур на поле обычно описывается некоторыми интегральными операторами, характеризующими изменение поля под действием движущихся и излучающих структур. При этом не все параметры структур, воздействующие на поле, должны быть закреплены. В этом случае обратное действие поля на ту же самую или другую структуру может резонансно увеличивать (или уменьшать) не закреплённые параметры структуры. Условия резонанса остаются теми же. Совпадение длин и частот обобщённых волн и геометрическая близость структур между собой в течение некоторого промежутка времени. 

     В каждом частном случае может быть построено приближённое математическое описание взаимодействия и определены условия возникновения вихре - волнового и структурного резонанса при взаимодействии структуры и поля, а также при взаимодействии нескольких структур через поле.

    Как следует из выполненного теоретического анализа и экспериментального изучения некоторых проявлений вихре - волнового и структурного резонанса, резонансное взаимодействие приводит к отбору и усилению тех волновых частот и длин волн и структур, которые являются близкими для резонансно взаимодействующих объектов. Отсюда следует, что может оказаться справедливым не только утверждение о том, что вихре - волновой и структурный резонанс может быть использован для распознавания образов или обнаружения слабых неоднородностей в сплошных средах и полях различной природы, но также утверждение о том , что если такой отбор и такое усиление в каких-либо явлениях наблюдается, то сам этот факт может в ряде случаев служить сигналом, проявляющим вихре - волновой и структурный резонанс. При этом целесообразно искать не только резонансно - взаимодействующие объекты, но и их резонансные параметры. Такой подход позволит строить качественные теоретические модели вновь обнаруженных аномальных явлений.

    Остановимся теперь на том, как может проявляться вихре - волновой и структурный резонанс в сложных транспортно - информационных системах, часто представляющих собой иерархию волновых процессов с различными частотами и структур с различными масштабами, взаимодействующими между собой. Это внутреннее взаимодействие также осуществляется чаще всего резонансным образом, за счёт связей соседних уровней иерархии  и комбинационных резонансов, позволяющих перейти от заданных частот возмущения и масштабов (волновых чисел) к частотам и масштабам, определяемым соотношениями

 .

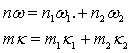    Возникновение вихре- волнового и структурного резонанса на одном уровне иерархии может резонансно же передаваться на нижележащие и вышележащие уровни системы. Вызванные резонансным воздействием возмущения могут нарастать и переводить систему в новое состояние (фазовый переход) или разрушить систему. 

При этом взаимодействие отдельно взятой подсистемы с другими подсистемами может носить двоякий характер. Это может быть ближнее взаимодействие, и тогда может проявиться и играть существенную роль четвёртая форма вихре-волнового и структурного резонанса. Это может быть также дальнее взаимодействие, и тогда резонансное  взаимодействие может осуществляться по схеме первой, второй и третьей форм вихре - волнового и структурного резонанса.

В обоих случаях резонансное взаимодействие может привести к появлению аномальных явлений и качественному изменению поведения как отдельных элементов или подсистем  или бифуркационному изменению системы в целом. 

Вихре - волновой и структурный резонанс может проявиться и иметь свои специфические формы при любых перемещениях произвольных структур в неоднородной сплошной среде, что дает возможность применять основные теоретические положения, позволяющие изучать это и другие нелинейные явления к судостроению и авиации, техническим производствам, химии, биологии, океанологии и метеорологии, физике и магнитной гидродинамике, экономике и других социальных процессах.

Предсказанное теоретически и обнаруженное экспериментально явление  вихре- волнового и структурного резонанса вносит коренные изменения в существующие представления о поведении течений около тел, движущихся в неоднородной сплошной среде. Знание его природы и основных критериев возникновения позволяет теоретически предсказать, экспериментально обнаружить и объяснить не исследованные ранее аномальные режимы при движении тел в жидкости, газе и других сплошных средах.

Открытие этого явления стимулирует создание и развитие новых методов теоретических и экспериментальных исследований вихревых движений в различных областях науки и техники.

Концепция вихревых ударных волн первого и второго рода, а также осуществлённое в связи с изучением открытого явления отождествление поля скоростей около движущегося тела и присоединенных следов и каверн со специфическими уединенными нелинейными волнами  используется для классификации нелинейных волновых движений и объяснения известных, но не изученных до конца нелинейных явлений , связанных с движением тел в жидкости: отрывное обтекание тел [179], возникновение и развитие циркуляционного течения около тела [143], возникновение и развитие разрушающихся ударных волн на свободной поверхности [154],  обтекание интерцепторов [180],  исследование прорыва воздуха к телам и крыльям [178], гидроупругие колебания кавитирующих и некавитирующих крыльев [176].

Значение полученных результатов состоит не только в обнаружении и  изучении нового неизвестного ранее класса резонансных процессов и вихре-волновых структур, но также и в том, что разработанная концепция вихревых ударных волн и классификация волновых движений и вихревых, грибовидных и древовидных структур позволяет предсказывать и обнаруживать неизвестные ранее формы вихре - волнового взаимодействия, создавать искусственно условия для возникновения этого явления применительно к практическим задачам, а также создавать новые способы и разрабатывать новые конструкции , часть из которых используется в настоящее время в судостроении [180, 192, 193,, 207-209], которые могут найти применение также в других областях техники и научных исследований.

    Широкое поле деятельности открывается также для изучения физических явлений и вихре -волновых структур, которые могут сформироваться при взаимодействии резонансного потока с другими типами волновых и колебательных движений: колебания крыла, качка судна, вибрация, излучение и т.д.

В последнее время предриняты попытки обнаружения подобных явлений в биологии и науках о человеке.

 Авторы высказали гипотезу о том, что подобные явления должны быть широко распространены в биологических и социальных процессах. В частности, вихре - волновой  и структурный резонансы могли играть существенную роль в возникновении жизни. Эта гипотеза требует детальной теоретической  проработки и может явиться основанием для создания нового направления в изучении этой важнейшей научной проблемы.

 Остановимся вкратце на возможности применения этой концепции при экономических исследованиях. Роль неоднородной среды в этом случае играет совокупность объектов и субъектов, между которыми осуществляются производственные и экономические отношения. Так как в экономике уже выработался параметр целого – деньги, то их объём, выраженный в некотором эквиваленте может считаться своеобразным геометрическим размером субъектов экономики. Количество денег, принадлежащих тому или иному субъекту или той или иной корпорации может считаться её размером или длиной эквивалентной ей волны. В экономике постоянно происходит оборот денежной массы. Период полного обращения денежной массы того или иного субъекта экономики может считаться частотой эквивалентной волны. А её скоростью можно считать отношение денежной массы к периоду обращения.

Вся совокупность субъектов экономики обладает неким свойством , которое можно считать эквивалентным дисперсионному соотношению сплошной среды. Каждому субъекту экономической деятельности успешному в данном поле соответствует определённая связь между его объёмом и частотой оборота средств. Эта связь может быть экспериментально определена. Если появляется какой-либо новый участник экономической структуры, то можно предположить, что его деятельность будет успешной, если его капитал  и предполагаемая частота его оборота будут соответствовать дисперсиноому соотношению экономической среды, в которой он собирается действовать. В противном, нерезонансном случае он будет иметь неприятности. Однако указанное условие должно явиться необходимым, но не достаточным условием успеха.

Концепция вихре-волнового и структурного резонанса может быть после соответствующей проверки использована и при выборе партнёров в экономической деятельности. Для  выполнения условий структурного резонанса необходимо, чтобы партнёры имели близкие величины капитала и скорости его оборота. Если же взаимодействуют компании с различными объёмами капитала, то в более крупной компании должно быть подразделение, близкое по объёму к меньшей из компаний.

 

Литература.

 

1. Сунгуров А. Ю. Резонансные взаимодействия в природе.- Синергетика и методы науки. Труды семинара. Под ред. М. А. Басина. СПб.: Наука. С. 431-433.

2. Баранцев Р. Г. Целостность общения.- XIV Международная конференция серии: «Нелинейный мир». Языки науки. Пущино. 3-7 июня 2006. Сборник тезисов. Под редакцией Г. Ю. Ризниченко. С. 18.

3. Басов Н. В. Риск - рефлексия и социальная самоорганизация» - XIV Медународная конференция серии:  «Нелинейный мир». Языки науки. Пущино. 3-7 июня 2006. Сборник тезисов. Под редакцией Г. Ю. Ризниченко. С. 19.

4. Басина Г. И., Басин М. А. Синергетика. Основы методологии. – СПб.: Норма. 2006.-56с. 

5. Басин М. А., Шилович И. И. Синергетика и Internet. Путь к Synergonet. СПб.: Наука. 1999. 72 с.

6. Басин М. А., Шилович И. И. Путь в Synergonet. СПб.: Норма. 2004. 128с.

7.Журавлёва З.Е. И услышал я иной голос. М.: Прогресс – Традиция, 1998. С.127. 193с.

8.Хакен Г.Синергетика. М.: Мир. 1980. 414с.

9. Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. Ижевск: Ижевская республиканская типография. 2000.400 с.

10. Ланда П. С. Нелинейные колебания и волны. М.: Наука. Физматгиз. 1997. 469 с.

11. Мандельштам Л. И. Лекции по колебаниям. Собр. трудов. Том 4. М.: Изд-во АН СССР. 1955.

12. Басин А. М. Качка корабля. М.: Транспорт. 1969. 272 с.

13. Арнольд В. И. Математические основы классической механики. М.: Наука. 1974. 432 c.

14. Якубович В. А., Старжинский В. М. Параметрический резонанс в линейных системах.- М.: Наука. Гл. ред. физ.-мат. литературы. 1987. 328с.

15. Челомей В. Н. Парадоксы в механике, вызываемые вибрациями.- В. Н. Челомей. Избранные труды. М.: Машиностроение 1989. С. 23-28. Материалы данной работы были доложены на заседании Отделения механики и процессов управления АН СССР 7. XII. 1982г., посвящённом 60-летию образования СССР, а также заседании Президиума АН СССР 27. I. 1983г.

16. . Андронов А. А., Витт А. А., Хайкин С.Э. Теория колебаний. Москва. Гостехиздат.1937; Физматгиз. 1959. Наука. 1981.

17. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука. 1984.

18. Ланда П. С., Дубошинский Я. Б. Автоколебательные системы с высокочастотными источниками энергии. – УФН. 1989. Т.158. В.4. С. 729-742.

19. Ланда П. С. Преобразование высокочастотных электрических колебаний в низкочастотные механические. Машиноведение 1988 №6. С. 90-95.

20. Ланда П. С. Электромеханические преобразователи автоколебательного типа. Вибротехника. 1991. №66.С.201-209.

22.                       Шарковский А.Н. Сосуществование циклов непрерывного преобразования прямой в себя  Укр. Матем. Журнал. 1964 Т.26.№1 Сс.61-71.

22. Feigebaum M.J. Quantitative universality for a class of nonlinear transformations.J. Stat. Phys. 1978. V.19.№1. P. 25-52.

23. Feigebaum M. J. The onset spectrum of turbulence Phys. Let.1979 v/74A №6 Pp375-378

24.Nauenberg M.Rudnik J. Universality and the power spectrum at the onset of Chaos. Phys. Rev.B. 1981.V 24B№1Pp493-495

25. Kaneko K. Oscillations and doubling of torus  Progr.Theor.Phys.Japan. 1984.V.72№2 Pp. 202-215

26.Неймарк Ю.И. , Ланда П.С. Стохастические и хаотические колебания. Москва.Наука 1987

27. Анищенко В. С. Сложные колебания в простых системах. М.: Наука 1990.

28. Ruelle D., Takens F. On the nature of turbulence Comm. Math.Phys. 1971.V.20№2Pp.167-192.

29. Vavriv D. M, Ryabov V. R., Sharapov S.A., Ito H. M.Chaotic states of weakly and strongly nonlinear oscillators with quasiperiodic excitation. Phys. Rev. E. 1996 V.53.№1Pp.103-114

30. Милнор. Дж. Голоморфная динамика. Ижевск: НИЦ «Регулярная и хаотическая динамика». 2000. 320с.

31. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Ч.2.СПб.: Норма. 2002. 144с.

32. Басин М. А. Внутреннее и внешнее время в динамике систем. Материалы Международной междисциплинарной научной конференции : «Синергетика в естественных науках» (Третьи Курдюмовские чтения). 19-22 апреля 2007 г. Ответственные за выпуск : Г.П. Лапина, Ю.В. Козловская. Тверь: Твер.глс.ун-т. 2007. С.147-151

33. Bhatnagar P. I. Nonlinear Waves in One-dimensional Dispersive Systems. Claderon Press.Oxford. 1979.  Имеется русский перевод. Бхатнагар П. Нелинейные волны в одномерных дисперсных системах. М.: «Мир». 1983 136 с.

34. Лайтхилл Дж. Волны в жидкости. М.: Мир. 1981. 600 с.

35. Grawford F.S.Waves. Berkeley Physics Course,Volume 3, Mc-Graw-Hill Book Company 1967

36. Feynman R.P., Leighton R.B. , Sands H., The Feynman Lectures on Physics, V.3, Addison-Wesley Publishing Company , INC, Reading,

Massachusetts, Palo Alto, London, 1963.

37. Нелинейные волны. Самоорганизация. Ред.А. В. Гапонов - Грехов, М. И. Рабинович. М.: 1983. 264c.

38. Басин М. А., Завадовский Н.Ю. Модель двойного спирального вихря как предельная форма свободной поверхности для нестационарного потока идеальной несжимаемой жидкости. Труды семинара по обратным краевым задачам . Выпуск 22. Казань: КГУ. 1985.

39. Basin M. A. Wave Formation by the Motion of Surface Ship Hydrodynamic Complex near the Free Boundary. Classification of Nonlinear Waves. Vortex-wave Resonance. Papers of IMAM 93 Congress. Edited by P. A. Bogdanov. Vol. II. Varna . Bulgaria. November 15-20. 1993. P. 51-58.

40. Басин М. А. Волновой подход к исследованию структур и систем . Реальность и субъект. Т.2. № № 2 - 3 СПб.: 1998. С. 57-72.

41. Басин М. А. Основы классификации нелинейных волновых движений, вихрей и транспортных систем. Синергетика и методы науки. (Под редакцией М. А. Басина) СПб.: Наука. 1998. С. 95-131.

42. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Ч. 1. СПб.: Норма. 2000. 168с

43. Басин М. А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно-информационные системы.- Международная междисциплинарная научно-практическая конференция: «Современные проблемы науки и образования». Керчь, 27.06-4.07. 2001. Ч. 1. Харьков. 2001. С. 12-13.

44. Басин М. А. Информационно-волновая теория структур и систем.- Материалы Второй научной конференции Санкт-Петербургского союза учёных: «Проблемы и перспективы междисциплинарных фундаментальных исследований. 10-12 апреля 20 02 года СПб. 2002. С. 8 -9.

45. Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. СПб.: Норма. 2003. 260c.

46. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб.: Норма. 2006. 56с.

47. Васильев В. А., Романовский Ю.М. Яхно В.Г. Автоволновые процессы.- Под ред. Д. С. Чернавского М.: Наука Гл. ред. физ.- мат лит. 1987 – (Соврем. пробл. физики) 240 с.  

48. Режимы с обострением. Эволюция идеи. Законы коэволюции сложных структур. М.: Наука. 1998. 255с. (Кибернетика: неограниченные возможности и возможные ограничения).

49. Реньи А. Трилогия о математике. М.: Мир. 1980. 376с.

50.Hadamard J. Lecons sur le propogation des ondes. Paris: Hermann.1903

51. Kotschin N. E. , Uber starke Diskontinuitaten in einer kompressiblen Flussigkeit", Proceedings of the International Congress for Applied Mechanics. Delft.1925. P.405 - 418.

52. Truesdell A. First Course in Rational Continuum Mechanics. The Johne Hopkins University. Baltimore. Mariland. 1972.

53.Russell J. S. Report on Waves. British Association Reports. 1844.

54. Scott-Russell J. Report on Waves. Proc. Roy. Soc. Edinb., P. 319 – 320.

55. Korteweg D. J., De Vries G. On the Change of Form of Long Waves Advancing in a Rectangular Canal and on a New Type of Long Stationary Waves. London, Dublin and Edinburg Phil .Mag.Ser.5. 39/. 1895. P.422.

56. Zabusky N. J., Kruskal M. D. Interaction of Solitons in a Collisionless Plasma and the Recurrence of Initial States.-Phys. Rev. Lett. V.15. 1965. P.240-243.

57.Березин Ю. А., Карпман В. Л. О нелинейной эволюции возмущений в плазме и других дисперсионных средах. ЖЭТФ.Т.51. 1966. С. 1557 - 1564,

58. Miura R. M., Gardner C. S., Kruscal M. D. Korteweg – de Vries Equation  and Generalization. II. Existence of Conservation Laws and Constants of the Motion.-J. Math. Phys. V. 9. 1966. P.1204-1209.

59. Taniuti T. , Wei C.C. Reductive Perturbation Method in Nonlinear Wave Propagation I., J. Phys. Soc. Japan.V.24. 1968. P. 941 - 966.

60. Кадомцев Б. Б., Карпман В.И., Нелинейные волны. УФН. 103. 1971. С.193-213..

61.Захаров В. Е. ,Фаддеев Л. Д.,Уравнение Кортевега-де-Фриза- полностью интегрируемая Гамильтонова система .-" Функциональный анализ" 1971 Т.5. N 4. С.18-27.

62.Новиков С. П. Периодическая задача для уравнения Кортевега-де- Фриза, "Функциональный анализ "1974.Т.4. N.3. С. 54-66.

63.Newell A.C., Solitons in Mathematics and Physics - University of

64. Тахтаджян Л. А., Фаддеев Л. Д. Гамильтонов  подход к теории солитонов. М.: Наука. 1986. 528 С.

65.Сретенский Л. Н. Теория волновых движений жидкости. М.: Наука. 1977 816с.

66. Stoker J.J. Water Waves .The Mathematical Theory with Applications. Interscience Publishers ,Inc., New York , Interscience Publishers Ltd., London,1957

67. Маклаков Д. В. Нелинейные задачи гидродинамики потенциальных течений с неизвестными границами. М.: «Янус-К». 1997.  280с.

68.Арнольд. В. И. Особенности каустик и волновых фронтов.М.: Фазис 1996. 334 с.

69. Tulin M.P. Supercavitating Flows. Small Perturbation Theory, Journal of Ship Research,1964 v.7 N3.

70.Birkhoff G., Zarantonello E.H., Jets, Wakes and Cavities , New York, 1957.

71.Гуревич М.И.Теория струй идеальной жидкости. Второе издание

М.:"Наука"1979 536стр

72. Егоров И.Т. , Садовников Ю.М, Исаев И.И., Басин М.А. Искусственная кавитация. Л.: Судостроение 1971

73. Варченко А.Н., Этингоф П.И. Почему граница круглой капли превращается в инверсионный образ эллипса.М.: Наука. Физматгиз. 1995. 80с.

74. Управление риском. Риск. Устойчивое развитие. Синергетика.

М.: «Наука» 2000. 431с. (Серия «Кибернетика: неограниченные возможности и возможные ограничения»).

75. Хэссард Б., Казаринов Н., Вэн И. Теория и приложения бифуркации рождения  цикла. М.: Мир. 1985. 280 с.

 76. Басин М. А. Об одной аналогии между одномерными динамическими системами и плоскими гидродинамическ.ими течениями идеальной жидкости.   

77. Pullin D. The Large Scale Structure of Unsteady Self-similar Rolled up Vortex Sheets // Journal of Fluid Mechanics , Vol. 88, N 3 1978

78.Van Dyke M. An Album of Fluid Motion . The Parabolic Press. Stanford,  California.1982

79. Бэтчелор Дж. Введение в динамику жидкости. М.: Мир. 1973. 760с.

80. Басин А.М., Миниович И.Я. Теория и расчёт гребных винтов. Л.: Судпромгиз. 1963. 760с.

81. Вилля Г. Теория вихрей.Л.-М.:ОНТИ-НКТП.1936.266с

82. Миндлин И.М. Интегро-дифференциальные уравнения в динамике тяжёлой слоистой жидкости. М.: Наука. Физматлит. 1996. 304с.

83. Phillips O. M. Wave Interaction . Idea Evolution Journal of Fluid Mechanics . A Special Issue Celebrating the 25th Anniversary of the Journal and Containing Editorial Reflections on the Development of Fluid Mechanics. Volume106, May1981 Cambridge University Press Cambridge-London-New York-New Rochelle - Melbourne -Sydney.

84.         Басин М. А. Вихре - волновой резонанс в гидродинамике подводного крыла. Международный симпозиум по гидродинамике судна , посвященный 85-летию со дня рождения А.М.Басина. Л.:-1995.  С. 399-407.

85.         Лорьер Ж.-Л. Системы искусственного интеллекта. М .”Мир” 1991  

86.         Кузнецов Г. И. , Москалюк С.С., Смирнов Ю.Ф. , Шелест В.П. Графическая теория представлений ортогональных и унитарных групп и ее физические приложения . Киев “Наукова Думка “ 1992 288 стр

87.         Клименко А. В. Основы естественного интеллекта. Ростов на Дону . Издательство Ростовского университета. 1994. 304с

88.         Новое в синергетике .Загадки мира неравновесных структур М.”Наука” 1996“264 с

89.         Басин М.А. Орлов С.Г. Теоретическое исследование свободной транспортной динамической системы. Труды Семинара “ Синергетика и методы науки “ (в печати )

90. Крылов Ю. К. Интаэрология и синергетика. - Синергетика и методы науки. (Под ред. М. А. Басина). СПб.: Наука. 1998. С. 77-94.

91. Крылов Ю. К. Интаэрология: принципы построения целостных систем.- Ценологические исследования. Вып. 3 М.: 1997. Становление философии технетики: техническая реальность и технетика. М.: 1997.

92. Крылов Ю. К., Кудрин Б. И. Целочисленное аппроксимирование ранговых распределений и идентификация техноценозов. - Цитологические исследования. Одиннадцатый выпуск. Москва: Центр системных исследований. 1999. 80с.

93. Басин М. А. К теории идеального трансформера. – Синергетика и методы науки. (Ред. М. А. Басин). СПб.: Наука. 1998. С. 356-375

94.Бутусов К.П. Золотое сечение в Солнечной системе. АН СССР Астрометрия и небесная механика. Серия: «Проблемы исследования Вселенной.» Вып. 7, Москва-Ленинград 1978 С.475-500.

95.Сороко Э.М. Структурная гармония систем. Минск: 1984

96.Смирнов В.Л, Проблемы логики при моделировании самоорганизующихся структур. Синергетика и методы науки (Под редакцией М.А. Басина) – СПб.: Наука. 1998. С. 40-63.

97.Смирнов В.Л. Солнечный цикл: механизм формирования структуры и начальные этапы эволюции. С.390-410

98. Быстров М.В. О шуме 1/f c точки зрения всеобщей гармонии. Синергетика и методы науки (Под редакцией М.А. Басина) – СПб.: Наука. 1998. С. 375-390.

99. Иванов- Ростовцев А.Г., Колотило Л. Г., Тарасюк Ю.Ф. Шерстянкин П.П. Самоорганизация и саморегуляция природных систем. Модель, метод и основы теории D-Self (Под ред. К.Я. Кондратьева. СПб.: Русское географическое общество. 2001. 216с.

100.Буданов В. Г. Ритмокаскады и их роль в космоземных связях.- Стратегия жизни в условиях планетарного экологического кризиса.Т.1.СПб. 2002.С.207-218.

101. Смирнов В.Л. Формирование комплекса узлов на основе протоструктуры. Материалы Международной междисциплинарной научной конференции : «Синергетика в естественных науках» (Третьи Курдюмовские чтения). 19-22 апреля 2007 г. Ответственные за выпуск : Г.П. Лапина, Ю.В. Козловская. Тверь: Твер.гос.ун-т. 2007. С.133-138.ь

102. Буданов В.Г. Методология синергетики в постнеклассической науке и образовании. М.: Издательство ьЛКИ. 2007. 232с.

103. Басина Г.И. , Басин М.А. Сиььььььььььььнергетика. Основы методологии.СПб.: Норма. 2006.

104. Маслов В.П, Квантовая экономика. М.:Наука.2005.

105 .Филиппс О.М. Взаимодействие волн - эволюция идеи. В монографии: “Современная гидродинамика , успехи и проблемы .Редакторы Дж. Бетчелор, Г. Моффат М.: Мир.1984.С. 297-314.

106 .      Michell J. H. The Wave Resistance of a Ship. Philosophical Magazine Ser 5, 1898, Vol. 45. №  272.

107. Havelok  T.H. The Resistance of a Ship among Waves -PRSL. Ser. A 1937. Vol. 161. № 906.

108. Кочин Н.Е. О волновом сопротивлении и подъемной силе погруженных в жидкость тел. Труды конференции по теории волнового сопротивления. М.: Изд. ЦАГИ. 1937.С.1-30.

109.                  Костюков А. А. Теория корабельных волн и волнового сопротивления. Л.: Судпромгиз. 1959.

110 . Басин А.М., Анфимов В.Н. Гидродинамика судна. Л.: “Речной транспорт”. 1961.

111  Справочник по теории корабля. В трех томах. Под редакцией Я. И. Войткунского. Л.: «Судостроение» 1985. 

112 . Келдыш М. В., Лаврентьев М. А. О движении крыла под поверхностью тяжелой жидкости  – Труды конференции по теории волнового сопротивления 1937. М.: Изд. ЦАГИ С. 31-32

113  Седов Л. И. Плоская задача о глиссировании по поверхности тяжелой жидкости. Труды конференции по теории волнового сопротивления. 1937. М.: Изд. ЦАГИ С. 7-30.

114  Владимиров А. Н. Подъемная сила подводного крыла вблизи свободной поверхности. Л.: “Судостроение“. №6. 1937. 

115 .      Чудинов С. Н.  О подъемной силе подводного крыла конечного размаха. Труды ВНИТОСС. 1965. Т.6. Вып. 2 . Сс. 74-92.

116                     Блюмин В. И., Иванов Л. А., Масеев М. Б. Транспортные суда на подводных крыльях. М.: Транспорт. 1964.

117                      Егоров И. Т., Соколов В.Т. Гидродинамика быстроходных судов. Л.:”Судостроение”1971, 424с.

118                      Эпштейн Л. А. Методы теории размерностей и подобия в задачах гидромеханики судов . Л.”Судостроение”. 1970

119                      Федоров Е. А. Плоская задача о движении тела произвольной формы под свободной поверхностью идеальной невесомой жидкости. Труды НТО СП. 1968 . Вып. 104. С. 126-133.

120                     Логвинович Г. В. Гидродинамика течений со свободными границами Киев.: “Наукова думка”. 1969. 216 с.  

121 . Басин М. А. Шадрин В. П. Гидро- аэродинамика крыла вблизи границы раздела сред . Л.:  Судостроение. 1980. 304с.

122 . Панченков А.Н. Исследование движения подводного крыла вблизи свободной поверхности жидкости. Автореферат диссертации. Киев 1962

123 . Nishiyama T. Lifting line theory of the submerged hydrofoil of finite span”, Parts 1,2,3. Journal of the American Society of Naval Engineers. 1959-1960. Vol. 71-72

124 .      Isai W.H. Zur Theorie der nahe der Wasseroberflache fahrenden Tragflacher . Ing Arch 27(1959/60) S.295

125                     Панченков А. Н. Гидродинамика подводного крыла. Киев.: «Наукова думка» 1965. 552 с.

126  Salvesen N.(1981) “Five Years of Numerical Naval Ship Hydrodynamics at DINSPDC” // J. Of Ship Research.  Vol.25. № 4 Pp. 219-235     

127        Басин М.А. О силах, действующих на крыло, движущееся вблизи свободной поверхности весомой жидкости. Доклад на конференции: “ Гидродинамика крыла , движущегося вблизи свободной поверхности жидкости , и глиссирующих поверхностей». Л.:1982.

128        Ткач А. Я. О влиянии весомости среды на гидродинамические характеристики несущей поверхности . Доклад на конференции: ”Гидродинамика подводного крыла . движущегося вблизи свободной поверхности  жидкости и глиссирующих поверхностей.“ Л.:. 1982.

129 .      Макасеев М. А. К решению плоской задачи обтекания тонкого гибкого профиля под поверхностью тяжелой жидкости . Доклад на конференции Гидродинамика подводного крыла . движущегося вблизи свободной поверхности  жидкости и глиссирующих поверхностей.“1982. Л.:.

130 .      Лотфуллин М.В. Движение системы профилей под свободной поверхностью весомой жидкости . Доклад на конференции: «Гидродинамика подводного крыла . движущегося вблизи свободной поверхности жидкости и глиссирующих поверхностей.» Л.: 1982.

131  Лордкипанидзе А.Н. Расчет гидродинамических характеристик тонкого крыла большого удлинения и сопоставление результатов расчета с экспериментальными данными. Доклад на конференции «Гидродинамика подводного крыла . движущегося вблизи свободной поверхности  жидкости и глиссирующих поверхностей.»Л.:1982.

132                     Ткач А. Я. О влиянии весомости среды на гидродинамические характеристики несущей поверхности Проблемы гидродинамики судна. Труды ЛКИ .Л.Изд-во ЛКИ. .1983. С.76-82.

133                     Басин М. А., Лордкипанидзе А.Н., Ткач А. Я.  Явление вихре-волнового резонанса при исследовании гидродинамических характеристик подводного крыла, движущегося вблизи свободной поверхности весомой жидкости . Труды НТО СП . Вып. 414, Л.:”Судостроение”1985. Стр.23-31.

134                      Басин М.А., Лордкипанидзе А.Н., Ткач А.Я. Решение задачи о стационарном движении несущей поверхности вблизи границы раздела сред. Вихре-волновой резонанс. Труды НТО СП. Вып.1. Л.: 1990.C.115-127

135.       Корнейчук А. А. Квадратурные формулы для сингулярных интегралов . Численные методв решения дифференциальных и интегральных уравнений и квадратурные формулы. 1964 т.4 №4 Сс.64-74.

136                      Мишкевич В.Г. О построении квадратурных формул для сингулярных интегралов , встречающихся в гидроаэродинамике . Вопросы судостроения . Серия : “ Проектирование судов “ 1980. Вып. 23 С. 98-108

137                      Гребные винты . современные методы расчета ( Бавин В. Ф.,Завадовский Н.Ю., Левковский Ю.Л. , Мишкевич В.Г)., Л.: “ Судостроение “1983. 236 с.

138                     Лотфуллин М.В. Филиппов С.И. Обтекание профиля весомой жидкостью вблизи границ раздела сред. Механика машиностроения . Тезисы докладов II республиканской научно-технической конференции . Секция механики жидкости, газа  и плазмы . Брежнев. 1987. С. 44.

139                     Щигунов В.Г. Решение нелинейных нестационарных волновых задач вихревым методом. Канд. диссертация . СПб.: СПбГМТУ.

140                      Duncan G. G. An Experimental Investigation of Breaking Waves Produced by a Towed Hydrofoil //Proc.R. Soc.London.1981. Vol.A377.

141                      Basin M.A. A Wave Formation by the Motion of Surface Ship Hydrodynamic Complex near the Free Boundary. Classification of Nonlinear Waves. Wave-vortex Resonance.// Papers of IMAM 93 Congress/ Ed. by P.A. Bogdanov. Vol.II. Varna. Bulgaria. November 15-20.1993. Pp.51-58.

142                      Басин М.А. Основы классификации нелинейных волновых движений , вихрей и транспортных систем //Синергетика и методы науки. Под. ред. М.А.Басина. СПб. «Наука» 1998. Сс.95-131.

143                     Басин М. А.,, Шапошников И.Г. Новая модель нестационарного течения около крыла в невязкой жидкости. Математическое и физическое моделирование в гидродинамике судна . Труды НТО СП . Выпуск 18. Л.: Судостроение .1989. С.27-38.

144                     Lanchester F. W. Stability of an Aerodrome. Доклад на собрании Бирмингемского общества. 19 июля 1884.

145. Lanchester F. W. Aerodynamics. London 1907

146. Аэродинамика . Под общей редакцией Р.Ф. Дюренд. Том I. ОНТИ НКТП СССР . 1937. 436 с.

147..Жуковский Н. Е О наивыгоднейшем угле наклона аэропланов. Воздухоплавание и исследование атмосферы. Вып.1. 1897

148. Kutta W. M. Auftriebskrafte in stromenden Flussigkeiten. Illustrierte aerodinamische Mitteilungen.  1902. S.133.

149. Жуковский Н.Е. О присоединенных вихрях . Сообщена автором в Московском математическом обществе 15 ноября 1905 и напечатана в трудах отделения физических наук ОЛЕ  т. XIII. Вып.2 1906.

150. Чаплыгин С.А. О давлении плоско-параллельного потока на преграждающие тела . Московский математический сборник №28 . 1910.

151. Longue -Higgins M. S., Fox M. J.H.  Theory of the almost -highest Wave . The Inner Solution . -Journal of Fluid Mechanics. 1977 V.80 . Pр.721-742.

152. Юэн Г. Лэйк Б. Нелинейная динамика гравитационных волн на глубокой воде. Механика. Новое в зарубежной науке. №.41. М.: Мир. 1987. 184 с.

153 Нелинейные волновые процессы . Механика. Новое в зарубежной науке №.42 . М.: Мир. 1987. 296 с.

154 Амромин Э.Л., Басин М.А. Бушковский В.А. Два решения пространственной задачи о предельных волнах на поверхности весомой жидкости. Прикладная математика и механика т.54. N1. 1990.

155. Xu H., Yue D.K. P. Numerical Study of Three-dimensional Overturning Water Waves// Proc/ of 7th Int. Workshop on Water Waves and Floating Bodies. 1992. Pp.213-216.

156.                  Маклаков Д.В. Нелинейные задачи гидродинамики потенциальных течений с неизвестными границами. М.: «Янус-К». 1997. 280 с.

157. Басин М.А. Об изменении вектора суммарной завихренности сплошной среды при движении в ней твердого тела и при движении ее внутри твердого сосуда. ИАН СССР. Механика жидкости и газа №1 М.: 1984.

158. Басин М.А. Изменение моментов поля завихренности жидкости при движении в ней твердого тела// Совершенствование ходовых , мореходных и маневренных качеств судов. Материалы по обмену опытом. Вып. 400. Л.: ”Судостроение”. 1984. С.49-54

159. Басин М.А. Основные уравнения вихревого движения жидкости. Вихре-волновой резонанс. Материалы по обмену опытом. Труды НТО СП. Л:.Судостроение. 1990.

160. Basin M.A. Вasic Equations of Vortex Fluid Motion. Vortex-Wave Resonance. IUTAM Symposium on Separated Flows and Jets. Novosibirsk: USSR 1990. Pp.39-41 Springer - Verlag. Berlin -Heidelberg 1990. V. V. Kozlov , A.V. Dulov (Editors).Pp.113-116.

161 Basin M. A. Basic Equations of Vortex Fluid Motion. Selected Papers.Vol.1. Applied Hydrodynamics. St-Petersburg. State Marine Technical University. 1993. Pp. 23-34.

162. Басин М.А., Корнев Н.В., Захаров А.Б. Аппроксимация трехмерных вихревых полей. Труды Центрального научно-исследовательского института морского флота. СПб.:1993. 184-196.  

163. Басин М.А., Корнев Н.В. Аппpоксимация поля завихpенности в неогpаниченной сpеде. ЖТФ РАН, Ноябpь, 1994, CПб. Сс. 179-185

164. Basin M.A., Kornev N.V. New Computational Method of Vortex Dynamics. Report on the Euromech Colloquium 315. Nurnberg Erlangen. Germany. March.1994.

165. Basin M.A., Kornev N.V.Approximation of Vorticity Field in an Unbounded Volume. Tech. Phys. 39 (11) 1994, American Institute of Physics. Pp.1184-1187

166.  Basin M.A., Kornev N.V. Vortex Methods in Hydrodynamics. International Symposium on Ship Hydrodynamics Devoted to 85-th Anniversary of Birthday of Abram M. Basin (ISSH).St-Petersburg, May, 1995, pp.431-450

167 . Basin M.A., Kornev N.V. Berucksichtigung der Reibung in der Wirbelmethode. ZAMM.78 №5 1998.Ss.29-52.

168. Basin M.A.Kornev N.V.  A Way to Split the Navier-Stokes Equations in the Context of Vortex Method. “ Communications in Numerical Methods in Engineering “

169 Басин М.А., Лордкипанидзе А.Н., Ткач А.Я. Гидродинамические характеристики несущего комплекса, движущегося вблизи свободной поверхности весомой жидкости. Труды Семинара по краевым задачам. Выпуск 26 Аэродинамика течений с неизвестными границами Казань: КГУ 1991.Сс.29-59

170. Basin M.A., Lordkipanidze A. N., Tkach A. Ja. Vortex-Wave Resonance in the Hydrodynamics of Foil, Moving near the Interface of the Different Density Media // Waves and Vortices in the Ocean and their Laboratory Analogues. The Fifth Annual Workshop of the Commission on the Problems of the World Ocean. Vladivostok, September  23-29. 1991. Pp.15-16.

171.Басин М.А. Основы классификации нелинейных волновых движений и вихревых структур. Явление вихре-волнового резонанса при движении несимметричных тел в неоднородной жидкости// Проблемы гидромеханики в освоении океана Материалы конференции по прикладной гидромеханике Киев ИГМ АНУ 1992 Сс.192-193

172  Basin M.A. Wave Formation by the Motion of a Surface Ship Hydrodynamic Complex near the Free Boundary . Classification of Nonlinear Waves. Wave-Vortex Resonance. Proceedings of the VI Congress of the IMAM. Edited by Peter A. Bogdanov . Volume II, 15-20 November 1993. Varna. Bulgaria

173. Basin M. A. Vortex-wave Resonance in Hydrofoil Hydrodynamics. International Symposium on Ship Hydrodynamics Devoted to 85-th Anniversary of Birthday of Abram M. Basin(ISSH). St-Petersburg: May, 1995, pp.399-407.(0.6)

 174. Басин М.А. Вихре-волновой резонанс// Синергетика и методы науки. Труды семинара. . Oтветственный редактор M.А. Басин. С.-Пб.“Наука” 1998 .c.415-418.

175.  Егоров И. Т. , Садовников Ю.М. ,Исаев И. И. Басин М. А. Искусственная кавитация , Л. “Судостроение”1971. 284 с.

176. Басин М.А. Лабок Л.Ю. Шалларь А.В. О связи режима обтекания и гадроупругих колебаний крыльевых систем быстроходных судов. НТО СП. Материалы по обмену опытом. Вып. 186 Л:”Судостроение”.1972 Сс.76-87.:

177. Егоров И.Т., Басин М.А., Садовников Ю.М., Шалларь А.В. Методика экспериментального исследования нестационарных гидродинамических характеристик кавитирующих подводных крыльев. НТО Судпрома. Экспериментальная гидродинамика судна.  Материалы по обмену опытом Вып.190. Л.: ”Судостроение”, 1972.  Сс94-100 

178 Basin M.A., Shaposhnikov, I. G., Zilist L. P. Problems , Methods and Results in Hydrofoil Cavitation// Proceedings of the Second International Symposium on Cavitation . April 1994 Tokyo, Japan pp.99-105

179. Basin M.A., Borisov R.V., Greengoltz A.I., Guseev A.S. Kagan I.S Theoretical and Experimental Determination of the Forces of Viscous Nature by the Vibration of the Bodies at the Fluid. Proceedings of  XV Ubileum Seminar on the Ship Hydrodynamics. Varna: Bulgaria. 1986

180.  Басин М. А., Бочагов В. И., Мизина М. Я., Охрименко Г. Г., Пономарев А. В., Сидоров В.П. , Титов В. Г. Результаты теоретико -экспериментальных исследований несущих поверхностей с интерцeпторами . Доклад на Всесоюзном семинаре по отрывным течениям. Новосибирск 1988.

181.   Князева Е.Н. Курдюмов С.П. Законы эволюции и самоорганизации сложных сиситем. М.: Наука. 1994. 238 с.

182.    Синергетика и методы науки (Ред. Басин М.А.) СПб.: Наука 1998. 440 с.

183. Баранцев Р.Г. Синергетика в современном естествознании. М.: 2003.

184. Данилов Ю. А. Причудливый ми науки. Саратов.Изд.Гос. УНЦ «Колледж» .2004.

185.       Иванов А. Н. Теоретическое исследование гидродинамических характеристик крыльевых профилей при кавитации. Материалы IX научно-технической конференции по теории корабля. Л.:”Судостроение 1968

186.       Иванов А.Н. Кавитационное обтекание профилей крыльев . ИАН СССР . Серия механики и машиностроения 1960 Вып.6 С.117-119 .

187.       Tulin M. P. Supercavitating Flow  pst Foils and Struts . Symposium on Cavitation in Hydrodynamics . London 1956

188.       Tulin M. P. Supercavitating Flows . Small Perturbation Theory .  J.S.R.1967 , Vol 7. №3.

189.       Guerst J. A. Linearized Theory for Partially Cavitating Hydrofoil . International Shipbuilding Progress 1959 Vol 6. № 60

190.       Wade R.B. Linearized Theory for Partially Cavitating Plane -Conveх Hydrofoil Including the Effects of Comber and Thickness. J. R. 1967 Vol. 11 №1.

191.       Терентьев А.Г. Плоские стационарные задачи теории струйных и каитационных течений . Автореферат докторской диссертации . Казань КГУ 1972.

192.       Косов Б.В. , Шалларь А. В. Гидродинамические характеристики профилей крыльев в переходном режиме кавитационного обтекания . Материалы по обмену опытом . Труды НТО СП .Экспериментальная гидродинамика судна.Вып.226. .Л.”Судостроение“

193.       Басин М.А., Шалларь А.В. Нестационарная схема обтекания кавитирующего крыла установившимся потоком.  Труды НТО СП. Вып.192 .Л.”Судостроение“ 1973

194        Кнэпп.Р. Дейли Дж.,Хэммит Ф. Кавитация . М.: “Мир” 1974.

195.       Ильин В. П. Структура и шумообразование при пленочной кавитации. Всесоюзный симпозиум по проблемам кавитации. Одесса .1971.

196.       Левковский Ю.Л. Структура кавитационных течений . Л.: Судостроение. 1978 224 cтр.

197.       Walchner O. Profilmessungen bei Kavitation-Hydromechanische Probleme des Schiffsantriebs. Hamburg 1932

198.       Numachi F. Kraftmessungen an fier Flugel -profilen bei Hohlsog Forschung auf dem Gebiete des Ingeneur wesens. Band 11, №6, 1940.

199.       Иванов А.Н. Гидродинамика развитых кавитационных течений. Л.”Судостроение”1980 240 с.

200.       Meijer M.C. Some Experiments of partly Cavitating Hydrofoils . International Schipbuilding Progress Vol 6. №60 Аugust 1958 .

201.       Биркгоф Г. Сарантонелло Э.Струи, следы и каверны. М.: “Мир “1964.

202        Чжен П. Отрывные течения М.: Мир 1972-1973. Тт.1-3.

203.       Гогиш Л.В. , Нейланд В.Я. , степанов Г.Ю. Теория двумерных отрывных течений . Гидромеханика (Итоги науки ) 1975.тт7.8

204. Нейланд В.Я. , Степанов Г.Ю. Ламинарные и турбылентные течения . В кн.:” Современные проблемы теоретической и прикладной механики .” Киев : “Наукова думка”1978.С.216-232

205.       Гогиш Л.В. , Степанов Г.Ю. Турбулентные отрывные течения М.:”Наука“1979,367с

206. Хёрмандер Л. Анализ линейных дифференцальных операторов с частными производными. В четырёх томах. М.:Мир.1986.

207.       Басин М.А., Косов Б.В. Шалларь А. В. Способ уменьшения сопротивления и вибрации крыльевого гидродинамического профиля .АС №477 879 от 29.03.75. Заявка №1938937 с приоритетом от 2.07.73

208.       Басин М.А. , Косов Б.В. ,Шалларь А.В. Крыло с системой управления кавитацией , А.С. № 524729 от 22.04.76. Заявка №2023987 с приоритетом от 12.05.74.

209.       Косов Б.В. , Шалларь А.В. Крыльевое устройство судна на подводных крыльях .А.С. №1080348 от 15.11.83 Заявка №3505758 с приоритетом от 08.07.82. 

210. Фрост Р. Ручей, текущий к западу. Из девяти книг.(Перевод А.Сергеева. М.:ИЛ.1963

211. Карман Т. Сверхзвуковая аэродинамика. Принципы и приложения. М. Государственное издательство иностранной литературы. 1948. 100с.

212. Франкль Ф.И. Карпович Е.А. Газодинамика тонких тел. М.-Л.: ОГИЗ - Гостехиздат. 1948.  176с.

213. Рахматуллин Х. А., Сагомонян А. Я., Бунимович А. И., Зверев И. Н. Газовая динамика. М.: Высшая школа. 1965. 724 с.

214. Ван Дайк М. Альбом течений жидкости и газа.М.: Мир. 1986. 184с.

215. Басин А.М., Веледицкий И.О., Ляховицкий А. Г. Гидродинамика судов на мелководье. Л.: Судостроение. 19

216. Басин А. М. Судно наименьшего волнового сопротивления на мелководье.Труды ЛКИ. 1940 Вып.V.

217. Басин А. М. Исследование движения судна в канале. Труды ЦНИИРФ, 1956. Вып.XXIII.

218. Басин А. М. Приближёное исследование волнового сопротивления судна, движущегося со сверхкритическими скоростями. Труды ЦНИИРФ, Л.: 1959. Вып.XXXIX.

219. Басин А. М. О форме судна наименьшего сопротивления , движущегося со сверхкритическими скоростями. Труды ЛИВТ. 1962 Вып. 33.

220. Басин А. М. Тонкие суда наименьшего сопротивления , движущиеся со сверхкритическими скоростями. Труды ЛИВТ. 1974. Вып. 147.

221. Басин А. М., Веледницкий И. О., Ляховицкий А. Г., Степанюк Е. И. Сверхкритические режимы движения судов на мелководье.  Сборник «Сопротивление воды движению судов», Материалы по обмену опытом. НТО СП им акад. А.Н. Крылова. Л.: «Судостроение» 1969. Вып.127. 

222. Басин А.М. Ляховицкий А.Г. Со сверхкритической скоростью «Водный транспорт» 1969. № 135 (5574)

223. Басин А.М., Ляховицкий А. Г. Особенности гидродинамики мелкосидящих судов со сверхкритическими скоростями. «Речной транспорт» 1972. № 12.

224. Басин А.М., Ляховицкий А. Г. Перспективы развития быстроходных водоизмещающих судов. «Речной транспорт» 1972. № 6.

 225. Басин А.М., Ляховицкий А. Г. Речные водоизмещающие суда со сверхкритическими скоростями. «Судостроение» 1972. № 7.

226. Веледницкий И.О., Ляховицкий А.Г. Влияние характеристик теоретического чертежа на остаточное сопротивление быстроходных водоизмещающих судов в условиях мелководья. Труды ЛИВТ. 1968.

227. Веледницкий И.О., Ляховицкий А.Г., Степанюк Е.И. Некоторые вопросы ходкости и мореходности судов со сверхкритическими скоростями хода. Теория корабля. Материалы к XXIII научно-технической конференции ЛИВТ . 1969.

228 Ляховицкий А. Г. Сравнительная оценка сопротивления воды движению однокорпусных и двухкорпусных судов со сверхкритическими скоростями. Труды ЛИВТ. 1972. Вып. 133.

229.Basin M.A. The Influence of Froude Number Calculated by Displacement on the Form of the Hydrodynamic Complex of Surface Ships. II Symposium on High Speed Marine Vehicles. Naples Castel dell’Ovo 25-26 March 1993/

230.Basin M.A., Lordkipanidze A,N., Mizina M. Ja., Zelensky B.M., Waldman V. A. Computer Technology for Design of Hydrodynamic Complex of Dynamically Supported  Crafts. Proceedings of the VI  Congress of the IMAM. Edited by Peter A. Bogdanov, Vol III. 15-20 Nnovember 1993. Varna. Bulgaria. P.289-296

231. Basin M. A., Ljakhovitsky A. G., Shur S.B., Zelensky  B.M. The Methods of Determining of Fast Catamarans Hydrodynamic Complex  Characteristics. IMAM Proceedings of the VII Congress. Edited by Vladimir Androchec and Josip Lovri

232. Basin M. A., Ljakhovitsky A. G., Shur S.B., Zelensky B. M. Hydrodynamics of Fast Catamarns. Proceedings of Fast 95. Berlin-Hamburg. August-September 1995. P.57-67.

233. Шмидт – Ниельсен К. Размеры животных. Почему они так важны? М.: Мир.1987 .

 

 

 

 

          

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                                Этюд 25

 

                             

Ода границам

 

.

Граница - это нечто, отделяющее одну среду от другой.

Обычно это узкая зона резкого изменения параметров среды.

Если соседствуют две среды с различными физическими свойствами, то граница между ними - это область, в которой происходит быстрый переход от свойств a одной среды к свойствам другой. Во многих случаях этот переход можно считать скачкообразным. При таком предположении граница раздела трёхмерных сред может рассматриваться как двумерная поверхность. Если граничат три среды с различными свойствами, то их общая граница может считаться одномерной линией. В случае, если соседствуют четыре различные среды, то их граница может считаться «физической точкой». Поэтому для оп/исания и классификации границ, в частности, может быть использована геометрическая теория поверхностей и линий.

Мы познаём мир через границы, отделяющие одну структуру от

другой.  Границы являются для нас основным источником информации об окружающих  предметах. Отсюда вытекает неразрывная связь между понятиями граница и информация.  Второй закон термодинамики утверждает, что все явления в природе приводят к росту энтропии, к размыванию границ, увеличению однородности. Но границы возникают и возникают вновь.  Можно предположить, что явление формирования и роста границ определяет некоторые не сформулированные до настоящего времени законы, действующие  в сторону, противоположную действию второго закона термодинамики.

Можно мыслить себе как минимум два механизма формирования новых границ.

Первый механизм - превращение локальных микроскопических дислокаций за счёт потери устойчивости в макроскопические структуры. При этом площадь границы может расти  экспоненциально или взрывным образом. Так формируются трещины в твёрдых телах, паровые пузырьки в кипящей воде или при кавитации. При этом образуется новая среда, информацию о которой мы получаем через образовавшуюся границу. Однако, этот механизм не может считаться основным. Ведь для его реализации  необходимо предположить существование микроскопической дислокации. А последняя каким-то образом должна быть создана. Тем самым,  проблема происхождения границ сводится к проблеме происхождения дислокаций, которая сама по себе не проще.

Существует ещё один механизм формирования границ, который, как нам кажется, лишён этого недостатка, - формирование ударных волн в сплошной среде. Этот механизм привлекает к себе ещё тем, что для его описания может быть использован строгий и изящный математический аппарат. Не зря именно его Я. Б. Зельдович принял в качестве гипотезы об основном механизме формировании структуры Вселенной («блины» Зельдовича), тогда как возникновение самой Вселенной, по-видимому, происходило в соответствии с первым механизмом.

 Механизм формирования ударных волн объединяет в единое целое, казалось бы,  не связанные между собой классы структур: линейные и нелинейные волны в сплошной среде и границы раздела сред.

Последнее обстоятельство позволило нам объединить границы раздела фаз и классические ударные волны в один класс нелинейных ударных волн. Сюда же мы отнесли солитоны и волновые режимы с обострением, открытые С. П. Курдюмовым и его коллегами. В этот класс может быть включена гипотетическая суперударная волна, теоретически исследованная нами в настоящем сборнике как комплексная модификация фундаментального решения уравнения теплопроводности

Так как границы являются для нас основными источниками информации об окружающем  мире, то на основе анализа их свойств можно попытаться построить оригинальную теорию информации. Предпосылки к такой теории мы попытаемся изложить ниже. Вопрос о соотношении такой гипотетической теории с классической теорией информации требует специального рассмотрения.

Количество информации, отбираемой макроскопической двумерной границей нулевой толщины из микромира, можно считать пропорциональным площади двумерной границы и скачку того или иного параметра на ней. Если  принять этот подход, то увеличение площади двумерной границы, на которой осуществляется скачок параметров среды, должен приводить к увеличению в макромире объёма информации о микромасштабе структуры, которую она ограничивает. Информация, отбираемая средами из микромира, локально оказывается качественно большей на границе раздела трёх сред. И, наконец, наибольшая неоднородность, а следовательно, наибольшее локальное извлечение макроскопической информации из микромира происходит в «физической точке» пересечения границ четырёх сред. В таких «точках» должен наиболее ярко проявляться творческий потенциал природы.

Нами высказана гипотеза о том, что в таких макроскопических «точках» происходит сочетание того, что кажется несочетаемым.  Особая точка сохраняется, меняя своё положение в пространстве, а, возможно, и состав микрочастиц, её формирующих. Тем самым она приобретает  волновые свойства. Не исключено, что именно в этих «точках» создаются условия, при которых появляются принципиально новые структуры - возможно появление жизни.

Границы  имеют различные свойства в зависимости от типа сред, которые они разделяют.

Остановимся первоначально на границах твёрдых тел. При малых скоростях и нагрузках можно считать твёрдые тела абсолютно жёсткими.  В системе координат, связанной с движущимся телом, граница неподвижна и её перемещение в абсолютной системе координат однозначно определяет перемещение  движущегося  тела.  Граница  несёт полную и даже избыточную информацию о  характере перемещения абсолютно твёрдых тел.

Если рассматривать движение твёрдого тела более детально, то необходимо учитывать упругость среды и деформации, максимальная величина которых опять - таки чаще всего возникает на границах . Если нагрузки на движущееся твёрдое тело достигают критической величины, то создаются условия для разрушения твёрдого тела. Либо возникает текучесть, либо в районе дислокаций начинают развиваться трещины. И в том и в другом случае происходит  увеличение площади двумерной границы, а, следовательно,  информации, отбираемой из микромира. Окончательным результатом такого процесса является перезамыкание границы, приводящее к размножению структур. Происходит изменение типа информации. Вместо одного твёрдого тела появляются два или более. Однако при этом дальнейший отбор информации из микромира прекращается.

Появление трещин сопровождается ещё одним явлением: нарушением аналитичности границы. Возникает линия излома границы,  которая в свою очередь, в дальнейшем,  приводит к новым особенностям при взаимодействии сред.

По- иному ведут себя границы между жидкими и газообразными средами.

Во - первых, они становятся деформируемыми, по ним могут перемещаться волны, например, гравитационные волны на поверхности воды. Рост амплитуды гравитационных волн  приводит к появлению завихрённости  и изломам на поверхности раздела сред , а затем к множественным  перезамыканиям  с последующим брызгообразованием.

Во - вторых, на этих границах возникают диссипирующие вихревые пограничные слои, трансформация которых приводит к превращению границ в новые вихревые и грибовидные структуры.

Рассмотрим первоначально более простой случай движения твёрдого тела в идеальной несжимаемой жидкости или газе. Ввиду различия физических свойств твёрдого тела и жидкости (или газа) на границе раздела возникает тонкий  слой разрыва скоростей, интенсивность которого растёт с ростом относительной скорости движения. При наличии на границе тела изломов интенсивность порожденного движением скачка скорости в жидкости или газе теоретически может стремиться к бесконечности. При этом локально на границе происходит дополнительный отбор информации из микромира, интенсивность которого в угловых точках может достигать значительных величин. В жидкости (или газе) возникает в макромире пограничный слой со скачком касательных скоростей. Возникают условия для обратного отбора энергии и информации из макромира в микромир. Вихревой слой  диффундирует внутрь жидкости или газа и, практически сохраняя свою интенсивность, размазывается по нормали к границе. Скачок скорости исчезает. Уменьшается макроскопическая информация о явлениях микромира. Растёт энтропия макроскопического потока.

Из наших рассуждений вытекает вывод о том, что, если мы каким - либо образом увеличим извилистость  границы, сохраняя её толщину, то тем самым увеличим количество информации, отбираемой из микромира. Идеальным вариантом может стать среда с фрактальной тонкой границей, по которой, как по лифту, информация перетекает   из микромира в макромир. Однако здесь необходимо учитывать другое явление,  действующее в противоположную сторону, - явление перезамыкания границы. Перезамыкание двумерной границы предельно малой толщины приводит к слиянию различных участков границы - уменьшению  её площади. А следовательно, к уменьшению макроскопической информации. Одновременно на слившихся частях границы может возникнуть свободный вихревой слой - граница принимает новые свойства.

Эти два процесса могут происходить с различной интенсивностью, и окончательный результат может соответствовать как к росту информации о микромире, так и её уменьшению. Этими процессами можно управлять. Тем самым среды с близкими к фрактальным границами должны обладать специфическими информационными свойствами.

Наши рассуждения могут иметь отношение к анализу такого сложного явления как турбулентность, возникающего, в частности, в недрах ламинарного пограничного слоя. При увеличении относительной скорости движения жидкости и твердого тела внутри пограничного слоя образуется тонкий подслой, неустойчивый к малым возмущениям. В пограничном слое развиваются волны . Возникает новый механизм отбора информации из микромира. Возникшие волны достигают большой высоты и опрокидываются, одновременно теряя продольную устойчивость. При  этом возникают многочисленные перезамыкания, которые вновь уменьшают информацию в макромире о микроскопических явлениях.  В результате, при неуправляемой турбулентности, по-видимому, количество информации уходящей из макромира превышает количество извлечённой из микромира. О том, что этим соотношением можно управлять, говорит высокая эффективность применения полимерных добавок.

При движении твёрдых тел в сжимаемой жидкости или газе дополнительным источником информации о микромире являются формируемые звуковые волны, порождающие неоднородность макроскопической плотности. Наиболее характерно это проявляется при возникновении звуковых ударных волн, представляющих резонансные скачки плотности, перемещающиеся со скоростью звука. Здесь также происходит обратный процесс диффузии ударной волны, сопровождающийся потерей макроскопической информации.

До последнего времени загадочными казались процессы, связанные с так называемым отрывом пограничного слоя, имеющие прямое отношение к рассматриваемой проблеме. Как удалось показать М. А. Басину и Н. Ю. Завадовскому, здесь главную роль играет специфическая  вихревая ударная волна, возникающая в пограничном слое при наличии положительного  градиента давлений.  Эта вихревая ударная волна может реализоваться в виде двойного спирального вихря, внутри которого вновь могут происходить множественные перезамыкания, приводящие к существенной потере макроскопической информации. Из двойного спирального вихря формируется вихревой пузырь, имеющий свою внешнюю границу.  Граница некоторой структуры при помощи обнаруженного механизма вихревых ударных волн сама превращается в новую структуру – вихревой пузырь.

Существует непосредственная и многосторонняя связь между угловыми точками на твёрдой границе и вихревыми пузырями, которая может быть названа обобщённым постулатом Чаплыгина – Жуковского - Кутта, состоящая в том, что в угловых точках  устойчиво течение, при котором скачок скорости минимален.

Рассмотрим качественно механизм реализации этого постулата  для двух наиболее интересных и практически важных случаев, в результате которых деформации границы формируют две различные модификации грибовидных структур.

Первый вариант описывает формирование циркуляции и подъёмной силы  на крыле. На границе движущегося тела имеется как минимум две критические точки, то есть точки, в которых скорость жидкости или газа в завихрённой области близка к скорости движения тела и наблюдаются максимальные продольные градиенты завихрённости.  Если здесь провести вполне уместную аналогию с фазовым пространством конечномерной динамической системы, то критические точки около движущегося крыла окажутся во многом аналогичными седловым точкам сепаратрисы фазового пространства. И так же, как вблизи седловых точек фазового пространства конечномерной динамической системы возможно появление бифуркации рождения цикла, впервые обнаруженной А. А. Андроновым, вблизи критических точек  потока может сформироваться вихревой пузырь. Это тем более вероятно, чем ближе критическая точка к острой задней кромке крыла. Взаимодействуя с потоком около крыла, вихревой пузырь сходит с поверхности, меняя циркуляцию вокруг профиля крыла. Этот процесс происходит до тех пор, пока градиент скорости на острой задней кромке не станет минимальным.

При этом вблизи концевых кромок крыла конечного размаха образовавшаяся вихревая пелена – вихревая ударная волна второго рода окаймляется постоянно формирующимися вихревыми пузырями. Возникает одна из форм пространственной дипольной структуры, которую мы назвали грибовидной.  Возникшая структура достаточно сложна, так как содержит растущую во времени вихревую пелену, окаймлённую полузамкнутым вихревым пузырём, замыкающимся вихревым пограничным слоем на поверхности крыла. При этом на крыле возникает циркуляция и значительная поперечная сила. Возникновение грибовидной структуры этого типа, сопровождающееся появлением циркуляции на крыле и значительными поперечными силами, что широко использовано в многочисленных технических приложениях. Не меньший объём приложений осуществлён в динамике живых организмов. Элементы получившейся грибовидной структуры движутся с существенно    различными скоростями и вследствие этого её продольный размер растёт во времени. Это позволяет изучать отдельные элементы независимо  друг от друга, что и делается при использовании соответствующих гидродинамических моделей теории крыла. Формирование кормового вихревого пузыря является резонансным процессом. Его размеры и интенсивность его циркуляции резонансно определяются формой и углом атаки крыла. Без этого ограничения процесс формирования вихревого пузыря мог бы продолжаться неограниченно. Механизм схода кормового вихревого пузыря с  задней кромки крыла во многом аналогичен излучению фотона. Возможно, что его подробное изучение прольёт свет на природу постоянной тонкой структуры.

Мгновенно изменив угол атаки симметричного относительно продольной оси крыла до нуля, можно получить замкнутый вихревой пузырь с перемычкой в виде вихревой пелены, который можно считать определенным типом свободной грибовидной структуры. В случае, если продольный размер полученной грибовидной структуры уменьшается,  всё более проявляется её дипольный характер.

Второй пример постулата Чаплыгина-Жуковского- Кутта соответствует формированию струи, вытекающей из круглого отверстия. В данном случае граница круглого отверстия представляет собой совокупность угловых точек, вблизи которых формируется кольцевой вихревой пузырь, который при определённом соотношении между его размерами и радиусом отверстия отрывает себя от стенки, оставляя за собой вихревую струю. Формируется грибовидная структура другого типа, которая во многом напоминает биологические грибовидные структуры.

Грибовидные структуры в жидких и газообразных средах появляются на границах турбулентного пограничного слоя, при обтекании плохообтекаемых тел, при атомном взрыве и в ряде других случаев. Уравнения, описывающие динамику этих процессов, известны. Механизм формирования грибовидных структур в этом частном случае может быть изучен досконально, и  результаты могут быть использованы при исследовании более общего класса структур, которые также могут быть названы грибовидными. Такие структуры широко представлены в различных явлениях природы, главным образом, в биологических и социальных .

Анализ свойств гидродинамических грибовидных структур позволяет выделить как минимум три типа связанных нелинейных волновых процессов, в которых участвует грибовидная структура.

1. Перемещение границы структуры относительно окружающей среды - грибовидная структура как тело – волна.

2. Обмен структуры со средой материальными и информационными ресурсами.

3. Циркуляция материи, энергии и информации внутри грибовидной структуры.

Участие в этих процессах может служить определением принадлежности исследуемой структуры к классу обобщённых грибовидных структур. К этому классу относятся, в частности, Вселенная, галактики, звёзды, планеты, Земля, океаны, материки, атмосфера, облака, биологические клетки, живые организмы, биоценозы, Биосфера, Человеческое  общество, многие технологические и социальные структуры, создаваемые Человеком.

Грибовидные структуры вследствие своей сложности могут участвовать в различных бифуркационных событиях и процессах, в частности, в процессах полного или частичного размножения и слияния, в результате которых появляются новые грибовидные структуры различной степени сложности. Одновременно размножаются отдельные волновые элементы, входящие в грибовидные структуры. Таким образом, вблизи границ раздела сред формируются новые транспортно - информационные системы, которые в свою очередь одновременно обладают всеми свойствами грибовидных структур. Для  их упрощенного исследования возможно использовать, в частности, математические методы теории графов и сетей.

Необходимо обратить внимание на существенную роль границ при реализации открытого нами явления вихре - волнового и (или)  структурного резонанса. Сущность этого явления состоит в аномальном взаимодействии границ сред и грибовидных структур между собой и с диспергирующими волнами при определённых резонансных соотношениях геометрических и кинематических параметров.

Одним из основных параметров, определяющих  динамику живых и неживых объектов является время. При этом практически все объекты имеют начало и конец во времени, то есть границы не только в пространстве, но и во времени. Моменты возникновения и  исчезновения  структуры характеризуют временные границы процессов.

Изложим предполагаемый нами сценарий возникновения жизни, отметив, какую роль в этом процессе играют   границы.

Это происходило несколько миллиардов лет тому назад на побережье океана или какого-либо иного водоёма.  Граница пересечения трёх стихий: воды, воздуха и земли - постоянно меняющая своё положение - береговая линия являлась очень активной зоной с меняющимся материальным составом.  Земную поверхность можно считать, пронизанной микроскопическими порами, которые то покрывались жидкостью, то выходили на воздух.  Энергия, необходимая для активности этой  зоны, имела, как минимум, два источника: солнечное излучение, энергия вулканического происхождения.

Когда волны набегали на берег, вода выходила из пор, образуя грибовидную структуру, которая  отрывалась от своей базы, образуя нечто подобное коацерватным    каплям Опарина. В случае ухода воды жидкость  входила в поры, как в дырку от ванной, закручиваясь при этом. В этой зоне скапливались и взаимодействовали различные элементы, образуя внутри пор закрученные спирали. Так как эти процессы происходили периодически, граница оказывалась заполненной грибовидными структурами с закрученными ножками, которые, захватываются шляпками грибов, образуя первичные ДНК. Так формировались праклеткп, которые состояли из тех же элементов, что и окружающая  активная среда, но специфически организованных. Многие из них разрушались, но некоторые, наиболее приспособленные, росли в объёме и размножались, поглощая из окружающей среды нужные им вещества и структуры.

Механизм такого поглощения необходимых веществ и структур и последующего выбрасывания продуктов обмена может быть качественно в духе Синергетики описан на примере простых , но достаточно общих моделей. В рамках такого описания наиболее ярко проявляется роль границ.

Пусть мы имеем два тела - волны, ограниченные замкнутыми двумерными деформируемыми  границами, схематизирующие шляпки грибовидных структур. С целью простоты рассмотрения будем пренебрегать всеми видами взаимодействия, кроме тактильного. Пока границы не касаются, тела перемещаются в пространстве независимо друг от друга. С момента касания границ начинается их непосредственного взаимодействие. В первый момент взаимодействие происходит в одной  точке. Затем совместная площадь взаимодействия границ начинает расти, образуя зону двойной границы. Здесь мы принимаем часто оправдывающуюся гипотезу непротекания границ. Тем самым общая часть границ двух тел приобретает одну общую нормальную скорость и скачок касательных скоростей – становится вихревой поверхностью. Может возникнуть также  скачок и других параметров границы.  Определёнными особенностями обладает меняющаяся во времени одномерная граница зоны смыкания границ двух взаимодействующих тел. Нормальная к ней поверхность сечения содержит в первое время раздваивающуюся линию, для геометрии которой может быть получено аналитическое  выражение. Здесь могут быть рассмотрены два предельных случая.  Первый состоит  в том, что обе старые границы подходят к новой по одной общей касательной, которая одновременно является касательной к общей части границ пересекающихся тел.

Второй случай соответствует тому, что общая касательная двум старым границам нормальна к нормали к новой. Первый вариант должен наблюдаться в начальный период взаимодействия – второй - позднее. Переход от первого ко второму должен происходить нетривиально и требует специального изучения. Во втором случае рост общей границы может прекратиться и вместо двух структур формируется одна комбинированная, граница которой состоит из двух бывших ранее независимыми частей. Общая часть оказывается внутри и играет роль переборки. Этот процесс может быть почти обратимым - удар упругого мячика об пол ,- а может быть и необратимым –склеивание двух предметов.  В случае необратимого процесса образовавшаяся внутренняя переборка может рассосаться , а может потерять устойчивость и фрактализоваться.

Перезамыкание границы одного тела - волны может привести к противоположному результату – появлению двух тел-волн или множественному образованию тел – волн. То есть качественному изменению информационных характеристик изучаемых структур.

Эти два «элементарных» события могут комбинироваться различным образом , формируя широкое множество бифуркационных событий, которые интегрально приводят как к увеличению , так и уменьшению информации об изучаемой системе.

Рассмотрим кратко два специальных варианта, имеющие, на наш взгляд, наиболее важное значение. Первый вариант – это поглощение одной структурой другой, начинающееся таким же образом, как и в первом основном варианте, но оканчивающееся тем, что граница одной структуры поглощает  границу другой. Таким образом, граница одного тела оказывается внутри границы другого. Дальнейшее поведение внутренней границы  неоднозначно. Она может рассосаться и тогда  происходит полное уничтожение одного из тел. Она может сохраниться и тогда поглощаемое тело  образует ядро внутри поглощающего.

Второй вариант более сложный: частичное поглощение одной структурой другой с одновременным разделением поглощаемой структуры.

Если поглощения одной структурой других полезных для её существования структур при одновременном выбрасывании вредных происходит регулярно, то мы получаем волну обмена структуры с окружающим полем. Здесь можно ввести простую количественную математику для изучения структуры как волны, а следовательно применить при исследовании взаимодействия структур концепцию структурного резонанса.

Качественно новые представления о формировании и роли границ, однако базирующиеся на выше изложенных соображениях, возникают при исследовании биологических систем и, тем более, при изучении человеческого общества. При этом специальное внимание необходимо уделить проблеме «цвишенизма», подробно рассмотренной , в частности, в работах Р. Г. Баранцева.

 

 

                                             

 

 

 

 

                                                          

 

 

 

 

 

                                                          Этюд 26

 

                                                    Границы и жизнь

 

 

 

В монографиях [1-8] нами изложены результаты теоретических и экспериментальных исследований,  позволившие сформулировать две новые концепции:

концепцию масштабного резонанса;

концепцию вихре - волнового и (или) структурного резонанса.

Использование этих концепций позволило создать принципиально новую классификацию волн, вихрей, грибовидных и древовидных структур и транспортно - информационных систем, а также  теоретически предсказать существование резонансных аномальных явлений при движении структур и систем в неоднородной сплошной среде, которые затем были обнаружены экспериментально.

Резонансные процессы, являющиеся комбинациями масштабных и структурных резонансов, наиболее часто встречаются в биологических и социальных системах.

 Наиболее ярким примером применимости концепции вихре – волнового и (или) структурного резонанса может стать проблема возникновения живого.

Изложим некоторые гипотезы.

Важную роль в решении этой проблемы играют резонансные нелинейные процессы формирования и деформации границ. Двумерные границы рассматриваются в нашей классификации как одна из форм нелинейных ударных волн, образование которых приводит к появлению в сплошной среде зон скачкообразной неоднородности, а, следовательно, к уменьшению энтропии и появлению новой макроскопической информации.

 В динамике резонансных грибовидных и древовидных структур, а также транспортно-информационных систем, к которым относятся все живые организмы,  границы несут главную  информационную нагрузку, передавая информацию из микромира в макромир. Живые организмы устроены таким образом, что формирующие их структуры и системы имеют максимально возможную площадь границ различных масштабов.

Еще большую информацию о микромире в макромир передаёт линия, представляющая собой пересечение двух границ.

Но максимальная информационная нагрузка возникает в точке, в которой пересекаются три границы.

Существуют ли такие области в Природе?

 Да. Если мы рассмотрим четыре стихии Аристотеля:

земля,

вода,

воздух

и огонь,-

то пересечение границ между ними должно привести к появлению малой особой области, в которой формируются структуры, элементы которых обладают максимальной неоднородностью.

 Именно в таких  особых точках согласно нашей гипотезе должна была зародиться и   развиваться   жизнь

            Побережье Мирового Океана и побережья локальных водных пространств могут рассматриваться как линии пересечения двух границ. Если в этой области локально добавить «огонь» в виде Солнечного света или вулканических извержений (проблема «чёрных курильщиков»), то реально создаются условия для возникновения и длительного существования разнообразных резонансных форм устойчивых в своей неустойчивости вихревых и грибовидных структур, которые можно отождествить с одной из форм живых организмов.  

Эта гипотеза требует детальной проработки и может явиться основанием для формирования нового направления в изучении важнейшей научной проблемы возникновения жизни. Если она подтвердится, то подобный механизм может быть использован для создания принципиально новых нано   – технологий, имеющих дело с объектами, лежащими на границе живого и неживого.

 

                           Литература

 

1. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168 с.

2. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144 с.

3. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71 с.

4. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.

5. Басина Г. И., Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с.

6. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.

7. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с.

8. Басина Г. И., Басин М. А. Синергетика. От чисел Басина до Synergonet. Этюды. Internet. Сайт С. П. Курдюмова.

 

 

 

 

 

                                                     Этюд 27

К теории творческого потенциала

 

 

Есть только миг между прошлым и будущим

Именно он называется жизнь.

 

 

Одной из вечных загадок природы является время – параметр, который определяет всё наше существование, течение которого происходит, казалось бы, независимо от нас. При этом нам кажется, что мы можем измерять поток времени и даже управлять его течением.

Характерным свойством времени является его необратимость. В реальной жизни мы не можем вернуться в прошлое. Это можно сделать лишь мысленно, в нашей памяти. Существует реально лишь один момент времени – настоящее, в который мы осуществляем некоторые действия. Всё, что было до этого, уже прошло и оставило свои следы в нашей памяти, в нашем нынешнем состоянии, в окружающей нас природе. Всё, что будет, является для нас не вполне определённым, то есть таким, что не может быть нами однозначно предсказано и обязательно достигнуто. Будущее не является фатальным, а хотя бы частично зависит от наших желаний и нашей воли. Это свойство может быть названо необратимостью времени. В отличие от пространства, в каждое место которого мы, в принципе, можем вернуться, вернуться в прошлое, насколько нам известно, не удавалось никому. При математическом описании  процессов окружающего мира время является основным параметром, характеризующим динамику изменения состояний различных структур и систем. При этом  выделяются два типа процессов.

    Процессы, практически обратимые во времени, будущее  поведение структур и систем в которых, в принципе, может быть предсказано однозначно. Такие идеальные процессы описываются при их моделировании, например, законами Ньютона для консервативных систем или обобщающими их уравнениями Шредингера для квантовой физики. Фактически для таких процессов время в нашем обыденном понимании вообще не течёт. Оно как бы исчезает, становится мнимым. Модели таких процессов описывают большое количество явлений окружающего мира. Утверждалось, что они всеобщи, во всяком случае, для неживой природы.  

    Это утверждение противоречит необратимому характеру процессов, происходящих с живыми организмами, в частности, с каждым из нас. Однако и сама необратимость процессов также двояка. Процессы с течением времени могут деградировать, а могут развиваться, творя все большее количество структур и систем. При этом законы деградации и законы творения существенно отличаются друг от друга.

    Особое внимание следует обратить также на характер нашего восприятия настоящего, прошедшего и будущего времени. Мы можем ощущать только настоящий момент времени, тот, в который мы существуем. Этот момент как бы скользит с определенной скоростью по шкале времени, совпадая с моментами, которые были для нас будущими, и затем оставляя их в прошлом, к которому мы можем  вернуться только в своей памяти. Это ещё одно проявление необратимости  и творческого характера времени. Прошлое как бы выталкивает нас в настоящее, а затем и в будущее, творит новые объекты и события.

    Закономерности протекания тех или иных процессов во времени и в пространстве мы можем выразить математически с помощью изучения уравнений движения и их решений. Так, например, обратимые процессы выражаются математически в виде решений обыкновенных дифференциальных уравнений для положения структуры в пространстве или волновых уравнений для некоторых функций и потенциалов.

    Однако существуют дифференциальные уравнения в частных производных, некоторые решения которых принципиально несимметрично зависят от времени. Это параболические уравнения, простейшим линейным частным случаем которых является одномерное уравнение теплопроводности:

.                                         (1)

    Мы считаем, что подробный анализ его фундаментального решения может пролить новый свет на природу зависимости процессов окружающего мира от времени. Фундаментальное решение уравнения теплопроводности даётся формулой Пуассона [1] .

 

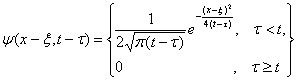  ,                                  (2)

где функция , описывающая процесс, несимметрична относительно момента измерения  (настоящего момента). До этого момента она считается равной нулю. В завершение настоящего момента она представляет собой дельта - функцию Дирака, которая затем диффундирует, сохраняя неизменным и равным  единице интеграл, взятый вдоль оси x.

    Это свойство решения уравнения теплопроводности позволяет интерпретировать его как распределение вероятности реализации того или иного события и считать его описывающим математически деградационные процессы, происходящие в природе. Оно же является символом  второго закона термодинамики – закона роста энтропии. В пределе при очень больших положительных значениях времени фундаментальное решение (2) при всех значениях координаты стремится к нулю, сохраняя интеграл по пространственной координате равным единице. Время при таком подходе выполняет роль меры деградации родившейся ниоткуда в момент  структуры. Следует  обратить внимание на то, что на отрицательной шкале относительного времени  функция , описывающая состояние системы, равна нулю. Система как бы рождается из ничего в момент  и далее начинает деградировать, сохраняя некоторый инвариант. Но рождение из ничего противоречит нашим представлениям о природе. Всё новое рождается из чего-то старого. Таким образом, решение (2) уравнения (1) не является полным.

  Как можно в данном случае найти  старое? Каков механизм творения новых структур, которые появляются «из ничего». Попытаемся ответить на этот вопрос.

     Будем считать, что функция, описывающая процесс, должна быть комплексной и аналитически продолжаться в область отрицательных значений моментов относительного времени. Для этого можно формально подставить в формулу Пуассона (2) отрицательные значения относительного времени .

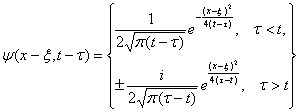 .                                       (3)

 

Формула (3) обладает следующими свойствами.

    Первое свойство состоит в том, что динамическая функция  при отрицательных значениях относительного времени перестаёт быть действительной величиной.  Реальная часть этой функции обращается в нуль, как и в выражении (2).

Во-вторых, появляется мнимая часть, которая может иметь два значения, отличающиеся знаком.

В-третьих, необычным оказывается поведение получившейся функции в зависимости от координаты. Минимальное значение она имеет при =0, то есть в точке, в которой при положительных значениях относительного времени рождается новая реальная структура. С увеличением модуля координаты эта мнимая функция растёт как экспонента квадрата координаты.

В четвёртых, рост модудя этой функции от времени при приближении к моменту  также происходит чрезвычайно быстро, здесь возникает неинтегрируемая особенность.

    В пятых, при всех значениях , приближаясь к моменту «рождения» структуры, мнимая часть функции стремится к бесконечности.

При этом переход через точку = 0 во всех местах, кроме  =0, обращает действительную и мнимую части комплексной характеристической функции в нуль. Создаётся впечатление, что момент = 0 является мощным барьером, около которого концентрируется некий мнимый творческий потенциал, интенсивность которого растёт по мере удаления от точки рождения реальной структуры.

В самом слабом месте, вблизи точки =0 этот потенциал рождает и выталкивает реальную структуру в область реального положительного относительного времени, где она существует, деградируя во времени и диффундируя в пространстве. Если предположить, что ось времени замыкается на бесконечности, то функция, переходя на бесконечности через нуль, возвращается обратно уже в виде пары интенсивно растущих мнимых функций творческого потенциала. Круг замыкается.

    Попытки найти в окружающем нас мире некоторые аналоги подобного поведения реальных структур и систем приводят нас к выводу, что подобное творческое поведение происходит в живой и неживой природе.

Из огромного количества семян, число которых резко возрастает к моменту созревания, рождается одно реально существующее растение, которое затем, погибая, вновь рождает  огромное количество семян. Конечно, жизнь намного сложнее простейшей математической модели, описанной нами выше, однако качественное описание процесса рождения рассмотренная нами модель даёт.

По близкому сценарию происходили, по нашему предположению, три основных творческих    процесса во Вселенной:

-рождение Метагалактики,

-зарождение жизни,

-возникновение человеческой популяции.

Взрыву Метагалактики должен был предшествовать некий творческий потенциал, природу которого следует изучать научными методами.    

    Перед возникновением живого должен  был существовать творческий потенциал в виде многообразия органических молекул.

    Возникновению человеческой популяции предшествовал творческий потенциал многообразия биологических видов.

Любое соревнование, в котором победитель (чемпион) получает всё,  может  быть приближённо описано полученным выше решением (3).

 Подобное творческое поведение наблюдается при теоретическом исследовании зарождения и диффузии вихрей в вязкой жидкости. Вихревые потоки рождаются сингулярно в зонах неоднородностей и на границах жидкости, а затем диффундируют в соответствии с уравнением теплопроводности внутрь жидкости.

    Мнимость характеристической функции при отрицательных значениях относительного времени, возможно, свидетельствует о том, что эта функция характеризует некоторые информационные процессы, а именно творческий потенциал.

В классической триаде Р. Г. Баранцева  [2] она может отвечать за «интуицио». Так, в результате «озарения» после усиленного мысленного напряжения рождается новая идея.

Стремящийся к бесконечности скачок характеристической функции при нулевом значении относительного времени может быть назван комплексной суперударной волной и включён во второй класс нелинейных волн в соответствии с предложенной нами классификацией [9].

 

    В пользу целесообразности выполненного нами анализа и возможности нахождения его реальных аналогов говорит следующее очень важное обстоятельство.

Мы можем наряду с действительным рассматривать и мнимое время. В этом случае уравнение теплопроводности превращается в уравнение Шредингера для свободной частицы, а его решение характеризует волновую функцию сохраняющейся во времени перемещающейся в пространстве свободной элементарной частицы [3]. По утверждению основоположников квантовой механики, это уравнение и его частный случай: уравнение Ньютона, - описывают все инерционные процессы в неживой природе, происходящие со скоростями, намного меньшими, чем скорость света. Если в него добавить ещё один член, отвечающий за потенциальные силы и учесть достижения теории относительности, в которой априори рассматривается мнимое время, то, по их мнению, можно описать все явления неживой природы.

    Но введение мнимого времени является лишь естественным следующим шагом в нашем рассмотрении. То, что рассмотрение мнимого времени  дало  результат, который вместе со своими обобщениями практически описывает большую часть современных физических представлений, говорит о том, что и первый сделанный нами шаг имеет право на включение его в фундамент современной науки.

Следующим шагом должно быть рассмотрение фундаментальных решений уравнений с комплексным временем и комплексными координатами. Некоторые примеры эффективности подобного рассмотрения приведены в [4-10].

    Возражения против выполненного анализа могут быть высказаны в связи с тем, что при стремлении относительного момента времени к нулю со стороны прошлого модуль мнимой части характеристической функции имеет неинтегрируемую особенность. Однако, это может свидетельствовать также о существовании некоторого малого ( и одновременно очень большого обратного ему) параметра, характеризующего неопределённость настоящего момента времени и связанное с этим ограничение величины характеристического потенциала сверху. Этот параметр может быть связанным с постоянной Планка, а может быть и не зависимой от неё константой Природы.

 

Литература.

 

1.   Михлин С. Г. Линейные уравнения в частных производных. Учебное пособие для вузов. М.: Высшая школа».1977. 431 с.

2. Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

3. Каку М. Введение в теорию суперструн. М.: Мир .1999. 634с.

4. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168с.

5. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144с.

6. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71с.

7. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.

8. Басина Г. И.,Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с

9. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма.2006. 56 с.

10. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с

 

 

 

 

 

 

 

 

 

 

Этюд 28.

 

О новом типе крыла с максимальным аэро - гидродинамическим качеством

 

1 января 2011.

 

Авторы благодарят Р. Г. Баранцева предложенное им название для описанной конструкции

 

Аэроколесо

 

    Несущие или управляющие крылья широко используются как в живой природе, так и в различных механизмах и транспортных средствах, создаваемых человеком. При этом их применение оказывается эффективным, если они при заданных размерах создают максимальную подъёмную силу, либо имеют максимальное аэро - гидродинамическое качество, то есть отношение подъёмной силы к сопротивлению.

С целью решения последней задачи крылья стараются проектировать плавно обтекаемыми, чтобы избежать отрыва пограничного слоя и возникновения вихревого сопротивления, связанного с отрывом. При этом максимальным аэро - гидродинамическим качеством обладают крылья, создающие вовсе не максимальную подъёмную силу.

А между тем законы аэро - гидродинамики вовсе не запрещают проектировать крыльевые устройства, обладающие одновременно максимальной подъёмной силой и максимальным гидродинамическим качеством.

В настоящей работе сделана попытка найти принципиально новые пути технического решения поставленной проблемы. Если высказанные качественные теоретические соображения найдут экспериментальное подтверждение, то возникнет возможность создания принципиально новых конструкций в различных областях техники.

Классической задачей гидро - аэродинамики является задача об обтекании идеальной жидкостью круглого цилиндра бесконечного размаха. До сих пор нас удивляет парадокс  Эйлера, основным утверждением которого является равенство нулю сопротивления такого цилиндра (да и не только цилиндра, но любого тела). Однако, в случае цилиндра имеется ещё один парадокс. Сопротивление при двумерном обтекании остаётся нулевым, если на поток вокруг цилиндра наложить произвольную циркуляцию. А циркуляция, в соответствии со знаменитой формулой Н. Е. Жуковского, однозначно определяет подъёмную силу произвольного двумерно обтекаемого контура. Таким образом, для одного и того же цилиндра в идеальной жидкости можно теоретически получить бесконечное гидродинамическое качество при любом значении подъёмной силы крыла. В действительности дело обстоит не так просто. В реальной жидкости вблизи поверхности цилиндра формируется вязкий пограничный слой, и на поверхность тела со стороны жидкости действуют касательные напряжения,  интеграл проекций которых по поверхности тела даёт вязкостное сопротивление трения. Поэтому бесконечного значения аэро - гидродинамического качества добиться практически невозможно.        В случае обтекания кругового цилиндра вследствие большого градиента скоростей на наружной границе пограничного слоя возникает явление, называемое отрывом пограничного слоя, приводящее к возникновению широкого, зачастую нестационарного следа, на формирование которого тратится дополнительная энергия, что приводит к перераспределению давлений по поверхности цилиндра  и возникновению значительного дополнительного сопротивления. Поэтому выводы, полученные на основе теории идеальной жидкости, становятся абсолютно не соответствующими действительности.

 

Но идеал всё же существует и к нему нужно стремиться.

 

 Прежде всего, остановимся на проблеме формирования циркуляции. При решении задач аэро – гидромеханики методами идеальной жидкости циркуляция вводится в поток принудительно, по желанию исследователя. Правда, для относительно тонких крыльев с острой задней кромкой существует постулат Жуковского – Чаплыгина – Кутта, позволяющий однозначно определить циркуляцию потока, исходя из предположения о конечности скорости в районе этой кромки. Справедливость этого постулата,  приблизительно подтверждённая экспериментальными данными, является одной из не решённых до сих пор проблем. Правда, в последнее время нам удалось сделать важный шаг в её решении . Дело в том, что реальные течения районе задней кромки не могут в принципе иметь бесконечных скоростей. Если  где – либо в потоке возникает тенденция к неограниченному росту скорости, а это чаще всего бывает вблизи поверхности крыла, то там же возникает тенденция  к росту градиента скорости, отрыву пограничного слоя и формированию присоединённых к поверхности крыла, а затем отрывающихся в поток концентрированных вихревых образований. Этот  процесс продолжается до тех пор, пока течение не станет таким, что вблизи острой кромки скорость не станет конечной. В этом режиме движение около крыла станет устойчивым. Любое возмущение приводит к появлению вблизи задней кромки концентрированного вихря, сход которого вновь стабилизирует течение таким образом, чтобы выполнялся постулат  Жуковского-Чаплыгина - Кутта. У кругового цилиндра нет острой задней кромки. Наивный способ  придания цилиндру вращения также не годится, так как вращение цилиндра возмущает лишь близлежащие слои жидкости, а для того, чтобы создать реальный циркуляционный поток, необходимы существенные энергетические затраты. Да и механизм формирования циркуляции в жидкости или газе, как мы видели, совсем иной. Поэтому, попытки создания подъёмной силы на обтекаемых жидкостью или газом вращающихся цилиндрах кажутся бесперспективными.

    Но сияющие вершины бесконечного аэро – гидродинамического качества при любом значении циркуляции, а следовательно, и подъёмной силы, манят, вероятно, не нас одних. Наметим вкратце пути,  которые могут привести к этим вершинам.

    Обратим внимание на одну особенность циркуляционного течения около цилиндра  в идеальной жидкости. Для простоты рассмотрим плоскую задачу. На границе обтекаемого жидкостью круга возникают две критические точки, в которых скорость жидкости относительно цилиндра равна нулю. При отсутствии циркуляции эти точки симметрично расположены в носовой и кормовой точках цилиндра. При принудительном введении в поток идеальной жидкости циркуляции носовая и кормовая критические точки перемещаются вниз, если наложение циркуляции вызывает появление подъёмной силы, направленной вверх. При этом скорости на верхней стороне цилиндра увеличиваются, а градиенты скоростей уменьшаются.

    Как же можно в действительности получить такое течение?

    Для этого необходимо конструктивно выполнить два условия.

1.   Обеспечить возникновение критической точки в том месте, на границе кругового контура, которое соответствует заданному значению циркуляции.

2.   Обеспечить безотрывное обтекание засасывающей  стороны цилиндра.

Эти две задачи могут быть одновременно решены.

Первая - путём установки в районе критической точки интерцептора.

Вторая – вращением цилиндра. При этом цилиндр может вращаться не принудительно, а свободно, под воздействием набегающего потока. В идеале должно быть обеспечено безотрывное циркуляционное обтекание цилиндра с большими значениями коэффициента подъёмной силы и высоким значением аэро - гидродинамического качества.

    Если высказанные теоретические соображения найдут экспериментальное подтверждение, то откроется широкое поле деятельности по созданию принципиально новых устройств в различных технологических приложениях.

    Этот результат может оказаться по своему значению эквивалентным изобретению колеса.

P.S. Предлагаемая конструкция использует открытое нами явление вихре-волнового и (или) структурного резонанса (смотри Этюд 26).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9

 

Эттюд 29

 

Вероятностный  анализ бифуркационных событий, в которых участвует система.

 

1.   Определение бифуркационного события и графа структур и событий.

 

Эргодичность, возникающая при теоретическом изучении динамических систем, теоретическое обнаружение и исследование странных аттракторов, а также анализ бифуркаций, происходящих в детерминированных динамических системах в связи с изменениями управляющих параметров свидетельствуют о том, что даже в случае кажущихся нам детерминированными  математических моделей иногда проявляется основное свойство природных процессов – их принципиальная неполная предсказуемость. Даже у специальных детерминированных моделей типа динамических систем это свойство проявляется в случае потери  устойчивости их стационарных состояний или других аттракторов.   Для сложных систем их принципиальная недетерминированность, то есть отсутствие возможности точного предсказания будущего поведения самой системы (волны) и её элементов (квантов) становится  их  основной особенностью. Это свойство определяется тем, что подобные системы, взаимодействуя с окружающим полем, принимают обычно участие в так называемых бифуркационных событиях, которые становятся для них скорее правилом, чем исключением.

 Мир состоит из взаимодействующих между собой волн, структур и систем, которые с той или иной степенью достоверности могут быть выделены из окружающей среды. Всю мировую историю  можно представить себе как эволюцию взаимодействующих структур и систем.

    Простейшей математической моделью эволюции систем является граф, названный нами графом структур и событий, одной из координат которого является время.

    Узел эволюционного графа с малыми отрезками прилегающих к нему ребер (событие) соответствует определенному критическому моменту эволюции.

    Естественная классификация графов и соответствующих им свободных групп может служить основой классификации типов ветвей мировой эволюции [12], [13], в том числе и эволюции человеческого общества.

     Во многих случаях внешнее проявление взаимодействующих структур или систем кажется нам детерминированным, состояния систем до момента взаимодействия полностью определяют их состояния после взаимодействия, то есть после свершения события. Вот что пишет П.Тейяр де Шарден [2 ] «…с качественной точки зрения нет никакого противоречия в том, что мир внешних механизированных видимостей строится из «свободных сущностей» (liberties).3.

Однако, свободные сущности П. Тейяра де Шардена – объекты природы,- иногда  проявляют свою свободу. В этом случае исход события не может быть предсказан однозначно. Поэтому для адекватного отражения реального мира эволюционный граф должен иметь еще одну координату - бифуркационную. Мир устроен таким образом, что предсказать исход того или иного события не всегда представляется возможным.

Пусть имеются две исходные структуры, входящие в нашу систему, которые вступают во взаимодействие. Можем ли мы заранее знать, что произойдет в результате взаимодействия? Будет ли результат однозначным? Вовсе не всегда повторение казалось бы одинаковых опытов приводит к однозначному результату. События, результаты которых не могут быть однозначно предсказаны, будем называть бифуркационными событиями.[16]

Знание о будущем событии – это возможность предсказания времени его свершения и его исхода.

Однако, для бифуркационного события мы не можем однозначно предсказать его исход. В лучшем случае мы можем на основании предыдущего опыта определить множество возможных исходов и вероятность реализации каждого из них. В принципе, это множество может быть как непрерывным, так и дискретным, как одномерным, так и многомерным. В этом случае граф структур и событий приобретает новую обобщённую координату – бифуркационную.

    Здесь уместно ввести аналогию с дорогой, по которой едут автомобили. Дорога может быть одна, дорог может быть много, дороги могут разделяться и сливаться, они образуют некоторый граф или сеть возможных (разрешённых) путей. Каждая развилка дороги – это бифуркационное событие, в результате прохождения которого может быть выбран тот или иной путь следования, возможно, с некоторой вероятностью. Изучаемая нами система взаимодействующих структур – это автомобиль, который едет по дороге, и на каждой развилке (бифуркация - двойная вилка) выбирает тот или иной путь. Каждый индивидуальный автомобиль проезжает только один путь. Проблема взаимодействия индивидуальных автомобилей и сети разрешенных для них дорог есть аналог основной проблемы, связанной с построением бифуркационной проекции графа структур и событий.

    Каждому  бифуркационному событию соответствует не один, а несколько или бесконечное множество результатов, которые могут реализоваться  после свершения события. Эти результаты образуют множество возможных результатов данного события. Если событие произошло, то из всего множества возможных результатов реализуется один, и дальнейшее развитие процесса происходит лишь по одному из возможных сценариев до тех пор, пока не произойдет новое событие с несколькими возможными исходами.

И так далее. Вновь и вновь! Таким образом, формируется новая размерность – бифуркационная размерность. При этом каждый вариант результатов взаимодействия может иметь свое количество результирующих структур.

Зная предшествующее событию состояние системы, время свершения события и возможные его исходы, мы можем построить любое структурно - бифуркационное сечение будущего (сечение по возможным разрешенным дорогам).

    С другой стороны, если взаимодействующие структуры рассматривать как единую динамическую систему, то бифуркационное событие - это такая качественная трансформация параметров системы, которая может вывести на несколько различных аттракторов (зон притяжения).

    Перевязка аттракторной и вероятностной интерпретаций исходов бифуркационного события дала путеводную нить к выяснению механизмов многозначности результатов почти идентичных  событий.

Будущее известно лишь с какой-то вероятностью. При этом изучение законов природы позволяет лишь снизить до минимума  неопределенность в этом знании (уменьшить число допустимых дорог, по которым должна двигаться автомашина).

Однако, будущее может через некоторое время стать настоящим и, если считать, что о настоящем известно все (что в действительности не совсем так, а иногда  совсем не так, и здесь источник еще одной неопределенности, связанной с невозможностью четкого выделения структур),  то принципиально всегда можно уменьшить неизвестность будущего до нуля, сделав его настоящим, после чего оно становится прошлым, и вновь неизвестным, но по-другому.

В графе структур и событий могут быть выделены определенные области (ветви), начинающиеся с какого-либо события и кончающиеся каким-либо событием, которые обладают некоторой независимостью от остальных областей графа. Такие ветви были названы нами процессами [16].

    Если бы все процессы были принципиально различны, то граф структур и событий не мог бы быть изучен. Каждый новый процесс был бы непредсказуем. Да и мы не смогли бы существовать в таком мире. В действительности, всегда среди процессов, входящих в граф структур - событий, имеются процессы, в чем-то аналогичные друг другу.

    Исследование процессов, аналогичных данному, то есть тому, в котором участвует исследуемая нами система, позволяет в случае бифуркционных процессов, определить несколько возможных траекторий развития  и даже, зная частоту встречи той или иной траектории,  приближенно определить вероятность реализации каждой из них.

    Это можно сделать лишь в том случае, если нам удастся включить исследуемую систему в качестве кванта в какую - либо обобщённую волну и исследовать эмпирически динамику поведения некоторого значительного количества аналогичных систем (квантов).

    Каждому варианту возможной фазовой траектории изучаемой динамической системы как модели реального объекта можно сопоставить некоторое число, характеризующее относительную частоту встречи этого варианта траектории в процессе эксперимента, называемое вероятностью реализации.

    Выбор этих чисел производится таким образом, чтобы их сумма по всем вариантам равнялась единице.

Здесь мы можем использовать глубоко развитый аппарат теории вероятностей, основные представления которого применительно к бифуркационному событию с конечным числом возможных исходов мы изложим в настоящем разделе.

 

2.Математика для события с двумя возможными исходами.

 

Как нами будет показано позднее, любое бифуркационное событие при его анализе за счёт факторизации вероятностного пространства или идентификации его исходов может быть на первом этапе рассмотрения сведено к бифуркационному событию с двумя возможными исходами.

Так как последующее рассмотрение является принципиально важным, проведем его достаточно подробно, следуя  в основных идеях [18].

Рассмотрим первоначально простейший вариант, когда в результате события могут возникнуть два существенно отличающиеся друг от друга исхода. Это математическое рассмотрение может иметь много разных интерпретаций - от анализа вероятности (как это сделано в [18]) до проблемы принятия решения.

Варианты соответствующих результатов могут быть обозначены введением чисел 1-0. 1-«да» - первый вариант результата события, 0 – «нет»- второй вариант результата события. Для дальнейшего рассмотрения, однако, целесообразнее ввести изоморфный аналог логистической группы.

 1-первый вариант результата события –«да»,

-1 - второй вариант результата события – «нет».

Предыдущий опыт (“интуицио”) позволяет нам с определенной точностью предсказать степень предпочтительности того или иного результата. До тех пор, пока событие не произошло, мы можем лишь догадываться о том, какой вариант результата будет реализован. Наши догадки, в принципе, могут колебаться между --1 до +1 , при этом колебания обратимы и могут быть охарактеризованы некоторым числом .

Чтобы понять, какую интерпретацию может иметь число , можно привести несколько физических или социологических примеров.

Пусть имеется жёлоб длиной 2 см. В какой-то момент времени на жёлоб положен шарик. Этот момент можно считать началом события. В точках, расположенных от середины жёлоба на расстоянии -1см и +1см, находятся дырочки, в которые может провалиться шарик. Событие состоит в том, что фокусник катает шарик по желобу, стараясь, чтобы шарик не провалился, и продолжается до тех пор, пока шарик не провалится в одну из дырок. Положение шарика по длине жёлоба характеризуется тем самым числом , которое было введено нами выше. Пока шарик не провалился, величина  может принимать любое значение. Все значения  могут быть достижимы.  Когда же шарик провалился в одну из лунок –1 или +1 - событие свершилось. Лунка символизирует один из вариантов результатов события с двумя исходами. Если подобный эксперимент проводить несколько раз, то возникает относительная частота (в пределе при очень больших значениях N, стремящаяся к некоторому числу, называемому нами вероятностью) того, что шарик провалится либо в точку +1 -, где N - общее число экспериментов (процессов), либо в точку -1 . Это утверждение является приближенным и требует более подробного доказательства.

Другой вариант интерпретации представлен в монографии [18]. Там предложен следующий мысленный эксперимент. Допустим, что на некоторый вопрос могут быть даны два ответа “да” или “нет”. Пусть имеется N человек, и все они ….на данный момент находятся в одном и том же состоянии нерешительности. Потребовав немедленного ответа , мы получим N ответов ( +1) и N ответов (-1). Таким образом, можно ввести вероятность (точнее, относительную частоту)  положительного и отрицательного ответов. После совершения события (принятия общего решения) возможны только два варианта - либо 1, либо 0. То есть необратимо происходит изменение вероятности.

Сюда же относится и традиционный эксперимент с бросанием монеты .(роль “да” и “нет”; +1 и -1 играют здесь орел и решка).

Аналогичное рассмотрение может быть проведено в общем (абстрактном) случае. Пусть наше событие имеет два исхода с вероятностями  , где обе вероятности могут принимать значения в диапазоне 0-1. В результате события вероятность изменяется таким образом, что либо =1, либо 0.

Величину  можно представить себе в виде единичного вектора , где . Квадраты проекций вектора на оси  равны соответствующим вероятностям.

Таким образом, выбор того или иного результата события может быть связан с вращением вектора в двумерном пространстве. Возможна и другая интерпретация [18]. Вектором могут быть описаны также колебания в принятии решения той управляющей системы, которая сидит внутри каждой взаимодействующей структуры (или где-то между ними). Эти колебания можно считать обратимыми, мы можем склоняться то к одному, то к другому ответу. «Но если ответ дан, то тем самым мы дали старт развитию необратимых процессов, так что и сам ответ принадлежит к цепочке необратимых событий.»[18].

(Продолжим, следуя [18], наши математические построения.

 Введем в рассмотрение матрицу

Ответ “да” или “нет” соответствует собственному вектору, удовлетворяющему соотношению ,

 

=

Другими словами, принятие решения (или совершение события) соответствует “коллапсу” вектора  либо в вектор (1,0), либо в вектор (0,1). Сам вектор  условимся называть “возможностью“, которая превращается в “исход события” только в результате действия проекционного оператора , который проецирует вектор  в состояние {1,0} c вероятностью  либо в ортогональное ему состояние{0,1}с вероятностью . Соответственно, . Вместо двумерного вектора можно использовать комплексное число . Поскольку ,   можно представить в виде . (Нетрудно видеть, что : т.е комплексно -сопряженному числу. Собственным значениям  соответствуют величины 1 и –1  , Неопределенности перед событием соответствуют просто операции вида , где - “угол поворота” либо к ответу +1, либо к ответу –1.

Итак, мы приходим к комплексному представлению “возможности” в простейшем случае ответов “да” или “нет”.[18]  Совокупность этих ответов естественно назвать “пространством результатов события”.

 

3. Вектор вероятности исходов бифуркационного события с конечным числом исходов.

 

Рассмотрим теперь более сложные пространства результатов события, в частности события с конечным числом возможных результатов. Пусть количество вариантов результатов данного события равно . В результате события реализуется лишь одна из возможностей. Перед событием существует вероятность реализации каждой из возможностей . Сумма вероятностей реализации каждого из указанных исходов равна единице, то есть в результате совершения события будет реализован хотя бы один исход.

.                                                       (5.1)

В результате свершения события вероятность реализации одного из результатов окажется равной 1, а вероятность того, что наступит какой-либо другой исход, окажется равной нулю. Вектор -вероятностный вектор - коллапсирует к одному из единичных векторов, направленных вдоль одной из координат; то есть он коллапсирует к одному из ортов системы координат, сформированных возможными исходами события.

Итак, перед самым событием существует некоторый вектор , характеризующий распределение возможностей реализации тех или иных возможных результатов события. Этот вектор может быть назван вектором вероятности будущего события.

 мерный вектор  перед событием может в принципе принимать любые значения на  - мерном многообразии, имеющем уравнение . Предыдущий опыт может приближенно предсказать точку на многообразии, соответствующую моменту, предшествующему изучаемому нами событию, однако мы не можем предсказать точно, что произойдет в результате события.

Совсем по иному выглядит картина после происшедшего события. Событие произошло. Определенный результат реализовался, остальные не реализовались. Вектор  принял одно из  возможных значений. Можно сказать, что событие подействовало как оператор, резко уменьшивший область допустимых значений вектора  - с  мерного многообразия - до одной из  точек.

То же самое можно сформулировать и по-другому. Соотношения вероятностей попадания системы в одно из возможных состояний до и после события резко изменились. До события система еще имела возможность попасть в любое из допустимых состояний. После события возможность попадания во все состояния, кроме одного, оказались равными нулю.

Наблюдатель системы приобрёл значительную новую информацию не только о новом настоящем, но и о новом будущем системы. Здесь, как и ранее для случая с двумя исходами интуитивно появляется понятие информации как результата отождествления системы, которая до свершения события могла с некоторой вероятностью оказаться в одном из возможных состояний с некоторым конкретным состоянием.

Если считать, что в процессе события точка на  мерном многообразии задана и принимает одно из возможных значений, то после события произошло скатывание этой точки в одну из -наперед заданных точек.

Нашему рассмотрению может быть дана и другая математическая интерпретация. Пусть мы имеем фазовое пространство взаимодействующих структур, имеющее n аттракторов; существует некоторая точка (или область), отделяющая друг от друга бассейны притяжения этих аттракторов . Перед событием фазовое состояние системы взаимодействующих структур попадает в указанную точку или область, выйдя из которой в процессе события она попадает в бассейн притяжения того или иного аттрактора, откуда ей уже не вернуться назад. При этом однако, точка фазовой плоскости может находиться в области неопределенности очень долгое время, не формируя какой либо определенной структуры, то есть вопреки нашему первоначальному предположению само событие может иметь конечную или даже бесконечную длительность. И здесь возникают глубокие вопросы – а не является ли сама эта область структурой в каком–то смысле. Те же проблемы возникают и при рассмотрении странного аттрактора. Хотя в некотором смысле он является аттрактором и указывает на наличие некоторой структуры, однако внутри него все или почти все не определено, а следовательно  бифуркациоонные события при рассмотрении системы, вышедшей на странный аттрактор могут длиться чрезвычайно долго (теоретически бесконечно). С другой стороны именно на такие события легко воздействовать как извне, так и изнутри. Именно они могут представлять основной внутренний механизм управления будущим.

Одним из претендентов на формирование управляющего механизма (контроллера) является странный аттрактор.

Сумма проекций вектора  на соответствующие оси по определению понятия вероятности равна 1. Тем самым модуль вектора  переменен и достигает максимума, равного единице, когда событие произошло. В случае, когда все проекции этого вектора равны между собой, его   модуль оказывается равным .

Интересной математической задачей может служить отыскание -2 мерных многообразий, удовлетворяющих одновременно двум условиям [15]

                                           (5.2)

Система (5.2) представляет собой пересечение в зоне положительных значений всех обобщенных координат гиперплоскости и гиперсферы. Это пересечение должно представлять собой либо полные гиперсферы размерности -2, либо дуги соответствующих гиперсфер.

Рассмотрим частные случаи  этих  многообразий

=2

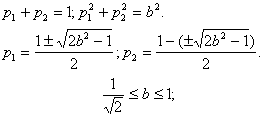
Итак, каждому значению  cоответствует по две точки на прямой линии.

Область определения распределения вероятностей - отрезок прямой линии, лежащий в первом квадранте и отсекающий на осях   отрезки, равные 1.

 

Рассмотрим более сложный случай =3. [15]

Введем замену переменных

 

и подставим новые переменные в уравнение для лини......и пересечения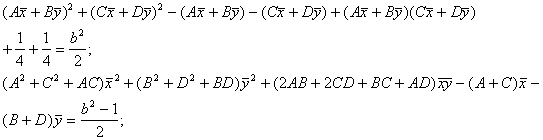  

Полагая ,

получим

.

Введя новую замену переменных , получим

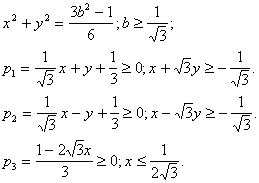
Найдем точки треугольника, начиная с которых все точки окружности  лежат вне пределов допустимых значений.

Коородинаты этих точек равны

.

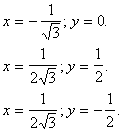Эти точки лежат на окружности

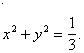
Уравнение окружности, касающейся треугольника:

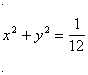
Координаты точек касания

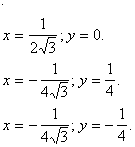
Максимальная окружность, все точки которой  удовлетворяют условию постоянства  имеет радиус .

Ей соответствует величина радиуса сферы .

Итак, имеем окончательно для трех вариантов возможных результатов события. Минимальное допустимое значение  равно . Этому минимальному значению соответствует одна точка, лежащая в центре равностороннего треугольника, граница которого образована пересечением плоскости  с координатными плоскостями.

Линии, соответствующие постоянным значениям  при  представляют собой полные окружности, описываемые уравнением  а координаты вектора  связаны с координатами соотношениями 

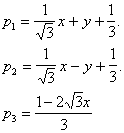
 При этом радиусы окружностей изменяются от нуля до .

При увеличении радиуса сферы и соответственно радиуса окружности зоны постоянных значений  разбиваются на дуги окружностей, которые при =1 вырождаются в три предельные точки,. При этом радиус окружности  .

Если рассматривать полученный треугольник как фазовое пространство некоторой динамической системы, то в этом фазовом пространстве могут быть выделены центр, соответствующий минимуму модуля , и края, соответствующие максимуму модуля. И те и другие точки могут являться аттракторами системы при тех или иных условиях.

Если мы перейдем к большему числу вариантов, то, например, в случае 4-х возможных результатов события вектор  будет уже четырехмерным, а областью задания этого вектора будет тетраэдр. Центр тетраэдра соответствует минимуму , а все четыре возможных варианта результатов события соответствуют четырем точкам множества  являющимся вершинами тетраэдра. Поверхности постоянных значений  представляют собой сферы с центрами в центре тетраэдра. Опять мы имеем одну центральную точку и        дискретное множество из 4-х точек, соответствующих 4 м возможным результатам события.

Нечто подобное можно получить и в общем случае исходов бифуркационного события.

Итак, перед свершением бифуркационного события  модуль вектора вероятности может принимать любое значение , меньшее 1. но большее или равное  , где - число возможных исходов. Минимальное значение модуля вектора соответствует случаю, когда предполагаемые нами вероятности  реализации того  или иного из известных нам исходов бифуркационного события равны между собой. Этот случай соответствует максимальной неопределённости знания о будущем конкретном исходе бифуркационного  события . Всякое изменение вектора  от этого минимального значения, если оно отражает реальные возможности структур, участвующих в событии, уменьшает эту неопределённость, а следовательно увеличивает информацию о будущем исходе события. Наибольшая  информация может быть получена данным конкретным  наблюдателем в случае свершения события, когда величина модуля вектора 

 

4. Элементарная теория вероятностей для бифуркационного события с конечным числом исходов.

 

Этот термин появился в нашем изложении в связи  с тем , что в качестве прототипа мы приняли изложение классической монографии А. Н. Колмогорова [7], однако мы приняли к рассмотрению несколько более общую гипотезу, чем в классической теории вероятностей, которая, в некотором частном случае сводится к классической теории вероятностей. Введение этой гипотезы позволяет , как нам кажется, построить некоторую общую теорию, частными случаями которой окажутся как классическая теория вероятностей, так и квантовая механика, которые, насколько нам известно, не сводятся друг к другу и эта несводимость являлась одной из научных проблем.

 "Относительно того, что твёрдо известно

и не подлежит сомнению,

мы говорим, что знаем или понимаем;

 относительно всего прочего - что только

догадываемся или предполагаем.

Делать о какой-либо вещи предположения -

 всё равно, что измерять её вероятность .

Поэтому искусство предположений

(Ars conjectandi sive stohastice)

мы определяем как искусство возможно точнее

измерять вероятности вещей затем,

чтобы в наших суждениях или действиях

мы могли всегда выбирать или следовать тому,

что будет найдено лучшим,

более удовлетворительным,

спокойным и разумным.

В этом единственно заключается вся мудрость

Философа и благоразумие политика.

Я.Бернулли

Базель, 1713 г.

 

Цит. По книге [8] Я. Бернулли "О законе больших чисел", пер. с лат. - М.: Наука. Гл. ред. Физ.мат. лит. 1986. С.27. и по книге [7] 

"Мы назовём элементарной (квантовой) теорией вероятностей ту часть теории вероятностей, в которой приходится иметь дело с вероятностями лишь конечного числа событий. Всякая аксиоматическая (абстрактная) теория допускает, как известно, бесконечное число конкретных интерпретаций. Таким образом, и математическая (квантовая) теория вероятностей допускает наряду с теми интерпретациями, из которых она возникла, также много других. Так мы придём к приложениям (квантовой) математической теории вероятностей к таким  областям науки, которые не имеют отношения к понятиям случая и вероятности в собственном смысле этого слова. "

Аксиомы.

Пусть  конечное множество элементов , которые мы будем называть элементарными исходами бифуркационного (случайного) события, а  множество подмножеств из . Элементы множества  будем называть совокупностями исходов бифуркационного события, а - пространством элементарных исходов бифуркационного события.

 

1.  - является алгеброй множеств.

Система подмножеств множества  называется алгеброй, если , соединение, пересечение и разность двух множеств системы опять принадлежит этой системе. Мы обозначаем пересечение множеств  и через или , их соединение - через , разность - через . Дополнительное множество  к множеству  обозначаем через . Через  обозначается пустое множество. Если множества  и не пересекаются (), то их соединение будет обозначаться также через  и называться суммой. Множества из  будем в дальнейшем обозначать большими латинскими буквами.[7,9]

2.  Каждому элементу   из  поставлено в соответствие неотрицательное действительное число - вероятность реализации -того исхода бифуркационного события.

3.  .

 В этом случае говорят, что  суть вероятности элементарных исходов  или просто элементарные вероятности.

Терминологические замечания

Мы определили объекты нашего дальнейшего изучения  -совокупности  элементарных исходов  бифуркационного (случайного) события - как множества. Многие теоретико- множественные понятия будут обозначаться в квантовой теории бифуркационных событий и процессов другими именами. Мы приведём здесь краткий указатель таких понятий

 

В теории множеств                                        Для бифуркационных событий.

1.   и не пересекаются (),    1. Совокупности исх одов  и

                                                                      несовместны.

2.                               2. Совокупности исходов ,,…

                                                                    несовместны.

3.                                             3. Совокупность исходов  

                                                                    построена по общим элементам

                                                                    совокупностей

 4.                                 4. Совокупность исходов   

                                                                      содержит все элементы,

                                                            входящие в совокупности исходов                   ,,  ,

   5..Дополнительное множество .  5. -Противопложная совокупность

4.                                                                     исходов

                            элементарного исхода, входящего в совокупность

                                                                 исходов

6.                                                     6. - невозможно - то есть не   содержит

                                                      ни одного из возможных элементарных исходов.

7.                                          7. Хотя бы один из исходов, входящих в -

                                                               должен необходимо наступить.

8.Система   множеств       8. Анализ бифуркационного события

образует разложение множества ,       состоит в том, что устанавливают ,

если (это уже            какая из совокупности исходов

предполагает, что множества  попарно  реализуется  в результате

не пересекаются.)                                          свершения события.

                                                                        называются при этом возможными

                                                                        совокупностями исходов события .

9. является подмножеством :.9.Все исходы, входящие в совокупность

                                                                       исходов   входят и в совокупность

                                                                       исходов .

 

4.Каждому множеству   из  поставлено в соответствие неотрицательное действительное число . Это число называется вероятностью реализации совокупности исходов .  Оно определяется как сумма вероятностей элементарных исходов, входящих в .

,

где  - номера элементарных исходов , входящих в совокупность  

 

Из аксиомы (3) следует, что

Если  и  не пересекаются, то

Совокупность объектов , удовлетворяющую аксиомам (1-4) будем называть конечным полем вероятностей.

Наша система аксиом 1-4 непротиворечива. Это показывает следующий пример:  состоит из единственного элемента ,  из  и пустого множества , при этом положено .

Наша система аксиом , однако, не является полной: в разных вопросах теории вероятностей и квантовой теории рассматриваются различные поля вероятностей.

П.4. Непосредственные следствия из аксиом, условные вероятности, теорема Байеса.

Из   и аксиомы (5) следует, что в случае разбиения   

                . (1)

и

               . (2)

Так как , то, в частности ,

                                                    . (3)

Если  несовместны, то из аксиомы IV следует формула

 (4)

(теорема сложения).

Если ,  то частное

 

       (5)

называется условной вероятностью совокупности исходов  при условии реализации совокупности исходов .

Из 5 непосредственно следует , что

 

 (6)

Заключение по индукции даёт общую формулу

 (7)

 (теорема умножения).

Легко доказываются также следующие формулы:

 

, (8)

, (9)

(10)

 

Сравнивая формулы (8)-(10) с аксиомами (1-4), получаем, что система множеств  вместе с функцией множеств  (при закреплённом множестве ) образует поле вероятностей. Следовательно, все доказанные для вероятностей

 общие теоремы справедливы для условных вероятностей  (при фиксированной совокупности исходов ). Легко также заметить, что

                                                      (11)

Из (6) и из аналогичной формулы

 получаем важную формулу

,                              (12)

содержащую, собственно  теорему Байеса.

Теорема (о полной вероятности). Пусть  и - произвольная совокупность исходов.

Тогда

                            (13)

 

Доказательство:

Поскольку

, то, согласно (4)

;

согласно (6) при этом имеет место равенство

 

Теорема (Байеса) Пусть  и - произвольная совокупность исходов.

Тогда

 

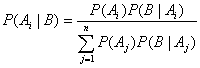                                                                (14)

Доказательство. Согласно формуле (12) ,

.

Для получения формулы (14) остаётся только заменить вероятность её выражением (13) по теореме о полной вероятности.

 

4..Событие с конечным числом исходов. Введение амплитуды вероятности.

Вернёмся теперь к рассмотрению более общего случая, когда бифуркационное событие имеет  возможных исходов. Вектор , где можно ввести и в этом случае. Фактически его введение, позволяющее вместо некоторой аддитивной меры,  рассматривать метрический вектор единичной длины в евклидовом пространстве, просто эквивалентно взаимно однозначной замене переменных.

В этом случае вся изложенная выше теория может быть переформулирована в терминах амплитуды вероятности.

    Каждому множеству   из  может быть поставлено в соответствие неотрицательное действительное число . Это число называется  амплитудой вероятности реализации совокупности исходов .  Оно определяется как корень квадратный из суммы квадратов амплитуд вероятности элементарных исходов, входящих в .

,

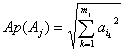где  - номера элементарных исходов , входящих в совокупность  

Из аксиомы (3) следует , что

.

Если  и  не пересекаются, то

Каждому множеству  , состоящему из  элементарных исходов бифуркационного события, соответствует некоторый  - мерный евклидов вектор  . , модуль которого равняется  .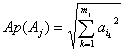

При этом разложение множества  на  сумму взаимно не пересекающихся  множеств эквивалентно разложению вектора  на сумму взаимно ортогональных векторов, каждый из которых имеет координаты, соответствующие  элементарным событиям, входящим в множество, которое он характеризует, - орт координаты, характеризующей i-тый элементарный возможный исход бифуркационного события.

 .

Совокупность объектов  или , удовлетворяющую аксиомам (1-4) будем называть конечным полем  амплитуд вероятностей .

Наша система аксиом 1-4 непротиворечива. Это показывает следующий пример:  состоит из единственного элемента ,  из  и пустого множества , при этом положено .

Наша система аксиом, однако, не является полной: в разных вопросах теории вероятностей и квантовой теории рассматриваются различные поля амплитуд вероятностей.

П.4. Непосредственные сведения из аксиом, условные вероятности, теорема Байеса.

Из   и аксиомы (5) следует, что в случае разбиения   

                . (1)

и

                (2)

Так как , то, в частности ,

                                                    . (3)

Если  несовместны, то из аксиомы IV следует формула

 

 (4)

 или эквивалентная ей

(4а)

(теорема сложения).

Если ,  то частное

 

       (5)

называется условной  амплитудой вероятности совокупности исходов  при условии реализации совокупности исходов .

Из 5 непосредственно следует , что

 

 (6)

Заключение по индукции даёт общую формулу

 (7)

 (теорема умножения амплитуд).

Легко доказываются также следующие формулы:

 

,                                                                                         (8)

,                                                                                          (9)

                                   (10)

 

Сравнивая формулы (8)-(10) с аксиомами (1-4) получаем, что система множеств  вместе с функцией множеств  (при закреплённом множестве ) образует поле вероятностей. Следовательно, все доказанные для вероятностей

 общие теоремы справедливы для условных вероятностей  (при фиксированной совокупности исходов ). Легко также заметить, что

                                                    (11)

Из (6) и из аналогичной формулы

 получаем важную формулу

,                              (12)

содержащую, собственно  теорему Байеса.

Теорема (о полной амплитуде вероятности). Пусть  и - произвольная совокупность исходов.

Тогда

                            (13)

 

Доказательство:

Поскольку

, то, согласно (4)

;

согласно (6) при этом имеет место равенство

 

Теорема (Байеса) Пусть  и - произвольная совокупность исходов.

Тогда

 

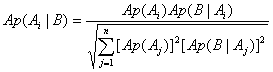                                                               (14)

Доказательство. Согласно формуле (12) ,

.

Для получения формулы (14) остаётся только заменить вероятность её выражением (13) по теореме о полной вероятности.

  

5. Случайные величины и их возможная связь с параметром целого

 .

П. 1 Вероятностные функции.

Пусть дано отображение множества  в множество , состоящее из каких-либо элементов, т.е. определённая на  однозначная функция , значения которой принадлежат множеству . Каждому подмножеству  из  мы ставим в соответствие в качестве его прообраза в  множество  элементов из , которые отображаются в один из элементов . Пусть далее  система всех подмножеств из , прообразы которых принадлежат к алгебре множеств . Система  тогда также является алгеброй. Мы полагаем теперь

                                                 (1)

 

 или, что эквивалентно

                                             (1а)

Эта определённая на  функция множеств  удовлетворяет относительно алгебры всем нашим аксиомам. И, следовательно, является вероятностной функцией на .

Определение.

Пусть дана однозначная функция  бифуркационного события . Тогда функция  определённая формулой (1) называется вероятностной функцией , а функция  амплитудой вероятностной функции .

 

 Примечание 1 При исследовании поля вероятностей ( функцию  называют вероятностной функцией или просто вероятностью, а  вероятностной функцией . В случае   совпадает с  .

Аналогичное утверждения может быть сделано относительно соответствующих амплитуд.

Примечание 1 При исследовании поля вероятностей ( функцию  называют амплитудой вероятностной функции или просто амплитудой вероятности, а амплитудой вероятностной функции . В случае   совпадает с  .

Примечание 2. Совокупность исходов бифуркационного события  состоит в том, что  принадлежит множеству . Следовательно,  есть вероятность того, что  , а  - амплитуда этой вероятности.

Нам осталось доказать вышеупомянутые свойства .Они следуют, однако, из одного единственного факта, а именно, следующего.

Лемма. Сумма, пересечение и разность каких либо прообразных множеств  являются прообразами соответствующих сумм, пересечений и разностей множеств .

Доказательство проведем для сумм. Пусть множества  и  являются прообразами множеств  и . Образуем новое множество .

Любая точка этого множества, после отображения  попадет либо в множество , либо в множество , а следовательно, её отображение будет принадлежать множеству . Ни одна точка , не принадлежащая  не попадёт при отображении ни в  ни в , а следовательно, не будет принадлежать . Таким образом , лемма доказана.

 

Пусть теперь  и  два множества из их прообразы  и  принадлежат тогда . Так как - алгебра, то множества , и  также принадлежат к . Но эти множества являются прообразами множеств ,, , следовательно, последние множества принадлежат к . Итак, мы доказали, что - алгебра.

Далее ясно, что 

Что  и  всегда неотрицательны, понятно само собой. Следовательно остаётся доказать, что   аддитивна, а - квадратично суммируема.

Итак, пусть множества  , а следовательно, и их прообразы  не пересекаются. Тогда

,

чем доказана аддитивность .

Последняя формула совместно с выражением  через  позволяет получить соотношение для квадратичной аддитивности .

 В заключение заметим следующее (что окажется важным при последующем рассмотрении) . Пусть  -функция, отображающая   в . , а  другая функция, отображающая   в . Тогда сложная функция   отображает множество   в . Мы рассмотрим теперь вероятностные функции и  для функций  и . Эти две вероятностные функции связаны, как легко подсчитать, следующим соотношением:

                                                    (2)

 

П.2 Определение случайных величин, функции распределения.

Определение 1. Однозначную действительную функцию , определённую на основном множестве , называют случайной величиной , если при каждом выборе действительного числа  множество  всех тех  , для которых справедливо неравенство  принадлежит к системе множеств

Эта функция  отображает основное множество  на множество  всех действительных чисел. Наше определение случайной величины можно теперь сформулировать так: действительная функция  является случайной величиной тогда и только тогда, когда   содержит каждый интервал вида

Так как  - алгебра, то она содержит наряду, с интервалами  также всевозможные конечные суммы полуоткрытых интервалов . Вероятностная функция  случайной величины  определена для всех множеств  алгебры .

 

 

Определение II.

Функция ,

Где  и  допускаются в качестве значений  называется функцией распределения случайной величины .

 Из определения непосредственно следует, что

 

                           (1)

Вероятность выполнения неравенства  , очевидно, задаётся формулой

               (2)

Отсюда следует, что для

Это значит, что  неубывающая функция.

Пусть далее , тогда

.

Следовательно, согласно аксиоме непрерывности

 стремится к нулю при . Отсюда видно, что функция  непрерывна слева.

Аналогично можно доказать, что

,                                      (3)

                                                     .                                       (4)

 

 

Действие и фаза.

Предположим теперь, что каждому элементарному исходу бифуркационного события  соответствует некоторая действительная величина ,  изменяющаяся от   до , характеризующая интегральные свойства исследуемой системы  (частный случай случайной переменной). Тогда каждому элементу конечного множества  можно ввести в соответствие две величины:

амплитуду вероятности  и величину  , которую по аналогии с квантовой механикой можно назвать действием системы. Если некоторые свойства состояний системы являются периодическими функциями от , с периодом , то вместо величины  можно ввести спиральную переменную [1], путём  отображения прямой линии  на цилиндричеcкую круговую спираль с основанием цилиндра единичного радиуса.

Эта спираль может быть описана спиральным комплексным числом с единичным модулем . Проекцией каждого такого числа на комплексную плоскость является точка на окружности единичного радиуса, описываемая алгебраическим комплексным числом , где . Оба  представления переменной , которая может рассматриваться в этом случае как фаза бифуркационного процесса, имеют одинаковые права на существование и будут нами в дальнейшем использоваться.

Предложенное представление является обобщением введённой нами ранее случайной переменой ь на случай периодических или волновых процессов  (возможны дальнейшие обобщения за счёт введения в рассмотрение детерминированной или случайной зависимости периода  от значения переменной , которые путем замены переменных могут быть сведены к рассматриваемому нами случаю). В случае  возвращаемся к первоначальному варианту случайной переменной и к классической теории вероятностей.

Однако, указанное представление, обладая большей общностью, позволит нам в дальнейшем перейти к рассмотрению процессов, аналогичных процессам, изучаемым квантовой, и в случае, когда значения   значительно больше - к классическому и квазиклассическому приближениям.

Варианты же с переменной  или случайной величиной  вводят нас в область математического описания биологических и социальных процессов;

Поэтому в дальнейшем будем рассматривать именно это представление, имея в виду его наиболее широко распространённые приближённые частные случаи.

О связи принятого нами представления с параметром целого и волновыми свойствами исследуемых систем следует поговорить особо, так как физическая интерпретация указанных параметров может быть различной для волновых структур и систем, принадлежащих к различным классам. 

6. Введение в рассмотрение комплексного волнового вектора

.

Следующим шагом в нашем анализе бифуркационного события будет введение в рассмотрение, по аналогии с действительным вектором вероятности, комплексного волнового вектора .  Этот вектор, в частном случае, будет волновым вектором квантовой механики).

        

Это самое сильное допущение в наших рассуждениях.

 

     Рассмотрим первоначально отдельные компоненты этого вектора. Для этой цели каждому состоянию - каждому элементарному исходу бифуркационного события сопоставим не два отдельных числа, а одно комплексное число, равное их произведению действительного числа  на экспоненту мнимой единицы и на величину действия. Кроме того, каждому исходу  бифуркационного события (каждому элементу) сопоставим единичный направленный вектор , направленный вдоль оси абсцисс комплексной плоскости  . В этом случае можно ввести собственный волновой вектор данного исхода бифуркационного события , принимающий значения в любой точке единичного круга комплексной области , включая его центр (в случае невозможности данного исхода) и окружность единичного радиуса (в случае неотвратимости наступления события). Наряду с этим вводим единичный комплексный собственный вектор

Сумма комплексных волновых векторов для всего конечного множества возможных исходов формирует полный волновой вектор бифуркационного события, или волновой вектор возможных состояний системы. 

 

В соответствии с основными введёнными нами аксиомами волновой вектор   

обладает  рядом свойств, следующих из данных определений

 ,

где  величины, комплексно сопряжённые величинам .

В этом случае выписанные ранее аксиомы теории вероятностей могут быть выражены через собственные волновые векторы исходов  события.

 

5.  Каждому элементу   из  поставлен в соответствие комплексный вектор

Тогда распределение амплитуд вероятностей реализации и действия между исходами бифуркационного события может быть записано в виде единого вектора  с комплексными компонентами

 

3. .

 В этом случае говорят, что  суть амплитуды вероятности  элементарных исходов  или просто элементарные амплитуды вероятности,  

 

Каждому множеству  , состоящему из  элементарных исходов бифуркационного события, соответствует некоторый  - мерный евклидов вектор , модуль которого равняется  .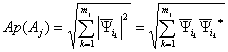

При этом разложение множества  на  сумму взаимно не пересекающихся  множеств эквивалентно разложению вектора  на сумму взаимно ортогональных векторов, каждый из которых имеет координаты, соответствующие  элементарным исходам, входящим в множество, которое он характеризует, - орт абсциссы комплексной плоскости , характеризующей i-тый элементарный возможный исход бифуркационного события.

 

 Тем самым мы формально ввели в рассмотрение совокупности исходов бифуркационного события комплексный вектор, анализ которого не заставляет отказываться от основных аксиом  теории вероятностей и который позволяет описывать единым образом вероятностные и физические параметры каждого возможного исхода бифуркационного события.

Единственным практическим основанием для введения такого вектора является тот факт, что он оказался необходимым при построении математических моделей квантовой механики.  Однако во введении этого вектора, по-видимому, должен существовать некий более глубокий физический смысл. Этот комплексный вектор должен, как подсказывает интуиция, играть роль не только квантовой механике, но и в природе вообще, значительно более важную роль, чем это кажется на первый взгляд.

 

6. Идентификация элементарных исходов бифуркационного события.

 

Попытаемся вернуться  к анализу физических явлений, данных нам в ощущениях. Поставим вопрос таким образом. А как же мы различаем между собой  элементарные возможные исходы? И какие вообще возможные исходы можно считать элементарными? На этот вопрос наши математические построения не дают ответа. Ведь определение параметров (в частности) действия того или иного исхода происходит всегда  с некоторой погрешностью. И мы никогда  не знаем, сколько различных возможностей мы упустили. Возможно и бесконечное число. Поэтому постулирование определённых элементарных исходов, на котором базировалось все наше построение, является лишь грубым приближением к действительности. Эту проблему не полностью решает и переход в рамках классической теории вероятностей и квантовой механики к бесконечным полям вероятностей, о чём  мы будем говорить позднее. Для полного решения этой проблемы необходимо установить то или иное правдоподобное правило перехода от одного множества  со своими элементарными исходами событий , описывающего исходы данного события, к другому вероятностному множеству  с элементарными событиями ,  описывающему исходы того же события. Тем самым мы делаем приемлемыми оба указанных представления и в рамках соответствующей математики определяем возможность и правомочность различных возможных представлений групп исходов данного события.

В случае, если все исходы имеют одинаковое действие, можно вернуться к первоначальной аксиоматике и просто отображать соответствующие разбиения множества  на множества, число элементов которых равно числу элементов разбиения первоначального множества. При этом в качестве элементарных вероятностей нового разбиения можно принять суммарную вероятность реализации совокупности старых исходов. В этом случае необходимость идентификации не требует никаких новых рассмотрений.

     Однако, в случае, если мы хотим идентифицировать исходы, имеющие различные значения действия, и привести их к элементарным, то необходимо ввести какое-либо другое правило, которое даст нам возможность более обоснованно не только вводить за счёт идентификации новые элементарные исходы, но и определять погрешность, которая возникнет при таком введении за счёт неадекватного ("неправильного") отождествления.

    При таком отождествлении необходимо учитывать не только вероятности отождествляемых элементарных исходов события, но и различие мер их определяющих, в частности , различные значения действия. Одним из возможных способов такого отождествления является отождествление с использованием введенного нами комплексного волнового вектора.  Как мы  видели, каждому элементарному исходу бифуркационного события можно ввести в соответствие собственный комплексный волновой  вектор, отражающий как вероятностные, так и материальные свойства объекта (хотя пока и непонятно каким образом).

Как мы видели ранее, при обычном объединении возможных исходов можно ввести новый многокомпонентный действительный вектор амплитуды вероятности, для которого амплитуды вероятности каждого элементарного исхода окажутся проекциями на ортогональные оси координат в евклидовом пространстве., а амплитуда вероятности совокупности исходов определяется как модуль этого вектора. Такой тип идентификации справедлив и возможен в случае, когда действия структур равны между собой. Поэтому в общем случае целесообразно ввести аналогичную процедуру для комплексных волновых векторов. Как мы уже указывали ранее, некоторой совокупности исходов можно ввести в соответствие не действительный вектор амплитуды вероятности, а комплексный волновой вектор. Этот вектор можно также считать разложенным на комплексные ортогональные координаты, проекцией его на которые являются соответствующие собственные волновые векторы.

 

    1.Первая аксиома идентификации.

 

Вводимый нами принцип идентификации (аналог введения фактор-пространства и изоморфизма вероятностных пространств) состоит в том, что если в качестве нового элементарного исхода события будет принята данная совокупность элементарных исходов событий , то её волновой вектор будет определяться как корень степени  из суммы степеней  волновых векторов, входящих в  данную совокупность исходов, умноженный на единичный орт новой комплексной идентификационной координаты и на некоторую постоянную, алгоритм определения которой будет дан нами ниже.

 или в частном случае

           

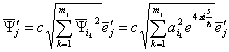
 Эта последняя  формула может быть названа первой аксиомой идентификации порядка .(или, в частном случае, квадратичной идентификации, если =2)

   

2. Вторая аксиома идентификации. 

 

Физический смысл  действительной постоянной  и способ её определения будут определены нами путём введения второй аксиомы идентификации.

 Пусть мы выбрали некоторое разбиение вероятностного множества  на  подмножеств . Затем осуществляем отображение множества  на множество , состоящее из  элементов , каждый из которых является образом в множестве  совокупности исходов .

В соответствии с первой аксиомой идентификации каждому элементу множества  может быть сопоставлен комплексный вектор

 

 или, в частном случае,

.

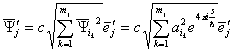 При этом будем считать, что величина  является константой для данного разбиения. То есть  при данном поле вероятности   есть функция от  разбиения 

Она определяется из условия полноты вероятностного пространства , полученного после идентификации.

 или

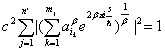 или , в частном случае

 Отсюда следует, что

 

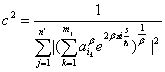
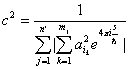
а сама величина  определяется следующей формулой

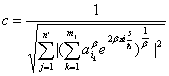 или в частном случае

.

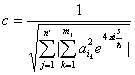Подставляя последнюю формулу в выражение для величины

,

получаем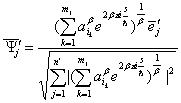

.

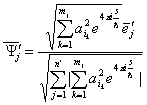Тогда вероятность реализации нового элементарного исхода бифуркационного события определяется  по формуле

 

Или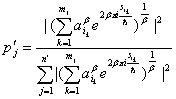

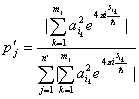
Эта последняя формула является следствием обеих  теорем идентификации.

После выполнения идентификации можно в новом вероятностном пространстве вводить всю совокупность аксиом теории вероятностей, введя  для каждого разбиения , новое квантовое  вероятностное пространство , где для каждого множества  вводится новое значение

 по старым правилам.

Итак, пусть - квантовое вероятностное пространство, а - его измеримое разбиение. Идентифицированным пространством пространства по разбиению  называется вероятностное пространство  , где- это множество элементов разбиения , -алгебра  образована всеми  измеримыми  множествами, а случайная величина  и мера  определяются на основании двух вышеизложенных аксиом идентификации  и их следствий.

 

Возникает вопрос , а как же соотносится введённая нами процедура с уже известными математическими процедурами теории вероятностей и квантовой механики. Именно ответ на этот вопрос частично решит проблему целесообразности столь сложных построений и возможностей выбора величины .

Рассмотрим простейший частный случай, когда действия всех возможных исходов данного  события равны между собой. В этом случае формулы для идентифицированных разбиений имеют вид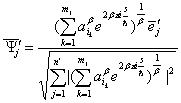

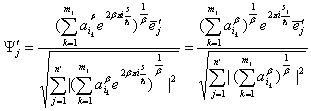
Если мы хотим, чтобы в этом случае выполнялось условие факторизации, то необходимо принять равным двум. Однако , в общем случае это необязательно и в качестве идентификации можно использовать произвольное число  в этом случае факторизация становится просто частным случаем идентификации при   равном 2.

 

 

.

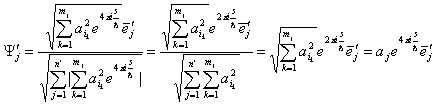Отсюда следует, что в этом частном случае векторы   становятся пропорциональными  векторам  с одним постоянным комплексным коэффициентом . Идентификация вероятностного пространства  по данному разбиению становится эквивалентным факторизации вероятностного пространства. Вероятности идентифицированных множеств остаются аддитивными функциями на всех разбиениях. Идентификация пространства   оказывается эквивалентной факторизации пространства .

Для такой идентификации становятся справедливыми все законы факторизации

 И аксиомы идентификации становятся частным случаем основных аксиом теории вероятностей. Мы возвращаемся к классической теории вероятностей.  

Существует несколько более общих вариантов идентификации с коэффициентом , когда она оказывается во многом эквивалентной факторизации вероятностных пространств. Один из таких вариантов состоит в следующем. Пусть все значения действия равны между собой по модулю ;

 

В этом случае  так же, как и в первом, значения алгебраических комплексных чисел, входящих в собственные векторы всех возможных исходов бифуркационного события, оказываются равными между собой и формула

 

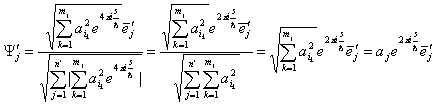
 превращается в формулу

 

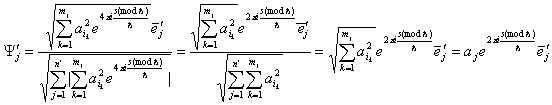
Это последнее выражение характеризует алгебраическую форму идентифицированного волнового вектора. Однако, здесь встаёт проблема , полное решение которой нам не известно, а какому спиральному комплексному числу соответствует полученное значение волнового вектора.?

Можно, конечно, сказать, что выбор величины , то есть номера витка спирали произволен и не влияет на физические результаты, однако это было бы очень просто. Я думаю, что существуют такие случаи, когда выбор величины  может повлиять на физические процессы, описываемые развиваемой нами математикой. Поэтому уходить от решения этой фундаментальной математической проблемы, которую мы можем назвать проблемой сложения спиральных комплексных чисел, считаю нецелесообразным. Однако, как показывает наш предварительный анализ, в любом случае избежать многозначности и возможности при определенных условиях скачков функции  не представляется возможным. Решение задачи , по-видимому, следует искать в анализе особенностей фазовых интегралов и во введении непрерывных значений .

Однако, независимо от решения указанной проблемы, в алгебраической комплексной плоскости и естественно, на реальной оси, всё в порядке.

Поэтому и в данном случае идентификация приводит в идентифицированном вероятностном пространстве к тем же результатам для амплитуд вероятности  и самих вероятностей , что и обычная факторизация, а именно, становятся справедливыми формулы, следующие из основных аксиом теории вероятностей. 

 

В случае, если разбиение  построено по указанному принципу

Третьим случаем идентификации, эквивалентным факторизации векторных пространств, является важный частный случай факторизации, который как это написано у Колмогорова, определяет понятие случайной величины. Здесь мы будем использовать его в другом контексте.

Пусть  является таким разложением основного множества

 

,

 

а  действие  - действительная функция элементарного события , которая на каждом множестве принимает по модулю  значение .

Тогда функция может быть представлена в виде

 

,

где  -индикатор множества , то есть =1, если , если  .

В этом случае  говорят, что   случайная величина, принимающая на отрезке  конечное число значений . ( В принципе, путём обезразмеривания по , можно отобразить этот отрезок на отрезок  , введя новую переменную действия . Однако, по ряду соображений мы этого делать не будем, так как сама величина  может  иметь существенный физический смысл.

Подобный тип идентификации также оказывается эквивалентным факторизации вероятностного пространства.

Покажем это.  

Общая формула для идентифицированного значения  имеет вид:

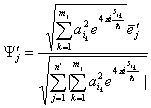
В соответствии со сделанным допущением, для всех , по которым производится по суммам, по которым осуществляется идентифицирование, величины  равны между собой , что позволяет вынести эти величины из под знаков суммы и корня. В этом случае

 

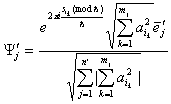
Вследствие аксиомы теории вероятностей величина , равная знаменателю последней формулы , равна 1.

Тогда  для всех идентифицируемых исходов, входящих в множество , а собственный вектор нового идентифицированного элемента  в алгебраической форме будет иметь вид

Здесь 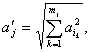 для всех  внутри данного подмножества , а направление вектора   в - мерном комплексном евклидовом пространстве определяется как направление  векторной суммы векторов  

Способ определения величины , как и ранее, остаётся открытым. 

Как и при рассмотрении предыдущих случаев, идентификация и здесь остаётся эквивалентной факторизации пространства  по разбиению .

Этот частный случай идентификации позволяет выйти на обобщение развитой теории на случай произвольных множеств , обладающих тем свойством, что у них имеется естественное разбиение, порождающее конечное множество значений действия. В этом случае идентификация, или , что то же самое , факторизация этого множество, а факторизация таких множеств, если они являются множествами Лебега - является  хорошо исследованным процессом, вновь приводит нас к рассмотренному выше анализу конечного  пространства   , которое оказывается изоморфным совокупности значений .

К этому рассмотрению мы ещё неоднократно вернёмся.

Теперь рассмотрим ещё один частный случай идентификации комплексного вероятностного пространства , именно, для каждого значения , величины  могут быть представлены в следующей форме

, где .

В этом случае общая формула для 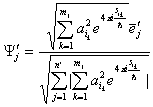 может быть преобразована следующим  образом

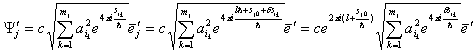
Комплексное число с модулем 1 под знаком корня разлагается вблизи точки   в сходящийся ряд Тейлора

.

Сохраним в этом разложении  четыре первых члена

Подставим последнее разложение в выражение для

.

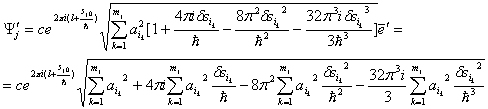Вспомним введённое нами ранее обозначение

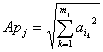
Далее введем в рассмотрение новую величину, относительную амплитуду вероятности   исхода по  отношению к - той  совокупности исходов события.

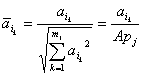
Величины  внутри множества  формируют полную систему амплитуд.

Аналогичные формулы могут быть выписаны для распределений вероятностей.

                                                                  

И совокупность  формируют полное вероятностное пространство.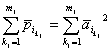

Введём ещё одно обозначение, от введения которого мы ранее отказались

 - относительное избыточное  действие .

Тогда формула для  принимает вид

.

 

,

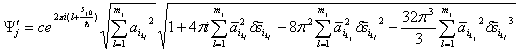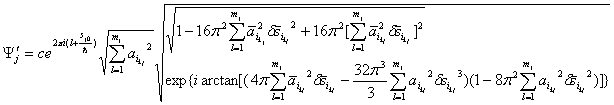
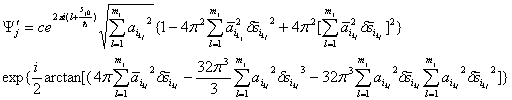
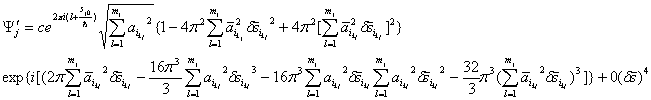
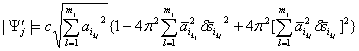
Вспомним вторую аксиому идентификации.

 

.

 

 

 

 

.

 

 

 

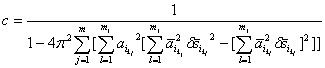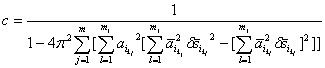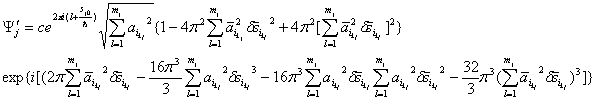
Литература

1.  Басин М.А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. Санкт-Петербург

2.   

Этюд 30

Энтропия и информация бифуркационного события.

 

1. Внешняя энтропия системы

.

    В дальнейшем в нашей методике существенную роль будут играть логарифмы этих чисел, совокупность которых для данной системы можно представить в виде некоторой матрицы, названной нами матрицей энтропии.

    Осреднение собственных чисел матрицы энтропии по всему пространству возможных траекторий (и (или) состояний) системы, рассматриваемой в качестве кванта некоторой обобщённой волны, дает некоторое число, которое может быть названо внешней энтропией системы.

    Приближённое определение этого числа даёт общее представление о степени неопределённости в макроскопическом поведении системы и является важной её характеристикой.

…………………      Однако, величина энтропии зависит от нашего произвола в выборе различных вариантов траекторий и включения системы в обобщённую волну. Поэтому использование этого параметра должно быть выполнено достаточно осторожно.

 

 

    Более разумно принять несколько вариантов разбиений пространства возможных траекторий системы и вычислить несколько значений энтропии.

    Для каждого варианта разбиения можно подсчитать максимальное значение энтропии, соответствующее равномерному распределению вероятностей различных вариантов траекторий.

    Разница между полученным значением энтропии для данной системы и максимальным её значением характеризует при данном числе разбиений информацию о возможном поведении системы

    В качестве пространства разбиений для данной обобщённой волны можно принять поле значений параметра целого.       Если поведение системы с некоторым приближением можно считать детерминированным, то внешняя энтропия процесса, в котором участвует система, может быть принята равной нулю.

При вычислении энтропии процесса необходимо рассматривать несколько возможных вариантов.

Первый вариант  соответствует наличию дискретного набора возможных состояний системы, соответствующих при заданном среднем значении параметра целого нескольким различным вариантам значения этого параметра.  Если вероятности каждого из вариантов заданы или определены эмпирически, то внешняя энтропия системы может для каждого момента внешнего времени, в рамках которого меняется параметр целого системы, определяется однозначно независимо от  параметра целого. В некоторых случаях она может оказаться постоянной величиной для всего исследуемого процесса.

В случае, если возможные состояния системы составляют континуум, такой подход невозможен, так как величина энтропии в этом случае зависит от числа разбиений континуального множества и стремится к бесконечности при увеличении числа таких разбиений. Однако, как было показано нами в     , в этом случае энтропия системы может быть представлена в виде двух составляющих, одна из которых стремится к бесконечности , сохраняя универсальный закон зависимости от числа разбиений, а другая, не зависит от числа разбиений, а лишь от формы кривой распределения вероятности по пространству возможных состояний. Эту последнюю часть и можно принять за внешнюю энтропию системы в этом случае.

 

 

2.Оценка возможных вариантов будущей динамики исследуемой системы.

 Приближённое определение внешней энтропии системы.

. Энтропия и информация, связанные с бифуркационным событием, имеющим конечное число исходов.

Мартин [ ]

Глава 2

 

Энтропия и информация.

 

В этой главе даются формальные определения количества информации, заключённой в случайном событии, и энтропии испытания со счётным числом исходов. Мы также покажем, в каком смысле энтропия является мерой неопределённости, и приведём затем основные свойства информации и энтропии. Далее определение энтропии будет расширено, с тем, чтобы охватить испытания с произвольным числом исходов, а свойства энтропии будут доказаны и для этого случая. Наконец, мы дадим определения скорости создания информации и энтропии динамической системы и установим их наиболее важные свойства. В заключение будет приведено несколько примеров и кратко обсуждены два полезных обобщения этих определений.

 

3.1.                  Информация и неопределённость событий.

 

Пусть - пространство Лебега, а - событие из . Рассматривая  это пространство Лебега как математическую модель некоторого случайного  испытания, положим, что результатом этого испытания явилось событие . Коль скоро мы узнали, что  произошло, тем самым мы получили некоторую информацию. Цель этого раздела состоит в том, чтобы определить в пространстве Лебега функцию , значение которой будет количественной мерой информации, получаемой, если результатом испытания является событие . Неопределённость в наступлении события , имеющаяся до осуществления испытания, должна совпадать с количеством информации, получаемым, если событие  действительно происходит. Таким образом, количество информации, заключённой в событии, будет также служить и количественной мерой неопределённости этого события. 

Определение 2.1.

Информацией или неопределённостью называется вещественнозначная функция событий, зависящая только от вероятностей событий и удовлетворяющая следующим условиям:

2.1.1. Событие , наступающее с вероятностью единица, имеет нулевую неопределённость.

2.1.2. Если одно событие имеет меньшую вероятность, чем другое, то неопределённость первого события больше неопределённости второго.

2.1.3. Неопределённость одновременного наступления двух независимых событий равна сумме их неопределённостей.

 

Насколько это возможно, постараемся теперь выразить количество неопределённости через известные функции. Поскольку  должно зависеть только от вероятностей событий, нам надо найти такую определённую на отрезке [0,1] функцию с вещественными значениями, что если мы положим , то  будет удовлетворять условиям 2.1.1, 2.1.2 и 2.1.3. Легко видеть, что если   монотонно убывает на [0,1] и , то условия 2.1.1 и 2.1.2 выполнены. Остаётся найти условие на , обеспечивающее выполнение 2.1.3.

Пусть события  и независимы. Тогда из 2.1.3 следует, что , поскольку , условие 2.1.3 равносильно равенству .

Таким образом, функция  должна удовлетворять функциональному уравнению

 

                                        (2.1)

 То что монотонные решения уравнения (2.1) исчерпываются кратными натурального логарифма, - классический результат; поэтому мы должны взять . Эта функция обращается в нуль при   для любого значения константы , но является монотонно убывающей лишь при отрицательных .Итак, мы определим  соотношением

                                        (2.2)

где - любое положительное вещественное число, то функция , заданная для всякого события   равенством

                                           (2.3)

обладает всеми свойствами неопределённости. Более того, это единственная функция, удовлетворяющая свойствам, указанным в определении 2.1. 

 

2.2. Информационная функция испытания и энтропия.

 

В первой главе мы видели, каким образом измеримые разбиения некоторого заданного пространства Лебега могут служить математической моделью случайных испытаний. Введём теперь на множестве разбиений информационную функцию, значения которой будут определять количество информации, содержащейся в отвечающих этим разбиениям случайных испытаниях.

Пусть - счётное измеримое разбиение пространства . Через  будем обозначать информационную функцию разбиения - заданную на функцию, значение которой для любого исхода  равно количеству информации, получаемой при реализации содержащего  элемента  разбиения . Таким образом,

                                       (2.4)

где  -обозначает индикатор (характеристическую функцию множества

Исходы отвечающего разбиению  испытания - это элементы . На каждом из них функция принимает постоянное значение, равное количеству информации , получаемой при реализации исхода, или же связанной с этим исходом неопределённости. На языке факторпространств есть функция на факторпространстве , дающая количественную меру неопределённости каждого элементарного  события этого факторпространства.

Ясно, что функция  определена и конечна почти всюду на ; кроме того, она - измерима. Иначе говоря,  случайная величина на пространстве  и в силу неотрицательности для неё определён интеграл ( возможно, имеющий бесконечное значение).

 

Определение. 2.2. Энтропией счётного измеримого разбиения  пространства Лебега  называется математическое ожидание информационной функции разбиения. Энтропия разбиения обозназначается и составляет

 

(мы полагаем  при ).

Таким образом, энтропия счётного разбиения - это среднее количество информации, заключённой в отвечающем разбиению испытании.

 

Теорема 2.3. Если разбиение  имеет элементов, то

Более того,  тогда и только тогда, когда содержит элемент вероятности единица , и  тогда и только тогда, когда - равномерное разбиение , т.е.  для каждого элемента .

Доказательство . Из определения ясно, что , причём  равенство достигается тогда и только тогда , когда  содержит элемент вероятности единица. Для получения другого неравенства заметим, что

Поскольку , причём равенство достигается тогда и только тогда, когда , то .

Таким образом

 И равенство достигается тогда и только тогда, когда  для всех .

Эта теорема объясняет то обстоятельство, что энтропия испытания служит мерой степени его "случайности". Наиболее "случайным" испытанием с  исходами должно быть испытание , в котором все исходы равновероятны. Ему отвечает равномерное разбиение с  элементами, а энтропия таких разбиений максимальна. Наименее случайным испытанием должно быть такое, в котором наверняка происходит некоторое конкретное событие.

Терема 2.3.также позволяет нам интерпретировать и число . Если некоторое испытание имеет  исходов, то его неопределённость не превосходит

 .Поэтому если положить   , то энтропия такого испытания не будет превосходить 1, причём это значение достигается для наиболее случайного распределения  исходов. Таким образом, можно сказать, что для испытаний с  исходами за единицу измерения неопределённости принимается неопределённость испытания с самым случайным распределением исходов. Тем самым , выбор значения определяет выбор единицы неопределённости. Заметим, что  , так что если количество информации выражается через логарифмы по основанию , т. е. если  то единица неопределённости основана на испытаниях с  исходами. Поскольку наименьшее нетривиальное пространство исходов (или разбиение)должно содержать два элемента, информация и энтропия весьма часто определяются с помощью логарифмов  по основанию 2. Связанная с этим основанием единица количества информации называется битом.

Рассмотрим для примера испытание, заключающееся в извлечении разноцветных шаров из урны, содержащей 3 красных, 2 белых и 5 синих шаров. Этому испытанию отвечает разбиение единичного отрезка на 3 отрезка длины 0.3, 0.2, 0.5 соответственно; измеряя в битах, получаем.

 

 

 

и

В этой книге выбор единицы измерения количества информации является, как правило, несущественным, и мы будем считать . Иногда единицы измерения, получающеся при этом значении , называют натами, поскольку в их определении используют натуральные логарифмы. Для перехода от натов к единицам, основанным на испытаниях с исходами, достаточно умножить на   ; так, например, для перехода от натов к битам надо умножать на   

Итак, информационная функция счётного разбиения  пространства Лебега  обозначается через  и определяется равенством

.                                (2.5)

Энтропия разбиения обозначается через  и имеет значение

                                     (2.6).

 

 

   

 

    В некоторых случаях целесообразно объединить действительный параметр целого, для которого в этом случае необходимо брать его среднее значение,  и рассчитанное значение внешней энтропии в области возможных значений параметра целого в единый комплексный параметр, который назван нами комплексным параметром целого или обобщённым параметром Планка. Действительной частью этого параметра служит действительный параметр целого, а мнимой – вычисленное на основе анализа поведения ряда аналогичных систем значение внешней энтропии системы.

    Как следует из предыдущего пункта, в вычислении энтропии существует произвол, определяемый выбором пространства возможных вариантов и разбиением этого пространства.

    Введение комплексного параметра целого позволяет на только убрать этот произвол, но и разработать возможную методологию теоретического вычисления внешней энтропии бифуркационного процесса, не пользуясь зкспериментальными данными, то есть выбора наиболее рационального разбиения пространства возможных состояний.

    Этот подход является прямым следствием допущения о возможности комплексификации параметра целого.

    Может быть предложен следующий возможный алгоритм вычисления значения мнимой части обобщённого параметра Планка.

    Из пунктов 7-10 строится дифференциальное уравнение или итерационный процесс для действительного параметра целого и ищется их решение. Далее осуществляется их комплексификация искомой функции таким образом, чтобы реальная часть комплексного уравнения и решения соответствовали действительному уравнению для параметра целого. Тогда мнимая часть комплексного решения может быть отождествлена с внешней энтропией системы.

    Эта гипотеза  в некоторых случаях позволит снять неопределённость в определении внешней энтропии системы.

    Вообще, комплексификация уравнений, итерационных соотношений и функций во многих случаях позволяет получить принципиально новые результаты, что многократно подтверждалось историей науки.

    Введение обобщённого параметра Планка и комплексификация уравнений, описывающих динамику объекта, приводит нас к построению комплексных моделей и необходимости интерпретации не только действительных, но и мнимых величин, которым в большинстве случаев оказывается возможным придать физический смысл. Иногда комплексификация приводит к резкому упрощению задачи. Но практически всегда введение комплексной переменной позволяет по-новому взглянуть на физические процессы, происходящие с изучаемой нами системой.

 

 

.

Связь между векторами  и  осуществляется с помощью соотношения . Предположим, что мы знаем вектор . Из последнего равенства следует, что любой комплексный вектор  с комплексными компонентами , модули которых равны , может удовлетворять поставленному нами условию распределения вероятностей. Это значит, что уравнение, которому должен удовлетворять вектор , должно быть инвариантно относительно преобразований , матрица которых имеет вид:

 

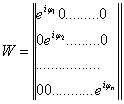
Таким образом, если мы нашли одно из значений вектора , то мы можем вычислить все остальные его значения, определяющие то же распределение возможностей осуществления различных вариантов исходов события. Пусть известно одно из значений вектора . Оно всегда может быть найдено как вектор , состоящий только из положительных действительных координат

Тогда любой комплексный вектор , удовлетворяющий тому же распределению вероятностей, может быть представлен в виде . И обратно .

С другой стороны  - каждому вектору  соответствуют  векторов

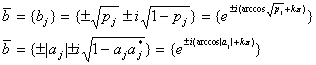
Последняя формула дает соотношение, указывающее на связь между введенными нами комплексными величинами, отражающими бифуркационную характеристику события.

Знание волновых векторов каждого события, входящего в проекцию графа истории системы на вероятностную ось, позволяет построить соответствующий вектор для  двух любых моментов времени, одним из которых является «настоящий» момент, а другим либо какой-либо момент из прошлого,  либо какой-либо момент из будущего, и позволяет принципиально вычислить вероятности  получения того или иного результата цепочки событий .

,

где -значение  вероятности реализации в результате цепочки  событий совокупности структур, соответствующей i-тому исходу цепочки событий.

Отметим три особенности указанного процесса.

1)   Вся процедура определения вероятности  существеннейшим образом зависит от двух моментов времени: момента времени, в который мы  непосредственно анализируем ситуацию, и момента времени, в который мы должны эту ситуацию предсказывать.

2)   Полностью аналогичным образом можно проанализировать прошлые события и определить их вероятности, однако вероятностные соотношения здесь будут иными .

3)   Особенностью подобного рассмотрения является переменность во времени не только значений координат вектора , но и числа существенных компонент этого вектора. В момент нахождения наблюдателя на одной из бифуркационных линий графа структур и событий системы, вне точки, соответствующей происходящему событию, вектор  может считаться одномерным комплексным вектором и модуль значения его комплексной компоненты равен 1. Однако, это утверждение не справедливо для момента времени, когда событие происходит. В этот момент он может иметь n+1 компоненту, где n – число возможных исходов данного события. Если волновые векторы всех событий, входящих в граф, известны, то, выбрав какой–либо начальный момент, мы можем определить вектор вероятности существования той или иной совокупности структур  в любой другой момент в прошлом и будущем.

Здесь возникает проблема индивидуального и общего. Каждая конкретная система взаимодействующих структур обладает индивидуальностью, позволяющей ей в каждый момент времени менять вероятность реализации будущих состояний и выбирать тот результат события, который ее больше всего устраивает.

Волновая функция для группы идентичных систем и волновая функция для отдельной системы существенно отличаются, но связаны между собой. Эту связь должен осуществлять некий механизм выбора (контроллер), определяющий именно для данной системы тот или иной исход события. При этом рассмотрение серии  почти идентичных систем часто дают более не менее устойчивую статистическую картину.

Другой, не менее  интересной проблемой, является определение момента начала события. К этой проблеме можно подойти следующим образом. Пусть сам момент начала события нам неизвестен. Однако, мы знаем, что в какой то момент времени появляется вероятность реализации превращения системы в нечто новое. Тогда, введя в вектор  новую координату, соответствующую состоянию системы перед событием, мы можем весь подготовительный период описывать n+1 мерным вектором , который до начала события имеет одну единичную координату , а затем появляются n новых, величины которых растут до значений, соответствующих вероятностям реализации тех или иных результатов события. Тем самым мы делаем вектор – волновой вектор гладко зависящим от времени, что позволит нам в дальнейшем написать для его определения некоторое дифференциальное равенство.

Если перейти к построению зависимости векторной функции  той или иной системы от времени, то здесь необходимо говорить о необходимости параллельного построения как минимум трех различных функций.

  1) Волновой функции настоящего, соответствующей настоящему моменту времени . Эта функция, в случае, если рассматривается момент, в который не происходит никакое бифуркационное событие, имеет всего лишь одну компоненту. Однако, это вовсе не значит, что векторная функция настоящего никогда не может иметь большого и даже бесконечного числа компонент, ведь число одновременно происходящих подсобытий может быть и большим, и даже бесконечным.

2)Волновой функции будущего , характеризующей вероятности реализации в будущем того или иного результата цепочки событий. При этом всегда число компонент вектора  больше или равно числу компонент вектора , однако совершенно не обязательно, чтобы оно равнялось или было больше числа компонент вектора , так как в будущем может произойти, в частности, тот вариант, что все возможные состояния системы сойдутся к одному аттрактору (здесь вновь целесообразно вспомнить метафору дороги и автомобиля).

3) Волновой функцией прошлого , характеризующей доступные в настоящий момент времени знания о прошлом. При этом размерность больше или равна размерности , но вовсе не обязательно больше или равна размерности .

  Знание значений векторной функции   в любой момент времени не означает, что мы знаем реальную траекторию будущего события. Можно сказать, что если мы сумели правильно выстроить ветвь графа, соответствующую будущему, то реально, процесс пройдет по одному из направлений построенного нами графа. С изменением момента времени  на момент времени  cостояние системы меняется. Реальное значение функции  существенно отличается от значения функции , а следовательно будет существенно отличаться от

Да, мы с определенной вероятностью можем предсказывать будущие события или цепочки событий, однако, в следующий момент времени, когда произошло что-то из предсказанного нами, все вероятности меняются и наше предсказание будущего требует непрерывной корректировки.

Фактически в каждый момент времени мы приобретаем новую информацию, а следовательно, узнаем о будущем больше и можем с большей вероятностью предсказать то, что реально произойдет.

Нечто аналогичное, но по другому происходит при обращении в прошлое.

Здесь существует очень большое поле для размышлений о природе вероятностных процессов, возможности предсказания будущего и роли в этом предсказании информации. Тут же проявляется необходимость возникновения (а возможно, извечного существования, в каждой структуре) специального механизма выбора (контроллера), существенно воздействующего на поведение структуры в следующий момент времени (о чем мы уже говорили) . Этот механизм можно считать также имеющим материальный носитель, а следовательно, обладающим своей собственной  волновой функцией – информационной волновой функцией или индивидуальной волновой функцией.

При этом функция  характеризует основные видимые состояния системы, общие для всех систем данного типа, а функция может характеризовать индивидуальные свойства именно данной системы. Это разделение существенно, но оно может меняться в зависимости от глубины рассмотрения задачи, и возможно различное разделение свойств системы на общие для данного класса систем и индивидуальные.

Однако, следует постулировать следующее положение, которое мы считаем бесспорным. Как только у системы взаимодействующих структур появляется свобода выбора того или иного результата события, моментально внутри нее возникает механизм осуществления этого выбора по какому либо принципу. Чаще всего такая возможность появляется у сложных многокомпонентных систем, открытых для взаимодействия с окружающим миром. Cистема может каким-либо внутренним образом, измерять векторную функцию  и даже изменять механизм ее действия, с целью обеспечения максимального сохранения  всей системы , а следовательно  .

Отсюда возникают определенные требования к изменению во времени вектора . Вектор  должен обладать очень большим количеством координат. Осмелимся высказать предположение , что в частном случае  может быть информационной структурой, изоморфной либо свободной группе, либо графу, которая в той или иной степени является отображением  во внутреннее пространство системы того или иного отрезка графа структур и событий самой системы и тех систем, которые взаимодействуют с нашей .

Сумма вероятностей всех возможных результатов события в данный момент должна быть по определению равной единице. Поэтому в каждый момент времени должно выполняться равенство


Это равенство представляет собой  так называемое  условие нормировки волнового вектора. Так как  - комплексный вектор с модулем равным 1,то, если мы имеем два вектора , для каждого события любой вектор  с модулем, равным единице, также может теоретически являться волновым вектором. Кроме того, если нам известна зависимость состояния от времени, которая  дается функцией  или функцией , то  любая их линейная комбинация тоже дает возможную зависимость вектора состояния от времени в процессе совершения события. . Это утверждение непосредственно распространяется на любое число возможных исходов данного события и справедливо для всех трех типов волновых векторов.

 

2. Мера, характеризующая совокупность взаимодействующих структур и соответствующий ей оператор.

 

Рассмотрим  некоторую меру , характеризующую систему в процессе происхождения события [1,9]. В общем случае в нижеследующих рассуждениях следовало бы говорить не об одной  мере, а о целом их наборе. Однако все рассуждения от этого по существу не меняются, тем более, что, исходя из синергетического принципа, для системы может быть выбрана какая-либо одна мера, характеризующая систему в целом. Поэтому в целях краткости и простоты мы говорим ниже всего лишь об одной мере. Значения , которые может принимать в результате свершения события эта мера для каждого результата события, будем называть ее собственными значениями, а об их совокупности будем говорить как о спектре собственных значений этой меры. В нашем случае величина  в рамках результатов данного события имеет дискретный спектр, и число значений этого спектра равно возможному числу исходов данного события. Собственные значения m  обозначим через . Обозначим далее единичный волновой вектор системы, соответствующий i-тому исходу события, которому соответствует i-тое собственное значение  через

 . Волновой вектор  может быть назван собственным вектором данного исхода события, а следовательно, собственным вектором значения . Каждый из этих векторов представляет собой n- мерный вектор с одной ненулевой комплексной координатой, модуль которой равен 1

 


В соответствии с принципом суперпозиции – линейностью векторного пространства, можно утверждать, что волновой вектор в любой момент времени во время события должен представлять собой линейную комбинацию тех собственных значений векторов , которые соответствуют определенным исходам события и соответственно собственным значениям меры m,.(если учитывать замечание, сделанное нами ранее, то в него можно включить также и состояние системы, которое она имела до совершения события.)

Поэтому в любой момент времени прохождения события волновой вектор может быть представлен в виде , где суммирование проводится по всем i, а некоторые коэффициенты. Таким образом, всякий волновой вектор может быть разложен по собственным векторам некоторой физической величины, принимающей некоторые конкретные собственные значения в результате реализации события. О системе векторов данного события, по которой может быть произведено такое разложение, говорят как о полной или замкнутой системе векторов.

Полученное разложение дает возможность определить вероятности реализации (то есть вероятности соответствующего результата при свершении события) у системы, имевшей в момент начала события вектор состояния того или иного из возможных результатов события, а следовательно, того или иного значения меры m из спектра, соответствующего данному событию. Действительно, эти вероятности должны быть билинейными по .

 Далее эти выражения, разумеется, должны быть положительными, наконец, вероятность реализации i- того значения меры должна обращаться в единицу, если результатом события становится состояние системы, соответствующее этому значению меры, то есть система приходит в состояние, соответствующее значению  и должна обращаться в нуль, если в разложении волнового вектора  отсутствует член, содержащий . Последнее означает, что искомая вероятность должна быть единицей, если равны нулю все коэффициенты, кроме только одного, модуль которого равен единице, и должно быть нулем, если данный коэффициент равен нулю. Сумма вероятностей всех возможных значений m должна быть единицей. Таким образом имеет место равенство


С другой стороны, умножив на  разложение и просуммировав по всем i , получим:


    Отсюда находим следующую формулу, определяющую коэффициенты разложения волнового вектора по собственным векторам

Если подставить сюда разложение вектора , то получим

Откуда видно, что собственные векторы должны удовлетворять условию [9]

 

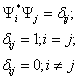
Таким образом, совокупность собственных векторов волнового вектора события образует полную систему нормированных  и взаимно ортогональных векторов, если каждый из возможных результатов события полностью определен.

    Введем понятие о среднем значении меры m, которая может быть получена в результате данного события.

Запишем это среднее значение меры в виде выражения, которое бы содержало  не коэффициенты, а сам вектор . Поскольку в выражение, стоящее в правой части, входит произведение ,то ясно, что искомое выражение должно быть билинейно по  и . Введем некоторый математический оператор, который мы обозначим как .  Пусть означает результат воздействия оператора на  вектор .

Определим теперь, по аналогии с квантовой механикой [9] оператор таким образом, чтобы

.

Легко видеть, что в общем виде он представляет собой некоторый матричный линейный оператор. Воспользовавшись выражением для i-того коэффициента, мы можем переписать определение среднего значения в виде .

Сравнивая два последних соотношения, видим, что результат воздействия оператора  на вектор  имеет вид

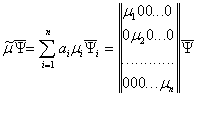
Таким образом, каждой возможной совокупности структур, которая возникает в результате свершения события, можно сопоставить меру, которой соответствует линейный оператор, представляющий собой диагональную матрицу, диагональ которой есть совокупность собственных значений меры, соответствующих различным исходам.

Если вектором  является один из собственных векторов, так что все коэффициенты, кроме одного, равны 0, то в результате воздействия на него оператора этот вектор просто умножается на соответствующее собственное значение . Таким образом, можно сказать, что собственный вектор данной меры является решением уравнения , где - постоянная, а собственные значения суть те значения этой постоянной, при которых написанное уравнение имеет решения, удовлетворяющие требуемым условиям.

Пусть m и n- меры совокупностей структур, возникающих в результате события, которые могут одновременно иметь определенные значения, а - их операторы. Собственные значения суммы  этих величин равны суммам собственных значений величин  m и n. Этой новой величине будет очевидно соответствовать оператор, равный сумме операторов . Действительно, если общие собственные векторы операторов ,то из  следует, что то есть собственные значения оператора равны суммам .

Наряду с суммой можно ввести понятие о произведении операторов как об операторе, собственные значения которого равны произведениям собственных значений величин  m и n. Легко видеть, что такой величине соответствует оператор , действие которого состоит в последовательном действии на функцию сначала одного, а затем другого оператора. Такой оператор изображается математически как произведение операторов . Действительно, если общие собственные функции операторов есть , то имеем:

 

 

(Символ обозначает оператор, действие которого на вектор  заключается в последовательном действии сначала оператора на вектор , а затем оператора на вектор .С тем же успехом мы могли бы взять вместо оператора  оператор ,отличающийся от первого порядком множителей. Очевидно, что результат воздействия обоих этих операторов на векторы будет одинаковым. Но поскольку всякий волновой вектор может быть представлен в виде линейной комбинации векторов , то отсюда следует, что одинаковым будет результат воздействия операторов и на произвольный вектор. Этот факт может быть записан в виде символического равенства

=или- =0. О таких двух операторах говорят как о коммутирующих друг с другом. Таким образом, мы подходим к важному результату, если две величины m и n могут иметь одновременно определенные значения, то их операторы коммутируют друг с другом. Может быть доказана и обратная теорема, если операторы коммутативны, то у них все собственные функции общие[9]. Частным случаем произведения операторов является оператор, возведенный в некоторую степень. На основании вышесказанного мы можем заключить, что собственные значения оператора  (p- целое число) равны собственным значениям оператора возведенным в ту же степень. 

 

8. Основное дифференциальное равенство для волнового вектора.

Оператор «действие -энтропия».

 

Пусть в какой-то момент времени t нам известен ве          ктор , который может быть представлен в виде.

 

.

 

В последнем соотношении мы приняли , что  -собственный вектор системы, соответствующий одному из возможных исходов события, равен какому-то комплексному числу с модулем равным единице, а вектор  единичный действительный вектор, отражающий направление, соответствующее i-тому собственному значению вектора . Вычислим производную от волнового вектора по времени.  Будем считать что размерность волнового вектора не изменяется. Это ограничение можно обойти следующим образом. Пусть во время события происходит изменение числа компонент вектора. Тогда можно с самого начала считать, что число компонент было больше на то число, на которое произошло изменение.

 

 

 

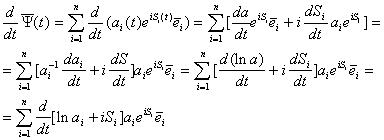
(В принципе можно рассматривать и более общий случай , когда меняются со временем и сами векторы , и в некоторых случаях, возможно придется так поступать, однако в нашем случае эту сложность можно обойти, предполагая, что мы находимся в рамках одного события и возможное изменение числа и типа векторов  мы рассматривать не будем)

Рассмотрим комплексный оператор, который назовем оператором «действие- энтропия»

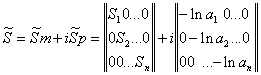.                                  (8.1)

 

 Тогда производная от волнового вектора по времени определится по формуле.

                                              (8.2)

Рассмотрим частный случай полученного тождества, соответствующий собственному вектору . В этом случае мнимая часть оператора «действие –энтропия»  становится сингулярной – все центральные члены матрицы, кроме одного, соответствующего собственному вектору события , стремятся к бесконечности, а этот единственный обращается в нуль. Однако, воздействие даже такого странного оператора на вектор сохраняет свой смысл – асимптотически результат воздействия оператора на  вектор дает нулевой вектор. Тем самым, в случае собственных векторов нашего события, мы можем в пределе пренебречь действием оператора «Энтропия» и сохранить лишь оператор «Действие».

Здесь зарыта очень глубокая проблема, которая связана с необратимостью события. Действительная часть введенного нами оператора существует в конечном виде лишь во время прохождения события. В связи с этим в процессе прохождения события мы всегда можем построить конечный оператор, обратный оператору «действие – энтропия», который позволяет нам теоретически обратить то или иное состояние. Однако, если мы уже пришли к какому-то результату, то действие оператора «Энтропия» прекращается сингулярным образом и он перестает оказывать влияние на процесс.. В этом вырожденном для оператора «энтропия» случае тождество (8.2)  принимает следующий вид

,                                              (8.3).

 а вместо оператора «Действие – Энтропия» можно  рассматривать лишь оператор «Действие» . Возвращение к рассмотрению этого оператора возможно лишь силовым образом. Однако, во все время прохождения события использование оператора  «Энтропия»- вполне корректно (вспомним фокусника с шариком) .

 

9. Действие и энтропия (информация) события.

 

Вычислим теперь средние значения действительной и мнимой частей оператора действия-энтропии.

.  (9.1)

Отсюда следуют два действительных равенства

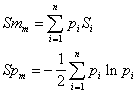                                             (9.2)

Особенно интересно для нас второе равенство (9.2) .

В современной науке широко используется скалярная величина, характеризующая свойства вектора . [14] - [21].  В учебниках и монографиях по статистической физике, термодинамике, теории вероятностей, теории информации и теории меры ее называют энтропией . Эта величина с  точностью до постоянного коэффициента совпадает с В дальнейшем будем называть число  энтропией события. В работе [21] А. М. Хазеном было указано на связь между энтропией и механическим действием а также введен термин: действие-энтропия-информация, который мы и используем в настоящей работе.    

Рассмотрим более подробно.

Попытаемся построить многообразия . Уравнения этих многообразий размерности  имеют вид:

.

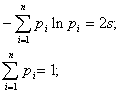Определим точки, в которых энтропия равна нулю. Таких точек .

 

Теперь найдем точку, в которой  максимально. .

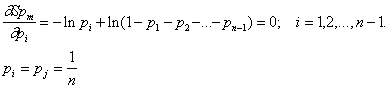
Тогда величина энтропии

То есть в случае, когда все исходы события равновероятны, энтропия системы перед событием по отношению к результату события увеличивается пропорционально логарифму числа возможных вариантов исходов события. Чем ближе вектор  к одному из ортов n -мерного пространства, тем ближе энтропия системы в момент, предшествующий событию, к нулю. Энтропия вероятности события в момент после его совершения оказалась равной нулю. То есть свершение события обнуляет энтропию будущего этого события.

Обозначим энтропию будущего для события до его свершения через   Энтропию системы взаимодействующих структур после события обозначим через . Приращение (уменьшение) энтропии в результате того, что событие произошло, обозначим через . Тогда получаем простое соотношение

= -                                                 (9.3)

Свершение события изменило (уменьшило) энтропию будущего.

Так как в результате события  оказалось равным нулю, то из соотношения (9.3) получим

=-                                                   (9.4)

Введем новое понятие - информация, приобретенная в процессе выполнения события , и определим ее как величину, противоположную убыванию энтропии

                                               (9.5)

Из соотношения (9.4) следует, что 

                                                (9.6)

или

                                              (9.7)

Разность информации, приобретенной в результате события, и энтропии будущего, в момент перед началом события, равна нулю.

Или

Информация, приобретенная в результате события, равна энтропии будущего в момент перед началом события.

Закон (9.7) может быть назван законом сохранения информации-энтропии будущего для события.

Хотя в нашей интерпретации он кажется абсолютно тривиальным, однако, возможно, его тривиальность эквивалентна тривиальности второго закона Ньютона, так как представления об энтропии и информации очень разнообразны и идут из разных теорий. Если левую и правую части можно будет отождествить с разными величинами, то смысл этого закона возрастет многократно.

Попытаемся построить многообразия .

Как выглядят кривые  вблизи особых точек?

Рассмотрим частные случаи.

 

 

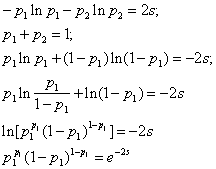
Найдем точки , в которых энтропия равна нулю.

 

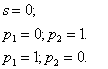
Других точек нет.

Найдем точки , в которой энтропия имеет экстремум

 

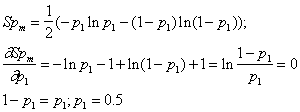
Энтропия максимальна при и равна

Предположим, что

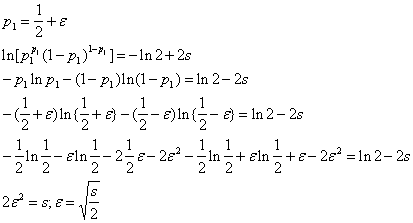
Уменьшение энтропии приводит к увеличению неоднородности в распределении вероятностей, пропорциональной корню квадратному из уменьшения энтропии. И наоборот изменение неоднородности распределения вероятностей относительно равномерного приводит вблизи точки максимума энтропии к ее уменьшению, пропорциональному квадрату величины неоднородности – как и следовало ожидать, вблизи гладкого максимума мы имеем параболическую кривую зависимости энтропии от вероятности.

((Более подробное исследование энтропии выполнено в Приложении 5).

 

Этюд 31.

 

Волновой вектор-матрица события.

 

1. Волновой вектор–матрица системы взаимодействующих структур.

 

Вернемся к более подробному рассмотрению графа взаимодействия структур и систем. Предположим, сначала, что каждый возможный вариант исхода события состоит из определенной совокупности не взаимодействующих в данный момент структур. Тогда для каждого действия  каждого варианта результата i- того события величина действия всей системы  может быть представлена в виде суммы действий структур, входящих в систему.

 

 

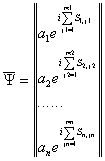
    Однако, такая простая запись нас не должна устраивать, так как в ней не отражено главное свойство структур – их существование и независимость. Поэтому я предлагаю иную запись, по моему мнению, значительно более адекватную дуальной сущности графа структур  и событий. А именно, приведем в соответствие системе, состоящей из одновременно существующих детерминированных структур, некоторую диагональную матрицу, диагональные элементы которой будут представлять  мнимые числа с модулем, равным единице.

 

 

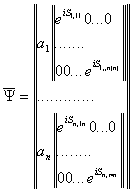
    Полученная алгебраическая структура представляет собой простейший случай вводимого нами понятия комплексный вектор-матрица состояния системы, являющегося сечением по конкретному значению времени для графа структур - событий. Главными элементами вектора-матрицы являются вероятностный комплексный вектор, сумма квадратов модулей которого равна единице и комплексная диагональная матрица, каждый диагональный член которой представляет собой комплексное число с модулем, равным единице.

Эти основные элементы в зависимости от сложности описываемой системы могут комбинироваться между собой в различных сочетаниях. Кроме того, ввиду того , что мы имеем дело с открытыми системами, предлагаемый нами вектор–матрица может быть вместе с исследуемой системой расширен за счет включения в систему новых элементов из окружающей среды.

При этом в случае детерминированного включения мы можем построить новую расширенную матрицу, в случае же вероятностного включения – строится новый расширенный вектор.

Аналогично возможно неограниченное расширение вектора- матрицы вглубь - каждый ее элемент может быть вновь, на более глубоком уровне развернут в виде вектора или матрицы в зависимости от его физической сущности. И этот процесс, во всяком случае, теоретически, может быть продолжен в обе стороны. (Здесь стоит подумать о некоем алгоритме для ЭВМ, так как это очень похоже на иерархическое построение баз данных или баз знаний - вообще здесь широкое поле деятельности для алгоритмирования, однако это значительно глубже, так как здесь мы имеем дело с комплексными величинами, а также так как здесь учтена бифуркационная  компонента графа структур - событий ).

Таким образом, мы предполагаем математически описать  проекции событийного графа как минимум, на четыре координаты:

1)   временную (вводимая нами вектор-матрица является достаточно сложной функцией от времени и во время событий происходит не только количественное, но и качественное изменение ее структуры.)

2)   бифуркационную (эта координата отражается в параметрах действительных частей вектора.)

3)   проекцию действия - проекцию меры (эта координата отражается в детерминированном случае в матрице действия, диагональные члены которой представляют собой комплексные числа с модулями, равными единице, и аргументами, определяемыми действием);

4)   четвертая проекция нашего графа - масштабная (иерархическая) – мы можем расширять иерархии систем и структур как включая в нее новые структуры и системы, так и вскрывая все более глубокую сущность подсистем и элементов, входящих в изучаемую нами систему. Здесь наиболее ярко отражается иерархическая сущность природы –ее важнейшая – масштабно- иерархическая координата.

Мы не коснулись пока еще одного параметра порядка графа структур и событий  – классификационного – системы, структуры и события могут быть при одном  и том же действии принципиально разными по каким либо другим параметрам, при этом их различия могут быть континуальными, то есть зависящими не от дискретных, а от континуальных параметров, что приводит к необходимости изучения волновых свойств систем и структур. Однако, эта тема требует специальной дополнительной проработки на следующем уровне рассмотрения.

Вернемся к введенному  нами вектору - матрице и рассмотрим некоторые свойства этой конструкции, соотнося их с физической моделью, которую мы положили в основу нашего рассмотрения.

Возникает вопрос об обратном переходе от формы представления в виде вектора-матрицы к свернутому по матрицам представлению в виде волнового вектора.

Этот переход в рассматриваемом нами частном случае достаточно прост. Необходимо вычислить определитель каждой из матриц и заменить каждую из них ее определителем.

Физически это эквивалентно тому процессу, когда мы имеем систему из нескольких независимых структур, каждая из которых обладает некоторым действием, и мы хотим рассматривать их в совокупности, приписав новой системе некоторое действие, которое естественно положить равным сумме действий структур, в нее включенных. Таким образом, переход от одной формы записи вектора-матрицы к другой в нашем частном случае осуществляется «исследователем» в зависимости от того, на каком иерархическом уровне рассмотрения он находится.[21]. Естественно,  рассмотренный простейший вариант построения вектора -матрицы  справедлив лишь в том случае, если исследуемая нами система состоит из четко различимых между собой структур.

В случае же так называемых «целостных» структур и систем, когда четкое разделение на отдельные структуры невозможно, хотя частичное разделение присутствует, существует какая-то непонятная пока часть системы, в каком-то смысле объединяющая все входящие в нее подструктуры, но не входящая полностью ни в одну из них. Пусть в этом случае эта общая для всех подструктур часть имеет действие, равное . Предложенная нами вектор - матрица может быть модифицирована и для этого варианта, в котором она примет вид .

 

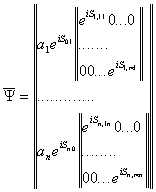
Это очень похоже на рассмотрение формирования молекулы из нескольких атомов, при этом роль общего для структуры элемента играет общий для двух атомов электрон. В нашем построении рассматривается значительно более общая ситуация: роль общего для всех подструктур элемента может играть, например, кровеносная система  человеческого организма. Здесь, конечно, нет четкости, т.к. подобная структура может, по-видимому, формироваться лишь при наличии процессов непрерывного взаимодействия, что требует в дальнейшем более глубокого рассмотрения. 

Тем самым, введенный нами вектор-матрица  может обладать возможностями модификации в соответствии с изменением реальных объектов, им описываемых. Рассмотрим еще один путь его модификации. Рассмотрение начнем вести с последней формы вектор-матрицы. Предположим, что одна из подструктур   может иметь несколько модификаций , с различными значениями действия, вероятность появления каждой из которых определена соответствующей проекцией вектора .В этом случае наша конструкция модифицируется следующим образом.

 

 

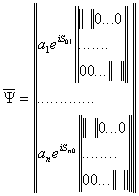
Здесь  внутри каждой матрицы вновь строятся векторы-матрицы аналогичной формы 

Подумаем о возможных вариантах свертки локального комплексного вектора, построенного нами внутри вектора-матрицы. Это должно быть некое усреднение, которое в результате должно привести нас к замене комплексного вектора некой комплексной скалярной величиной. Рассмотрим отдельно один из векторов, который мы предполагаем свернуть. Этот вектор нам уже знаком - это волновой вектор бифуркационного события.


                                                           

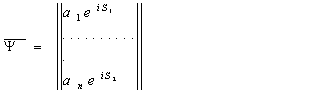
 Ему соответствует оператор “действие – энтропия” следущего вида.


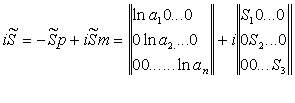
 Примем в качестве свертки вектора  экспоненту среднего значения этого оператора. Итак, сверткой произвольного вероятностного вектора внутри введенного нами вектора-матрицы может служить комплексная величина:

 


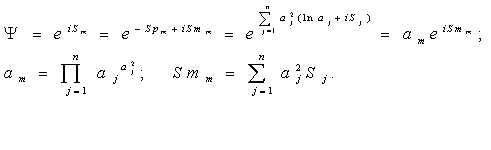
Таким образом, в матричных составляющих построенного нами вектора-матрицы за счет свертки внутреннего вероятностного вектора появляется модуль, отличный от единицы. Физически логарифм этой величины характеризует энтропию системы, соответствующей  данному вероятностному вектору. Аргумент этого комплексного числа соответствует осредненному действию системы. Энтропия элементов матрицы суммируется при свертывании матрицы в скаляр путем взятия её определителя.

При переходе же с одного уровня на другой включение внутренней энтропии во внешнюю происходит значительно более сложным образом, что мы и попытаемся показать ниже. Кстати, аналогичное утверждение можно будет сделать и относительно действия.

Эти новые формулы позволяют путем свертки переходить с одного уровня иерархии на другой.


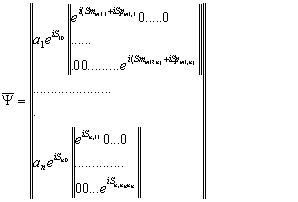
    Сначала свернем векторы, входящие во внутренние матрицы при помощи процедуры вычисления средних значений оператора энтропии этого вектора

 

Уже здесь мы сталкиваемся с принципиально новым явлением. Красивый вектор-матрица, у которого существенно разделены модули и аргументы всех его элементов, на этапе свертки приобрел комплексные показатели степени, выделение действительной части которых из показателя нарушает всю стройную картину.

 Здесь есть два выхода – либо отказаться от этой заманчивой перспективы, либо, считая верным выбранный нами путь, попытаться дать ей объяснение, введя новые понятия, и попытаться придать ей корректность, показав ее правильность в тех частных случаях, когда стандартная процедура работает. Именно по последнему пути мы и попытаемся пойти.   

Свернем при помощи взятия определителя внутренние матрицы в свернутом в первый раз векторе - матрице. Эту процедуру мы  выполняем по аналогии с тем , что мы делали раньше для детерминированных независимых структур. Ранее мы считали, что все структуры, входящие в систему, определенную нашим вектор-матрицей, во первых, независимы, а во вторых, детерминированы, и, исходя из этих соображений, ввели саму матрицу и операцию взятия определителя, соответствующую ее свертке. Сейчас сохранилось условие независимости (или мы частично учли отклонение от него, вынеся за скобку комплексный множитель). Однако, каждая отдельная структура уже четко не определена, о чем говорит появление действительной части в показателе степени. Эта действительная часть уже имеет не тот физический смысл, что амплитуда векторной функции, введенной нами ранее. Вынесение ее из показательной функции не даст нам никакого нового физического смысла., так как эта величина не войдет ни в какой вектор, модуль которого равен 1.

Поэтому интереснее оставить ее в виде мнимой части локального значения действия- энтропии данной подсистемы. Указанная величина может интерпретироваться как мнимая часть комплексного действия энтропии- той структуры, которая в данный момент не определена, а находится в процессе становления, хотя этот процесс происходит независимо от других структур, входящих в нашу систему.


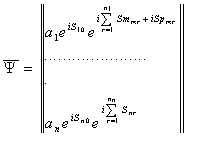
Такой подход, являясь значительным обобщением предыдущего, во всяком случае, позволяет более уверенно идти по намеченному нами пути. Итак, забыв о комплексности показателя степени, применим к матрицам, входящим в частично свернутый вектор- матрицу, операцию взятия определителя и произведем еще одну свертку. Тем самым, мы вычислим суммарное действие и суммарную энтропию каждой матрицы, соответствующей данной совокупности структур.      

 

И вновь мы получили нестандартный результат. – аргумент экспоненты нашего вектора содержит компоненту, которая может изменить действительную часть (и существенно), но тогда теряется физический смысл нашего рассмотрения. Поэтому простое вынесение действительной части из экспоненциального представления нецелесообразно и каким-то образом должно быть математически запрещено, так же как и внесение в матрицу, соответствующую независимым подструктурам комплексного члена, описывающего свойства, общие для всей структуры. Над этим стоит специально подумать - вообще получается совершенно новый для  автора, а  возможно , и для математики объект, для которого должны быть установлены свои законы.

Итак продолжим. После того, как свертка внутренних матриц закончена, уже можно умножать на общий комплексный множитель. В результате получаем почти классический волновой вектор, соответствующий данному событию.

 

 

 

 

 


 

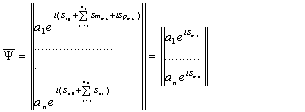
В последней формуле введены следующие обозначения.

Эта величина характеризует комплексные значения «действия энтропии» для частных векторов – матриц.

Этот последний волновой вектор вновь необычен. Ведь если действовать по стандарту, то его нужно преобразовать, выделив из экспоненциальной части действительный модуль. Однако тогда нарушатся все основные физические принципы, которые легли в основу наших построений. А это значит, разрушатся и сами построения. Отсюда следует вывод, что так делать нельзя. Значит, существует существенное различие между внешними вероятностными членами нашего вектора и внутренними энтропийными членами. Это очень интересный вывод.

Энтропия складывается только у независимых структур или систем одного ранга. Если же мы имеем сложную структуру, то ее энтропия также зависит от энтропии входящих в нее подструктур, но несколько более сложным образом, закономерность которого мы сейчас опишем.

Вектор - матрица на каждом уровне иерархии может быть представлен в виде произведения некоего вектора-матрицы на действительный волновой вектор единичной длины , с координатами, соответствующими вероятностям реализации в результате события той или иной составляющей этого вектора. Если каждый из указанных векторов-матриц удастся свернуть по тому же принципу, то мы получаем новый вектор. Однако осреднение следует делать только по вероятностному волновому вектору наивысшего ранга.

В этом случае получаем следующую формулу для полной энтропии- действия

Разделяя действительную и мнимую части, получаем общую формулу для вычисления компонент действия-энтропии волнового вектора-матрицы. 

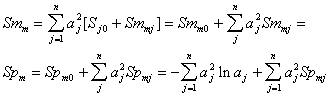
Из полученных, на наш взгляд, совершенно новых формул можно сделать очень интересные выводы.

Комплексное число «действие- энтропия» события, происходящего с иерархической системой, может быть представлена в виде суммы собственно комплексного «действия-энтропии», определяемого внешними значениями вероятностей и общего для всей системы действия, и перекрестным комплексным «действием-энтропией», осредненным по амплитудам вероятности внешней части структуры комплексных энтропий-действий для различных вариантов исходов события.

Особенно интересна полученная формула для энтропийной части нашего комплексного числа.

Очень красивая формула, содержащая в себе глубокий смысл.

Фактически она включает целую иерархию вложенных друг в друга формул одного и  того же типа, которая, в принципе может быть расширена наружу и продолжена внутрь. Эта иерархичность сродни  иерархичности живых биологических структур. При этом может быть предложен очень интересный механизм минимизации «действия –энтропии» именно в рамках иерархических структур.

Этот механизм состоит в сочетании фрактальности – то есть масштабного подобия систем и подсистем, осуществляемого за счет какого- либо резонансного механизма, и локального введения неоднородности в один из элементов иерархии – в принудительном порядке – например, увеличение локальной амплитуды вероятности того или иного варианта реализации события на одном из уровней иерархии . Тогда за счет резонансного механизма этот процесс пройдет по всем иерархическим уровням, что позволит существенно уменьшить -действие - энтропию системы, практически не меняя ее структуры.

Вернемся к полученному нами вектору матрице и попробуем записать его в несколько ином, более компактном виде.

Вектор – матрица представляет собой некую иерархию из вложенных друг в друга вероятностных векторов и матриц действия. Эта иерархия в первом приближении может быть представлена в форме.


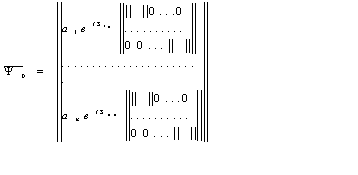
В выписанной структуре внутри между двойными вертикальными чертами вновь стоят вектор-матрицы с аналогичной структурой. Попытаемся записать полученное соотношение в символьном виде.

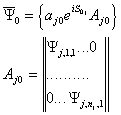
Здесь каждая вложенная  вектор- матрица, которая  может быть нами обозначена через  вновь имеет вид

 

Этот процесс может быть продолжен неограниченно до тех пор, пока в системе можно будет различать подсистемы все более низкого уровня иерархии.

 

Этот же процесс можно начать и продолжать и вверх, рассматривая более высокие ступени иерархии, в которые входит анализируемая нами система, состоящая из взаимодействующих структур. Процесс расширения может быть осуществлен следующим образом. Предположим, что вектор  включается в качестве, например, первого элемента в некоторую матрицу

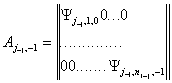
где сама матрица является элементом нового вектора

И  так неограниченно вверх по уровням иерархии.

Тем самым, мы обнаружили еще одно очень интересное свойство нашего вектора-матрицы – возможность практически неограниченного расширения его как вглубь – до самых мелких подструктур, так и наружу, путем включения в него  все более высоких уровней иерархии. При этом, как было показано выше, остановка может быть сделана на любом уровне движения вглубь. Необходимо только свернуть по вышеуказанным правилам все остальные, не рассматриваемые нами глубинные уровни иерархии и заменить их соответствующими значениями действия и энтропии. В принципе, по-видимому, возможно нечто аналогичное выдумать и для внешних уровней иерархии.

 

 

 

                                           

 

 

 

 

                                                      

                              Обобщенное равенство Шредингера

 

Так как введенная нами вектор-матрица является сечением мирового графа по времени, то все входящие в нее элементы являются функциями времени. Как нами было указано ранее, всегда можно считать, что зависимость вектор-матрицы от времени гладкая везде, за исключением, возможно, некоторых особых точек. Если это не так, то легко могут быть введены обобщенные функции и обобщенные производные и математическая строгость от этого не нарушится.

Следовательно, мы можем сформировать производную от вектор-матрицы.

 

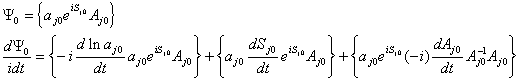
Введем следующий оператор над вектор - матрицей

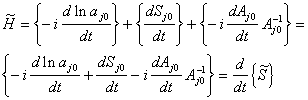
Тогда получаем обобщенное равенство Шредингера для введенной нами вектор-матрицы.

 

 

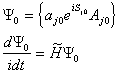
Можно ввести обозначение.

 

Тогда

И оператор действия-энтропии будет иметь вид:

В последнем соотношении введено новое определение, согласующееся с известным определением экспоненты линейного оператора.

Обобщенное равенство Шредингера для введенной нами вектор-матрицы имеет вид

 

Таким образом, оператор действия- энтропии представляет собой с точностью до коэффициента, равного мнимой единице операторный логарифм от вектор - матрицы  , характеризующей текущее состояние сечения графа структур и событий для той или иной совокупности структур.

Прежде, чем завершить этот параграф, остановимся на построении оператора как иерархической цепочки операторов, соответствующих введенной нами вектор - матрице. Для этого раскроем на следующем шаге иерархии реальный смысл величины.

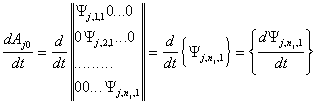
Подставляя полученное выражение в формулу для производной от вектор - матрицы по времени, получим

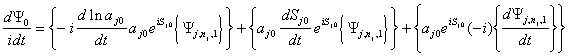Ввиду того, что матрица  диагональная, можно последнее равенство записать в виде

Получившееся равенство может быть записано в операторном виде

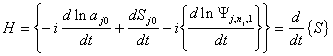
Последние формулы позволяют выразить производную по времени от вектор - матрицы через ее непосредственные характеристи

..На данном уровне рассмотрения а также через аналогичные производные от составляющих вектор-матрицы на следующем , более глубоком уровне рассмотрения. Тем самым найдена рекуррентная связь между двумя соседними уровнями иерархии структуры вектора- матрицы. Полученная связь методом математической индукции может быть продолжена вглубь иерархии вектор- матрицы. Аналогичное продолжение путем инверсии и включения новых элементов может быть осуществлено вверх по иерархической лестнице.

 

 

 

.Частные случаи вектор - матрицы.

 

Рассмотрение любой вектор - матрицы путем свертки может быть сведено к рассмотрению волнового вектора, у которого, однако, показатель экспоненты, в отличие от чистого рассмотрения, будет комплексным, что само по себе очень интересно.

Рассмотрим некоторые частные случаи.

Пусть мы имеем простейший частный случай детерминированной системы

 

Простейшим случаем является случай постоянного значения действия . Физически этот случай соответствует какой-то системе, которая ни с кем или ни с чем не взаимодействует, имея какое-то не зависящее от времени состояние. Нет ни времени, ничего. Это какая-то монада , про которую ничего и сказать то нельзя. В принципе даже на первых порах , до взаимодействия, и не важно, какова сама величина . Хотя в дальнейшем , при взаимодействии таких монад относительная величина  для каждой из них, по-видимому, будет играть соответствующую роль. Обобщенное уравнение Шредингера в этом случае будет иметь вид:

  

Оператор Гамильтона - Колмогорова в этом случае есть оператор обнуления волнового вектора. Система не имеет никакой энергии. Оператор действия – константа, равная . Единственная интересная особенность этого нашего первого рассмотрения – это появление квантования величины . Если мы каким-либо образом условимся , что наблюдатель может обнаружить структуру только в том случае, если вектор-матрица окажется равной действительному числу, то мы получим естественное квантование величины действия . Вектор-матрица оказывается равной действительной величине лишь в том случае, если  . Таким образом, мы можем наблюдать структуру лишь с дискретными значениями действия , отличающимися друг от друга на величину , при этом все остальные значения действия , хотя и существуют, в нашем реальном мире нам недоступны. Здесь может быть развита любая философия, но дело не в ней. Введение в рассмотрение комплексной волновой вектор - матрицы приводит к естественному квантованию действия в реальном мире на первом же наиболее глубоком уровне рассмотрения. Это очень интересно и поучительно. Квантование связано лишь с комплексностью вектор - матрицы . Комплексность окружающего нас мира – может быть самый глубокий постулат любой теории, которая желает этот мир описать! Из комплексности при попытке выйти в реальный мир автоматически следует квантовость действия , даже на таком уровне, когда ни время, ни пространство еще не введены. От нашего рассмотрения легко перейти и к обычному квантовому рассмотрению. Пусть в реальной природе мы не знаем истинного масштаба действия как безразмерной величины, являющейся реальной частью энтропии-информации - действия. В этом случае между нашим действием  и измеряемым в природе действием  должен существовать масштабный переход , который может быть записан в виде  В этом случае реально анализируемые значения действия могут наблюдаться лишь в виде дискретных значений . Тем самым мы пришли к одной из возможных форм обоснования  квантовости мира на основе предположения о комплексности волновой вектор-матрицы, характеризующей систему.

Здесь необходимо отметить, что рассматриваемый нами случай относится в действительности, к системе, которой как бы нет, про которую мы ничего не знаем, к «монаде», полностью скрытой от нас. В этом случае никакой динамики не существует ни снаружи, ни изнутри. Да и самое значение действия  не столь уж важно. Да и все наши рассуждения о квантовании ничего другого , кроме некоторых намеков на умозаключения пока не содержат.

Перейдем теперь к рассмотрению более общего случая, когда система, как и прежде, детерминирована в комплексной области, но волновой вектор (частный случай волновой вектор-матрицы) , является некоторой функцией от времени. В этом случае общее представление для волнового вектора имеет вид     

Модуль волнового одномерного вектора равен 1, значит существование системы взаимодействующих структур однозначно определено. Однако эта система каким-то образом меняется во времени . Это изменение может быть представлено в виде какой-то аналитической зависимости. А именно  

Ряд Тейлора для функции действия.

Тогда обобщенное дифференциальное уравнение Шредингера  примет вид .

,

 а в момент времени, равный  примет вид ,

 

Необходимо отметить здесь очень интересный момент . В принципе, наше рассмотрение является очень общим. Ведь мы рассматриваем любую детерминированную якобы замкнутую систему. И вот тут возникает очень интересный вопрос – вопрос о транслируемости во времени. Очень интересно. Является ли в нашем детерминированном случае обобщенное уравнение Шредингера инвариантным во времени или нет. Если нет, то изменение начала отсчета по времени приводит к изменению самого уравнения Шредингера. Если да, то мы получаем принципипально новый закон сохранения – а именно .

Если в замкнутой детерминированной системе ее интегральное поведение описывается уравнением Шредингера , инвариантным относительно изменения точки отсчета времени, то величина  производной от действия системы по времени  такой системы оказывается постоянной, не зависящей от времени величиной. Все остальные производные от действия по времени оказываются равными нулю.

Тем самым из условия инвариантности уравнения Шредингера по времени мы автоматически получаем обобщенный закон сохранения энергии для замкнутой детерминированной системы.

Таким образом, введенное нами дополнительное допущение об инвариантности уравнения Шредингера по времени привело нас к допущению о сохранении полной энергии замкнутой системы. Если предположить обратное, то энергия системы меняется, система с кем-то или с чем-то взаимодействует и энергия не сохраняется.

Здесь необходимо отметить еще один очень важный аспект.

Если случай с постоянным значением действия соответствует стационарной точке некоей динамической системы, то случай с постоянным значением энергии соответствует, по-видимому, аттрактору в виде цикла, то есть все элементарные частицы , имеющие энергию представляют собой аттракторы динамических систем, по одной из координат которых существует циклическое перемещение, частота которого определяет энергию системы.

Это все хорошо для изолированных структур.

Так как здесь вся энергия системы определяется производной от действия по времени. В случае взаимодействия системы с другими системами возникают сложности , которые мне пока совершенно непонятны. Можно мыслить себе как внешнюю энергию взаимодействия – то, что мы называем потенциальной энергией, так и внутреннюю энергию самой структуры, характеризующей ее собственное состояние . Но откуда они берутся и как они между собою соотносятся пока абсолютно непонятно. Проблема разделения производной от действия на две части и перехода к анализу лагранжиана и гамильтониана системы пока совершенно непонятна. В классической и квантовой механике это вводится в качестве постулата, который, в частности выглядит в виде второго закона Ньютона ( из него то все и вытекает). Но в нашем рассмотрении хотелось бы более глубоких обоснований. Фактически, хотелось бы обоснования природы сил, действующих на взаимодействующие структуры. Я думаю, что к этой проблеме мы будем многократно возвращаться на новом уровне.  

Попробуем обобщить сделанный нами вывод на более общий случай.

В более общем случае, как мы это видели ранее, любая замкнутая система структур может быть описана одним комплексным числом, являющимся сверткой оператора энтропии-информации системы. При таком описании волновая вектор-матрица представляет собой комплексное число .Здесь - энтропия-информация системы- действие системы. В отношении действия и его производной по времени для замкнутых квазистационарных систем мы уже сказали выше то, что было необходимо. Попытаемся проанализировать аналогичным образом недетерминированную систему. Какими свойствами должна обладать волновая функция от времени, чтобы система оставалась стационарной или квазистационарной в том случае, если в ее волновой функции присутствуют члены , изменяющие амплитуду.

Рассмотрим первоначально случай, когда энтропия системы не зависит от времени. В этом случае  . Физически это может означать следующее. Часть структур, входящих в систему, не детерминированы и находятся в состоянии незавершенного события, откуда они могут попасть в какое-либо состояние , на не хотят делать этого. В принципе, в таком состоянии находится будущее любой недетерминированной системы. Поэтому вычисленная в данный момент волновая функция будущего системы имеет постоянное значение, если все возможные события уже произошли и далее идет повторение тех же результатов. Этот вариант очень интересно рассмотреть более подробно. Его анализ может дать нам очень интересную новую информацию о связи энтропии будущего и энтропии настоящего.

Здесь интересной является проблема, может ли система в течение долгого времени оставаться в состоянии неопределенности, когда ее энтропия конечна и постоянна. Это достаточно глубокая философская проблема. По-видимому, она может иметь несколько ответов.

Первый ответ.

Пусть система имеет n стационарных точек и до совершения события находилась в одной из них , и эта точка была устойчивой.(в нашей интерпретации система имела постоянное значение действия.

Изменение времени привело к некоторому изменению параметров системы - такому  что стационарная точка стала сначала нейтральной , а затем неустойчивой. При этом произошло такое изменение фазового пространства системы, что в зависимости от того, какой минимальный внешний импульс дается точке фазового пространства она может попасть в любую из притягивающих точек.

При этом, однако, она может очень долго находиться на границе аттракторов и никуда не скатываться. В этом случае событие может затянуться во времени и его энтропия , вырастя от нуля до конечной величины определяемой числом притягивающих стационарных точек, в течение некоторого времени оставаться либо постоянной, либо меняться в некоторых пределах. Осредняя ее по времени , мы получим среднюю энтропию события. Здесь можно, более подробно рассмотрев динамику, даже вычислить вероятности перехода к другим аттракторам а следовательно энтропию. Если аттракторы, к которым может выйти система , определены , а также не меняются сепаратрисы, отделяющие бассейны притяжения этих аттракторов, то энтропия системы, находящейся в переходной зоне в среднем, может считаться постоянной в течение всего периода происхождения события.        

. А пока наметим некоторые наброски новых проблем. Во первых ситуация с постоянной энтропией - информацией может наблюдаться и при реальных процессах. Назовем их затянувшимися событиями. Здесь можно вспомнить топологическую аналогию. Пусть какое-либо состояние системы из устойчивого превратилось в неустойчивое, из которого система может с определенной степенью вероятности перейти в любое из других устойчивых состояний. В этом случае образуется некоторая энтропия-информация. Однако она почему-то задержалась вблизи этого состояния и не хочет переходить ни в одно из предписанных ей. Это может продолжаться сколь угодно долго. В этом случае энтропия-информация настоящего также окажется постоянной.

Воможна и другая модификация того же варианта ,связанная с тем . что стационарная точка , соответствующая состоянию системы до начала события в действительности является не стационарной точкой а неким аттрактором более сложного вида, область действия которого концентрируется вблизи стационарной точки. В этом случае возможен непредсказуемый заранее выход на границу области притяжения этого аттрактора в любой его точке. И далее, как и выше.

Может быть еще один интересный вариант. Пусть состоянию системы до события соответствовал некоторый цикл  ( об этом мы уже говорили несколько ранее). цикл удвоился, то есть система имет уже две частоты колебаний . отличающиеся в два раза. То есть система как бы вступила в пору неопределенности. Она мечется между двумя возможными состояниями. Хотя в каждый конкретный момент времени состояние определено, в среднем, за некоторый малый промежуток времени состояние системы может быть представлено в виде совокупности нескольких чистых состояний с определенными коэффициентами, а эти коффициенты и есть наши вероятности. Тем самым, система, оказавшаяся включенной в систему циклов, может рассматриваться как недетерминированная система, соответствующая  возможности выбора того или иного цикла или того или иного стационарного состояния. Так как мы уже знаем, что  в некоторых случаях изменение параметра (например, времени) приводит к гиперболическому росту бифуркаций и даже к переходу к странному аттрактору, то в этом случае в процессе события или в процессе непрерывно совершающихся событий происходит рост энтропии вплоть до бесконечности в случае перехода к странному аттрактору.

Аналогичная картина может наблюдаться и при другом сценарии, когда бифуркации приводят к динамике систем на торе или сфере n-ной размерности а в дальнейшем к тому же хаосу. И здесь возможно формирование недетерминированной системы, соответствующей длительно продолжающемуся событию.

Выход из такого состояния в более не менее детерминированную структуру приводит к уменьшению энтропии и поступлению информации.

При этом система из эргодического состояния, соответствующего той или иной динамической системе выходит на более детерминированный участок, приобретая некоторое действие и информацию извне.  Если в процессе события энтропия сохраняется постоянной, то ее на более высоком уровне вновь можно обнулить, и считать наше затянувшееся событие почти детерминированным событием со средним значением действия или энергии. Итак, осреднение по времени и интегрирование по иерархиям позволяет превращать в рамках нашего рассмотрения недетерминированные процессы в детерминированные и затянувшиеся события в квазистационарные состояния.

В принципе, нам пока не важно, каким реальным способом будет поддерживаться постоянное не равное 0 значение энтропии- информации системы. Важно другое, что если это каким-либо образом осуществляется, то уравнение Шредингера для комплексной полностью свернутой вектор-матрицы системы практически совпадает с полностью детерминированной системой.

 .

Из этого следует некоторый очень общий и очень интересный вывод. Любая замкнутая недетерминированная система, имеющая постоянное значение энтропии- информации должна вести себя в интегральном смысле как детерминированная система. Этот вывод очень интересен. Например, построение практически детерминированной динамики сплошной среды для макроскопических объектов стало, по-видимому, возможным благодаря тому, что внутренняя энтропия этих сложных систем , являющихся локально равновесными, достигла своего максимума и остается близкой к максимальной в процессе динамики макроскопических объектов. Тем самым мы получаем еще один пример, когда энтропия- информация постоянна, и не только постоянна, но и близка к максимуму для данной системы. Хотя мы пока не касаемся этого наиболее важного практического случая, однако, общие соображения тоже весьма интересны.

Пойдем несколько далее. Попытаемся пойти по тому же пути, по которому мы шли ранее. А именно, разложим величину  в ряд Тейлора, как это было сделано ранее для величины действия.

 

В этом случае обобщенное уравнение Шредингера примет вид

Это справедливо вблизи точки . Чтобы это уравнение было инвариантно относительно трансляции времени, необходимо чтобы величина  равнялась постоянной величине, не зависящей от времени. То есть постоянной величиной должна быть комплексная величина свертки оператора Гамильтона- Колмогорова. Что это значит физически? Ну если  =0, мы возвращаемся к предыдущему случаю. Если , то с увеличением времени энтропия- информация системы неуклонно возрастает по линейному закону. Одновременно по экспоненциальному закону стремится к нулю модуль волновой функции системы при сохранении её энергии. Волновая функция системы не является в этом случае даже в среднем, не изменяющейся во времени функцией. Состояние нельзя считать стационарным. Несколько по –другому, но еще более парадоксальным оказывается случай .В этом случае в какой-то момент величина   становится равной нулю и условия инвариантности нарушаются. Кстати, то же самое происходит и в случае отрицательной энергии.

Пока нам не ясно, каким физическим явлениям эти вещи соответствуют.

Но можно вновь пофантазировать.

Рассмотрим первоначально первый случай, когда скорость роста энтропии положительна. Если мы предположим, что при этом сохраняется действие ( или энергия) , то это может соответствовать , например. следующему физическому случаю. Пусть первоначально мы имели одну структуру , которая может либо размножиться на две, либо остаться такой , какая она есть. Проанализируем сначала вектор состояния такой структуры будущего.

Предположим первоначально, что структура в некоторый момент может либо разделиться на две , либо не разделиться на две  и вероятность каждого исхода такого такого события равна 0.5  В этом случае энтропия будущего равна  ln2. Предположим далее, что событие произошло и после этого каждая структура вновь может разделиться с вероятностью 0.5 .  Тогда с вероятностью 0.25  мы будем иметь вариант 1 структуры, с вероятностью 0.25 –две структуры , появившиеся из первой структуры на втором этапе. С вероятностью 0.125 – две стрктуры, появившиеся на первом этапе, с вероятностью 0.125 – три структуры, появившиеся из одной из разделенных структур, с вероятностью 0.125 три структуры , появившиеся из другой из раздвоившихся структур, и с вероятностью 0.125  четыре структуры.

Энтропия будущего  растет огромными темпами. Ее правда можно искусственно уменьшить . если рассматривать второй и третий результаты событий   как одинаковые ( то же – для четвертого и пятого). И это тоже очень существенно. Итак, в нашем случае энтропия будущего растет очень быстро .

Во втором случае рассмотрения мы имеем следующее распределение вероятности после второго события.

1структура –0.25

2- структруры-0.375

3- структуры – 0.25

4- структуры – 0.125

 Отсюда мжно подсчитать энтропию будущего во втором варианте.

Теперь можно подсчитать энтропию настоящего

Перед первым событием энтропия настоящего равна ln2

В момент после произошедшего события энтропия настоящего раовна нулю.

Затем происходит расщепление.

1.Если структура осталась бех изменения . то перед вторым событием энтропия настоящего вновь оказывается равной ln 2.

2 Если структура расщепилась, то для каждой из появившихся структур появилась вероятность расщепиться с вероятностью 0.5 Таким образом, с вероятностью 0.25 не расщепится ни одна структура, с той же вероятностью расщепится первая из образовавшихся структур, с той же вторая, и с той же третья.

Энтропия настоящего вырастет в 2 раза.  И так далее.

Что мы видим из этого примера. Энтропия будущего – вещь относительно произвольная – зависящая от наших знаний. Энтропия настоящего зависит , на удивление, от числа сформировавшихсы структур ( если каждая из них является вероятностной (логической ) системой. И в нашем случае энтропия настоящего зависит не только от числа структур, но и от того, что произошло на предыдущем этапе, куда мы вышли в результате последующих действий. Энтропия настоящего может расти, оставаться постоянной и уменьшаться до нуля в зависимости от исходов предыдущих событий. В общем здесь все не так просто. Неопределенность – определенность- вновь неопределенность . Детерминизм- хаос – детерминизм.

   

Теорема о расщеплении волнового  вектора-матрицы на вероятностную и детерминированную части.

10

Вернемся к полученному нами вектору матрице и попробуем записать ее в несколько ином, более компактном виде.

Вектор – матрица, если взглянуть на него со стороны, представляет собой некую матрёшку из вложенных друг в друга вероятностных векторов и матриц действия. Эта матрешка в первом приближении может быть записана в виде


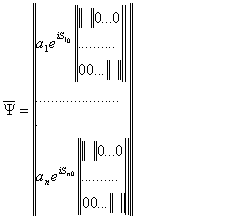
В выписанной структуре внутри между двойными вертикальными чертами вновь стоят вектор - матрицы с аналогичной структурой. Попытаемся записать полученное соотношение в символьном виде.

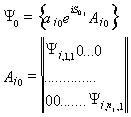
Здесь каждая вложенная  вектор- матрица, которая  может быть нами обозначена через  вновь имеет вид

 

Этот процесс может быть продолжен неограниченно до тех пор, пока в системе можно будет различать подсистемы все более низкого уровня иерархии.

Этот же процесс можно начать и продолжать и вверх, рассматривая более высокие ступени иерархии, в которые входит анализируемая нами система, состоящая из взаимодействующих структур. Этот процесс расширения может быть осуществлен следующим образом. Предположим, что наш вектор  включается в качестве, например, первого элемента в некоторую матрицу

 

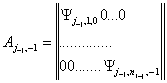
где сама матрица является элементом нового вектора

Этот процесс также может быть продолжен неограниченно вверх по уровням иерархии.

Тем самым, мы обнаружили еще одно очень интересное свойство нашего вектора - матрицы – возможность практически неограниченного расширения ее как вглубь – до самых мелких подструктур, так и наружу, путем включения в нее все более высоких уровней иерархии.

При этом, как было показано выше, остановка может быть сделана на любом уровне движения вглубь. Необходимо только свернуть по вышеуказанным правилам все остальные, не рассматриваемые нами глубинные уровни иерархии и заменить их соответствующими значениями действия и энтропии. В принципе, по-видимому, возможно нечто аналогичное выдумать и для внешних уровней иерархии, но это требует больших усилий.

 

 

Попытаемся  выполнить некоторые тождественные преобразования нашего вектора- матрицы, целью которых будет расщепление его на вероятностную и структурную части.


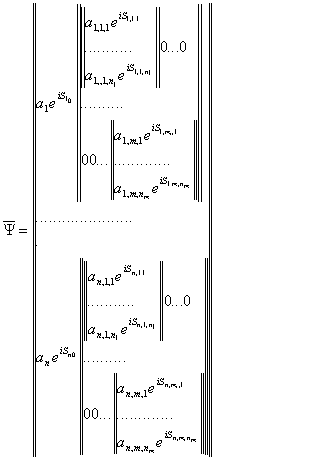
Может быть выполнено тождественное преобразование, которое приведет вектор-матрицу к виду:


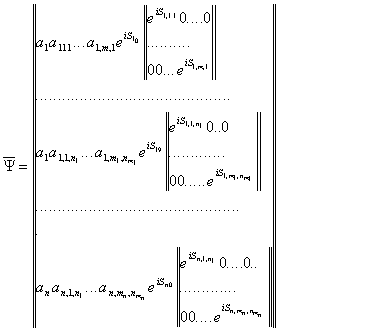
Тем самым мы путем тождественного преобразования привели вектор матрицу к новой форме, существенно отличающейся от первой. Эта форма представляет собой вероятностный вектор единичной длины , экспоненциальная часть каждой компоненты которого представляет собой комплексные матрицы с единичным модулем. Тем самым нам удалось отделить в рамках вектор -матрицы вероятностную и структурную части друг от друга. Вектор- матрица вновь стал «чистым» Можно показать, что энтропия –информация- действие полученного вектора- матрицы равна энтропии- информации- действию первоначального вектора-матрицы, что еще раз подтверждает корректность наших преобразований. Мы выполнили преобразование разделения только на одном этаже вектора-матрицы. По аналогичному сценарию такие преобразования могут быть выполнены для всей иерархической лестницы, на каждом ее этаже.

Тем самым доказана фундаментальная теорема .

Каждый иерархический  вектор- матрица всегда может быть представлен в такой расщепленной форме, которая позволяет разделить действительную вероятностную часть, представляющую собой действительный вектор с модулем , равным единице, по которой однозначно можно определить энтропию-информацию системы в данный момент времени, и комплексную детерминированную структурную часть, свою для каждой компоненты вероятностного вектора.

Подобное расщепление обосновывает принципиальную возможность на первом этапе исследования раздельно изучать вероятностную и структурную части мирового графа с возможностью затем их объединения в рамках единой вектор-матрицы и более компактного представления в иерархическом виде.

На наш взгляд выведенная теорема может стать основным ключом к математическому изучению графа взаимодействия.

Если действительная – вероятностная часть вектор-матрицы после преобразований , проведенных по всем уровням иерархии, сохраняет свою структуру и свойства, определяемые действительностью коэффициентов вектора вероятности и равенством его модуля единице (не здесь ли сидит причина того, что вероятностная энтропия-информация может быть описана единым последовательным алгоритмом?, однако и здесь первичная запись вектора-матрицы  позволяет вернуться к оператору энтропии-информации - действия и его иерархическому рассмотрению), структурная часть вектора- матрицы сохраняет свою иерархическую структуру и к ней  можно применять идеи эргодической теории- теории множеств с мерой., а также топологической и метрической теории динамических систем.

Итак, немного побывав в вероятностном мире, вернемся вновь к миру детерминированному, вооруженные доказанной нами теоремой о возможности расщепления детерминированного и вероятностного миров.

Однако, прежде чем это делать, сделаем некоторое интересное замечание, которое может оказаться нам в будущем очень полезным.

Благодаря выполненному нами расщеплению , можно утверждать следующее. В каждый момент времени будущего, прошлого, настоящего , в зависимости от условий рассмотрения ( и , возможно, масштаба времени)существует та или иная структурная матрица описывающая систему взаимодействующих структур. При этом с изменением времени происходит ( или должен произойти , если мы предсказываем будущее), переход из одной формы – матрицы структур в другую. Однако этот переход может происходить неоднозначно, с различными вероятностями казалось бы одно и то же состояние может переходить в разные состояния. Здесь можно (и нужно ) построить теорию многозначных отображений. То есть  одна точка отображается с различными вероятностями в разные точки. Построение такого типа многозначных функций возможно и мы уже начали его строить - очень интересно). Однако математики любят строить новое на уже построенном старом фундаменте. И здесь интересно вспомнить уже существующую теорию многозначных функций комплексного переменного. Она имеет два варианта . Один (не очень красивый) просто многозначные отображения с произвольным выбором одной из ветвей и другой – очень красивый – метод многолистных склеенных Римановых комплексных плоскостей. Кажущаяся в одной плоскости комплексная точка  z в этом новом рассмотрении оказывается проекцией бесконечного числа экземпляров «различных» точек , лежащих на различных листах риманова пространства. Тем самым одно пространство представляется нами в виде склеенных между собой почти идентичных пространств. Внутри  этой склейки точка может (в ином времени и в ином пространстве) принимать любое из бесчисленного множества значений, попадая на любой Риманов лист. Внешний наблюдатель никогда не знает , на каком листе она находится в момент совершения события (отображения), следовательно, он не знает однозначно, каков будет результат события. Тем самым мы предполагаем существование внутри структуры внутренней закрытой для внешнего мира возможности точки мгновенно перескакивать с одного риманова листа на другой, тем самым меняя исход события.

Эта идея может быть положена в качестве основной при создании математической модели вероятностных процессов, имеющих несколько  возможных исходов. Вместо одного множества, соответствующего данной структуре могут быть рассмотрены конечное или счетное число склеенных множеств, внутри которых точка может по  определённому закону  блуждать с очень большой скоростью (почти мгновенно) можно мыслить  себе вообще не одну точку , а их конгломерат, связанных между собой точек.

Внутри структуры как бы возникает внутренняя управляющая структура, с очень высокой скоростью функционирования, которая может в информационном плане очень интенсивно развиваться, базируясь на поступающей извне информации. Эта система имеет свою виртуальную структуру и свое виртуальное время, и может быть названа виртуальной информационной управляющей системой.

Ее механизм также может быть описан многозначными комплексными функциями. Но самое главное, такой подход дает возможность , добавив еще одно время, описать вероятностные процессы в терминах детерминированных, что упростит построение теории.        

 ]

 

 

                                                       .                                  

Этюд32

Целостный компьютер. Путь в Synergonet.

 

11 февраля 2011.

              

    Окружающая нас действительность представляет собой причудливое сочетание порядка и хаоса, детерминизма и неопределённости, закономерности и случайности. Стремление к познанию природы заставляет нас обращать внимание то на одну, то на другую сторону происходящих в ней процессов. Открытие Ньютоном основных законов классической механики, казалось бы, привело Человека к мнению, что Вселенной управляют законы, использование которых позволяет, в принципе, зная настоящее её состояние, однозначно определить как прошлое, так и будущее. Этот вывод, однако, во многом противоречил принципу свободы воли каждого отдельного человека, отрицая способность человека управлять своим будущим. Это принципиальное противоречие, не разрешённое полностью и в настоящее время, являлось и является до сих пор главным стимулом научных исследований. Попытки его разрешения уже привели и приведут в будущем к блестящим открытиям. Открытие законов Ньютона позволило описать основные закономерности движения природных объектов в виде решения дифференциальных уравнений, которое при заданных начальных условиях является однозначным. Это позволяет, в принципе, в рамках такого подхода как предсказывать будущее, так и угадывать прошлое. Философия, основанная на таком детерминистском подходе, объясняла «кажущуюся» неопределённость будущего неточностью наших знаний о настоящем. Казалось, что, чем более точно определить начальные данные в уравнениях Ньютона, тем точнее удастся предсказывать будущее. Эти надежды должны были реализоваться с появлением мощных компьютеров. Ведь программа компьютера представляет собой математическую модель детерминированной дискретной динамической системы, в частности, ею может быть реализована дискретная математическая модификация уравнений Ньютона. Алгоритм классической компьютерной программы устроен таким образом, что при введении одних и тех же начальных данных результаты расчётов должны оказаться идентичными. В этом смысле компьютерные расчёты являются столь же детерминированными, как и уравнения Ньютона. Тем самым, существовала надежда, что с возрастанием мощности компьютера удастся разрешить все научные проблемы. Однако, одновременно с развитием компьютерной техники росло понимание того, что здесь всё не так просто. Всё больше внимания учёные стали уделять исследованию неустойчивых динамических систем. Оказалось, что в таких системах любые сколь угодно малые отклонения в начальных данных приводят к конечным, а иногда стремящимся к бесконечности расхождениям в параметрах системы через конечный промежуток времени. Стало ясно, что ни один компьютер, сколь бы мощным он ни был, не может, в принципе, обеспечить однозначность даже в решении задач классической механики, которая являлась лишь первым приближением к более общим недетерминистическим законам квантового мира. Одновременно интенсивно развивалась качественная теория дифференциальных уравнений. Введение понятия фазового пространства позволяло построить общую картину траекторий динамической системы. Были обнаружены зоны, притягивающие к себе траектории, – аттракторы различных типов, - и зоны, выталкивающие из себя фазовые траектории - репеллеры. Кроме того, были найдены седловые зоны, которые первоначально притягивали, а затем выталкивали из себя фазовые траектории. При этом траектория, вышедшая из одной седловой зоны могла попасть в несколько альтернативных седловых зон или аттракторов. Глобальное качественное исследование динамических систем показало, что существуют такие зоны фазового пространства, где детерминизм уступает место неопределённости. И даже в рамках классической  механики обеспечить полный детерминизм оказалось невозможным. Простейшим случаем такого поведения является бифуркационное поведение динамической системы, когда с изменением одной из переменных в зависимости от времени аттрактор системы превращается в репеллер, а невдалеке от него формируются два новых аттрактора, При этом невозможно заранее предсказать, в каком из них окажется траектория системы. В этом случае можно ввести понятие вероятности того, к какому из новых аттракторов будет притягиваться траектория системы. У систем, близких к классическим Ньютоновым системам, таких зон нет или их количество невелико, и поэтому для их описания обычно бывает достаточно детерминированного подхода, с введением понятий вероятности лишь в отдельных бифуркационных точках фазового пространства, или проведения серии идентичных расчётов на классическом компьютере с очень слабо отличающимися исходными данными. Исключением являются странные аттракторы, демонстрирующие при детерминированном алгоритме поведение фазовой траектории, подчиняющееся вероятностным законам.

    По-другому ведут себя системы, описываемые большим числом независимых переменных. В этом случае число аттракторов, репеллеров и седловых зон становится настолько большим, что даже кажущаяся нам детерминированной система, например, система твёрдых тел, может обладать траекториями, имеющими случайный характер. К описанию динамики таких систем, даже если они, в принципе, описываются детерминистическими дифференциальными уравнениями, рационально применять статистические методы. 

    Однако в природе существуют самоорганизующиеся системы. Сюда относятся все живые системы, которые могут существовать только в определённых зонах фазового пространства, а вне этих зон они разрушаются. Для обеспечения устойчивости такой системы внутри неё выделяется подсистема, названная нами контроллером, способная таким образом изменять своё фазовое пространство, чтобы максимально увеличить вероятность того, чтобы основная часть системы оставалась в благоприятной для неё зоне фазового пространства. Обычно такие системы являются открытыми, то есть их существование сопряжено с взаимодействием с другими системами, входящими в поле данной системы, то есть находящимися вне неё. Принцип действия таких систем может быть описан следующей целостной триадой Р. Г. Баранцева [1, 2]:

 

 

Поле

/             \

Основная структура-----Контроллер

 

Фазовое пространство основной структуры определяет границы существования системы. Чем дальше состояние основной структуры от границы, тем устойчивее система к неблагоприятным внешним воздействиям со стороны других систем, входящих в её поле. Контроллер играет в такой самоорганизующейся системе роль информационной и управляющей подсистемы, опережающей неблагоприятное воздействие поля и таким образом меняющей фазовое состояние основной структуры, чтобы точка её фазового пространства находилась как можно дальше от границы устойчивости.  «Цель» контроллера - сохранение стабильности основной структуры и продление срока существования системы в целом. В реальных самоорганизующихся системах полное отделение основной структуры от контроллера и поля невозможно. Здесь действует принцип дополнительности, обобщающий аналогичный принцип неопределённости квантовой механики. Однако, в первом приближении можно выделить фазовые пространства, описывающие отдельно основную структуру, контроллер и поле. Общее фазовое пространство большой системы может быть приближённо описано как произведение соответствующих фазовых пространств. Если спроектировать это пространство на фазовое пространство основной структуры, то можно установить корреляцию между вероятностью нахождения основной структуры в той или иной точке своего фазового пространства и состояниями поля и контроллера. При таком подходе поле является внешней подсистемой, которая, взаимодействуя с самоорганизующейся системой, может вывести её за границы устойчивости и тем самым разрушить её.

     Контроллер осуществляет мониторинг фазового пространства поля и основной структуры, выявляет наиболее опасные для самоорганизующейся системы тенденции в изменении фазового пространства поля и основной структуры. Он изменяет своё состояние таким образом, чтобы состояние основной структуры находилось на максимально возможном в данных условиях расстоянии от границы устойчивости системы.

    Рассмотрим, как может выглядеть в общем виде математическая модель такой целостной самоорганизующейся системы. Пусть в начальный момент времени основная структура находится в некотором начальном состоянии. В следующий момент времени она переходит в новое состояние. Каково будет это новое состояние, зависит не только от предыдущих состояний основной структуры, но также от состояний поля и контроллера.        Это условие может быть представлено в вероятностной форме. Переход из начального состояния в любое другое состояние основной структуры определяется некоторым числом, большим или равным нулю и меньшим или равным единице, которое называется вероятностью перехода. Сумма таких чисел, взятых по всему фазовому пространству основной структуры, равна единице. Изменение состояния поля и изменение состояния контроллера приводят к изменению распределения вероятностей перехода от одного состояния основной структуры к другому. Взаимодействие целостной системы с полем, состояние которого не может быть полностью контролируемо системой, может приводить как благоприятным, так и неблагоприятным последствиям, к благоприятному или неблагоприятному изменению распределения вероятностей перехода в фазовом пространстве основной структуры. При наличии контроллера целостная система имеет возможность управлять состояниями его фазового пространства таким образом, чтобы повысить устойчивость основной структуры.

    Изложенные выше принципы могут лечь в основу идеи целостного компьютера [2, 3]. По аналогии с классическим и квантовым компьютером [6] основным элементом такого компьютера может стать целостный элемент с двумя возможными состояниями, каждое из которых может реализоваться с определённой вероятностью. Такой элемент  назван нами C - битом. Этот элемент имеет двойственную природу. Даже в случае, когда вероятность реализации того или иного состояния постоянна во времени, каждая новая реализация может отличаться от предыдущей. Целостный компьютер должен иметь квазифрактальную структуру: целостный характер должен иметь каждый уровень иерархии его подсистем. Из совокупности элементарных С-битов могут быть построены целостные слова, целостные предложения и т. д., имитирующие системы различных масштабных уровней , участвующих в событиях с конечным числом возможных исходов.

    Полем для такого компьютера могут служить внешние устройства, позволяющие в любой момент принудительным образом менять как текущее состояние основной структуры компьютера, так и вероятности перехода из одного состояния в другое, или выполняющая ту же функцию внешняя часть целостного компьютера.

    Контроллером такого компьютера должна быть та его часть, изменение состояния которой является, в основном, функцией от внешних воздействий. Это изменение производится таким образом, чтобы достигнуть такого распределения вероятностей реализации состояний основной структуры, при которых более вероятными стали наиболее жизнеспособные состояния, то есть состояния, находящиеся на максимально возможном удалении от границ области их существования.

    В отличие от моделируемой самоорганизующейся системы, которая может иметь бесконечное число состояний, целостный компьютер в классическом варианте исполнения (не исключён вариант исполнения в виде квантового компьютера [6]) будет иметь, хотя и очень большое, но конечное число возможных состояний. В этом смысле, так же как и в случае классического компьютера, для него возникает принципиальная проблема соответствия математической модели реальной целостной динамической системе. Однако, опыт использования классических компьютеров показывает, что аппроксимация конечным числом элементов кажущихся нам непрерывными процессов и систем даёт в большинстве случаев блестящие результаты. Поэтому проблему соотношения бесконечного и очень большого, но конечного числа элементов вынесем за рамки нашего рассмотрения.

    Предположим, что общий массив состояний целостной системы и окружающего её поля может быть при моделировании с помощью целостного компьютера представлен в виде произведения массивов состояний основной системы, контроллера и поля. В каждый момент времени компьютерная модель системы и поля находится в одном из возможных состояний. Как и любая динамическая система, компьютерная модель в виде целостного компьютера, на следующем шаге рассмотрения изменяет своё состояние на другое, включённое в массив возможных состояний. В целостном компьютере, в отличие от классического должно существовать принципиальное отличие прошлого от будущего. Прошлое принципиально определено, детерминировано, и информация обо всех прошлых состояниях системы должна храниться в памяти компьютера. В этом случае нет никакого отличия от классического компьютера. Будущее же, в принципе, не определено и знание о будущем может быть получено с определенной степенью вероятности. Поэтому в целостном компьютере должны присутствовать массивы вероятности перехода из одного состояния модели в другое. Наряду с этим должен быть предусмотрен вычислительный механизм, позволяющий для каждого конкретного расчёта на каждом шаге по времени осуществлять выбор нового состояния.

    Разбиение общего массива состояний на три части позволяет в самом общем виде определить особенности действия целостного компьютера и моделируемой им целостной системы, наблюдая, насколько это возможно, отдельно за динамикой основной структуры, контроллера и поля.

    Пусть в некоторый момент времени в памяти целостного компьютера зафиксированы состояния основной структуры, контроллера и поля. Требуется определить, каковы будут эти состояния на следующем шаге по времени. Разобьём этот шаг на две части: основной и упреждающий. В упреждающий момент времени определим распределение вероятности перехода контроллера в новое состояние, зависящее в соответствии с заданным алгоритмом от состояния системы и поля в данный момент и все предшествующие моменты существования моделируемой системы и поля. Затем воспользуемся существующим в памяти целостного компьютера механизмом реализации случайного события, позволяющего спроектировать многомерный вектор распределения вероятности на одно  из возможных состояний контроллера, то есть сделать неопределённое будущее состояние контроллера настоящим. В результате получим новое состояние контроллера в упреждающий момент времени. Далее, в основном шаге по времени, вычислим по заданному алгоритму векторы распределения вероятности достижения определённых состояний основной структуры и поля в функции от состояний системы и поля во все предшествующие моменты времени, в том числе для контроллера на упреждающем шаге. Затем вновь воспользуемся механизмом реализации случайного события и определим новое состояние основной структуры и поля. Этот алгоритм, в основном, повторяется на следующем шаге по времени.  Единичный расчёт на целостном компьютере даёт один из возможных вариантов динамики самоорганизующейся системы и её поля. Повторяющиеся расчёты дают возможность получить статистические данные о поведении популяции целостных систем данного класса, формирующих обобщённую волну [3, 9]. Изменяя алгоритмы вычисления векторов распределения вероятности, можно обеспечить максимальную выживаемость модели, а, следовательно, и самой самоорганизующейся системы.

    Возникает вопрос, как целостный компьютер связан с классическим, и можно ли, находясь в рамках парадигмы классического компьютера, построить целостный. На наш взгляд, такая возможность не только существует, но стихийным образом всё в большей степени реализуется с развитием компьютерной техники. Если первые компьютеры  с детерминированными программами были в максимальной степени классическими, то с развитием компьютерной техники, переходом к персональным компьютерам, а затем к сетям, случайные элементы всё в большей степени вводились в динамику компьютера. Роль поля и контроллера во всё большей степени стал играть человек, способный произвольно включать в работу различные алгоритмы, вводить в компьютер в процессе работы различные исходные данные, анализировать результаты, изменять алгоритмы программ.  Особенно ярко эти новые свойства проявились при возникновении и развитии Internet, которую по праву можно считать одной из самых сложных из известных нам самоорганизующихся систем.

    Контроллером и частично полем Internet является Человечество, которое в свою очередь представляет собой целостную самоорганизующуюся систему. Поэтому совокупность Человечество- Internet можно считать гигантским целостным суперкомпьютером, который нами и И. И. Шиловичем был назван Synergonet [4, 5]. Однако, Synergonet пока развивается по законам, определяемым его контроллером – Человечеством, хотя её обратное воздействие на эти законы уже становится очевидным. Если каждый персональный компьютер станет целостным и его контроллер будет действовать независимо от человека, то Synergonet начнёт развиваться по своим законам, которые могут прийти в противоречие с интересами  Человечества. Человек в этом случае может стать ненужным придатком сформировавшейся новой целостной системы. Этот процесс уже происходит на наших глазах. Его обнаружение и мониторинг должны стать одним из важнейших элементов обеспечения безопасности Человеческой популяции [7, 8, 9].

 И это поняли руководители Восьмёрки, включившие проблему будущего Internet (Мы бы добавили сюда Synergonet) в программу своей встречи 26 мая 2011 года.

 

Литература.

 

1.Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

2. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168 с.

3.Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. СПб.: Норма. 2002. 144 с.

4. Басин М. А., Шилович И. И. Синергетика и Internet. (Путь к Synergonet). СПб.: Наука. 1999. 71 с.

5. Басин М. А., Шилович И. И. Путь в Synergonet. СПб.: Норма. 2004. 128 с.

6. Стин Э.Квантовые вычисления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика». 2000. 112 с.

7. Басина Г. И., Басин М. А. СПб.: Синергетика. Эволюция и ритмы Человечества. Норма. 2003. 260 с.

8. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.

9. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

Этюд 33

 

Структура . Поле.Контроллер

 

 

21 марта 2011.

 

Всякая самоорганизующаяся система обменивается с окружающей средой (полем) материей, энергией и информацией. Введение при анализе системы и поля времени в качестве основного параметра, определяющего динамику системы, наряду с непрерывным фазовым пространством, позволяет обратить внимание на одну очень важную особенность взаимодействия системы и её поля – на волновой характер выделяемых нами из окружающей природы структур [2].

Детальное качественное и количественное исследование взаимодействия полей и структур должно проводиться в рамках континуальных моделей, то есть для его математического описания должен использоваться аппарат линейных и нелинейных дифференциальных уравнений в частных производных и связанных с ними бесконечномерных математических групп преобразований. Однако, получение и анализ решений этих уравнений на первых этапах исследований часто оказывается нецелесообразным, а иногда, и невозможным. Более адекватным в этом случае является использование качественных методов, которые, в частности, включают классификацию волновых структур, порождаемых континуальными полями.

Нами предложена классификация волновых движений, структур и систем, опирающаяся на их общие волновые свойства, в рамках которой удалось проследить за характером влияния нелинейности на переход от классических линейных волновых движений к динамическим структурам и сложным самоорганизующимся транспортно-информационным системам.

Классификация проводится по трём параметрам:

- по типу;

- по характеру взаимодействия с другими системами;

- по степени нелинейности.

 

I. Классификация по типу:

1. Обобщённые волны, представляющие собой классы идентичных или почти идентичных объектов (квантов).

2. Вероятностные волны, характеризующие изменение плотности вероятности (или эквивалентной ей волновой функции) отыскания системы или структуры в одном из возможных для неё состояний из континуума допустимых состояний системы.

3. Классические волны в сплошной среде, характеризующие изменение во времени и пространстве плотности какого-либо параметра или связанной между собой системы параметров сплошной среды.

 

II. Классификация по характеру взаимодействия с другими системами, аналогичная классификации конечномерных динамических систем:

 

1. Свободные (собственные) волны.

2. Вынужденные волны.

3. Автоволны.

 

 

II.  Классификация по степени нелинейности.

 

1. В качестве первого класса рассматриваются все волны относительно малой амплитуды, математическое описание которых может быть дано в виде совокупности решений линейных волновых уравнений в частных производных.

2. Ко второму классу, названному нами умеренно - нелинейными волнами, отнесены различные формы ударных волн в сплошных средах, солитоны, а также скачки тех или иных параметров в однородной среде и границы раздела сред. В качестве подкласса сюда могут быть отнесены диссипативные континуальные структуры и структуры, формируемые в результате возникновения режимов с обострением [3]. Предельным случаем такого типа волн является гипотетическая суперударная комплексная волна, описанная в Этюде .

3. К третьему классу, названному нами вихревыми ударными волнами (вихревыми структурами), отнесены вихревые (спиновые) структуры и структуры с угловыми точками, формируемые вследствие пространственной потери устойчивости и гладкой формы умеренно - нелинейных волн.

4. К четвёртому классу, названному нами грибовидными структурами, отнесены структуры мультипольной природы, формируемые из совокупности вихревых структур и умеренно нелинейных волн. Различные модификации и комбинации структур такого типа составляют основу практически всех объектов живой и неживой природы.

5. К пятому классу отнесены структуры, названные нами древовидными (или сетевыми), бифуркационная динамика которых может быть описана методами математической теории сетей и графов, в частности при помощи теории математических деревьев [8].

6. К шестому классу мы отнесли сложные самоорганизующиеся системы, названные нами транспортно - информационными, являющиеся результатом трансформации и взаимодействия вихревых, грибовидных и древовидных структур и волн более низких классов.

Несмотря на то, что четвёртый, пятый и шестой классы структур и систем встречаются и в неживой природе, наиболее широко они распространены в биологических и социальных системах. Поэтому общие закономерности их динамики оказываются важными не только для физических и химических исследований, но, главным образом, для наук о Земле, биологии и наук о человеке и обществе.

Описанная  классификация нелинейных волн, структур и систем включает в себя в качестве шестого класса транспортно-информационные системы. К этому классу относятся реки и моря, атмосфера, гидросфера, живые организмы (в том числе и человек), биоценозы, а также производственно-транспортные системы социума, экономика, язык, культура, Internet, Synergonet (смотри этюд 32), планеты, звёзды, галактики, Вселенная.

    При этом включение транспортно-информационных систем в общую классификацию волновых движений позволяет рассматривать их свойства и динамику их развития с единых позиций, применимых к любым структурам, обладающим волновыми свойствами. Они являются одной из наиболее характерных, а, возможно, единственной формой самоорганизующихся систем, обеспечивающей существование грибовидных структур. Последние, в частности, представляют собой совокупность вихревого тора (диполя) и «ножки», связывающей эту структуру либо с материнской границей, либо с другими грибовидными структурами. Совокупность связанных между собой грибовидных структур обычно образует многополюсную транспортно-информационную систему, представляющую собой ряд дипольных центров (шляпок грибовидных структур) и связывающие их транспортные артерии – ножки грибовидных структур.

В качестве примера приведём данное М. А. Басиным и И.И. Шиловичем [5, 6] определение Internet:

«Это большая сложная транспортно-информационная система из грибовидных (дипольных) структур, шляпка каждой из которых (собственно диполи) представляет собой мозг человека, сидящего за компьютером (или мобильным телефоном), в совокупности с самим компьютером (или мобильным телефоном), который как бы является искусственным продолжением мозга, а ножки, например, телефонная сеть, соединяющая компьютеры, или эфир, через который передаются радиоволны (от сотового телефона)» .

Разветвлённая транспортно-информационная система, во- первых, покрывает достаточно густой сетью ту часть поверхности или пространства, в которых она расположена, а во-вторых обеспечивает управляемый транспорт материи, энергии и информации к любым элементам системы. На наш взгляд, именно развитие транспортно-информационных систем и является единственным способом, который придумала природа, а за ней и человек, для преодоления всеобщего роста энтропии, а также выработки и быстрой передачи не только материи и энергии, но и информации.

Каковы же с этих позиций основные свойства транспортно-информационных систем?

А) Открытость системы. Система обычно устроена таким образом, что в узлах системы (полюсных шляпках грибов) происходит обмен материи, энергии и информации, поступающей извне и (или) вырабатываемой внутри системы.

Б) Существуют собственные транспортные элементы системы - ножки грибов, покрывающие тонкой сетью или несколькими слоями всю площадь или объём, занимаемый транспортной системой, которые осуществляют функцию доведения материи, энергии и информации до каждого элемента транспортной системы.

В) Возможно разделение функций выработки, приёма, переработки и передачи материи, энергии и информации между отдельными элементами системы, резервирование функций.

Г) Транспортные системы по мере усложнения формируют иерархическую структуру – как сама транспортная система, так и её элементы и подсистемы представляют собой грибовидные и древовидные (сетевые) структуры различных масштабов.

Д) Иерархичность транспортно-информационных систем определяет квазифрактальность их геометрии, то есть полное или частичное подобие структур в разных масштабах.

Создаваемые человеком транспортные системы, в том числе и экономика, должны строиться таким образом, чтобы учитывать указанные выше свойства естественных систем.

Необходимость выживания в условиях изменения внешней среды заставляет транспортные системы вырабатывать внутренние информационные управляющие механизмы - контроллеры. Всякой самоорганизующейся транспортно-информационной системе можно сопоставить целостную триаду [1]:

 

 

Поле

(Ближнее и Дальнее)

/                     \

Структура-------------Контроллер

(Основная часть системы)-----------(Управляющая подсистема).

 

Структура (основная материальная часть системы) - часть системы, которая взаимодействует с полем, в основном, на материальном и энергетическом уровне.

Поле (ближнее и дальнее) – это внешняя по отношению к системе совокупность объектов, интенсивно взаимодействующих с системой. Поле может быть условно разделено на ближнее и дальнее. Для исследования взаимодействия дальнего поля с системой могут быть использованы асимптотические методы.

Контроллер (управляющий механизм) – внутренний механизм системы, обеспечивающий выбор из числа возможных исходов бифуркационного события или процесса того, который приведёт к наиболее устойчивому состоянию системы.

Появление контроллера включает в действие механизм эволюции. Развиваются в непосредственной связи между собой все три элемента триады. Возникает тройное резонансное взаимодействие (по-видимому, здесь действует механизм структурно-волнового резонанса), приводящее к увеличению сложности и динамической устойчивости (увеличению числа возможных исходов бифуркационных событий  и увеличению количества информации, хранимой и перерабатываемой контроллером) [8,9].

Транспортно-информационные системы, в свою очередь, могут быть классифицированы по степени нелинейности (сложности).

1. Системы квази - детерминированного типа, бифуркационные процессы внутри которых оказывают лишь интегральное влияние на их макропараметры. Основным свойством таких систем является значительная разница между масштабами самой системы как обобщённой волны и отдельными элементами (квантами), её формирующими, а также близость параметров квантов. Границы таких систем, являющиеся обычно волновыми структурами, относящимися ко второму и третьему классу предложенной нами классификации, во многом определяют их динамические свойства. Для изучения систем квазидетерминированного типа существуют глубоко разработанные методы равновесной и неравновесной статистической физики и механики сплошных сред. Большинство макроскопических объектов неживой природы относится к этому подклассу.

2. Транспортно - информационные системы, у которых реализуется иерархическая материальная и информационная связь между уровнем системы-волны и элемента-кванта. В таких системах обычно выстраивается масштабная иерархия подсистем, каждая из которых может обладать волновыми свойствами структур классов более низкой степени нелинейности. Эта масштабная иерархия имеет квазифрактальный характер, то есть на разных уровнях иерархии существует частичное подибие подсистем. Кванты в таких системах более сложны и разнообразны, чем в системах первого подкласса.

3.Транспортно-информационные системы, способные к размножению, то есть к формированию себе подобных систем. Способность к размножению не является прерогативой только транспортно-информационных систем. Практически это свойство в той или иной степени характерно для любых колебательных и волновых систем, начиная с линейных колебаний и волн. Однако, когда мы переходим к рассмотрению транспортно-информационных систем третьего подкласса, то их размножение может иметь специфический характер, проявляя, особенно у живых систем, такую сложность, которую невозможно даже помыслить у волн и структур более примитивных классов.

4.Транспортно-информационные системы, способные моделировать свою динамику и динамику окружающей среды - поля и выбирать близкие к оптимальным  модели бифуркационного поведения. Именно у таких систем интенсивно развивается, определяя их эволюцию, внутренний контроллер.

5. Транспортно-информационные системы, обладающие сознанием и творческими способностями.

Так как возникновение и эволюция контроллера является принципиально важным фактором, отличающим сложные транспортно-информационные системы, то причины его появления и механизм действия требуют специального рассмотрения. Если бы все события  в природе были детерминированы, а процессы, происходящие со всеми структурами, были заранее предопределены, то никакой потребности в контроллере бы не возникло. Информация и представление о ней возникают только как следствие существования неопределённости при совершении бифуркационных событий.

Однако это только одна сторона информационного процесса. Возможность существования в природе бифуркационных событий и процессов порождает принципиальную неполную предсказуемость будущего, а следовательно, возможность управления будущим путём выбора одного из возможных исходов. Возникает  необходимость вероятностного предсказания будущего – знания о будущем. Переход от информации о прошлом к информации о будущем, знанию, - это творческий процесс. Резкий скачок информации о будущем может произойти без дополнительного получения информации о прошлом и наоборот, можно получать бесконечное количество информации о прошлом, не извлекая из неё знания. (это может быть проиллюстрировано качественно на примере суперударной волны (этюд  )

При изучении системы, управляемой контроллером, необходимо не только анализировать динамику её основной материальной структуры и строить соответствующие математические модели, но также знать принципы действия контроллера и уметь моделировать процесс создания им моделей поведения. Здесь возникает новая триада

Исследователь

/                \

Структура--------------Контроллер

 

Вся окружающая нас действительность представляет собой синергетическое взаимодействие волн, структур и систем различной природы. В качестве примера могут быть рассмотрены последние катастрофические события. Взаимодействие небесных тел: Земли и Луны, наложившееся на внутренние процессы, происходящие в Земной коре, привели к землетрясению - возникновению разрывов в Земной коре – формированию вихревых ударных волн третьего класса. Воздействие этого процесса на поверхность океана породило мощную уединённую волну (солитон) - цунами. Резонансное воздействие этих волновых структур на побережье Японии привело к значительным разрушениям в транспортно-информационной системе, созданной японским этносом, одной из подсистем человеческого общества. Одновременно погибли тысячи людей, транспортно-информационных систем значительно меньших масштабов, но обладающих наивысшей из известных нам степенью нелинейности. Однако эти события имеют продолжение и оказывают своё влияние на всю биосферу Земли и всё человеческое общество. Частичное разрушение информационно-транспортной структуры Японских островов привело к возмущениям в экономике Японии и отразилось на котировках ценных бумаг на биржах всего мира. Частичное разрушение атомной электростанции в Японии привело к нарушению управления ядерной реакцией и опасности неуправляемых процессов ядерного взрыва – формирования грибовидных структур больших масштабов,- что, в свою очередь может привести к необратимым изменениям в биосфере и человеческом обществе. Если подобные волновые возмущения смогут быть погашены контроллером человечества, то все разрушения инфраструктуры будут нивелированы, если нет, то цепочка катастрофических событий, в которых возникают и взаимодействуют волны, структуры и системы различных классов, будет продолжена.

  

Литература.

 

1.Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

2.Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168 с.

3. Режимы с обострением. Эволюция идеи. Законы коэволюции сложных структур. М,: Наука.1999. 256 с.

4.Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144 с.

5. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71 с.

6. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.

7. Басина Г. И., Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с.

8. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.

9. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с

 

 

 

 

Этюд 34

 

Вихре-волновой и (или) структурный резонанс. Нана - технологии. Жизнь. Экономика.

 

5 апреля 2011.

 

При качественном анализе влияния нелинейности на динамику систем с континуальным множеством координат нами предложена новая классификация волн, структур и систем, опирающаяся на их общие волновые свойства, в рамках которой удалось проследить за характером влияния нелинейности на качественный переход классических линейных волновых движений в динамические структуры и сложные самоорганизующиеся транспортно- информационные системы. (Смотри Этюд №).

Предложенная классификация позволила объяснить ряд новых физических явлений, обнаруженных при исследовании взаимодействия сложных систем и их полей как резонансное вихре - волновое взаимодействие. Построена классификация резонансных явлений в динамических системах и волновых структурах, куда включён открытый нами новый широкий класс, названный вихре - волновым и (или) структурным резонансом. Исследованные теоретически и экспериментально примеры вихре - волнового резонанса при движении несимметричных тел в сплошной среде свидетельствуют о возможности существования вихре - волновых и (или) структурных резонансных явлений при взаимодействии произвольных близко расположенных структур, находящихся в некотором общем поле, через которые они могут воздействовать друг на друга.[1, 2]. При выполнении условий появления резонансов такого типа может происходить качественное изменение параметров взаимодействующих структур и систем, что может быть использовано при создании новых технологий в различных областях человеческой деятельности.

Необходимым условием структурного резонанса является равенство эквивалентных размеров (длин присоединённых волн) взаимодействующих структур. Для проверки возможности появления структурно-волнового резонанса достаточно знать основные параметры поля, в котором расположены взаимодействующие структуры, основное уравнение, описывающее динамику поля, и найти собственный спектр волн, характеризующих это поле. 

Воздействие структур на поле обычно описывается интегральными операторами, характеризующими изменение поля под действием движущихся и излучающих структур. При этом не все параметры структур, воздействующих на поле, должны быть закреплены. В этом случае обратное действие поля на структуру может резонансно резко изменять не закреплённые параметры структуры.

 Резонансное взаимодействие приводит к отбору и усилению параметров, соответствующих волновым частотам, длинам волн и размерам структур, которые являются близкими для резонансно взаимодействующих объектов. Отсюда справедливо не только утверждение о том, что вихре - волновой и (или) структурный резонанс может быть использован для обнаружения слабых неоднородностей в сплошных средах и полях различной природы, но также утверждение о том, что, если такой отбор и такое усиление в каких-либо явлениях наблюдается, то сам этот факт может служить сигналом, проявляющим вихре - волновой и (или) структурный резонанс.

Рассмотрим некоторые возможные сферы применения сделанного открытия.

 Одной из важнейших функций головного мозга является   распознавание в потоке поступающей информации образов реально существующих предметов. Механизм распознавания образов до настоящего времени полностью не раскрыт. Поэтому новые идеи, связанные с решением этой задачи, заслуживают пристального внимания. Предлагается в качестве одного из вариантов решения этой проблемы использовать одну из форм вихре - волнового и (или) структурного резонанса,  так называемый экранный эффект, то–есть значительное увеличение подъёмной силы крыла при приближении его к экрану. Как следует из теоретического рассмотрения соответствующей математической задачи и результатов экспериментальных исследований, влияние экрана на гидродинамические характеристики крыла эквивалентно влиянию отраженного от экрана крыла, обтекаемого под противоположным углом атаки [3]. Если расположить вблизи некоторой плоскости два крыла, то максимальное взаимодействие, приводящее к взаимному аномальному увеличению их несущей способности, будет наблюдаться именно в резонансном режиме, когда их размеры будут одинаковы и они будут симметричны относительно этой плоскости. Математическая модель обтекания системы крыльев в настоящее время хорошо разработана и может быть использована для создания принципиально нового метода распознавания образов. Сделанное предложение требует специальной проработки и дополнительной оценки его эффективности.

Транспортно-информационные системы представляют иерархию волновых процессов с различными частотами и структур с различными масштабами, взаимодействующих между собой. Это внутреннее взаимодействие также обычно осуществляется резонансным образом, за счёт связей соседних уровней иерархии и комбинационных резонансов, позволяющих перейти от заданных частот возмущения и масштабов (волновых чисел) к другим. В этом случае резонансное взаимодействие может привести к качественному изменению поведения как отдельных элементов или подсистем или поведения системы в целом.

 Вихре-волновой и (или) структурный резонанс может проявиться и иметь свои специфические формы при любых перемещениях произвольных структур в неоднородной сплошной среде, что даёт возможность применять основные теоретические положения, позволяющие изучать это нелинейное явление применительно к судостроению и авиации, техническим производствам, химии, биологии, нана-технологиям, физике и магнитной гидродинамике, океанологии и метеорологии, экономике и другим социальным процессам.

Предсказанное теоретически и обнаруженное экспериментально явление вихре-волнового и (или) структурного резонанса внесло коренные изменения в существующие представления о динамике движущихся объектов и неоднородной сплошной среды. Открытие этого явления стимулирует создание и развитие новых методов теоретических и экспериментальных исследований в различных областях науки и техники, созданию новых технологий и конструкций.

Концепция вихре-волнового и структурного резонанса, а также  классификация нелинейных волновых движений используются для объяснения  известных, но не изученных до конца нелинейных явлений, связанных с движением тел в жидкости: отрывное обтекание тел, возникновение и развитие циркуляционного течения около тела, возникновение и разрушение ударных волн на границе раздела сред, обтекание интерцепторов, гидроупругие колебания крыльев [2].

Значение полученных результатов состоит не только в обнаружении и изучении нового неизвестного ранее класса резонансных процессов и вихре-волновых структур, но также и в том, что разработанная классификация волновых движений и вихревых, грибовидных и древовидных структур позволяет предсказывать и обнаруживать неизвестные ранее формы вихре-волнового взаимодействия, создавать искусственно условия для возникновения этого типа резонансов применительно к практическим задачам, а также создавать новые способы,  разрабатывать новые конструкции, часть которых уже использована в судостроении.

 В последние годы учёные, проектировщики, бизнесмены и даже политики значительное внимание уделяют развитию нана -технологий. Одним из возможных путей развития нана-технологий является попытка перенесения технических достижений классической и ядерной науки и техники в переходный мир нана-структур. Однако наибольший эффект может быть достигнут, если обратить внимание на резонансные явления в этих промежуточных по пространственным масштабам процессах.

В частности, неограниченные практически полезные результаты может дать исследование в нана- масштабах условий возникновения и эффективного воздействия на нана-структуры вихре-волнового  и (или) структурного резонанса. Теоретические и экспериментальные исследования геометрических и частотных характеристик нана-структур позволят уже на первых этапах исследования предсказать условия появления вихре - волнового и (или) структурного резонанса и в первом приближении оценить возможные эффекты, связанные с его появлением.  Вихре - волновой и (или) структурный резонанс в нана - масштабах позволит локально концентрировать в заданном месте значительные запасы энергии, а также необходимые для тех или иных реакций вещества, молекулы и атомы.

   Резонансные процессы, являющиеся комбинациями масштабных, вихре-волновых и структурных резонансов, широко распространены в биологических и социальных системах.  Наиболее ярким примером применимости концепции вихре – волнового и (или) стрктурного резонанса может стать проблема возникновения живого. Изложим некоторые гипотезы.

Важную роль здесь играют резонансные нелинейные процессы формирования и деформации границ, приводящие к росту информации. Двумерные границы рассматриваются в нашей классификации как одна из форм умеренно нелинейных ударных волн. В формировании и динамике резонансных грибовидных структур границы несут главную информационную нагрузку, которая для живых организмов является основной и постоянно развивающейся. Еще большую информацию несёт линия, представляющая собой пересечение двух границ. Но максимальная информационная нагрузка возникает в точке или малой области, в которой пересекаются три границы.

    Существуют ли такие области в Природе? Да. Если мы рассмотрим четыре стихии Аристотеля: земля, вода, воздух и огонь,- то пересечение границ между ними должно привести к появлению малой особой области, в которой формируются структуры, элементы которой обладают максимальной неоднородностью. Побережье Мирового Океана и побережья локальных водных пространств могут рассматриваться как линии пересечения двух границ. Если в этой области локально добавить «огонь» в виде Солнечного света или вулканических извержений (проблема «чёрных курильщиков»), то реально создаются условия для возникновения и длительного существования разнообразных резонансных форм устойчивых в своей неустойчивости вихревых, грибовидных и древовидных структур, которые можно отождествить с одной из форм живых организмов.

   Эта гипотеза требует детальной проработки и может явиться основанием для формирования нового направления в изучении важнейшей научной проблемы возникновения жизни. Если она подтвердится, то подобный механизм может быть использован для создания принципиально новых нана – технологий, имеющих дело с объектами, лежащими на границе живого и неживого.

     Однако это не единственное направление подобных исследований. Анализ динамики популяции клеток и организмов в условиях ограниченного ресурса также позволяет обнаружить резонансный путь развития. Этот путь избрала природа при создании многоклеточных животных и растений. По этому же резонансному пути, возможно, пойдёт и человеческое общество, столкнувшись с экономическим кризисами, нехваткой материальных ресурсов и ограничениями численности популяции. Формирование мегаполисов, появление и интенсивное развитие Internet с возможным переходом в Synergonet, передача всё большего числа функций международным организациям – являются свидетельствами резонансной самоорганизации, а также интенсивного развития и качественной трансформации единого общего       для всего человечества контроллера. Об этом же говорит глобальность и синхронность проявлений структурного кризиса, с которым столкнулось человечество в настоящее время. Так, например, революции в  различных арабских странах произошли практически одновременно.

    Пусть пространство, в котором популяция клеток или организмов может использовать природные ресурсы, ограничено и отделено от другого аналогичного пространства значительной зоной, в которой получить ресурсы для существования невозможно. Характерным примером является слизневик Dictyostelium disclodeum, который может существовать как в форме отдельных клеток (нерезонансный режим), так и в форме единого организма (резонансный режим) [4]. В фазе роста, когда ресурса достаточно, каждая отдельная клетка слизневика существует как отдельная особь. Их распространение по поверхности осуществляется по закону движения свободной биологической волны: они размножаются по экспоненциальному закону, занимая всё большую площадь. Однако, когда ресурса начинает не хватать, система переходит в состояние резонансной самоорганизации. Одна из клеток становится пейсмекером [5] центром структурно - волнового резонанса. Испуская специфические вещества, она создаёт новое биологическое поле, резонансно притягивает к себе остальные клетки. Формируется многоклеточная грибовидная структура, клетки которой расположены впритык друг к другу, что позволяет им поддерживать обмен веществ при значительно меньших затратах энергии, чем при независимом существовании. Тем самым внешней средой для внутренних клеток становятся резонансно с ними взаимодействующие клетки, имеющие те же размеры и синхронизированный с ними темп обмена веществ. Резко уменьшается поверхность соприкосновения популяции с внешней средой. Каждую внутреннюю клетку кормят её соседи или  вновь образовавшиеся транспортные системы. Существование каждой клетки резонансно обеспечивается существованием всех остальных. Благодаря структурно-волновому резонансу биологические поля, создаваемые отдельными клетками усиливаются и синхронизируются, формируя биологический мультиполь. Тем самым открывается возможность для дальнейшего роста и развития возникшего организма. Однако, законы этого роста становятся другими. Сближение внутренних клеток уменьшает скорость их роста и резко увеличивает период между размножениями. Однако этот период не становится бесконечным. Происходит резонансная синхронизация периодов существования отдельной клетки и их совокупности, определяющая большой, но обязательно конечный период существования сформировавшегося единого организма (не здесь ли таится загадка жизни и смерти многоклеточных организмов?). Резонансное взаимодействие клеток с различными районами создаваемого ими биологического поля и возможность их участия в бифуркационных событиях приводит к их дифференциации. Особенно существенными оказываются различия между граничными клетками и внутренними. Граничные клетки обладают значительно большим числом степеней свободы, чем клетки, расположенные внутри объёма и      по своим характеристикам приближаются к недифференцированным клеткам свободно растущей популяции. Об этом свидетельствует недавно открытая возможность клонирования многоклеточных организмов не только с использованием стволовых (недифференцированных или слабо дифференцированных) клеток зародыша, но и клеток кожи животных. Внутреннее поле организма существенно неоднородно, и его интенсивность и структура определяется внутренней геометрией организма. Поэтому его структура резонансно определяет вид дифференциации клеток, что приводит к их синхронизации с динамикой всего организма и необратимости произошедших изменений.      Совершенно в других условиях находятся клетки поверхности. Воздействие на них собственного поля организма значительно слабее, частота их размножения выше. Они более подвижны и активны.

    Так как резонансные изменения внешнего поля, вызываемые синхронизированной группой клеток, значительно превышают интенсивность поля, индуцированного аналогичной группой свободно живущих клеток, то зона влияния сформировавшегося организма оказывается значительно выше. Граничные клетки могут формировать длинные нити, связанные с основной резонансной грибовидной структурой, и расположенные по силовым линиям нового биологического поля (ножки грибовидных структур), и в новых местах рождать новые грибовидные структуры, связанные с первичными. Разграничение свойств и функций клеток позволяет популяции строить два типа связанных между собой поселений: концентрированные «шляпки» грибовидных структур с плотным расположением клеток, создающих мощное резонансное биологическое поле, и нитевидные «ножки» грибовидных структур, охватывающие большие поверхности, площадь которых пропорциональна мощности этого поля. Нитевидные структуры служат для активного добывания пищи, а также для её транспортировки. Тем самым многоклеточные организмы благодаря сложным резонансным процессам вводят в свою структуру существенную дифференциацию, что приводит в конце концов к формированию не только нового организма, но и его собственного контроллера. Часть функций управляющего механизма отдельной клетки передаётся постепенно формирующемуся контроллеру многоклеточного организма. Почти хаотическое движение клеток в свободной биологической волне, имеющее большое число практически равноправных степеней свободы движения и роста каждой отдельной клетки переходит в относительно упорядоченное движение системы, в котором рост и движение каждой клетки резонансно синхронизировано с движением остальных клеток. В системе с необходимостью возникает внешний по отношению к отдельным клеткам гомеостатический контроллер, действующий путём трансформации биологического поля, например, путём синхронного электромагнитного взаимодействия отдельных клеток, или выработки химических веществ, синхронизирующих поведение отдельных клеток (зачаток эндокринной системы).

    Резонансное формирование многоклеточных структур явилось важнейшим шагом в развитии биосферы. С их формированием появились новые, макроскопические кванты живой материи, существование которых позволило регулировать скорость размножения и одновременно увеличить сферу существования живых организмов. Но главное, - возник принципиально новый, внеклеточный механизм управления совокупностями клеточных структур (гомеостатический контроллер организма). За счёт ограничения числа степеней свободы одной клетки организм приобрел большую вероятность для практически невозможных ранее степеней свободы на более высоком масштабном уровне.

    Некоторые основные закономерности резонансной самоорганизации клеточных популяций оказываются характерными и для социальных систем. В частности, события, происходящие в настоящее время внутри человеческого общества, связанные с демографическим переходом, во многом аналогичны описанным выше. Особенно явно это стало заметно после 80-х годов двадцатого века, когда окончился демографический взрыв и стали более интенсивно развиваться процессы самоорганизации человечества как единой системы (демографический переход). Резкое увеличение размеров и этажности городов, где люди живут почти вплотную друг к другу, во многом аналогично формированию грибовидной структуры слизневика. Всё в большей степени внешней средой для отдельного человека становятся другие люди, тесно с ним взаимодействующие, что приводит к необходимости создавать и совершенствовать транспортные системы для снабжения каждого человека необходимыми ему ресурсами. Всё более развивается единый обменный эквивалент – деньги, определяющий возникшие экономические взаимоотношения между людьми. В последние годы в связи с демографическим переходом значительные качественные изменения происходят и в экономике,  к изучению которой также может быть применена концепция вихре - волнового и структурного резонанса.

 Роль неоднородной среды в этом случае играет совокупность объектов и субъектов, между которыми осуществляются производственные и экономические отношения. Так как в экономике уже выработался естественный параметр целого - деньги, то их объём, выраженный в некотором эквиваленте, может считаться своеобразным геометрическим размером субъектов экономики. Количество денег, принадлежащих той или иной корпорации, может считаться её размером или длиной эквивалентной ей волны. В экономике постоянно происходит оборот денежной массы. Период обращения денежной массы того или иного субъекта экономики может считаться частотой эквивалентной волны, а её скоростью можно считать отношение денежной массы к периоду обращения.

Совокупность субъектов экономики обладает неким свойством, которое можно считать эквивалентным дисперсионному соотношению сплошной среды. Каждому субъекту экономической деятельности, успешному в данном поле, соответствует определённая связь между его объёмом и частотой оборота средств. Эта связь может быть экспериментально определена. Если появляется какой-либо новый участник экономической системы, то можно предположить, что его деятельность будет успешной, если его капитал и предполагаемая частота его оборота будут соответствовать дисперсионному соотношению экономической среды, в которой он собирается действовать. Однако указанное условие должно явиться необходимым, но не достаточным условием успеха.

Концепция вихре - волнового и (или) структурного резонанса может быть после соответствующей проверки использована и при выборе партнёров в экономической деятельности. Для выполнения необходимого условия структурного резонанса необходимо, чтобы партнёры имели близкие величины капитала и скорости его оборота. Если же взаимодействуют компании с различными объёмами капитала, то в более крупной компании должно быть самостоятельное подразделение, близкое по объёму капитала и скорости его оборота к меньшей из компаний [2].     

 

Литература

 

1. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144 с.

2. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с

3. Басин М.А., Шадрин В.П. Гидро-аэродинамика крыла вблизи границы раздела сред. Л. Судостроение. 1980. 258 с.

4. Хакен Г.Синергетика. М.: Мир. 1980. 414с.

5. Васильев В. А., Романовский Ю. М. , Яхно В. Г. Автоволновые процессы. М.: Наука. 1987. 240 с.

 

Часть  I.

Синергетика.

Информационно-волновая теория структур и систем.

 

Синергетика. Этюды 70.

Посвящено 100-летию со дня рождения выдающегося учёного, профессора

Басина Абрама Моисеевича.

Басина Г. И., Басин М. А.

НИЦ «Синергетика» Санкт-Петербургского союза учёных.

Этюд 35 

Об изучении сложных структур.

 

29 ноября 2009

 

Наиболее трудно поддаются научному исследованию сложные природные структуры и системы, состоящие из большого числа различных элементов, имеющие интенсивные внутренние связи, осуществляющие активный обмен веществом, энергией и информацией с внешней по отношению к ним средой.

Применять в лоб для анализа поведения таких структур методы математического анализа нецелесообразно, так как можно найти много параметров и даже попытаться написать уравнения для определения динамики их изменения. Однако, решать эти уравнения в  большинстве случаев нецелесообразно  не только потому, что не очень ясно , как обрабатывать полученное большое количество информации, а, в основном, потому, что никто заранее не гарантирует, что выбранные нами параметры (которых невообразимо много) именно те, которые описывают существенные особенности той структуры или системы, которую Вы изучаете, и неизвестно даже, правильно ли Вы выбрали саму структуру и объединили входящие в неё элементы.

Не поэтому ли считается, что для исследования таких сложных систем как человек, человеческое общество , биосфера, биологические объекты, культура и т.д., математические методы просто неприменимы. Недаром. науки, изучающие эти системы называют гуманитарными.

       При этом изучение более простых объектов поддаётся математическому описанию, и здесь наука и технологии достигли фантастических успехов, приведших в ХХ веке к научно-технической революции. Причиной этого является то, что гении человечества благодаря своему труду или благодаря глубокой интуиции сумели найти для этих явлений не только основные переменные, но и сравнительно простые фундаментальные уравнения, описывающие изменение этих переменных.

 Открытие уравнений Ньютона, а затем их модификация для микромира в виде квантовой механики и квантовой теории поля и для случая очень больших скоростей и геометрических размеров в виде общей теории относительности, а также успехи теории сплошной среды и статистической физики для объяснения широкого круга явлений неживой природы и многих биологических явлений породили у учёных в середине двадцатого века эйфорию всемогущества классических и неоклассических теорий. Эта эйфория подогревалась фундаментальными открытиями практически во всех областях знаний. Казалось, что основные уравнения динамики отдельных элементов систем любой природы в принципе могут быть решены численно, лишь бы иметь в своём распоряжении мощные расчётные устройства. И вот такие устройства появились и стали быстро и интенсивно развиваться. Их развитие продолжается и сейчас, перевернув всю жизнь человеческого общества так же, как это сделали до этого атомная бомба, радио, телевидение. Процесс мощного наступления вычислительных технологий продолжается и сейчас, хотя уже наблюдается некоторое  насыщение.

Однако уже сейчас очевидно, что все эти достижения, приводящие к резкому увеличению производительности труда , резко изменяя условия жизни человека,создают для человека всё новые и новые проблемы. Наука не решет всех человеческих проблем, а наоборот, ставит новые. Оказывается, что те уравнения, которые написаны и решаются учёными всё точнее и точнее на более мощных машинах, не решают извечных проблем человечества и не могут предсказать его будущего. Да и на вопрос, нужно ли решать эти уравнения, учёные дать ответа не могут. Кроме того, в самой науке и всей научной иерархии, работавшей в ХХ веке , в основном, на военно-промышленного комплекса произошли существенные структурные изменения, которые привели учёных в башню из слоновой кости, помещения которых очень тщательно изолированы друг от друга.

Что же делать?

1.      Синтез внутри науки

2.      Разработка на основе этого синтеза принципиально новых методов исследования структур и систем.

3.      Синтез науки с другими элементами человеческой культуры.

О новых методах исследования. Эти методы обязательно должны быть качественными.

По счастью, именно в конце двадцатого века наука, и в частности, математика, поставила на щит качественные методы исследования.

В чём они состоят?

Начнём с первого.

Выделение объекта из природы.

Этот вопрос является скорее гносеологическим, чем научным. К счастью, весь наш мир устроен так, что большинство объектов, с которыми мы имеем дело, таковы, что они имеют чётко выраженные границы в пространстве и во времени. Эти границы объективны и их объективность позволяет нам одни объекты от окружающего их мира от других. Выделение объекта – это первый, возможно, самый важный этап познания. Это первая степень абстракции. Следующий этап – название выделенного  объекта – то есть  придания модели этого объекта, сложившегося в нашем сознании словесного символа.

Если объект назван, мы уже начали его изучать. Название объекта –это уже введение простейшей группы 01 –да-нет. Объект может существовать-да 1 и не существовать-нет 0. Можно ввести групповые соотношения

0*1=0 –ликвидация объекта

1*0=1 – подтверждение отсутствия объекта

1*1=1  - подтверждение существования объекта

0*0=1 – рождение объекта.

Это коммутативная группа существования объекта.

Тем самым мы получили первое групповое соотношение существования- отсутствия объектов. Название дало нам очень многое. Такой подход вводит нас в стандартное понятие языка – язык это первый и наиболее важный метод изучения природы. Тут же  появляются и основ другого языка – языка математики, языка групп.

       Однако, уже на этом этапе  можно ввести ещё одно очень важное представление – представление о вероятности. Да, действительно, по-видимому, природа устроена так, что каким-то образом отделяет одну структуру от другой, один предмет от другого, имеется процесс становления и исчезновения предметов и явлений. Не всегда распознавание образов предметов и явлений является однозначным. Здесь лежат основы выхода в теорию вероятностей. Вообще (личное сообщение Э. А. Троппа) наше познание является обратной задачей, которая сама по себе всегда некорректна. И это нужно помнить. Триады Р. Г. Баранцева все асимптотики следуют именно отсюда.

Кроме того, здесь появляется первая триада

 

                                                                       Вероятность

                                                                    ./                        \

                                                        Существование Несуществование

Итак, мы  выделили изучаемую структуру , вели множество существования и ввели на этом множестве меру p . Далее мы построили на этом множестве групповую структуру – получили простейшую группу.

Таким образом, выделив из природы «словом» какой-то объект  мы, кроме этого «слова» -элемента языка, ввели сразу достаточно глубокую математику – понятия множества, вероятности (меры), группы. Так как эти понятия в математике являются фундаментальными, то их сразу можно применять при создании моделей объектов.

Далее этот первый шаг можно развивать по трём направлениям:

А)Экспериментальное исследование объекта при помощи своих органов чувств или любых других приборов, их развивающих и продолжающих.

Б) Словесное описание объекта исследования и его поведения.

В) Математическое описание объекта исследования –качественное и количественное.

Выделенный нами объект исследования обладает какими-либо существенными свойствами, которые мы различаем после того, как мы его выделили. Эти существенные свойства объекта исследования, так же, как и сам объект, могут быть названы человеком. Таким образом, мы можем экспериментально исследовать объект и его свойства. Первым и наиболее важным свойством объекта является его существование. Другие свойства также могут быть описаны словами. Например, физические объекты имеют геометрические размеры –длину, ширину, высоту. Каждому свойству, кроме слова, его описывающего приведём в соответствие  обобщённую координату, которая может быть обозначена. Таких координат может быть одна, если мы назвали объект и выбрали его параметр целого, либо много, либо так много, что их число можно считать бесконечным. Каждой обобщённой координате можно сопоставить шкалу величин. Если координата описывается словесно, то на шкалеона принимает только два значения 0 и 1. Она может принимать также дискретные и непрерывно меняющиеся значения. Наряду с изучаемым нами объектом возникает в нашем мозгу модель объекта, или иерархия связанных между собой моделей. Модели могут быть языковыми, математическими и физическими. Модель – это создаваемая человеком конструкция поведение которой,по мнению человека, аналогично исследуемому им объекту. Главный следующий шаг – это выбор основного  параметра (параметра целого). Возможность выбора именно одного расчётного параметра связана, по-видимому, с понятием «целостности системы, так же, как и её название. Если такой параметр может быть найден, то это косвенно свидетельствует о  единстве (целостности) системы. Этот параметр может изменяться . Для  описания этого изменения необходимо ввести аргумент, в зависимости от течения которого происходит изменение параметра целого.

Время имеет несколько ипостасей.

Рассмотрим две из них.

1)     Эйнштейновское время – это одна из обобщённых координат, во многом эквивалентная другим обобщённым координатам системы, ничем из них не выделенное. Такой подход к времени позволяет во многих случаях вносить дополнительную однородность в изучение системы.

2)     Ньютоновское время –параметр следования –его введение обязательно предполагает наличие наблюдателя – исследователя –внутреннего или внешнего, который движется вместе со структурой и фиксирует те или иные изменения   .

При рассмотрении систем первая ипостась времени характеризует его однородность и ненаправленность процессов во времени (отсюда –закон сохранения энергии). Вторая ипостась времени, наоборот , формирует стрелу времени и определяет различие между прошлым и будущим.

Введя одно только время (в смысле Ньютона –Бора) и не вводя никаких других параметров, мы можем, привлекая всё то, что уже говорили ранее, рассмотреть выделенный нами объект как динамическую систему.

На рис . 1 представлено простейшее детерминированное представление целостной структуры во времени.  До момента  структуры не существовало. Переменная, соответствующая данной целостной структуре, равнялась нулю. В момент  произошло рождение нашей структуры, которая просуществовала до момента , после которого она исчезает. Такое простейшее рассмотрение позволяет ввести ряд глубоких понятий.

1.      Момент рождения структуры .

2.      Момент разрушения (исчезновения) структуры .

3.      Срок жизни структуры .

Такое представление порождает графическое изображение, простейшую фазовую траекторию структуры во времени, в виде «шляпы».

Конечно, можно себе мыслить вечные структуры, но весь жизненный опыт подсказывает, что в рамках возможности введения понятия времени как параметра вечных структур нет. Вечность - это «нирвана» индусов. Поэтому в качестве аксиомы можно принять гипотезу о том, что все структуры имеют начало и конец во времени, то есть имеют некоторую длительность существования.

Введённые параметры порождают три проблемы.

1.      Что такое рождение структуры?

2.      Что такое разрушение структуры?

3.      Что такое время и как его измерять?

Остановимся первоначально на третьей проблеме. Для того, чтобы фиксировать изменения структуры во времени необходимо ввести в рассмотрение наблюдателя. Ведь именно наблюдатель способен строить модели и мысленно выделять объекты из природы. Для этого его органам чувств необходимо постоянное взаимодействие с окружающей средой. Последовательность взаимодействий порождает шкалу следующих друг за другом моментов – шкалу времени. Основное допущение Ньютона состоит в непрерывности, однородности и бесконечности абстрактного времени.

Такая гипотеза даёт в руки исследователя блестящее оружие – ось времени!!! Хотя мы не всегда можем фиксировать все происходящие события, но если мы фиксируем их дискретно, то предположение о гладкости и непрерывности даёт нам возможность аппроксимировать результаты проведённых измерений. Но наша «щляпа» построена в системе двух координат. Второй координатой в рассмотренном выше случае былиа совокупность чисел 0 и 1. Это простейший частный случай введения некоторой меры – параметра целого. В более общем случае мера –параметр целого может принимать как дискретные, так непрерывно меняюиеся значения как в области действительных, так и в области комплексных чисел. Предположим, что нам известен график зависимости меры, характеризующей структуру, построенный на основе экспериментальных данных или теоретических соображений. При этом параметр целого может быть нормализован по своему максимальному значению. Наиболее характерной характеристикой при исследовании физических объектов является их масса. Таким образом для описания объектов природы мы имеем как минимум две координаты , существенно отличающиеся друг от друга: время и параметр целого.

 

 

 

          Глава 1.

          Волновой подход к исследованию структур и систем.

           

     Основой для познания окружающего мира является наше с ним взаимодействие, в результате которого могут быть выделены отдельные объекты, а затем изучены их свойства. При выделении объекта из природы мы составляем в мозгу его образ, даем ему имя и вводим простейшую математическую группу, характеризующую отсутствие, рождение, существование и исчезновение объекта. Тем самым, мы используем три языка науки:

а) язык образов,

б) язык слов,

в) язык математики [1].

Язык образов позволяет получить наиболее общее представление о красоте и многообразии окружающего мира и о взаимодействии объектов между собой.

 Язык слов помогает отметить важную особенность природных явлений, позволяющую строить научную картину Природы, - существование объектов, во многом идентичных друг другу, которые могут быть названы одним словом.

 Язык математики позволяет уже на первой стадии рассмотрения ввести простейшую математическую группу, характеризующую возникновение, существование и исчезновение объекта, а также считать количество идентичных объектов.

Математическим отображением динамики структуры или системы может являться последовательность отображений абстрактных множеств  с определёнными на них комплексными функциями, квадрат модуля которых определяет вероятностную меру на этих множествах. В частности, в качестве пространства возможных состояний системы (вероятностного пространства) во многих случаях может быть принято либо дискретное множество, либо многомерное дифференцируемое многообразие. Изменение во времени распределения вероятности того, что система окажется в той или иной точке этого пространства, характеризует динамику  вероятностной волны, соответствующей данной системе.

Структурная часть комплексной функции представляется в виде комплексного множителя с единичным модулем, показателем мнимой экспоненты которого является отношение зависящей от времени меры (действия) структуры к некоторому масштабному коэффициенту (аналогичному постоянной Планка).

 Для сложных структур и систем в некоторых случаях действие структуры может рассматриваться также как действительная мера, определенная на внутреннем структурном множестве (многообразии). При этом существенную роль играет проблема выбора внутренних обобщенных координат, характеризующих структуру или систему.

Первым вопросом, возникающим при исследовании сложных структур и систем является вопрос о связи между пространством, описывающим возможные состояния структуры,  внутренним пространством структуры как сложного объекта и внешним геометрическим пространством, описывающим геометрию окружающей среды (поля) . Постановка этого вопроса указывает на ещё один волновой аспект динамики сложных структур и систем - проблему идентификации вероятностного,  структурного и геометрического пространств, в рамках которых описывается система, приводящий к определению таких понятий как квант, обобщённая волна и поле.

Вторым вопросом, возникающим при исследовании сложных структур и систем, является проблема выбора обобщенных координат пространств, в рамках которых описывается динамика структуры и (или) системы - то есть основных координат, характеризующих внутреннюю структуру системы, а также координат, описывающих совокупность возможных состояний системы  и динамику перемещения структуры относительно поля.

Третьей проблемой  является проблема времени . Входит ли время (времена) – в число обобщенных координат, описывающих динамику структуры или системы, или оно является параметром, связывающим последовательные отображения абстрактных множеств, соответствующих различным состояниям структуры? Время имеет, как минимум, две ипостаси:

a)    время как параметр, изменяя который мы следим за изменением структур (систем ) и полей;

б)  время как одна из обобщенных координат.

Одной из важнейших проблем синергетики и науки вообще является проблема обратимости времени. В настоящее время становится очевидным, что частичное решение этой проблемы связано с процессами потери устойчивости, бифуркационными процессами, процессами перезамыкания границ, формированием ударных волн, хаотизацией.

Другой философской и математической проблемой, связанной со временем, является проблема его дискретности и непрерывности и возможностей перехода от его дискретного введения к непрерывному.

 

 

Глава 2.

Граф структур и событий.

.

 

Событие.

Мир состоит из взаимодействующих между собой структур и систем, которые с той или иной степенью достоверности могут быть выделены из окружающей среды. Простейшей математической моделью эволюции систем является граф, одной из координат которого является время. Узел эволюционного графа с малыми отрезками прилегающих к нему ребер, соответствующий определенному критическому моменту эволюции будем называть событием. Естественная классификация графов и соответствующих им свободных групп может служить основой классификации типов ветвей мировой эволюции [3].

Во многих случаях внешнее проявление взаимодействующих структур или систем кажется нам детерминированным: состояния систем до момента взаимодействия  практически полностью определяют их состояния после взаимодействия, то есть после свершения события [4].

Однако объекты природы, иногда проявляют свою свободу при взаимодействии между собой или при внутренних трансформациях. В этом случае исход события не может быть предсказан однозначно. Поэтому для адекватного отражения реального мира эволюционный граф должен иметь еще одну координату - бифуркационную. Мир устроен таким образом, что предсказать исход того или иного события не всегда представляется возможным .

Бифуркационные события. Пусть имеются две исходные структуры. Можем ли мы заранее знать, что произойдет в результате взаимодействия? Будет ли результат однозначным? Вовсе не всегда повторение казалось бы одинаковых опытов приводит к однозначному результату. События, результаты которых не могут быть однозначно предсказаны, будем называть бифуркационными событиями [6].

     Каждому будущему бифуркационному событию соответствует не один, а несколько результатов, которые могут реализоваться  после свершения события. Эти результаты образуют множество возможных результатов данного события. Если событие произошло, то из всего множества возможных результатов реализуется один, и дальнейшее развитие процесса происходит лишь по одному из возможных сценариев до тех пор, пока не произойдет новое событие с несколькими возможными исходами.

Таким образом формируется бифуркационная размерность графа структур и событий. При этом каждый вариант результатов взаимодействия может иметь свое количество результирующих структур.

Зная предшествующее событию состояние системы, время свершения события и возможные его исходы, можно построить любое структурно- бифуркационное сечение будущего.

С другой стороны, если взаимодействующие структуры рассматривать как единую динамическую систему, то

бифуркационное событие - это такая качественная трансформация параметров системы, которая может вывести на несколько различных аттракторов.

Перевязка аттракторной и вероятностной интерпретаций исходов бифуркационного события даёт путеводную нить к выяснению механизмов многозначности результатов почти идентичных  событий.

Будущее известно лишь с какой-то вероятностью. Изучение законов природы позволяет лишь снизить до минимума  неопределенность в этом знании. Однако, будущее может через некоторое время стать настоящим и, если считать, что о настоящем известно больше, чем о будущем, то принципиально всегда можно уменьшить неизвестность будущего до какой-то минимальной величины, сделав его настоящим, после чего оно становится прошлым, и вновь неизвестным, но по-иному. Тем самым путём идентификации будущего и настоящего мы получаем информацию об исходе бифуркационного события.

Однако аттракторный подход к исследованию бифуркационных событий позволяет рассматривать и события противоположного типа. В некоторых случаях различные события или цепочки событий могут привести к одному аттрактору - некоторому событию с одним исходом. Здесь скрыт ещё один из механизмов формирования информации за счёт идентификации исходов событий.

Именно наличие таких аттракторов и возможность их предсказания позволяет сложным структурам и системам выживать в хаосе бифуркационных событий.

В нашей  монографии [6] и других исследованиях введен ряд новых понятий.

-       По аналогии с квантовой механикой [8], – комплексный волновой вектор бифуркационного события.

-       Мера, характеризующая совокупность взаимодействующих структур и соответствующий ей оператор.

-       Обобщенный параметр Планка, характеризующий цикличность влияния меры на комплексный волновой вектор бифуркационного события или цепочки событий.

-       Комплексный оператор «действие - энтропия» произвольного сечения графа структур и событий.

-       Энтропия будущего бифуркационного события и цепочки бифуркационных событий как мера неопределённости, связанная с возможностью существования нескольких альтернативных исходов.

-       Информация, приобретаемая при свершении события в результате идентификации одного из возможных исходов с реальным исходом произошедшего события.

-       Информация, приобретаемая при идентификации нескольких возможных исходов события или цепочки возможных событий.

-       Информация, приобретаемая в результате идентификации исходов будущего события с исходами аналогичных событий, произошедших в прошлом с данной структурой

-       Информация, приобретаемая в результате идентификации исходов будущего события с исходами аналогичных событий, произошедших со структурами, аналогичными данной.

-       Энтропия прошлого.

-       Память о событиях, которые приводят к данному состоянию.

-       Волновой вектор-матрица системы взаимодействующих структур.

В случае, если мера, определяющая динамику структуры, значительно меньше значений, принимаемых параметром Планка, то разрабатываемая теория становится аналогичной классической теории случайных процессов и теории динамических систем, сохраняющих меру.

Введенные понятия и соответствующие им математические структуры позволили получить ряд аналитических соотношений для параметров бифуркационного события или цепочки бифуркационных событий.

Среди них:

     формулы для векторного сложения комплексных компонент волнового вектора в случае идентификации исходов бифуркационного события или цепочки событий;

-        обобщенное равенство Шрёдингера для производной по времени от волнового вектора – матрицы;

-       обобщённое равенство Шрёдингера для производной по времени от комплексной волновой функции системы.

-       структурная формула для определения действия и энтропии-информации сложной иерархической системы, участвующей в бифуркационном событии.

-       обобщённый закон роста энтропии в системах, структуры, входяшие в которые, и события, происходящие с которыми, не могут быть идентифицированы.

Введены понятия комплексного оператора энергии и комплексной энергии системы, участвующей в бифуркационных событиях.

Доказана теорема о возможности расщепления вектора-матрицы произвольной системы на бифуркационную и структурную части.

Изучены некоторые частные случаи бифуркационных событий и цепочек событий, соответствующих отдельным ветвям графа.

 

Глава 3. Математическое описание изолированной структуры.

 

Математическое моделирование самоорганизующихся структур и систем начато с простейшего случая, который легко реализуется  на компьютере.

     Введено понятие автономной динамической структуры с конечным числом возможных состояний. 

Переход из одного момента времени в другой характеризуется некоторым  многозначным отображением одного состояния в другие. В рамках этого отображения переход из одного возможного состояния в другое, определяемый функцией, осуществляющей это отображение, характеризуется некоторым числом, которое будем называть вероятностью перехода. Тогда, если каждому моменту внутреннего времени сопоставить некоторое распределение вероятностей возможных состояний, то соответствующее распределение вероятностей состояний системы можно определить в любой другой момент времени как в прошлом, так и в будущем. Такая бифуркационная система названа автономной. Для этой системы, в случае конечного числа возможных состояний, может быть построен наложенный на собственное время граф бифуркационных событий с соответствующими этим событиям относительными вероятностями. Тем самым, вводится автономный вектор вероятности состояний, изменяющийся по наперед заданному закону, определяемому не зависящей от местного времени матрицей перехода.

Изучение свойств таких систем эквивалентно изучению свойств одного из частных случаев марковских процессов [9].

Рассмотрены частные случаи автономных бифуркационных систем с конечным числом возможных состояний и осуществлена их классификация.

Изучение динамики модели бифуркационной системы с конечным числом возможных состояний позволяет предложить её в качестве основного элемента нового типа компьютера, который мы назвали целостным.

Такой компьютер должен включать в себя триаду элементов, являющихся, как это было показано нами в [6], необходимыми составляющими любой самоорганизующейся транспортно-информационной системы.

 

Поле

/        \

                                   Собственно структура  ----- Контроллер

 

Целостный компьютер должен иметь квазифрактальную структуру - целостными должны быть не только компьютер, но и его элементы, а также иерархия его подсистем и систем, которые формируются из компьютеров этого типа.

Собственно структурой целостного элемента такого компьютера может стать бифуркационный элемент - компьютерная реализация динамики автономной бифуркационной системы с двумя возможными состояниями.

Контроллером элемента целостного компьютера является внутренний механизм, вырабатывающий значение величины распределения вероятности между двумя состояниями элемента.

Кроме того, должен существовать генератор действительных чисел, который может моделировать поле элемента.

Перечислим некоторые из задач, которые могут быть решены при помощи целостного компьютера.

5.    Математическое моделирование стохастических процессов, в частности, марковских цепей.

6.    Описание цепочки бифуркационных событий, при реализации каждого из которых компьютер может с определенной вероятностью выйти на некоторый детерминированный алгоритм, завершающийся очередным бифуркационным событием. Тем самым возникает возможность создания компьютерной модели бифуркационного процесса.

7.    Моделирование некоторых аспектов самоорганизации сложных динамических систем (например, режимов самоорганизованной критичности).

8.    Изучение динамики размножающихся систем и процессов.

5. Анализ генезиса устойчивых статистических распределений  в транспортно-информационных системах, а также моделирование явления эволюции реальных структур и систем.

Если ввести в рассмотрение внешнее время как непрерывно изменяющийся параметр, то всякая автономная структура, несмотря на потенциальную бесконечность, имеет начало и конец, а следовательно, какой-то период существования и тем самым отличается от рассмотренной выше идеальной модели, имеющей потенциально бесконечное время существования.

Простейший, наиболее схематический вид описания этого свойства реальных структур  состоит в представлении динамики структуры в виде двух чисел 0 и 1,  где 0 соответствует отсутствию структуры, а 1 - ее существованию. До момента  структуры не существовало. Мера  существования  заданной структуры, равнялась нулю. В момент  произошло рождение структуры, которая просуществовала до момента времени , после которого она исчезла. Даже такое простейшее рассмотрение позволяет ввести ряд понятий.

 

1. Момент рождения структуры .

2. Момент разрушения - исчезновения структуры .

3. Срок жизни структуры  .

 

Если процесс существования структур рассматривать как непрерывный во времени, то в моменты возникновения и разрушения структур в природе должны происходить качественные изменения (ведь рождается (или исчезает) нечто существенное). При простейшем рассмотрении можно считать, что рождение и исчезновение структуры происходят мгновенно. Это достаточно сильное допущение, хотя во многих случаях действительно происходит очень быстрое формирование новых структур и разрушение старых. Не зря в человеческом языке существуют такие слова, как катастрофа, кризис, взрыв, революция и т.д. Однако, как бы быстро ни происходило в некоторых случаях формирование новых структур, всё равно это процесс, имеющий ту или иную протяжённость во времени. В некоторых случаях процесс формирования структур может оказаться достаточно длительным. Какие же изменения в рассмотренном нами подходе можно ввести, если учесть указанные обстоятельства? Вместо мгновенного формирования структуры и мгновенного её разрушения необходимо ввести какие-то конечные периоды возникновения и разрушения структуры. Это вполне естественное допущение влечёт за собой ряд следствий.

Первое следствие состоит в том, что возникает вопрос, а что же происходит со структурой в эти периоды? Существует она или нет? Ответ на этот вопрос совсем не тривиален. По-видимому, в периоды рождения и разрушения про структуру нельзя с полной определённостью сказать ни то, что она существует, ни то, что её нет. Если всё же считать процесс формирования структуры непрерывным и в момент структура отсутствует- 0, а в момент  структура существует-1, то точки траектории структуры на временном отрезке , можно соединить плавной кривой. Значения величин функции, описываемой этой кривой, можно интерпретировать как меру существования (зрелости) структуры. В период рождения нельзя сказать, что структура не существует, но ещё нельзя сказать что структура уже полностью оформлена.

 Попытаемся решить эту задачу с другой стороны. Мера, характеризующая произвольную структуру, может быть получена, например, как объём многообразия, определяемого обобщёнными координатами внутреннего пространства. Этот объём может меняться в процессе существования структуры. Если структуры нет, то нет и многообразия, ее описывающего. В процессе существования (функционирования) структуры существует какой-то промежуток времени, когда многообразие, описывающее структуру, имеет максимальный объём. Если объём многообразия, описывающего структуру в любой момент времени, поделить на его максимальное значение, то получим в наиболее естественном случае некоторую кривую зависимости этой относительной величины от времени, начинающуюся с нуля и плавно выходящую на единицу.

     Рассмотрим некоторые общие закономерности, связанные с этапом рождения структуры. Как следует из той информации, которую мы получаем при изучении природы, можно рассматривать несколько способов рождения новых структур.

а) Появление новой структуры (волны) вследствие объединения или самоорганизации нескольких однородных структур (квантов).

б) Появление новой структуры в результате деления структуры на две и более частей.

в) Появление новой структуры или нескольких новых структур вследствие потери устойчивости структуры, существовавшей до их образования

г) Рождение новой структуры в результате полного или частичного слияния двух родственных структур с возможным переходом затем к многократному использованию  второго способа.

д) Рождение новой структуры путем излучения структур более высоких классов.

е) В качестве отдельного способа может рассматриваться целенаправленное формирование новых структур структурами более высокого класса.

Способы рождение новых структур в биологии описаны, например, П. Тейьяром де Шарденом.[10,с. 90].

Большинство описанных способов  приводит к необходимости анализа процесса формирования новых структур как бифуркационного изменения старых, уже существовавших ранее систем и структур . Тем самым, процесс появления и разрушения структур включается в цепочку превращений одних структур в другие [6].

Во многих случаях мы считаем, что структуры после своего появления начинают изменять значения обобщённых координат, не меняя, например, числа обобщённых координат приближенно описывающего их многообразия.  В качестве примеров можно привести:

а) рост амплитуды поверхностной морской волны при приближении её к берегу;

б) рост парового пузырька или паровой каверны при увеличении скорости движения тела;

в) рост кристаллов в растворе;

г) рост атомного гриба;

д) рост живого организма;

е) рост числа научных исследований в новой отрасли знаний.

Процессы такого роста могут значительно отличаться друг от друга, однако во многих случаях они обладают некоторыми общими особенностями. Если для структур такого типа может быть введён какой-либо один параметр, интегрально определяющий меру структуры (параметр цeлого), то в некоторых случаях можно не только выделить общий механизм формирования таких структур, но и найти простейшие математические модели, которые приближенно описывают этот механизм и которые позволяют моделировать количественные и качественные закономерности роста структур в данном случае.

В [6] показано, что при анализе динамических структур и систем можно ввести комплексную волновую функцию (вектор-матрицу), описывающую динамическую систему (структуру), реальная и мнимая части которой связаны с мерой, характеризующей её внутреннее фазовое пространство и вероятностными характеристиками бифуркационных событий, в которых структура участвует.

     Эти обстоятельства позволяют рассматривать в качестве математической основы для  исследования структур на первом этапе цепочку голоморфных функций комплексной переменной [11]. Эта переменная может быть названа комплексным параметром целого структуры (или комплексным параметром Планка).

В соответствии с высказанной гипотезой на следующем шаге рассмотрения в качестве области определения комплексной меры, описывающей возможные совокупности состояний, в которых может находиться динамическая система, принято поле комплексных чисел (поле действительных чисел рассматривается как частный случай этой более общей области рассмотрения ).

Подробно исследована цепочка линейных отображений комплексного переменного, и изучены характерные особенности этой динамической системы. Показано, что при определённых условиях в пределе большой частоты итераций динамика такой системы становится эквивалентной динамике, описываемой комплексным линейным дифференциальным уравнением. Получено общее решение этого уравнения в виде экспоненциальной функции от времени. Возможна такая интерпретация природных явлений, что обычное внешнее время - время взаимодействия  является лишь линейным приближением к реальному (экспоненциальному) времени динамической структуры (касательной к экспоненциальной кривой в единице). Тогда реальным временем, определяющим динамику структуры, может явиться не линейное время, а экспоненциальное время. В этом случае главную роль в анализе динамики структур играют не экспоненциальные, а степенные функции. Вполне возможно, что это частично объясняет вездесущность степенных функций при изучении самоорганизующихся структур.

Аналогичный подход к волновой функции позволяет ввести в рассмотрение экспоненты от степенных функций, общие свойства которых и возможные области их применения в настоящее время ещё мало изучены.

Замена параметров времени и волновой функции позволила осуществить цепочку трансформаций линейной системы [12]. В данном частном случае проявилось основное структурное свойство математических моделей (а следовательно, и структуры природных объектов, которые они описывают). Если применить к математическим исследованиям основную триаду Р.Г.Баранцева [13-18 ]

 

                                                    Интуицио

                                               /               \

                                        Рацио -------- Эмоцио,

 

то она может быть отображена на некоторое трёхмерное абстрактное пространство, обобщёнными координатами которого являются

                                         

 

                                       Континуальность

                                             (Мощность)

                                          /                           \

                             Размерность ---------- Иерархия

                     (Число переменных)    (Степень нелинейности)

 

Рассмотрим первоначально движение по оси континуальности.

     В начале этой оси можно расположить числа 0 и 1, связь которых с реальными объектами была установлена нами ранее. Следующими на этой шкале располагаются конечные множества (которые могут быть взаимно однозначно отображены на конечную совокупность целых чисел). Далее на шкале континуальности расположены счетные бесконечные множества (натуральный ряд чисел, бесконечные последовательности, совокупность рациональных чисел и т. д.). Ещё далее множества, обладающие мощностью континуума (иррациональные числа, действительные числа, комплексные числа, конечномерные матрицы и т.д.). Дальнейшее продолжение шкалы лежит в области определения мощности совокупности подмножеств множества мощности континуума [19]. 

Аналогичным образом можно перемещаться по оси размерности. Размерность – понятие, характеризующее число одновременно рассматриваемых переменных. Величина размерности может пробегать ту же совокупность значений, что и величина континуальности – от нуля и единицы до континуального множества координат, и, возможно, далее .

Анализ иерархической координаты математики начнем с линейных отображений. Линейная функция может быть определена на любой точке плоскости, формируемой двумя первыми координатами: мощностью и размерностью. Однако, уже анализ цепочек линейных отображений, подобный кратко описанному нами ранее для множества комплексных чисел выводит на следующий уровень иерархии. Цепочка линейных отображений, определяемых заданной функцией, порождает некоторый процесс, являющийся моделью потенциально бесконечной структуры. Эта последовательность порождает новый, сначала дискретный (принимающий последовательно целые значения) параметр времени, который при помощи предположения о гладкости рассматриваемых функций может быть преобразован в континуальный параметр. На этом уровне в математике появляются системы линейных дифференциальных уравнений, решениями которых оказываются экспоненциальные отображения. Этот процесс, с теми или иными особенностями, происходит над всей плоскостью континуальность - размерность и именно его изучению посвящена большая часть математических исследований.

Второй этаж иерархии формируется из первого путем взятия обобщенных экспонент от линейных операторов, действующих на первом этаже. Аналогично, переход от второго этажа к первому можно рассматривать как обобщённое логарифмирование функций и операторов, действующих на втором этаже.

Операции, выполненные нами при выводе степенных дифференциальных уравнений первого порядка, указывают на возможность рассмотрения связи между собой функций, находящихся на втором уровне иерархии. Эта связь - степенная. В этом случае мы оказываемся в области математики, которая названа А. Д. Брюно [20] степенной геометрией, включающей в себя в качестве частных случаев ряд интенсивно развивающихся в настоящее время разделов современной математики. Изучение конечных сумм и интегралов по показателям степени от степенных мономов одной или многих действительных и комплексных переменных представляет собой проблему, далеко не исчерпанную современной математикой (смотри, например, [11], [20], [21], [22], [23], [24], [4], [25], [26], [27], [28], [29], [31]). Уже на этом уровне, особенно при анализе функций с комплексными показателями степени, появляются многозначные (и даже бесконечнозначные ) отображения, лежащие пока ещё вне основной магистрали математических исследований.

Особую роль в классических исследованиях играют полиномиальные функции, которые, являясь частным случаем степенных полиномов, аппроксимируют гладкие многообразия. Именно в анализе полиномиальных функций нескольких переменных лежат основы теории особенностей гладких отображений и теории  катастроф [21], [25-29].

Однако, произвольные степенные функции и соответствующие им дифференциальные уравнения начали изучаться сравнительно недавно [20], хотя  многочисленные примеры исследования динамики нелинейных процессов, происходящих в самоорганизующихся структурах и транспортно-информационных системах свидетельствуют о том, что степенные функции встречаются повсеместно [20], [31], [32], [33], [77].

В связи с развитием голоморфной динамики [11], теории множеств Жюлиа и Фату [25], фрактальной геометрии [27] начались интенсивные исследования в области перехода со второго этажа на третий, где многозначность функций, графы, дробная размерность, вероятность реализации того или иного значения функции оказываются наиболее существенными особенностями исследуемых объектов. Вся интенсивно развивающаяся теория случайных процессов также относится к третьему уровню иерархии. Именно на третьем уровне иерархии исследователей ждут неожиданности и открытия.

При исследовании динамики комплексного параметра целого нами введена одна из возможных модификаций комплексных чисел, использование которой позволяет, если это необходимо, рассматривать степенные функции комплексного переменного с комплексными показателями степени как однозначные функции, а следовательно, применить к их исследованию аппарат функционального анализа [32].

Выполненные исследования позволили, в частном случае, построить цепочку связанных между собой комплексных математических моделей динамики размножения и роста живых субъектов, начиная от изолированной клетки и кончая популяцией организмов, в частности, человеческой популяцией, подробности построения которой изложены в четвёртой главе второй части настоящей монографии. Сделана первая попытка идентификации реальной и мнимой частей комплексного параметра целого [6 ] человеческой популяции как целостной системы.

 

Глава 4. Классификация волн, вихрей, структур и систем.

 

Мера, описывающая  детерминированную систему или систему, участвующую в бифуркационных процессах, в промежутках между бифуркационными событиями, обычно бывает распределена по некоторому внутреннему многообразию, размерность которого определяется числом обобщённых координат, которые приняты для описания внутренней динамики системы. Аналогично может выглядеть также описание динамики структуры в вероятностном пространстве. Поэтому в современной теории динамических систем часто рассматривают динамику автономной структуры как движение точки гладкого многообразия определяемого конечным (или бесконечным) числом переменных.[38], [28 ], [29]. Переменные , (). описывают изменение обобщенных координат, где  может быть одной переменной, но может являться некоторой совокупностью конечного или бесконечного числа переменных (как действительных, так и комплексных). Эти переменные формируют вектор состояния .

Внешняя динамика системы, как и в дискретном случае и в случае одной комплексной переменной, рассмотренных нами ранее, для детерминированных систем определяется изменением вектора состояния  системы во времени.

В большинстве интересных случаев в первом приближении состояние изучаемого объекта в тот или иной момент времени может быть задано точкой в некотором измеримом множестве , в частности , в - мерном многообразии. В этом случае говорят, что изучаемому объекту соответствует некоторая -мерная динамическая система, а множество всех точек, соответствующих различным состояниям называется - мерным фазовым пространством. Введём, как и ранее, в рассмотренных выше частных случаях, понятие состояния системы , под которым понимается значение вектора  в момент времени . Если предполагать время непрерывным, то совокупность состояний данной системы в различные моменты времени формирует линию, называемую фазовой траекторией системы. Если фазовое пространство системы -- мерное гладкое многообразие, то фазовая траектория системы - гладкая кривая и для ее описания (а также для описания пучка траекторий, начинающихся из различных точек фазового пространства) может быть использовано соотношение [29]

Частным случаем такого описания является система  дифференциальных уравнений.

Одним из наиболее простых случаев динамической системы является гармонический осциллятор, фазовое пространство которого двумерно. Фазовая плоскость колебательной системы описывается эллипсами. В действительности, в большинстве практически встречающихся устойчивых макроскопических систем обычно имеется диссипация, связанная с существованием неучтённых идеальной моделью обобщённых параметров, и поэтому фазовая траектория таких систем по спирали стремится к положению равновесия. Устойчивое положение равновесия системы является простейшим примером аттрактора динамической системы с континуальным фазовым пространством. Аттрактором является также устойчивый предельный цикл, соответствующий автоколебательному движению системы. Аттрактором может быть и гладкий тор. Аттрактор называется странным, если он отличается от конечного объединения гладких многообразий

Динамика детерминированных конечномерных систем в настоящее время развивается бурными темпами, изучаются все более сложные типы аттракторов и их бифуркационные трансформации как в действительных, так и комплексных многообразиях [2], [7], [11], [20], [24], [25], [26]-[29], [51-53].

Следующим этапом является исследование бесконечномерных волновых движений, динамических структур и транспортно-информационных систем.

Существует ряд учебников и монографий, посвященных результатам теоретических исследований волновых движений [39-48]. Однако, в большинстве из них отсутствует определение понятия "волна". Наиболее общее из известных нам определение волны дано в монографии [46]: "...в самом  общем случае мы определим волну как пространственно-временную эволюцию некоторого состояния." Это определение характеризует основное свойство волны, которое остается неизменным, независимо от типов волн, которые мы рассматриваем, а именно то, что при описании волновых движений мы следим не за частицами среды, в которой распространяется волна, а за параметрами или совокупностью параметров, которые описывают состояние среды, и которые остаются постоянными или слабо меняются в точках, которые мы считаем принадлежащими к волне.

Это общее определение явилось следствием интенсивного развития в последнее время исследований нелинейных явлений в различных областях знаний и обнаружения волновых свойств у таких нелинейных процессов и структур, которые ранее не считались волновыми. В [43.C.9] говорится: "Отечественная школа нелинейных колебаний и волн, основоположником которой по праву считается Л. И. Мандельштам, рассматривает общую теорию структур в неравновесных средах как естественное развитие и обобщение на распределенные системы идей и подхода классической теории нелинейных колебаний. Еще в 30-х годах Л. И. Мандельштам сформулировал программу создания нелинейной культуры, включающей надежный математический аппарат и физические представления, адекватные новым задачам, нелинейную интуицию, выработанную на нелинейных задачах". Там же указано, что Л. И. Мандельштам предупреждал о ненужности на определённом этапе исследований строгих определений всех понятий в нелинейной науке. Мы полностью присоединяемся к его мнению и считаем, что в настоящее время пока нет необходимости в абсолютно точном определении понятия "волна" (так же как и понятия структура. система, процесс, явление, событие). В последние годы исследования нелинейных процессов привели к зарождению и развитию новой науки-синергетики [7], [43-44],[49], [50] - науки о самоорганизации материи. Как показали многочисленные исследования, при изучении вопросов, связанных с формированием новых структур, на первый план выступают их характерные волновые черты: независимость их пространственных и временных параметров от начальных условий и геометрических размеров системы.

В рамках синергетической парадигмы нами предложена классификация волновых движений, структур и систем, опирающаяся на их общие волновые свойства, в рамках которой удалось проследить за характером влияния нелинейности на переход классических линейных волновых движений в динамические структуры и сложные самоорганизующиеся транспортно-информационные системы [54-60]. Тем самым сделан первый шаг к исследованию классификационной координаты мирового графа.

В качестве первого класса рассматриваются все волны относительно малой амплитуды, математическое описание которых может быть дано в виде совокупности решений линейных волновых уравнений в частных производных.

Ко второму классу, названному умеренно-нелинейными волнами, отнесены различные формы ударных волн в сплошных средах, солитоны, а также скачки тех или иных параметров в однородной среде и границы раздела сред. Особым подклассом умеренно-нелинейных волн могут считаться режимы с обострением, подробно изученные школой А.А. Самарского - С.П. Курдюмова [31].

К третьему классу, названному вихревыми ударными волнами, отнесены вихревые структуры, формируемые в районе фронта умеренно нелинейных волн. На основании анализа экспериментальных исследований формирования вихревых структур, решения ряда модельных задач и определения условий самопересечения волновых фронтов и границ удалось установить основные закономерности трансформации умеренно-нелинейных волн в вихревые структуры [61-62].

Пространственность взаимодействия линейных волн и волновых фронтов приводит также к возникновению «каустик», районов значительного увеличения их амплитуды. Классификация каустик, как показано В.И. Арнольдом и другими исследователями, сродни классификации особенностей гладких отображений [63], что возвращает к специфике динамических систем с конечным числом степеней свободы.

Наряду с этим потеря устойчивости волнового фронта может в особых самоподдерживающихся критических условиях приводить к множественному формированию структур различной природы, масштаб которых значительно меньше масштаба потерявшего устойчивость волнового фронта. Такой режим, названный режимом самоорганизованной критичности, в настоящее время интенсивно изучается. Статистические распределения масштабов формирующихся при этом структур часто имеют степенной характер [29].

Несмотря на то, что сформировавшиеся в условиях самоорганизованной критичности структуры могут представлять собой волны или структуры более низких классов сложности, сам процесс самоорганизованной критичности обладает некоторыми особенностями, присущими пятому классу предлагаемой нами классификации – транспортно-информационным системам.

К четвертому классу, названному грибовидными структурами, отнесены структуры мультипольной природы, формирующиеся  из вихревых структур и вторичных умеренно-нелинейных волн – вихревых пелен. Различные модификации и комбинации структур такого типа составляют основу практически всех объектов живой и неживой природы.

К пятому классу отнесены сложные самоорганизующиеся системы, названные нами транспортно-информационными  и являющиеся, в основном, результатом трансформации и взаимодействия грибовидных структур [60].

Несмотря на то, что четвертый и пятый классы структур и систем встречаются и в неживой природе, наиболее широко они распространены в биологических субъектах. Поэтому общие закономерности их динамики оказываются важными не только для физики и химии, но и, главным образом, для биологии и наук о человеке и обществе [64].

 

Глава 5. Вихре - волновой резонанс.

 

Предложенная классификация и связанные с ней новые теоретические модели позволили объяснить ряд новых физических явлений, обнаруженных экспериментально и теоретически при исследовании движения несимметричных тел в сплошной среде, как резонансное волновое взаимодействие вихревых и грибовидных структур с диспергирующими волнами, возникающими при их движении.

В последние годы было открыто  и широко исследовано резонансное взаимодействие поверхностных и внутренних гравитационных волновых движений [65].

Автором была высказана гипотеза о возможности возникновения аналогичных резонансных явлений при взаимодействии свободных вихрей и  грибовидных структур, а также газовых каверн, формирующихся при движении тел в неоднородной сплошной среде (поле), с диспергирующими внутренними волнами и другими типами волновых движений.

При теоретическом обосновании предложенной гипотезы была использована изложенная выше классификация волн, вихрей, структур и систем, на основе которой были определены необходимые условия резонанса, названного нами вихре-волновым (или структурно-волновым), состоящие в том, что скорости и размеры взаимодействующих структур должны быть близки. Теоретические расчеты и экспериментальные исследования частных проявлений вихре-волнового резонанса подтвердили высказанную гипотезу [12], [66-70].

Экспериментально и теоретически вихре-волновой резонанс исследовался при движении в неоднородной среде несимметрично обтекаемых тел – крыльев. В этом случае возникают две вихре-волновые структуры:

a)    вихревой пограничный слой на поверхности крыла  и вихревой след за ним;

b)     диспергирующие поверхностные и внутренние волны в неоднородной среде.

Проблема их взаимодействия частично поддается математическому моделированию. Результаты расчетов, полученные  при теоретическом исследовании взаимодействия возникающих вблизи крыла вихревых структур с возбуждаемыми его движением присоединенными внутренними и поверхностными волнами в режиме движения, который предполагался резонансным, показали, что даже при установившемся движении крыла в неоднородной среде, если длина хорды крыла близка к полудлине присоединенной к движущемуся крылу гравитационной волны, то в потоке жидкости или газа должны возникать аномальные возмущения. Эксперименты с крыльями, движущимися вблизи свободной поверхности воды, показали, что в этом случае на границе раздела сред возникают интенсивные возмущения, приводящие к разрушению волн и формированию вихревых структур, а силы, действующие на поверхность крыла, изменяются аномальным образом. Основным безразмерным параметром, определяющим вихре- волновой резонанс, в случае движения крыла вблизи свободной поверхности воды, является число Фруда , где - скорость движения; - длина тела. Если этот параметр находится в диапазоне , то в потоке наблюдаются проявления резонансного взаимодействия вихревых и волновых движений.

Как показали теоретические расчеты, в случае произвольной стратификации жидкости  (где -плотность нижней жидкости или газа, в которой движется тело, -плотность верхней жидкости или газа),  резонанс появляется при скоростях и размерах движущихся тел, которые соответствуют тому же числовому диапазону, но для обобщенного (денситометрического) числа Фруда (). C уменьшением относительного скачка плотностей при сохранении размеров движущегося тела скорость его движения, соответствующая резонансному режиму, также уменьшается пропорционально , тем не менее кинематические проявления вихре-волнового резонанса сохраняют свою интенсивность.

Если , то число Фруда (), при котором возникает резонанс, также стремится к нулю. Этот результат, хотя ему и может быть найдено разумное теоретическое объяснение, по нашему мнению, чрезвычайно значим: малые флуктуации плотности и малые скорости движения могут привести, благодаря вихре-волновому резонансу, к значительным возмущениям в стратифицированной среде (атмосфере, океане).

Аналогичные явления  могут происходить вблизи подводных хребтов или горных массивов на поверхности земли при наличии незначительных скачков плотности, вызываемых сравнительно слабыми ветрами и течениями. Так как диапазон параметров движения, порождающего вихре-волновой резонанс, очень узок, то сам резонанс возникает достаточно редко и требует создания специальных условий для своего изучения. Тем не менее возмущения, им вызванные, настолько велики, что могут явиться причиной аварий глубоководных аппаратов или самолетов, летающих в горных областях.

Вихре-волновой резонанс обнаружен экспериментально и теоретически также в ряде других случаев взаимодействия вихревых и волновых структур (например, при взаимодействии вертикально расположенного вихря с внутренними волнами в стратифицированной сплошной среде, при кавитационном обтекании несимметричных тел , когда длина присоединенной к телу паровой или газовой каверны близка к длине тела). Во всех этих случаях не только наблюдались аномально большие возмущения параметров потока (поля), но и формировались новые типы устойчивых структур, не наблюдавшиеся при обычных условиях.

Исходя из вышеизложенного, можно предположить, что появление резонансов подобного типа возможно при различных природных явлениях, в которых присутствует неоднородная сплошная среда (поле) и движущиеся в ней объекты или вихревые структуры, и даже предсказать условия их возникновения. Вихре - волновой резонанс может явиться одним из главных механизмов возникновения и стабилизации новых структур - то есть одной из причин структуро- и системоформирования, особенно для биологических объектов. Поэтому условия его возникновения и процессы, происходящие во время этого типа событий имеют особый интерес для качественной классификации событий мирового графа.

 

Не исключено, что закон сохранения энергии является результатом того, что все типы взаимодействия элементарных частиц осуществляются за счёт вихре-волнового резонанса. Это тем более вероятно, что для этих частиц энергия и частота - вещи идентичные, а условие сохранения энергии формально эквивалентно резонансному соотношению частот взаимодействующих волновых структур. 

 

Одной из возможных гипотез возникновения жизни на Земле является резонансное взаимодействие соленоидальной электро-магнитной структуры генома с грибовидной (дипольной) структурой клетки, перемещающейся в сплошной среде и в свою очередь резонансно взаимодействующей с нею.

Предсказанное теоретически и обнаруженное экспериментально явление нелинейного вихре-волнового резонанса вносит коренные изменения в существующие представления о взаимодействии структур и систем. Как показывают теоретические исследования, обнаруженное явление резонанса может проявляться  всех тех случаях, когда какая-либо жесткая или деформируемая система перемещается в неоднородной среде или взаимодействует с неоднородным полем. Такие явления могут наблюдаться в метеорологии, океанологии, астрофизике, физике плазмы,  химии , биологии , различных технологических процессах, при движении транспортных средств. Разрабатываемая теория позволяет предсказывать основное условие, при котором следует искать аналогичные явления и качественно анализировать новые резонансные структуры.

     Особого внимания заслуживает тот обнаруженный при изучении вихре - волнового резонанса теоретический результат, что при уменьшении степени неоднородности среды или поля резонансные явления, почти не затухая, перемещаются в зону очень малых относительных скоростей перемещения тела и сплошной среды (поля). Это позволяет использовать открытое явление как эффективный индикатор малых неоднородностей в среде и устройство управления, так как при резонансе значительный эффект может быть достигнут без значительных затрат энергии.

Одним из главных направлений использования открытого явления должно стать создание принципиально новых методов распознавания образов. В настоящее время ведутся интенсивные теоретические исследования, позволяющие обосновать возможность компьютерной реализации этой идеи. 

 

 

                                                   Этюд 36

 

  Классификация транспортно - информационных систем.

 

Основным свойством транспортно - информационных систем, относящихся к пятому классу предложенной нами классификации, является то, что они состоят из большого количества взаимодействующих между собой элементов (квантов), каждый из которых участвует в бифуркационных процессах. Поэтому математическое описание таких систем не может быть строго детерминированным.

В [6] показана необходимость появления в транспортно-информационных системах, участвующих в бифуркационных событиях, специального внутреннего механизма выбора. Высказана гипотеза о том, что именно развитие этого механизма, названного нами управляющей системой (контроллером), в системах волнового типа является основной причиной эволюции в природе. Построена  фундаментальная триада элементов взаимодействия [13-18], [6], включающая в себя

а) систему взаимодействующих структур;

б) поле, взаимодействующее с системой;

в) контроллер. 

В зависимости от соотношения элементов этой триады, внутри шестого класса, охватывающего практически все сложные самоорганизующиеся системы, могут быть выделены отдельные подклассы, определяемые особенностями бифуркационных процессов, происходящих с этими системами, а также структурой элементов триады.

 

а. Системы квазидетерминированного типа,

 бифуркационные процессы внутри которых оказывают незначительное влияние на их макропараметры.

Основным свойством таких систем является значительная разница масштабов между самой системой как обобщённой волновой структурой и отдельными элементами (квантами), ее составляющими. Фазовые границы этих систем, являющиеся обычно волновыми структурами, относящимися ко второму классу нашей классификации, во многом определяют их волновые свойства, для изучения которых существуют глубоко разработанные методы статистической физики и термодинамики. При этом квазидетерминированность на системном уровне допускает различные уровни детерминизма на уровне квантов. Большинство макроскопических объектов неживой природы, относятся к этому подклассу.

б. Транспортно - информационные системы, у которых реализуется иерархическая материальная и информационная связь между уровнем системы - волны и кванта - элемента.

В таких системах обычно выстраивается масштабная иерархия подсистем, каждая из которых может обладать свойствами волновых структур всех рассмотренных ранее классов. Эта масштабная иерархия имеет квазифрактальный характер. Именно в таких системах наблюдается соответствующее их квазифрактальной структуре степенное статистическое распределение масштабов элементов и подструктур [5], [33], [71-76]. Такие системы могут как сами возникнуть при изменяющихся внешних условиях поля, так и быть созданными транспортно-информационными структурами высшего уровня.

Во втором случае вне их или внутри них существует механизм, который может быть назван  "порождающим контроллером", содержащий некоторую, не обязательно полностью детерминированную программу, управляющую формированием иерархической системы.

Возможным механизмом возникновения и стабилизации таких систем может явиться механизм самоорганизованной критичности [29] или механизм масштабного резонанса, изучение которого только начинается в настоящее время.

в. Транспортно - информационные системы, способные к размножению, то есть к формированию себе подобных систем.

Способность к размножению не является прерогативой только транспортно-информационных систем. Практически в той или иной степени это свойство характерно для любых волновых систем, начиная от линейных волн. Именно благодаря этому свойству волновых, вихревых и дипольных структур, существует окружающий нас мир и мы сами. Однако, если мы переходим на уровень транспортно-информационных систем, то их размножение носит специфический характер, проявляя, особенно у живых систем, такую сложность, которую невозможно даже помыслить у структур более простых типов.

В [6] нами предложена новая математическая модель, позволяющая в рамках единой многозначной функции комплексного переменного описать как процесс роста, так и процесс размножения структур, формирующих сложную транспортно–информационную систему. Эта модель подробно изложена в четвёртой главе второй части настоящей монографии.

г. Транспортно-информационные системы, способные моделировать свою динамику и динамику окружающей среды - поля,

 и выбирать близкие к оптимальным модели бифуркационного поведения. Именно у таких систем существует и развивается, определяя их эволюцию, внутренний контроллер, названный нами гомеостатическим. К таким системам относятся все биологические объекты.

д. Транспортно-информационные системы, обладающие сознанием и творческими способностями.

Из известных нам систем такого рода пока единственными являются человек и человеческое общество.

На основе полученных теоретических результатов и широкого спектра работ других авторов, выполненных в русле синергетической парадигмы,  разработаны основы  методологии изучения транспортно-информационных систем, которые были применены к исследованию Internet[49], человека[64] и человечества [6].

В случае сложных самоорганизующихся (в частности за счет структурно-волнового резонанса) систем и структур волновой вектор-матрица, описывающий такие системы и структуры, становится достаточно сложным и состоит из большого числа иерархически вложенных друг в друга векторных и матричных элементов. При этом на каждом уровне иерархии непрерывно происходят события превращения одних структур и подсистем в другие.

 Исследование такого типа явлений требует сочетания волновых методов при анализе элементарных событий и событий, происходящих с большими массивами однородных структур и подсистем, со статистическими методами, позволяющими обнаруживать связь между различными уровнями иерархии. Если в рамках одного уровня иерархии статистические закономерности имеют, в основном, гауссову структуру, (прямое взаимодействие между однородными элементами систем часто оказывается незначительным), то статистика иерархических систем  имеет совсем иную природу – степенную, которую в последнее время интенсивно изучают в различных областях знания, связанных с функционированием сложных систем, начиная от кучи песка и землетрясений, кончая  социологическими исследованиями [5], [25], [27]

, [29], [30], [31], [32], [33]. [71-77],

.

Синергетика. Этюды 70.

Посвящено 100-летию со дня рождения выдающегося учёного, профессора

Басина Абрама Моисеевича.

Басина Г. И., Басин М. А.

НИЦ «Синергетика» Санкт-Петербургского союза учёных.

Этюд 36

О транспорте энергии и информации в волнах и структурах.

 

24 ноября 2009

 

С увеличением степени нелинейности увеличивается степень материальности, телесности, структур и систем. Всякая структура перемещается относительно среды, её порождающей. При этом , чем выше степень нелинейности структуры, тем больше степень захвата материи среды, в которой она сформирована. Возможны различные варианты. В случае линейных волн, например, электромагнитных или звуковых,  захвата материи не происходит.

 Интересный пример- гравитационные волны в жидкости или газе. С одной стороны они являются умеренно нелинейными волнами – границами раздела сред, и с этой точки зрения их скорость перемещения границы равна скорости  перемещения среды.

Однако на этой границе в свою очередь формируются линейные или  слабо нелинейные волны, перемещение которых вдоль границы  осуществляется сначала без захвата, а затем по мере увеличения степени нелинейности со всё более увеличивающимся захватом материи. При этом скорость переноса энергии отличается от скорости движения волны –скорости переноса информации. Если же граница не деформируется, что мы имеем в случае движения твёрдого тела, перемещающееся вместе с захваченной им средой и к нему применима классическая механика Ньютона. В случае деформируемых границ возникает указанная выше двойственность. В этом случае граница за счёт фрактальной деформации может стать не просто границей , а некоторой новой фрактальной структурой, переносящей как волна свою форму-информацию а также часть материи и энергии тела-волны и окружающей среды, а также самой границы, из которой она образована. В дальнейшем, будучи одновременно  и границей старой структуры, и новой структурой она может развиваться далее по следующему сценарию.

Одной из его особенностей является связанная с локальной хаотизацией диффузия, которая увеличивает размерность и энтропию вновь образовавшейся структуры, а иногда приводит к появлению новой материальной сплошной среды., и к появлению новой границы.

При этом захваченной материальной среде может быть придана новая форма движения, которая у живых организмов называется обменом веществ. Проанализируем качественно

это явление на примере поверхностных гравитационных волн. В случае линейных волн продольного переноса массы среды нет. Переносится только энергия (с групповой скоростью) и информация (форма волны), с фазовой скоростью. При этом волны, в принципе, формируют новую среду. Однако, при этом практически нет связи между структурой среды и волновыми структурами. Волны существуют как бы сами по себе.

При этом среда  и её границы определяют  длины и скорости волн. Существует практически почти полное разделение макроскопических явлений – гравитационных волновых движений – и микроскпических явлений в сплошной среде.

Увеличение нелинейности приводит к изменению характера  взаимодействия среды и волн. Начнём рассмотрение с солитона. Солитон наряду с информацией и энергией переносит с собой часть материи  среды, в которой он перемещается. Кроме того, он обладает ещё одним важным свойством. С одной стороны его длина стремится к бесконечности, а с другой стороны можно ввести некоторую конкретную приближённую длину, определяемую бугром солитона. Если рассматривать кноидальные волны, то при их анализе более явно проявляются малый и большой масштабы. Таким образом, в одной нелинейной структуре сразу проявляются два масштаба.

Значительно более явно наличие двух масштабов проявляется в ударных волнах. Нелинейность и диссипация накладывают на основные волны новый масштаб, который соизмерим с микроскопическим масштабом сплошной среды. Так как коэффициент диссипации в какой-то мере характеризует микромир, то он же характеризует и ширину ударной волны. 

Ещё более чётко эта связь прослеживается при анализе границ раздела сред, которые можно считать обобщёнными ударными волнами с переменной скоростью движения, которая в случае стационарных границ становится равной нулю. Эти границы могут состоять из одного или нескольких слоёв атомов и в них наиболее ярко проявляется связь между микроскопическими и макроскопическими свойствами вещества. Скачок физических свойств на границах имеет одновременно  и макроскопический , и макроскопический масштабы, и здесь возможно ожидать масштабных  резонансов макроскопических и микроскопических явлений. Здесь же происходят и скачки полей, приводящие к возникновению особенностей в волновых явлениях: гравитационных, электромагнитных, звуковых.

В этих же районах происходят скачки энтропии – появление информации. Здесь можно строить новые энергетические и информационные системы, здесь зарождаются кооперативные эффекты.

Обнаружение механизмов этого зарождения как в микро- так и в макрообъёмах представляет одну из узловых проблем синергетики. Если этот механизм обнаружить, то будет найден ключ к управлению процессами эффективного преобразования энергии и информации , ключ к формированию биосферы.

С этой точки зрения ещё больший интерес представляют границы раздела трёх фаз, так как это в геометрическом смысле уже линии, две размерности которых микроскопические, и лишь одна макроскопическая. Здесь возможности резонансов становятся значительно более вероятными. Свойства этих границ, особенно если они переменны, требуют особого изучения. Интересно также рассмотреть геометрию особенностей такой границы (спирализация и самопересечения) и влияние её на пересекающиеся границы раздела сред.

Ешё более интересной является гипотеза о существовании границы раздела четырёх различных сред. Эта граница является макроскопической точкой. А не в этой ли точке зародилась жизнь?  Гипотетически это могло быть следующим образом- четвёртой средой наряду с землёй, воздухом и водой,- могла быть магма, выливающаяся из вулканов.

В последние годы в районе подводных вулканов обнаружены специфические формы жизни.

Если вулкан действует в течение долгого времени на границе раздела трёх сред, то могут возникнуть четверные точки, в которых могут происходить уникальные события. Лава вулкана представляет собой особое состояние, в котором происходят фазовые переходы. Пересечение границы струи лавы с границей раздел трёх сред приводит к множественным фазовым и температурным скачкам и появлению множественных фазовых аттракторов и репеллеров различной природы. Этот режим может служить также мощным преобразователем энергии в духе Скорнякова- Зилберглейта. Все явления, которые здесь происходят, происходят на макроскопическом уровне. Однако, сама зона четверного пересечения уже   является зоной микроскопического – нанауровня. Возможно, она является источником появления специфических структур, являющихся источниками жизни.

Всякая неравновесная открытая структура существует и развивается за счёт поступления материи, энергии и информации, которые перерабатываются внутри неё, трансформируются, становятся её элементами. Одновременно она выбрасывает из себя не нужную ей материю, энергию, информацию, или передаёт их другим структурам в качестве обмена. Чем сложнее структура, чем из большего количества различных элементов она состоит, и чем больше она организована, тем больший объём материи, энергии и информации ей требуется. Известно, что в замкнутых однородных структурах действует второй закон термодинамики, утверждающий, что степень неорганизованности  (энтропия) в таких системах только растёт. Иное дело- открытые системы. За счёт поступления энергии, носителями которой являются поля или вещество, такая система может постоянно уменьшать свою энтропию и развиваться, то есть вырабатывать новую информацию, рост которой приводит появлению связей и самоорганизации.

Материя, энергия и информация приходят в систему извне и должны каким-то образом транспортироваться или постоянно присутствовать в окружении системы. Внешняя транспортировка может быть двоякой

А) пассивной

Б) активной

Пассивная транспортировка заключается в том, что система находится в окружении других систем, функционирование которых приносит к её границам частицы материи, энергию, информационные поля, которые могут восприниматься, пропускаться или отражаться системой.

Любая сложная система является своего рода волной –движущейся  в пространстве и встречающейся с частицами материи, энергией  и информацией, производимой другими структурами. При этом внешние воздействия можно условно разделить на «полезные» и «вредные».

«Полезные» вещество, энергия, информация – это та материя, наличие которой позволяет структуре сохранить стабильность, сохранить или уменьшить энтропию, а, возможно, даже повысить  количество постоянно циркулирующей в системе информации и усложнить её структуру.

«Вредные» вещество, энергия, информация –это те элементы окружающего мира, которые потенциально могут либо разрушить структуру, либо ослабить уровень её функционирования, тем самым увеличить  энтропию структуры.

По-видимому, существует какой-то закон существования сложных неравновесных структур, который на определённом этапе их существования вступает в противоречие со вторым законом термодинамики и «заставляет» структуры стабилизироваться за счёт сохранения гомеостаза и увеличения внутренней массы, энергии и информации. Этот закон должен быть диалектическим дополнением второго закона термодинамики

Наряду с пассивной транспортировкой вещества. энергии и информации, возможна также активная транспортировка. Система, повинуясь закону «развития», отталкивает от себя «вредные» и притягивает к себе «полезные» элементы окружающей среды. Для этого она должна быть достаточно хорошо структурирована, чтобы заранее различать полезные или вредные элементы, или обладать «памятью», то есть органами сохранения информации.

 

                                                                      Этюд 37

 

 Квазидетерминированные процессы..

 Взаимодействие структур. Целостность процесса

 

Цепочка детерминированных и (или) бифуркационных событий, в результате которой происходит взаимодействие входящих в систему структур и появляются новые структуры или исчезают старые, была названа процессом.

С другой, внешней, стороны в графе структур и событий могут быть выделены определенные области (ветви), начинающиеся с какого-либо события и кончающиеся каким-либо другим событием, которые обладают некоторой независимостью от остальных областей графа . В связи с этим

под процессом можно понимать также некоторую, относительно независимую ветвь графа структур и событий

Сечения процесса по некоторому моменту времени могут быть представлены как вектор - матрицы данного процесса (как некоторой части графа структур и событий).

Если рассматривать процесс, в котором участвует та или иная система, не снаружи, с позиции всей системы, а изнутри, с позиций отдельной структуры, входящей в исследуемую систему, то для неё этот процесс можно представить некоторой индивидуальной траекторией внутри графа структур и событий, или траекторией внутри процесса (некоторым аналогом мировой линии Ньютоновой механики). При прохождении этой траектории, сохраняя в какой-то степени свою индивидуальность, структура вступает во взаимодействие с другими структурами системы, в течение некоторого времени формирует с ними комплексные структуры, затем эти структуры либо усложняются, включая в себя все новые элементы, либо распадаются с возвращением структур в прежнее состояние.

Если рассматривается процесс, ограниченный во времени, то можно ввести в рассмотрение некоторый отрезок времени, начало которого может считаться началом процесса, а конец - его окончанием. Введение такого отрезка времени и самого факта взаимодействия структур позволяет сформировать в системе некоторую метрику, характеризующую в первом приближении взаимодействие структур в системе, а следовательно, дающую количественную оценку ее целостности.

Предположим, что построена траектория некоторой структуры . При этом можно определить время , в течение которого структура участвовала в построении комплексных структур совместно со структурой . Это время составляет некоторую часть от времени прохождения процесса . Можно ввести понятие относительного времени взаимодействия структур  и  в процессе . Во многих случаях эта величина слабо зависит от величины , то есть от принятой нами условной длины процесса. Тогда ее можно считать устойчивой характеристикой взаимодействующих между собой структур  и , или вкладом структур  и  в целостность процесса.

Такую процедуру можно осуществить для всех пар взаимодействующих структур и снабдить каждую из пар своей величиной относительного времени взаимодействия. Если величина   стремится к единице, то структуры  и  совместно включены в новые структуры в течение всего исследуемого процесса и их совместный вклад в целостность процесса максимальный. Если , то структуры между собой не взаимодействуют.

Рассмотренный подход позволяет ввести внутри системы некоторую метрику, определяющую средние "расстояния" между отдельными структурами. Эти "расстояния" - могут быть определены как величины, обратно пропорциональные величинам .  

                                                  (7.1)

Если принять , то есть "расстояние" структуры от самой себя равно нулю, то минимальное "расстояние" между взаимодействующими структурами соответствует случаю, когда , то есть когда структуры, сохраняя свою индивидуальность, взаимодействуют в течение вcего времени .

Чем меньше величина  , тем больше введенное нами расстояние между взаимодействующими структурами. Если , то .

Если начать построение метрики с какой-либо одной структуры , то можно определить все структуры, которые взаимодействуют с ней в рамках данного процесса. Изображение их на шкале расстояний позволит включить сюда все структуры, расстояние которых от данной меньше бесконечности. Если для каждой из включенных в эту шкалу структур вновь построить шкалу расстояний до нее других структур, и эту цепочку действий продолжать до тех пор, пока новые структуры не перестанут появляться, мы получим систему, являющуюся подсистемой данной системы, и включающую в себя часть её элементов. Со структурами, не вошедшими в построенный нами подпроцесс, можно осуществить ту же операцию и построить другой подпроцесс изучаемого процесса.

Тем самым, введение предложенной метрики позволяет разбить изучаемый процесс (а может быть и весь граф структур и событий)  на совокупность независимых друг от друга и не связанных между собой в течение исследуемого промежутка времени целостных процессов, внутренние метрики которых не связаны между собой.

Однако, предложенный алгоритм содержит принципиальный недостаток, который может быть ликвидирован введением некоторого нового параметра.

Ни одна из систем природы, ни один из исследуемых процессов не может быть полностью выделен из окружающего мира. Таким образом, предложенная выше идеализированная схема не может быть реализована в своем чистом виде. Расстояния между отдельными структурами никогда не могут быть приняты равными бесконечности. Все структуры, существующие в природе находятся на некотором конечном "расстоянии" друг от друга, и отделение независимого процесса от всего процесса развития Вселенной невозможно.

Однако это можно сделать приближенно.  Для этого необходимо ввести новое понятие - максимального радиуса взаимодействия структур в рамках данного процесса . Введение этой величины эквивалентно постулированию минимально допустимой величины относительного времени взаимодействия . Назначение этой величины является субъективным решением наблюдателя - исследователя в каждом конкретном случае. Чтобы исключить субъективность, можно ввести шкалу последовательно увеличивающихся (либо уменьшающихся) величин максимально допустимых расстояний между взаимодействующими структурами Введя соответствующее максимально допустимое расстояние между взаимодействующими структурами, мы можем повторить изложенную ранее процедуру. В этом случае в рассматриваемый подпроцесс попадут лишь те структуры, "расстояние" которых до хотя бы одной из структур, входящих в выделяемую подсистему, окажется меньше . Все остальные структуры попадут в другие подсистемы исследуемой системы или будут включены в поле данного подпроцесса.

Подобное разделение процесса на подпроцессы является приближенным, и степень приближения определяется величиной .

Метрика  процесса  может быть введена и другим способом, например может быть использована модификация естественной метрики пространства.

Пусть имеем два отделенных друг от друга с радиусом  процесса. Для каждого из них может быть вычислена своя максимальная величина

                                                                целостности,

 которая определяется как сумма относительных времен взаимодействия всех входящих в систему пар структур.

Их число равняется ; где - число элементарных структур,  входящих в систему.

Целостность процесса может быть определена в соответствии с формулой

 ,                                                     (7.2)

где суммирование ведётся по всем парам взаимодействующих между собой структур.

Эта же величина может быть выражена через  расстояния между элементарными структурами (7.1), входящими в систему

                                                      (7.3)

Максимальное значение целостности системы и соответствующего ей процесса достигается тогда, когда все входящие в неё элементарные структуры во все время процесса формируют единую структуру. В этом случае все значения  оказываются равными 1, и величина целостности :

.                                           (7.4)

Возможным также оказывается и введение относительной целостности процесса как отношения целостности процесса к максимально возможной  целостности того же процесса.

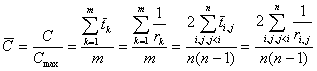.                (7.5)

Одновременно с целостностью всего процесса целесообразно рассмотреть  еще одну, близкую к ней величину, однако относящуюся к отдельной элементарной структуре.

Эта величина может быть названа связанностью -той элементарной структуры .

,                                                    (7.6)

Она характеризует суммарное относительное время взаимодействия данной структуры с остальными структурами системы. Максимальная величина связанности элементарной структуры, входящей в систему из  элементарных структур, равна . Тогда относительная связанность структуры в рамках выделенного процесса определяется в соответствии с формулой

.                                             (7.7).

Между связанностями структур, входящих в процесс, и целостностью процесса существует простая связь, определяемая следующей формулой.

.                                          (7.8)

Аналогичная связь может быть установлена и между относительными величинами.

.                           (7.9)

 

Относительная целостность процесса определяется как среднее арифметическое от относительных связанностей структур, входящих в данный процесс.

 

Однако одного понятия максимального радиуса недостаточно для отделения одного процесса от другого. Это связано, например, с тем, что могут существовать элементарные структуры, расположенные на расстоянии, большем, чем от почти всех структур данного процесса, но на расстоянии, меньшем, чем  ,  от одной или нескольких структур, однако имеющие значение  - меньшее, чем аналогичное значение у структур, которые мы не включили в систему, участвующую в процессе по первому критерию. Тем самым, среди периферийных структур данного процесса мы выкидываем одни из них, вносящие больший вклад в целостность системы, по оставляем другие, вносящие меньший вклад. 

Для более рационального разделения процессов следует в этом случае принять следующую процедуру. Первоначально исключить из процесса все структуры по критерию максимального радиуса. Затем для исключенных структур вычислить величины связанностей каждой из них. Определить максимальную величину связанности для выброшенных из процесса структур. Затем вычислить связанность всех оставшихся структур, и исключить из процесса все структуры, имеющие связанности, меньшие этой максимальной величины. В этом случае можно с достаточной степенью достоверности исключить из системы структуры по двум перевязанным между собой и не противоречащим друг другу критериям.

Однако, более подробный анализ показывает, что и этого оказывается недостаточно, так как не учитывается еще один - локальный критерий разделения.

Прежде, чем ввести такой критерий, необходимо рассмотреть понятие связи между двумя не взаимодействующими прямо между собою структурами.

Для введения такого понятия достаточно рассмотреть систему, состоящую из трех элементарных структур , взаимодействующих между собой с образованием комбинированных структур. Если предположить, что структуры  между собой вообще не взаимодействуют, а структура  взаимодействет как со структурой , так и со структурой , то можно, задаваясь величинами , определить связанность каждой из структур, а также целостность всего процесса.  Если мы исключим структуру  из анализа системы, то процесс в рамках нашего анализа автоматически разобьется на два независимых процесса, происходящих со структурами . Структура , оказавшись вне их, будет периодически включаться то в процесс , то в процесс , осуществляя опосредованную связь между ними. При этом интенсивность связи, в отличие от случая непосредственного взаимодействия между структурами, несимметрична относительно структур , например, . Одним из возможных критериев интенсивности связи может служить минимальное из двух значений , которое может быть обозначено . Структуру  можно назвать агентом связи.

Таким образом, наряду с непосредственным взаимодействием элементарных структур между собой, целесообразно рассматривать еще один механизм - механизм взаимодействия через агентов связи, который может оказаться не менее важным, чем первый, особенно в случае анализа процессов, включающих в себя бифуркационные события.

При этом структура  может быть включена в процесс, соответствующий той из оставшихся структур, связанность её с которой больше. А связь этой структуры с другой будет характеризовать взаимодействие разделенных процессов. 

 Пусть мы имеем некоторый процесс, происходящий с системой, состоящей из достаточно большого числа взаимодействующих между собой структур. В соответствии с разработанной выше процедурой попытаемся построить подпроцесс, включая в него только структуры, удовлетворяющие двум указанным выше критериям. Получим некоторую совокупность структур, образующих подсистему, входящую в первоначальную систему, которая может быть названа ее полем. Пусть подсистема, участвующая в этом подпроцессе может быть разделена еще раз на две группы структур, которые в рамках введенных нами ограничений не взаимодействуют непосредственно между собой и казалось бы в этом случае выделенный нами подпроцесс может быть разделен на две части. Однако мы не можем этого сделать, так как среди включенных в него структур существует одна или несколько, которые укладываются во все вышеуказанные ограничения и одновременно находятся на достаточно близком расстоянии от обеих указанных групп структур. Эти структуры могут быть названы структурами-связями или структурами - мостами.

Удаление таких структур из рассматриваемой подсистемы приводит автоматически к разделению её и процесса, в котором она участвует, на части. После такого разделения указанные структуры - связи или структуры - мосты, которые могут быть включены в процесс - поле, становятся основными элементами взаимодействия разделенных процессов.

Мы считаем, что выделение в процессах и подпроцессах одной или нескольких структур-мостов - и удаление их из подсистемы в поле должно стать частью алгоритма разделения сложной системы на подсистемы, сложного процесса на подпроцессы.

При этом должно быть заранее задано число структур, которые должны быть удалены одновременно. Самым простым способом является перебор всех сочетаний из структур, уже вошедших в подсистему по числу структур, которые должны быть удалены из подсистемы начиная от единицы и до заданного числа. Для каждого такого сочетания должна быть осуществлена проверка на разделимость. И если она выполняется, то соответствующие структуры удаляются из системы, а сама она разделяется при этом на части. Выброшенная при такой процедуре структура может быть либо отнесена к полю, либо включена в ту часть разделенного процесса, с которой она больше связана, суммарная связанность со структурами которой оказывается максимальной.

Среди структур-связей может оказаться особый класс, обладающий следующим свойством. Такая структура связана с несколькими структурами одного подпроцесса и может быть после разделения включена в этот процесс, и лишь с одной структурой другого подпроцесса, которая обладает аналогичными свойствами относительно своего подпроцесса. В этом случае в каждом процессе существует по структуре, каждая из которых связана лишь с одной определенной структурой другого процесса.  Такие мостовые структуры могут считаться граничными структурами процессов. По ним также можно отделять процессы друг от друга. Если в разделяемом процессе существует любое количество граничных структур, при процедуре разделения они все должны быть выброшены, чтобы затем присоединить соответствующие структуры  каждую к своему процессу.

Пусть имеем два процесса, (1 и 2) отделенные друг от друга с некоторым радиусом . Тогда в рассматриваемом случае под мерой взаимодействия процессов можно понимать некоторую величину, которая может быть определена следующим образом. Внутри каждого из процессов существуют структуры, взаимодействующие, хотя и слабо, со структурами другого процесса. Величина этого взаимодействия определяется для каждой структуры одного из процессов, как и ранее, суммарным относительным временем взаимодействия со всеми структурами другого процесса. Эта величина может считаться интенсивностью взаимодействия данной структуры, принадлежащей к процессу 1, со всеми структурами, принадлежащими к процессу 2, или связанностью структуры процесса 1 с процессом 2.

                                                 (7.10)

В последней формуле , - номер структуры, принадлежащей к первому процессу. - номер структуры, принадлежащей ко второму процессу. - число структур, входящих во второй процесс. 

Полная величина взаимодействия между процессами (или системами, участвующими в процессе) определяется по формуле:

.                   (7.11).

Пусть имеется некоторый процесс, для которого выполнена описанная выше процедура разделения процесса на составляющие подпроцессы. Если принять максимальный радиус взаимодействия равным бесконечности, то процесс оказывается неразделимым. Уменьшая максимальный радиус, мы увеличиваем число подпроцессов, на которое может быть разделён наш процесс. Аналогично, увеличивая при постоянном значении максимального радиуса величину допустимого числа мостовых структур, мы также можем увеличить число подпроцессов, на которое может быть разбит наш процесс.

При этом для каждого значения указанных параметров получается свое значение величины взаимодействия выделенных подпроцессов.

В предельном случае, когда принятое нами максимальное расстояние между структурами оказывается меньше 1, исследуемый процесс разделяется на  подпроцессов, каждый из которых описывает динамику отдельной элементарной структуры. Зависимость числа выделяемых подпроцессов, а также степени их взаимодействия от изменения двух основных задаваемых исследователем параметров позволяет достаточно подробно проанализировать внутреннюю топологию исследуемого процесса - составить его "образ". При этом наиболее характерными становятся те значения управляющих (управляемых нами) параметров, при которых происходит качественное изменение картины, а именно существенно изменяется число рассматриваемых подпроцессов. Тем самым, мы получаем «паттерн» исследуемого процесса и каждого из его подпроцессов, который в течение некоторого времени может считаться постоянным. Взаимодействие подпроцессов в рамках этого паттерна может быть названо фоновым взаимодействием.

 Предположим, что в рамках данной большой системы, состоящей из взаимодействующих подсистем, паттерн взаимодействующих подсистем меняется медленно по сравнению с частотой, с которой взаимодействуют между собой отдельные структуры. В этом случае можно ввести два масштаба времени - масштаб времени, соответствующий взаимодействию структур внутри подсистем, и масштаб времени, соответствующий характерным изменениям паттернов фонового взаимодействия. Характерное время , введенное  ранее, занимает промежуточное положение между этими двумя масштабами. При исследовании взаимодействия процессов в макро-временном масштабе можно  ввести следующую процедуру. Рассмотреть макроскопический масштаб времени, внешний по отношению к масштабу , и в рамках этого масштаба ввести в рассмотрение понятие времени начала отсчета - текущее время. Для каждого значения текущего времени, рассматривать малый по сравнению с внешним масштабом промежуток времени , в рамках изменения которого паттерн процесса, который на этом промежутке можно считать стационарным, слабо меняется. Этот паттерн можно считать присущим макроскопическому моменту времени .

Аналогичную процедуру можно осуществлять для некоторой последовательности значений . Если изменения паттернов окажутся гладкими, то можно ввести асимптотическое представление о гладкой зависимости паттерна взаимодействующих процессов от времени, о скоростях изменения паттерна от времени - то есть построить соответствующие дифференциальные уравнения.

Рассмотрим три характерных случая  макровременного взаимодействия.

 Непосредственное взаимодействие двух выделенных процессов. Пусть при помощи описанной выше процедуры нам удалось все основные структуры, включённые в данную систему, отнести к двум различным подсистемам, то есть разделить некоторый процесс на два подпроцесса.

 Пусть на некотором промежутке времени  оба подпроцесса можно считать установившимися. Тогда в каждый макроскопический момент времени  возможно построить паттерн обоих взаимодействующих процессов и вычислить их фоновое взаимодействие.

Выберем некоторые значения управляющих параметров и допустимого числа удаляемых мостовых частиц. Затем выполним с этими значениями управляющих параметров процедуры разделения процессов и вычисления их фонового взаимодействия для различных моментов времени. Тем самым получим сечение по управляющим параметрам последовательности паттернов взаимодействующих процессов во времени. При этом на каждом шаге по времени вследствие изменения паттерна  будет изменяться не только величина фонового взаимодействия процессов, но, что намного более важно и существенно, число структур, которые входят в каждый из процессов. Мостовые  и граничные структуры будут менять свои связи в обоих процессах и переходить из одной подсистемы в другую, из одного подпроцесса в другой. При этом они могут уходить в центральную часть процесса. Может происходить и обратное явление ухода структур на периферию процесса . Тем самым, хотя разделение на два процесса будет оставаться, внутренняя структура, в том числе и целостность каждого из них изменяются значительно. При этом наиболее важным является тот факт, что многие элементарные структуры, входившие сначала в один процесс через некоторое время оказываются в другом.

Пусть в момент времени  в первой из взаимодействующих систем находится  основных структур, а во второй  . Рассмотрим некоторый новый момент времени  , отличающийся от  на величину . В этот момент состав систем, участвующих в первом и втором процессах, изменится. В первой из взаимодействующих систем окажется  элементарных связанных между собою структур, а во второй системе -.

Целостность подпроцессов - обобщённых волн - формируется на микровременном уровне. Однако с изменением макровремени, два взаимодействующих целостных процесса претерпевают существенные изменения. Структуры могут переходить из одной подсистемы в другую, из одного процесса в другой.

За промежуток времени   из первой системы во вторую перейдет  элементарных структур, а из второй системы в первую -  структур. Тогда, если элементарные структуры никуда не исчезают, то есть выполняется закон сохранения элементарных структур, то мы можем получить следующие соотношения.

-                                                  (7.12)

                                                          

 

 Введем величину

.                             (7.13)

Отношение величины   к промежутку времени , определяет некоторую среднюю скорость изменения взаимодействующих систем.

                                                   (7.14)

Если участвующие во взаимодействии элементарные структуры имеют приблизительно одинаковую меру, то, умножая правую и левую части последнего равенства на эту величину, которую обозначим , получим следующее равенство

 .                           (7.15)

Осредненная разность потоков меры между процессами определяется как отношение приращения меры в процессе, увеличившем свой "объём", к исследованному промежутку времени.

Выберем конечную последовательность  уменьшающихся отрезков времени таким образом, чтобы  оставалось значительно больше . И построим последовательность осредненных разностей потоков. Если график изменения  асимптотически выходит на величину,

                                       (7.16)

то эта величина может быть названа величиной неравновесности, или асимптотической производной от изменения меры процессов по времени.

При этом для каждого из взаимодействующих процессов эта величина может быть взята со своим знаком. Для процесса, увеличивающего свою меру, - со знаком плюс, для процесса, уменьшающего свою меру - со знаком - минус.

     Если первый процесс увеличивает  меру, то

                                                            

Во многих случаях можно забыть о последовательности вывода  этих асимптотических соотношений и опустить индекс , обращаясь с соотношениями, входящими в предыдущие формулы как с обычными производными.

 

                        (7.17)

 

Последние формулы могут оказаться справедливыми и в случае, если элементарные структуры специально не могут быть выделены, а обмен "мерой" происходит за счет более сложных структур, однако, измеряемых одной аддитивной мерой, хотя значения её могут быть различными для каждой из участвующих в процессе структур. При этом величина  вычисляется как модуль разности суммы мер структур вышедших из данного процесса и суммы мер структур, в него вошедших.

Анализируя динамику изменения меры каждого из взаимодействующих процессов, мы можем перейти к рассмотрению либо системы двух связанных между собой дифференциальных уравнений , либо к системе итерационных соотношений - характеризующих изменения основной аддитивной меры взаимодействующих процессов.

Макро-временное взаимодействие может быть описано еще одним параметром, характеризующим интенсивность обмена элементарными структурами между взаимодействующими процессами. Эта величина определяется как полусумма числа структур вошедших за промежуток времени , например, в первый процесс, и числа структур, вышедших из него. 

                                       (7.18)

Разделив величину  на и проведя асимптотическую процедуру, аналогичную той, которая выполнялась нами в предыдущем случае, получим асимптотическую скорость обмена структурами

 

                                       (7.19)

По аналогии с предыдущим можно ввести также величину скорости обмена  мерой

.                                   (7.20)

Интересен случай, когда в процесс входят все новые и новые структуры, а уходят из него уже побывавшие в нём.  В этом случае можно выбрать такой промежуток времени , при котором в  конце промежутка в одной из систем не останется ни одной из структур, бывших в ней в начале промежутка. Тем самым, процесс остается все тем же процессом , но в нем уже нет ни одной старой структуры. При этом может оказаться так, что картина связей - уже между новыми структурами, занявшими место прежних будет сохраняться той же. В этом случае процесс становится похожим на классическую волну, сохраняющую свой паттерн при полной замене структур, в нее входящих. Для такого процесса может быть введена и новая величина , период циркуляции структур внутри процесса, приближенно определяемая как отношение

                                           (7.21)

Здесь  - величина аддитивной меры, соответствующей данному процессу.

Период циркуляции структур характеризует свой для каждого из взаимодействующих процессов период процесса как некоей циклической волны, перемещающейся по полю структур, входящих в оба взаимодействующих процесса. Фактически этот период характеризует то, что мы называем обменом веществ.

Однако, этот случай является лишь предельным возможным случаем волнового взаимодействия процессов.

Другим предельным случаем является вариант, когда во взаимодействии участвуют только те мостовые структуры, которые были названы нами пограничными.

Предположим, что при взаимодействии систем, входящих в процессы, не происходит переход  структур из одного процесса в другой. Считаем, что все мостовые структуры, осуществляющие основное взаимодействие - являются граничными; каждая из них связана лишь с одной граничной структурой другого процесса. Сцепленные между собою граничные структуры формируют некоторые новые структуры. Совокупность таких структур может быть названа общей границей обоих взаимодействующих процессов. Динамика взаимодействия процессов в этом случае характеризуется динамикой их общей границы.

Сама граница становится новой системой, обладающей своей динамикой, а оба взаимодействующих процесса становятся полем существования такой системы. Это один из механизмов формирования и существования умеренно-нелинейных волновых структур (второй класс нашей классификации). Возникают три специфически взаимодействующих процесса. Два первых взаимодействуют между собой через третий процесс - процесс границу, процесс посредник, делегируя в него свои граничные структуры.

Динамика такого взаимодействия может быть классифицирована следующим образом.

1.    Граница остаётся неизменной. Одни и те же структуры одного процесса взаимодействуют с одними и теми же структурами другого. Процесс взаимодействия может считаться стационарным.

2.    Взаимодействие качения. Структуры, образующие границу  не меняют своих партнеров. Они могут либо разрывать свои связи и уходить внутрь своих процессов, либо образовывать новые, выходя на границу.

3.    Взаимодействие скольжения. Структуры, входящие в границу, меняют своих партнеров, однако постоянно остаются на границе.

4.    Смешанное поведение. 

В результате взаимодействия качения и смешанного поведения граница может либо захватить один из взаимодействующих процессов, либо исчезнуть. При этом процессы перестанут взаимодействовать между собой.

 

Между двумя рассмотренными выше механизмами макровременного взаимодействия процессов лежит область механизмов взаимодействия, занимающая все возможные комбинации с существованием границ и обмена структурами между ними.

При этом  могут появляться переходные слои, элементы которых, не являясь границами в указанном выше смысле, активно участвуют во взаимодействии, тогда как основные части - ядра - систем участвующих в процессах,  в их взаимодействии участвуют лишь через внутреннее взаимодействие с переходными слоями. Эти переходные слои чаще всего могут быть отнесены ко второму классу нашей классификации - умеренно-нелинейным волнам. [12]

Одним из главных результатов взаимодействия может оказаться  слияние процессов, Противоположным событием является, например, расщепление одного из взаимодействующих процессов, или обоих на несколько более мелких подпроцессов, которые либо будут существовать раздельно, взаимодействуя между собой, либо войдут в систему последовательных расщеплений, аналогичных сценарию возникновения хаоса в результате цепочки бифуркаций.

Физическим примером такого взаимодействия может являться формирование брызг.

 Социологическим - формирование и распадение Империй.

Второй вариант взаимодействия процессов - взаимодействие некоторой системы и её поля.

Этот вариант в некотором смысле является частным случаем предыдущего. Однако второй из взаимодействующих процессов оказывается как бы вне первого. Он содержит значительно больше элементарных структур. Дополнительной существенной особенностью взаимодействия системы и поля обычно является тот факт, что элементарные структуры, формирующие поле,  часто имеют значительно меньшие значения меры, чем структуры, формирующие систему, что придает взаимодействию специфические особенности.

Во многих случаях в поле может быть введена непрерывная континуальная геометрия. Введение такой геометрии требует достаточно тонких рассуждений, позволяющих перейти от дискретной метрики взаимодействующих структур, введенной нами ранее, к непрерывной римановой метрике в мерном непрерывном многообразии, что позволяет использовать для исследования особенностей взаимодействия структуры и ее поля развитую в настоящее время теорию гладких расслоений [24].

 

Третий вариант , когда два процесса взаимодействуют при наличии поля, вносит нечто принципиально новое в вышеприведенное рассмотрение.

Кроме непосредственного взаимодействия процессов, описанного в случае первого варианта, возникает еще один механизм взаимодействия - взаимодействие через поле.

 Каждый из взаимодействующих процессов обменивается с полем элементарными структурами. Тем самым, через изменение поля происходит дополнительное к прямому  полевое взаимодействие процессов. Те структуры, которыми поле обменивается с одним из процессов влияют на характеристики поля, тем самым влияют на характер обмена структурами между полем и вторым процессом. Это взаимное влияние оказывается интегральным - волновым - происходящим одновременно с существенным изменением поля, через которое и происходит само взаимодействие процессов.

Однако, в некоторых случаях взаимодействие процессов через поле оказывается и более непосредственным. Структуры, вышедшие в поле из одного процесса, могут достаточно быстро попасть из поля в другой процесс. Поток таких  структур - агентов формирует еще один механизм взаимодействия процессов, который может быть назван взаимодействием посредством связей между двумя процессами, осуществляемыми через поле.

Интенсивность связей определяется, как и ранее, числом структур-агентов (или их суммарной мерой), вышедших из одного процесса и вошедших в другой. Все рассуждения, которые были проведены ранее, могут быть повторены для связей. Однако, в данном случае элементарная структура, выйдя из одного процесса, некоторое время находится в поле, и лишь затем оказывается в области действия другого процесса. Появляется новый параметр - время задержки связи. Поле формирует внешнее пространство, в котором структуры-связи функционируют, пока они не попали из одного процесса в другой.

 

Этюд 38

Бифуркационные процессы.

 

Все выполненные выше модельные построения, строго говоря, справедливы только для детерминированных структур и систем, включаемых в детерминированные процессы. Существование бифуркационной проекции графа структур и событий существенно усложняет постановку и решение проблемы взаимодействия процессов.

Под бифуркационным процессом будем понимать такой процесс, который включает в себя хотя бы одно бифуркационное событие.

При исследовании бифуркационных процессов необходимо наряду с непосредственным взаимодействием структур и подсистем, формирующих данный процесс, исследовать их виртуальное взаимодействие.

Непосредственное предсказание всех возможных исходов взаимодействия бифуркационных процессов было бы в принципе невозможно, если бы в природе не существовало идентичных или почти идентичных структур, систем, процессов (квантов), которые уже участвовали в бифуркационных событиях. Все такие идентичные структуры, системы, процессы могут быть объединены в классы, названные нами обобщенными волнами.

Большинство реальных транспортно- информационных систем  может быть включено в иерархию волн – квантов. При этом, с одной стороны, изучаемая система является квантом для некоторой волны, которая представляет собой совокупность систем (квантов), аналогичных данной системе, а с другой - она является волной для своих первичных элементов. Иерархия волн - квантов обычно имеет масштабно-квазифрактальный характер и практически всегда может быть линейно продолжена как в сторону увеличения, так и в сторону уменьшения масштабов. При этом каждый уровень иерархии может быть рассмотрен как волна и как квант, в зависимости от масштаба рассмотрения.

Если экспериментально исследовать некоторый единичный бифуркационный процесс, то мы имеем дело лишь с одним из многочисленных виртуальных путей, разрешенных для процессов, аналогичных данному, выбранным им в данной реализации. Такой процесс становится для нас квази-детерминированным и его модельный количественный анализ может быть проведен по изложенному выше алгоритму.

Однако, полученный результат сам по себе не имеет предсказательной силы, так как в другом аналогичном случае процесс может пойти по любому другому из разрешенных ему путей. Мы пока ничего не знаем о поведении процесса в этих нереализованных вариантах. Экспериментально эти пути и даже вероятности следования по ним можно определить только в результате анализа взаимодействия совокупности идентичных или почти идентичных бифуркационных процессов.

Cистеме, участвующей в бифуркационных событиях, может быть при ее исследовании сопоставлена целостная триада [13-18], [6],

 

                                                 Поле

                                        (Ближнее и Дальнее)

                                         /                     \

            Структура (система) ------------- (Контроллер)

(Материальная часть системы)      (Управляющая система)

 

Рассмотрим эту триаду более подробно.

Структура (система)– это материальная часть объекта, которая, взаимодействуя с полем, (в основном, ближним) участвует в бифуркационных событиях – то, что Тейяр де Шарден называл внешней - видимой - частью объекта [10].

 Поле – это внешняя по отношению к системе совокупность объектов, породившая систему или родившаяся вместе с ней, интенсивно взаимодействующая с системой, при этом некоторые события, происходящиe при таком взаимодействии, являются бифуркационными, то есть события  имеют некоторый набор возможных исходов. Поле может быть условно разделено на ближнее, наиболее интенсивно взаимодействующее со структурой, и дальнее, влиянием которого при данном уровне рассмотрения можно пренебречь. Несмотря на условность такого разделения, практически оно очень важно.

Контроллер (управляющий механизм) – внутренний механизм системы, позволяющий выбрать из числа возможных исходов того или иного события, тот, который приведет к наиболее устойчивому состоянию системы. Его главная задача – выбор и обеспечение реализации такого исхода бифуркационного события, который обеспечит наибольшую устойчивость как структуры, так и ее поля, а также самого управляющего механизма.

Количество и вероятность исходов бифуркационных событий, происходящих при волновом взаимодействии структуры и поля, определяются как свойствами самой структуры, так и поля, в котором она существует. Поэтому контроллер, возникающий в структуре, непосредственно связан как с характеристиками поля, так и с внутренней структурой системы. 

Его «цель» - при увеличении числа возможных исходов обеспечить такое уменьшение энтропии будущего бифуркационных событий, которое одновременно сохранило бы  максимальное число инвариантов структуры, поля и самого контроллера и обеспечило бы резонансное согласование между ними. Только структуры с таким контроллером  могут «выживать» в условиях сложных внешних полей.

Появление контроллера включает в действие механизм эволюции, причем эволюционируют в непосредственной связи между собой все три элемента триады. Возникает тройное резонансное взаимодействие, приводящее к последовательному увеличению сложности и динамической устойчивости (увеличению числа возможных исходов бифуркацонных событий и информации, хранимой и перерабатываемой контроллером). Более подробный анализ каждого из элементов, включённых в триаду, выполнен в [6].

 Рассмотрим взаимодействие этих элементов между собой

 

Взаимодействие контроллера и структуры.

 

Контроллер – это механизм управления бифуркационными процессами, включающими рост и развитие структуры (системы). Контроллеры могут быть двух типов.

1.    Контроллер, порождающий структуру.

2.    Контроллер, обеспечивающий устойчивое существование структуры, выбор её поведения при взаимодействии с полем, способный до начала событий изменять вероятности реализации возможных результатов, а также осуществляющий в момент события выбор того или иного конкретного результата - гомеостатический контроллер.

 

Гомеостатический контроллер может выполнять следующие основные функции.

1. Воспринимать практически непрерывный поток информации об окружающей среде – поле - и запоминать этот поток информации. Носителями этого потока информации, практически не опасными для гомеостаза системы могут являться потоки структур, несущие с собой малую меру, но значительный объем информации о происходящих в поле бифуркационных процессах.

2. Формировать на основе анализа полученного и запомненного потока информации образы структур и процессов, взаимодействие с которыми в будущем может принести данной системе существенные структурные изменения. 

3. Сопоставлять сформированные образы структур и процессов с текущим потоком информации.

4. Уточнять за счет этого выделенные ранее образы и процессы.

5. Классифицировать постоянно выделяемые и уточняемые образы и процессы.

6. Вводить в анализ обобщенные абстрактные образы и процессы (модели), обладающие характерными для целого класса образов и процессов инвариантами.

7. Создавать абстрактные образы, определяющие количественные соотношения между квантами и волнами. (Рождение в контроллере математических представлений об окружающем мире).

8. Отождествлять выработанные в контроллере модели с динамическими картинами, получаемыми контроллером в настоящее время.

9. На основе приобретенного знания предсказывать возможные альтернативные пути развития происходящих в настоящее время процессов (достройка на основе приобретенного знания вероятных ветвей будущих событий графа структур и событий).  

10. Оценка безопасности каждого из возможных путей развития событий, в котором структура будет сохранена в будущем.

11. Оценка на основе внутреннего статистического анализа данного класса процессов вероятности реализации каждого из альтернатвных путей развития как благоприятных, так и неблагоприятных событий, которые могут произойти в будущем.

12. Выбор наиболее благопрятного пучка исходов событий. Попытки увеличить вероятность этих исходов за счёт извлечения из числа практически невероятных некоторых новых состояний, управляемых контроллером. Именно эта функция контроллера наиболее сильно развита у человека и человеческого общества.

13. Увеличение выживаемости структуры (кванта) за счет размножения

14. Разработка кодов, определяющих реализацию целей, поставленных в результате моделирования. Выбор одного пути или пучка возможных путей в графе структур и событий, обеспечивающего, по данным контроллера, оптимальные условия выживания управляемой структуры и самого контроллера.

15. Создание и использование средств, необходимых для передачи полученной информации и выработанного знания (например, кода) другим квантам данной волны, другим структурам и полю (например, появление языка и развитие речи).

16. Разработка моделей новых для контроллера, практически нереальных ранее структур и событий, увеличение их реальности (совершение изобретений).

 Граф структур и событий (особенно, ветвь будущих событий) может быть смоделирован каждым контроллером по разному, в зависимости от той информации, которой обладает контроллер. Ни один контроллер не способен полностью предсказать вид графа будущих структур и событий, так как сама структура этого графа, в свою очередь, зависит от взаимодействия структур и систем, управляемых контроллерами. При этом оказывается, что неизвестными точно оказываются не только вероятности тех или иных исходов будущих процессов, но количество возможных вариантов.

     Тем более, что, по-видимому, у каждого события, в действительности, может оказаться целый шлейф исходов, которые никогда, или почти никогда, ранее не проявлялись, или проявлялись, но просто неизвестны данному контроллеру. Это связано с тем, что вероятность их реализации при обычных условиях близка к нулю. Среди этих событий могут оказаться и чрезвычайно благоприятные для данной структуры. Контроллер, анализируя потенциальную возможность появления таких событий (например, комбинируя в необычных сочетаниях уже известные процессы), может не только моделировать возможность их реализации, но и предсказать ту цепочку бифуркационных событий, которая  резко повысит вероятность исхода, ранее казавшегося почти невозможным.

17. Здесь становится важной еще одна не указанная нами ранее функция контроллера – выяснение глубинных механизмов, управляющих формированием графа структур и событий, его параметрами, а также наиболее общая классификация как событий, так структур и процессов. В человеческом обществе это называется изучением основных законов природы.

18. Для реализации деятельности, необходимой для выполнения пунктов 16 и 17 оказывается в некоторых случаях необходимой организация создания новых структур. Их включение в процессы, в которых участвует система, управляемая контроллером (для человека это труд), повышает вероятность выживания управляемой системы.  

Создание таких структур из элементов поля превращает гомеостатический стабилизирующий контроллер во внешний контроллер, порождающий новые структуры, кванты и волны.

Полученный вывод свидетельствует о возможности существования иерархии чередующихся порождающих и гомеостатческих контроллеров, а вместе с ними и иерархии порожденных ими структур.

 

Взаимодействие структуры (системы) и поля.

 

 Чаще всего поле структуры (системы)  включает две компоненты

1.    Непрерыную (квазинепрерывную), состоящую обычно при более подробном рассмотрении из огромного количества отдельных квантов, имеющих масштабы меры, значительно более мелкие, чем масштаб меры изучаемой структуры.

2.    Дискретную (квазидискретную), представляющую совокупность структур,  входящих или не входящих в волну данной структуры, либо непосредственно взаимодействующих с изучаемой нами структурой, либо взаимодействующих с нею через непрерывную составляющую поля.

 Опыт научных исследований позволил не только классифицировать неперывные поля, существующие в природе, но и использовать в нашем рассмотрении широчайшим образом развитый математический аппарат, позволиший наряду с экспериментальными данными, получить  в некоторых случаях исчерпывающие данные о фундаментальных непрерывных полях, цементирующих Вселенную и определяющих её целостность. В настоящее время исследование этих полей интенсивно продолжается, делаются все новые и новые открытия. Основными характерными свойствами непрерывной (континуальной) составляющей поля является возможность введения двух физических понятий.

1.    Геометрии непрерывного пространства, описываемого в общем случае непрерывным -мерным многообразием.

2.    .Скалярными, векторными или тензорными потенциалами, зависящими от координат поля и удовлетворяющими некоторым линейным или нелинейным дифференциальным уравнениям в частных производных.

Наличие таких непрерывных потенциалов, существующих в любой точке пространства, определяет взаимодействие континуальной составляющей поля с находящейся в том же пространстве структурой. Экспериментальное или теоретическое определение этих потенциалов  позволяет строить уравнения, описывающие скорости и ускорения перемещения изучаемых структур и их элементов в окружающем пространстве. Именно в этом направлении в настоящее время получены наибольшие научные достижения. Вся классическая механика, квантовая механика, теория относительности, теория поля, теория непрерывных сред, то есть все те достижения человеческой мысли, которые составили основы науки XVI-XX веков, посвящены решению этой проблемы. Одно время казалось, что решение именно этой задачи позволит ученым разрешить все загадки природы.  Однако, как мы видим сейчас, детерминированное взаимодействие классических полей с  расположенными в сформированном ими пространстве структурами, описывает законы природы лишь частично.

Это связано с двумя обстоятельствами.

1)    С приближенностью непрерывного описания квазиконтинуального  поля. В любых континуальных полях – гидродинамических или акустических электромагнитных, сильных или слабых, при более тщательном рассмотрении обнаруживаются некоторые кванты, указывающие на дискретный по своей сути характер  структур, характеризующих поле.

2)    С существованием даже у непрерывных потенциалов многозначности (вихревые и спинорные поля), указывающим исследователям на возможность возникновения бифуркационных событий при взаимодействии поля и погруженных в него структур.

     Потенциалы обычно связаны некоторыми однозначными соотношениями с ускорениями (Ньютоновские потенциалы) и скоростями (потенциалы гидродинамического типа) помещенных в континуальное поле структур.

     В непрерывном поле помещаются не только данная структура или система, являющаяся квантом некоторой обобщённой волны, не только все кванты  обобщенной волны, в которую входит данная структура, но и ряд других структур, взаимодействующих с континуальной компонентой поля.

Поле объекта, выделенного  из окружающей среды, может быть разделено на две части:

a)    ближнее поле, включающее в себя континуальную его часть и расположенные в нем объекты, воздействие которых на  изучаемую нами структуру значительно;

b)    дальнее поле – слабо воздействующее на изучаемую структуру на исследуемом отрезке времени.

Если структура определяется некоторой мерой, то  под ближним полем можно понимать ту часть поля, влияние которой не изменяет меру структуры больше, чем на некоторую величину,  которая может быть первоначально назначена.

Взаимодействие изучаемой системы с другими системами, расположенными в том же пространстве, также может происходить несколькими различными способами.

1.    Во первых, структуры  или системы могут взаимодействовать через континуальную составляющую поля.

2.    Вторым типом взаимодействия является непосредственное взаимодействие структур, объемы, занимаемые которыми в пространстве полностью или частично пересекаются. Это взаимодействие чаще всего оказывается более сильным, чем взаимодействие через континуальную составляющую поля и может во многих случаях привести к появлению новых структур, исчезновению старых, поглощению одной структуры другой, установлению стабильных связей между сложными структурами и другим событиям, в результате которых изменяются количество структур и их тип (одним из наиболее ярких примеров такого взаимодействия является вихре-волновой резонанс). 

3.    Третьим ти.пом взаимодействия изучаемого объекта со структурами, входящими в поле, является взаимодействие  структур  при помощи агентов. Для объяснения этого механизма предположим, что некая структура взаимодействует другой структурой – агентом. В результате этого взаимодействия агент изменяется определенным образом, и эти изменения однозначно, или с некоторой вероятностью свидетельствуют  о произошедшем событии. После этого структура – агент взаимодействует с исследуемой нами структурой . При этом результат такого взаимодействия во многом определяется произошедшим ранее взаимодействием агента с первой структурой. Тем самым мы можем говорить о взаимодействии первой структуры с изучаемой нами структурой при помощи агента.  Если оба взаимодействия  такого типа являются бифуркационными и мера , определяющая структуру – агент мала по сравнению с мерами, определяющими две остальные структуры, то такой тип взаимодействия может иметь информационный характер, структура – агент становится носителем информации о существовании, а, возможно, и местоположении первой структуры..

В случае бифуркационных процессов экспериментальное исследование взаимодействия системы и поля может быть осуществлено по той же схеме, что и для детерминированных. Однако, подобное исследование должно проводиться для нескольких процессов, являющихся квантами одной волны с последующей статистической обработкой полученных результатов и определением бифуркационных событий и их вероятности как предельной относительной частоты встречи тех или иных вариантов развития процессов.

     Значительно сложнее обстоит дело в случае, если исследуется уникальная система. В этом случае можно, например,  воспользоваться фрактальностью системы. То есть изучать статистику ее подсистем, считая, что вся система обладает масштабной инвариантностью и перенося на всю систему в целом, с некоторыми оговорками, статистические закономерности, полученные для некоторого набора подсистем. Этот подход должен быть осуществлен с осторожностью, но его результаты могут иметь даже для уникальных систем значительную предсказательную силу.

     Другим методом, дополняющим первый, может стать использование общих закономерностей, полученных для систем, хотя и не являющихся аналогами данной уникальной системы, но принадлежащими к близким классам.. Динамика таких систем, хотя бы на уровне параметра целого, оказывается во многих случаях подобной, и соотношения, полученные для близкого класса, могут оказаться подобными аналогичным соотношениям для нашей уникальной системы. 

 

Информационное взаимодействие контроллеров системы и поля.

 

Взаимодействие контроллеров кванта и волны.

 

Обобщённая волна, соответствующая данной структуре или системе как кванту,  может полностью или частично входить в ближнее или дальнее поле структуры (системы). Поэтому первоначально остановимся на соотношении функций и ответственности контроллеров волны и кванта. Можно выделить два предельных случая, качественный анализ которых представляет значительный интерес..

1. Случай обобщенной волны, полностью управляемой своим контроллером.. Если такая система  состоит из квантов, то кванты не имеют своих контроллеров, а полностью управляются контроллером волны. Суммарная энтропия – информация волны представляет собой только энтропию-информацию, управляемую контроллером волны. Можно сказать, что такая система (или скорее, структура) обладает абсолютной внутренней жесткостью. Такие жесткие структуры эффективно работают, когда структуре предстоит участвовать в бифуркационных событиях, имеющих небольшое число исходов и для выживания требуется хорошо управляемый из единого центра мощный энергетическй импульс. Однако такого типа структуры оказываются плохо приспособленными к выживанию в быстро меняющемся внешнем поле, требующем рационального выбора из большого числа альтернативных вариантов. В такой ситуации гибель внутренне абсолютно жесткой структуры практически неизбежна. При этом вместе с ней гибнут все её кванты, не приспособленные к самостоятельному существованию. Примерами структур, создаваемых человеком, в какой-то мере близких к волне с внутренне жесткой структурой, являются: армия, фабрика или завод, производящие один вид продукции, первобытная община, древние империи с неограниченной властью императора, тоталитарные фашистские и комунистические государства.

Другим предельным случаем, который будем называть случаем свободной обобщённой волны, является вариант, когда каждый квант существует самостоятельно, независимо от других взаимодействует с внешним полем, а общий контроллер волны отсутствует. К этому случаю, например, относится свободное существование одноклеточных живых организмов при неограниченных запасах пищи. Однако, и этот вариант соотношения контроллеров не является оптимальным во всех случаях существования системы. Если условия взаимодействия структуры с полем изменятся таким образом, что обмен мерой между отдельным квантом и полем становится недостаточным, то неизбежно возникает взаимодействие между квантами, которое в случае отсутствия внешнего контроллера вовсе не всегда будет приводить к сохранению квантов, ранее входивших в свободную волну. Гибель волны в этом случае может произойти за счет гибели большого числа отдельных квантов. Здесь необходимо отметить, что в случае свободной волны само понятие обобщенной волны частично размывается. Мы можем говорить о том, что в том или ином месте пространства присутствует некоторая перечисляемая (конечная) совокупность структур (квантов) данного типа – нечто вроде газа молекул, почти не сталкивающихся между собой.

Более четко различие между свободной волной и внутренне жесткой структурой можно проследить на следующем примере. Пусть мы имеем некоторый квант, входящий в бифуркационное событие, в результате которого возможны два исхода с различными значениями меры, реализация каждого из которых имеет вероятность, равную и . Энтропия будущего такого события равна [6].

 Гомеостатический  контроллер системы  в процессе события реализует одну из возможностей, тем самым приобретается информация, равная энтропии будущего этого события. Предположим далее, что имеется  идентичных  квантов, независимо друг от друга вступающих в бифуркационное событие. Контроллеры каждого из таких квантов действуют независимо. В результате из свободной волны практически идентичных квантов формируется большое количество вариантов волн с различным количеством  структур с двумя значенями меры. Это количество вариантов существенно возрастает, если пометить каждый отдельный квант. Можно раcсчитать вероятности каждого из таких  вариантов и вычислить энтропию события для волны, состоящей из  квантов. Эта энтропия растёт с увеличением числа . Однако, весь парадокс ситуации заключается в том , что с увеличением числа  все больше растет число вариантов, в которых отношение числа квантов, находящихся в первом состоянии, к числу квантов, находящихся во втором состоянии, оказывается близким к отношению первичных вероятностей для отдельного кванта. При этом, чем большее число квантов участвует в данном бифуркацонном событии, тем острее пик, соответсвующий этому отношению вероятностей.  При очень большом числе квантов пик, соответствующий исходам с определенным рспределением вариантов квантов сановится, настолько острым, что этот параметр волны становится главным параметром, относительная  погрешность определения  которого в масштабе волны может быть сделана как угодно малой. В этом смысле свободная волна при все возрастающей внутренней энтропии становится все более детерминированной. Энтропия, которая должна  управляться внешним котроллером оказывается равной нулю. Подробное математическое и логическое исследование этого частного случая может пролить свет на достаточно сложный характер перехода от бесконечной мнимой части оператора действия - энтропии к нулевой - на следующем уровне иерархии. Здесь необходимо сделать и еще одно существенное замечание, фактически наличие большого числа идентичных вступающих в бифуркационное событие свободных квантов, приводя на своем уровне к росту энтропии, на уровне волны определяет почти детерминированное расщепление данной волны на две, то есть определяет почти детерминированное событие на уровне волны.

В свободной волне бифуркационные события квантов порождают детерминированные события для всей волны. Рост энтропии и даже стремление ее к бесконечности в одном масштабе рассмотрения приводит к почти детерминированным процессам с новыми мерами и макроскопическими вероятностями – в другом. При этом мнимая часть оператора действия-энтропии, возрастая до бесконечности, одновременно стремится к нулю на следующем уровне масштабов.

 Рост энтропии – приводит к детерминизму.  При этом происходит  почти детерминированное  расщепление волны на две подволны, меры которых оказываются пропорциональными отношению вероятностей.

По-другому выглядит картина в случае абсолютно жесткого управления со стороны контроллера  волны. Пусть, как и ранее, каждый квант вступает в некое бифуркационное событие с двумя исходами, вероятность первого равна , а второго -. Рассмотрим  теперь   аналогичных квантов, втупающих в некое бифуркационное событие. При этом между поведением квантов во время события существует жёсткая корреляция. Если один из квантов во время события принял некоторое состояние, то и все кванты приняли то же состояние. При этом  полная вероятность для каждого кванта принять то или иное состояние остается прежней, однако управляет всей совокупностью квантов уже контроллер всей волны. Квант потерял свой личный контроллер. Такой случай соответствует жесткой системе и приводит к жесткой передаче функций контроллера каждого кванта контроллеру всей волны. Кванты управляются из единого центра они жестко коррелируют между собой. Жесткая структура переносит бифуркационное событие каждого кванта без изменений на бифуркационное событие всей волны.

Может быть предложена еще одна, наиболее наглядная трактовка  предлагаемых двух случаев. Пусть имеется развилка (бифуркация) дороги. К развилке подъезжает автомобиль, за рулем которого сидит человек.  Автомобиль является нашим квантом. Человек – его контроллером. Вероятность того, что человек поедет по правой дороге, равна , вероятность того, что человек поедет по левой стороне дороги равна .  Энтропия неопределенности будущего события равна  . Контроллер выбрал определенную дорогу и ликвидировал эту неопределенность. Таким образом, величина энтропии- информации, управляемая контроллером кванта равна в данном случае . Теперь предположим, что к развилке дороги прибывает одновременно или с некоторым небольшим интервалом  автомобилей, управляемых людьми - контроллерами. Каждый из людей, независимо друг от друга, однако с одинаковой вероятностью, выбирает определенное направление. Количество возможных вариантов выбора системой автомобилей – квантов с водителями - контроллерами растет в степенной зависимости от числа квантов, одновремено пропорционально их числу растет энтропия будущего этого события. При этом энтропия будущего при стремлении числа автомобилей к бесконечности стремится к своему максимальному значению. Но, о чудо! С увеличением числа автомобилей с точки зрения внешнего наблюдателя поток автомобилей становится всё более и более детерминированным. По правой дороге  практически движется число автомобилей, определяемое произведением их общего числа на вероятность каждого из них повернуть в эту сторону. Аналогичная картина наблюдается и по левой стороне развилки. Огромное количество информации, практически равное максимальной энтропии системы автомобилей при каждой реализации того или  иного варианта реализуется контроллерами отдельных автомобилей. Однако со стороны  внешнего наблюдателя почти все эти варианты вследствие идентичности автомобилей выглядят одинаково. В масштабе волны возникают новые, практически детерминированные структуры – потоки машин, меры которых – количество машин – становятся в пределе детерминированными и равными произведениям общего количества машин на вероятность реализации соответствующего пути любой из машин.  Информация от каждого кванта доходит до волны в виде почти детерминированного потока расщепленного на два подпотока, величина каждого из которых равна в каком-то приближении , относительная точность размеров которого увеличивается с увеличением  числа автомобилей, участвующих в бифуркационном событии.

Этим объясняется тот факт, что предложенный нами для детерминированных процессов алгоритм изучения их взаимодействия может во многих случаях оказаться вполне приемлемым и для бифуркационных процессов, энтропия событий которых на микроуровне оказывается очень большой, но на макровременном уровне средние значения параметров взаимодействия процессов оказываются практически детерминированными.

Теперь предположим, что все автомобили поставлены на платформы и весь этот поезд управляется одним водителем. Вновь поезд подходит к развилке дороги и машинист  может выбрать направление дальнейшей дороги с вероятностями  и  .

Однако, если направление уже выбрано, то весь поезд пойдет именно  по этому  пути.

Оба предельных случая взаимодействия контроллеров не могут быть оптимальными для одновременного выживания обобщенных волн и их квантов. Это значит также, что оптимальными соотношениями должны быть некоторые резонансные связи между контроллерами кванта и волны, обеспечивающие все растущую выживаемость как каждого из квантов, так и волны в целом.  Итак, мы вновь получаем здесь не линейную зависимость, а необходимость резонанса или многих связанных между собой резонансов. Именно их поиском занимается Природа, создавая все более сложные совокупности квантов и их иерархии.

2. Выйдем из линейного противопоставления абсолютно жесткой структуры и свободной волны и посмотрим, что приготовила нам природа с целью обеспечить выживание обобщенных волн и структур. Первым из таких сюрпризов является  размножение. Остановимся первоначально на размножении делением. Размножение тождественных или почти тождественных объектов (квантов) осуществляется за счет специальных порождающих контроллеров (для живых объектов это их геном, который одновременно порождает и систему квантов и составляемую ими обобщенную волну). Для каждого кванта его размножение является существенным повышением той информации, которой он владеет, так как при этом вместо одной структуры появляются две идентичных, а уничтожение их обеих становится более проблематичным. Тем самым размножение существенно увеличивает информацию о существовании структуры и её контроллера. В случае гибели одной из структур, появившихся в процессе размножения, она легко в рамках волны может быть заменена ее двойником. Тем самым, увеличивается и выживаемость всей волны. Одновременно вместо одного контроллера волна приобретает два контроллера, каждый из которых управляет определенным объемом энтропии-информации. Суммарное количество энтропии-информации, управляемое контроллерами волны, увеличивается вдвое.

3.Включение в анализ размножения позволяет по-новому подойти к противопоставлению двух предельных случаев взаимодействия контроллеров кванта и волны. Структуры, обладающие способностью к размножению, имеют преимущество в смысле выживаемости перед любыми другими структурами. Однако, размножение требует, наряду с гомеостатическими контроллерами кванта и волны, появления нового типа контроллера – порождающего, который является общим как для кванта , так и для волны в целом. Кстати, именно он в действительности должен порождать оба гомеостатических контроллера. Появляется новая триада, обеспечивающая существенное увеличение выживаемости обобщенной волны и увеличивающая информацию о каждом из её идентичных квантов.

.

                                                      Порождающий

Контроллер                                   /                      \

                      Гомеостатический Кванта-Гомеостатический Волны

 

 Однако, в этом рассуждении кроется и существенное противоречие. Если идентичных квантов становится много, то для гомеостатического контроллера волны информационная ценность каждого отдельного кванта становится меньше и он уменьшает степень защиты этого кванта. Тем самым, в стандартном случае, казалось бы безоговорчный выигрыш в выживаемости имеет свою оборотную сторону.

4. Как мы уже указывали, порождающий контроллер содержит в той или иной форме, чаще всего в форме кода, информацию о будущей структуре (кванте) и её функционировании. При этом в общем случае динамика порождаемой структуры не может быть предсказана однозначно. Структура должна участвовать в бифуркационных событиях и тем самым иметь гомеостатический контроллер. Этот гомеостатический контроллер должен быть спроектирован и реализован в процессе порождения и формирования кванта также на основании кода, заложенного в порождающий контроллер. При этом либо одним и тем же контроллером порождаются несколько квантов, либо каждый квант порождается своим контроллером, однако эти порождающие контроллеры идентичны или почти идентичны. Таким образом, порождающий контроллер (или идентичные порождющие контроллеры) обычно порождают не один квант, а всю волну. С другой стороны взаимодействие гомеостатических контроллеров кванта и волны определяет как поведение самих квантов, так и волны в целом. Кроме того, функционирование обоих контроллеров изменяет не только квант и волну и их поведение, но и окружающее поле, воздействуя в том числе и на контроллер поля. Поэтому возможна хотя и слабая, но длительно действующая обратная связь, в результате которой постепенно изменяется и сам порождающий контроллер. Это, в свою очередь, приводит к качественному изменению как отдельных квантов, так и волны в целом. Существует еще один тип связи между гомеостатическими и порождающими контроллерами. Дело в том, что в некоторых случаях возможно, как это происходит у человека, что гомеостатический контроллер, прямо или косвенно, порождает новые структуры, в том числе может порождать и их гомеостатические контроллеры. Тем самым, возникает не триада, а спиральная цепочка триад, где на каждом уровне происходит смена гомеостатического контроллера на порождающий, но уже в других волнах и квантах.

Возникает интересный вопрос – а может ли эта спираль замкнуться в тор?  То есть, может ли цепочка контроллеров вернуться к своему началу? Может ли стабилизирующий контроллер воссоздать порождающий контроллер, создавший его?

Ответ на этот вопрос – прнципиален. Если да, то человек искусственным способом может создать человека, и не только его.  Мы пока не знаем ответа на данный вопрос, но не исключено, что он будет положительным, и тогда человек возьмет  на себя функции Бога. Есть ли в природе запрет на такую временную цикличность или она является основным законом природы? К этой же проблеме относится и вопрос о замкнутости времени.

5. Вернемся к некоторым другим следствиям из нашего рассмотрения. Возможность порождения новых квантов существенно  меняет динамику волны  и окружающего ее поля. Ведь неограниченное размножение квантов меняет структуру поля и вызывает ответную реакцию, которая может послужить причиной гибели волны. Возможна и другая реакция – количество гибнущих квантов становится равным количеству рождающихся. В этом случае можно сказать, что волна стабилизируется - однако, это состояние иногда оказывается неустойчивым и любые изменения внешних условий могут привести либо к разрушению волны, либо к новому резкому увеличению числа квантов, которое опять-таки может оказаться катастрофическим.

     И здесь возникает новая задача перед контроллерами кванта и волны - либо обеспечить стабильность этого стационарного состояния – либо  обеспечить управляемый рост как числа квантов, так и безопасности каждого из них. Решение этой задачи зависит  от сложности гомеосатических контроллеров (то есть от количества энтропии–информации, перерабатываемой гомеостатическими контроллерами.). При этом естественно появляется четкий критерий для соотношения энтропий-информаций, управляемых контроллерами и кванта и волны – они обе должны быть как можно больше и расти совместно.

6.Однако, Природа придумала еще один важный и интересный прием рождения новых структур, следовательно и формирования их контроллеров. Этот способ объединяет  способы объединения квантов и перезамыкания границ волны. При этом наряду с квантами и содержащей их обобщенной волной формируются новые структуры двух типов – структуры , соединяющие несколько квантов и в связи с этим обладающие новыми бифуркационными и динамическими свойствами, и структуры, имеющие масштаб, меньший, чем масштаб волны, и включающие в себя не только кванты волны, но и ряд подструктур окружающего поля. Такие новые структуры в силу способа их образования относятся, в соответствии с нашей классификацией, к структурам вихревого или мультипольного типа. При этом формирование как структур первого, так и структур второго типа носит фрактальный характер,  то есть в первом случае формируется иерархия структур, объединяющих все большее количество квантов и обладающих своими уникальными свойствами, а во втором случае за счет иерархического процесса неустойчивости границ формируются новые структуры все меньших  и меньших размеров. Оба указанных процесса могут затухать и вновь образовавшиеся структуры быстро исчезнуть, приведя к росту энтропии, не управдяемой контроллерами кванта и волны. Именно эти возникающие и быстро затухающие новые структуры и являются, на наш взгляд основной причиной того, что в мезамасштабах, где действие контроллеров кванта и волны не эффективно, оказывается справедлив второй закон термодинамики - практически мы постоянно имеем состояние происходящего события - энтропия неопределенности структур растет до своих максимальных размеров. Мера неопределенным образом передается из больших масштабов к меньшим. Однако, это происходит не всегда. Иногда возникают такие обстоятельства, что иерархические процессы,  происходящие от кванта и волны, доходят друг до друга и вступают в резонансное взаимодействие, создавая  новые устойчивые резонансные структуры, во многом более устойчивые, чем сформировавшие их квант и волна. Наиболее интересным примером такого рода может служить формирование многоклеточных организмов, имеющих масштабы, промежуточные между клеткой и биосферой. Человек и человечество также является примерами такой резонансной структуры.

Здесь необходимо сделать некоторые замечания. Во-первых, о предпочтительных масштабах таких  резонансных процессов и структур.  Некоторые предположения могут быть сделаны на основании имеющихся эмпирическх данных. Ранее мы указывали на то, что часто наблюдается иерархия соотношений квант-волна. Эта иерархия обладает квазифрактальным свойством, а именно, соотношение мер (например, масс) в этих иерархических цепочках представляет иногда очень большие величины приблизительно одного порядка. Отсюда, можно предположить, и это предположение потребует затем более строгого доказательства, что резонансными оказываются структуры, квадрат меры которых приблизительно равен производению мер кванта и волны, то есть структуры,  которые оказываются волнами меньшего масштаба для сформировавших их квантов, и квантами более крупного масштаба для волны, явившейся их прародителем. Если эту гипотезу удастся обосновать теоретически, то она станет еще одним фундаметальным законом природы, объясняющим фрактальность окружающего нас Мира, да и нас самих. Такая попытка осуществлена в [5].

Так как появление такого рода резонансов, по-видимому, является результатом двух фрактальных цепочек структуроформироваиия, то, появившись, эти  резонансные структуры вновь стимулируют  образование двух новых типов резонансных структур, лежащих между первичными квантами и вновь появившимися резонансами и между вновь появившимися резонансами и  первоначальной волной. Этот процесс может продолжаться достаточно долго и формирует различные типы промежуточных иерархических структур между первоначальным квантом и первоначальной волной. На каждом уровне иерархии существует некоторое количество более не менее идентичных структур, то есть формируется иерархия субволн и суперквантов. В простейшем случае между количествами и мерами  суперквантов устанавливается следущее соотношение, число суперквантов, находящихся в первичной волне, умноженное на величину их меры, есть величина постоянная и равная числу квантов в первичной волне. Этот результат соответствует предложенной автором модели идеального трансформера и близок к большому числу эмпирических данных для сложных иерархических систем, состоящих из большого числа элементов с различной мерой. Возможно, здесь находится также объяснение известного эмпирического факта, состоящего в том, что основными статистическими рапределениями в иерархических системах являются степенные распределения [10, 33]  . В  указанной выше работе показано также, что из дополнительных  резонансных соображений могут быть найдены также и минимальные коэффициенты пропорциональности между мерами и числом членов иерархии, которые оказываются близкими либо к числу 2, либо к числу 1.6180339..., называемому золотым сечением. Не зря это число называется многими символом гармонии.[71-77] В действительности, вследствие неоднородности квантов, а также внешних воздействий формирование  иерархической цепочки происходит часто со значительными отклонениями от простого гиперболического закона.  Попытки абстрактного анализа таких возможных отклоненй были выполнены в работах В. Л. Смирнова.[76 ] . Для математического обоснования возможности такого рода масштабных резонансов нами был  более подробно рассмотрен вопрос о переходе со второго уровня иерархии математических исследований на третий.

 Рассмотрим простейший случай, который может стать моделью общего анализа. Пусть между квантом и сформировавшейся волной появилась лишь одна резонансная структура  промежуточного по мере масштаба, которая может участвовать в собственных бифуркационных процессах. Тогда наряду с контроллерами  кванта и волны возникает новый контроллер этой резонансной структуры, а увеличение количества контроллеров может (хотя и не всегда) привести к увеличению  энтропии – информации, перерабатываемой каждым из них и той части энтропии-информации, которая может быть передана с одного уровня иерархии на другой. Появление такой возможности может увеличить энтропию – информацию, перерабатываемую на каждом уровне иерархии, что резко увеличивает безопасность системы за счет получения возможности делегировать управляющие функции в нужный момент на тот уровень иерархии, на котором наблюдается максимальная опасность для системы в целом. Однако иерархичность сама по себе не является панацеей, автоматически обеспечивающей оптимальное распределение управляющих функций между контроллерами, расположенными на различных уровнях иерархии. Между ними может возникнуть конкурентная борьба за управление (власть), которая может привести к подавлению одним из контроллеров всех остальных  и вновь, на  новом уровне, к жесткой детерминированной структуре, где промежуточные контролеры станут прямыми проводниками воли центра. Возможны и другие варианты, когда промежуточные контроллеры получат  в управление большое количество энтропии информации и единая волна станет свободной волной, однако состоящей не из отдельных квантов, а из практически независимых бывших ранее промежуточными резонансных структур. Процессы такого рода непрерывно идут в иерархических транспортно-информационных системах. Тем самым, создав иерархию масштабов элементов натуральных систем, Природа поставила перед каждой из них проблему выживания – то есть проблему оптимального в данных условиях распределения  управляющих функций между возникащими и существующими подструктурами и их контроллерами.

7. Эта проблема решается всюду по-разному, однако можно высказать один принцип, который можно считать бесспорным. Выживают и живут долго те иерархические системы, которые обеспечивают своим квантам и подсистемам оптимальный для них уровень обмена мерой между собой и с окружающим полем и оптимальное распределение информации и управляющих характеристик между контроллерами различных квантов и уровней иерархии. Оптимальность определяется обеспечением максимальной возможности скорости роста энтропии-информации, управляемой всеми контроллерами системы.

Если такой рост прекращается, то система стабилизируется, что приводит к нарастанию внутренних противоречий между её контроллерами и снижению управляемой системой энтропии- информации, а затем деградации системы и ее гибели от внутренних противоречий  либо от резкого изменения условий  поля, которым не может противостоять совокупность контроллеров системы.

8. Наличие у кванта широких возможностей для выбора вариантов поведения может привести к тому, что разные кванты, попав в различные внешние условия внутри волны или во внешнем поле, могут реализовать при помощи своих контроллеров различные стратегии поведения. Это, в свою очередь, приводит к дифференциации первоначально идентичных квантов и их конроллеров. За счет этого кванты, обладающие большой величиной энтропии-информации, управлемой контроллером кванта, имеют большие возможности приобретения собственной индивидуальности. Отсюда возрастает их информационная ценность как для контроллера волны, так и для контроллеров других квантов. При этом, однако, ввиду идентичности большого объема информации, перерабатываемой каждым отдельным контроллером, преимущества идентичности продолжают сохраняться. Таким образом, вырабатывается оптимальное для данных условий существования соотношение идентичности и индивидуальности, позволяющее воспользоваться преимуществами того и другого с целью выживания за счет увеличения энтропии- информации, перерабатываемой как контроллером кванта, так и всей волны в целом.

9. Наиболее четко такая дифференциация квантов-клеток, управляемая порождающим контроллером – геномом прослеживается в организмах растений и животных, в частности, в организме человека (как обобщенной волны). Однако такое же расщепление квантов-людей в волне – человеческом обществе частично унаследовано от прачеловека и, существенно меняясь, наблюдается в течение всего времени существовния человечества как вида. Именно это расщепление является одной из причин формирования  иерархии промежуточных резонансных структур и соответствующих им динамических процессов между квантом-человеком и волной-человечеством. Дифференциация людей может играть в этих процессах как структурообразующую так и структуроразрушающую роль, в зависимости от внешних условий и степени дифференциации.

10 . Дифференциация квантов существенно влияет на их непосредственное взаимодействие. При этом возможны все элементы спектра взаимодействий от полного слияния в новую структуру до взаимного уничтожения. Наиболее ярко демонстрируют различные варианты взаимодействия структур элементарные частицы.. Оптимальным с точки зрения совместного выживания является такой тип взаимодействия, который, сохраняя оба кванта и повышая их выживаемость, позволяет одновременно увеличить степень идентичности квантов и величину их индивидуальности. Это становится возможным за счет  увеличения величин  энтропии-информации, контролируемой каждым из них при одновременном появлении у каждого кванта новых возможностей, отличных от партнера взаимодействия.

 

Взаимодействие контроллеров структуры и поля.

 

Процессы, происходящие в поле, окружающем исследуемую структуру, вовсе не всегда бывают детерминированными. Если вспомнить, что в общем случае поле, окружающее структуру, включает в себя все объекты Вселенной, то бифуркационный характер событий происходящих в поле изучаемой нами  структуры, становится очевидным. Во Вселенной, включающей в себя  все объекты различных пространственных масштабов и масштабов времени существования, должна возникнуть и развиваться вместе с ней иерархия контроллеров, связанных между собой и управляющих динамикой структур Вселенной, участвующих в бифуркационных процессах.  В случае расщепления поля изучаемой нами структуры на ближнее и дальнее, в ближнем поле , если его непрерывная и дискретная компоненты участвуют в бифуркационных процессах, существует свой контроллер, обеспечивающий его существование.

Так как обычно  хотя-бы часть волны , соответствующей данной структуре как кванту,

входит в ближнее поле, то все, что было сказано по этому поводу ранее, частично относится и к взаимодействию контроллеров ближнего поля и изучаемой нами структуры. Однако ближнее поле

обычно бывает сложнее, чем волна, соответствующая структуре, рассматриваемой как квант.

Кроме того, с данным ближним полем взаимодействуют и другие структуры, которые также участвуют в бифуркационных событиях, но не являются квантами волны, в которую входит наша структура. Эти объекты с необходимостью также имеют свои контроллеры, которые управляют динамикой этих структур, взаимодействуют с контроллером (ами) непрерывной составляющей поля, а также с контроллером самой структуры.  Эти разнообразные типы взаимодействия происходят

1)    за счет обмена информацией о текущем состоянии процессов взаимодействия между структурой и ее полем;

2)    за счет передачи кодированной информации о характере прохождения бифуркационных процессов взаимодействия в прошлом.

3)    за счет передачи закодированной информации о возможном поведении  структуры и поля в будущем

4)    за счет конкурентной борьбы контроллеров за управление системой и полем, которая приводит к возникновению одновременно с масштабной и временной иерархией структур и полей, иерархии контроллеров, борющихся между собой за разделение функций управления структуры и поля.

     Основными средствами взаимодействия контроллеров являются информационные коды, описывающие прошлые, текущие и будущие события. Наиболее удобными  носителями таких кодов являются  структуры – агенты, реализуемые в виде непрерывных волновых мод либо структур, способных участвовать в бифуркационных событиях и взаимодействующие как с полем, так и со структурой. При этом наиболее эффективными из них являются структуры и волны,  имеющие меру, их определяющую, значительно меньшую, чем мера изучаемой нами структуры.

Тем самым непосредственное взаимодействие с таким агентом слабо изменит динамику структуры, однако может существенно повлиять на функционирование контроллера, а уже через него на выбор того или иного сценария в поведении управляемой контроллером структуры.

 

 

Этюд 39.

Взаимодействие бифуркационных процессов.

 

Бифуркационный процесс, соответствующий данной структуре.

 

Все три рассмотренные ранее типа взаимодействия:

а) взаимодействие контроллера и структуры,

б) взаимодействие структуры и ближнего поля,

в) взаимодействие контроллеров ближнего поля и структуры

являются частью взаимодействия ближнего поля и структуры, то есть полного бифуркационного процесса взаимодействия  сложной самоорганизующейся системы с её ближним полем с учётом распределения между ними управляющего воздействия. 

В этот процесс оказываются вовлечены не только изучаемая нами система и ее континуальное ближнее поле с управляющими  контроллерами, но и все системы (структуры), которые функционируют в этом континуальном ближнем поле. При этом, однако, каждая из таких систем (структур) имеет свой контроллер и свое ближнее поле, которое лишь частично совпадает с ближним полем исследуемой нами структуры. Для того, чтобы описать процесс взаимодействия нашей системы (структуры) с другими системами, необходимо параллельно с описанием нашей системы и континуальной части её ближнего поля описывать также информационно- динамический процесс взаимодействия со своим ближним полем всех структур (систем), расположенных в ближнем поле данной системы.

Если такой процесс продолжать последовательно, то он может стать бесконечным, так как мы последовательно будем включать в рассмотрение все новые и новые области непрерывного (квази-непрерывного) пространства  и все новые и новые системы. Строго говоря, приходим к необходимости исследования всей Вселенной и всего графа структур и событий, структурная проекция которого теперь уже погружена в некоторое континуальное -мерное многообразие.

Чтобы избежать этого, можно поступить следующим образом.

Наряду с континуальным ближним полем изучаемой структуры или системы можно ввести сверх - ближнее поле, то есть тот участок ближнего поля, в котором никаких дискретных систем, кроме нашей, не существует. В случае же, если основная мера структуры размыта по континуальному ближнему полю и то же происходит с другими структурами, то можно рассчитать положение определенных точек в -мерном многообразии, являющихся центрами меры нашей структуры и других структур, входящих в ближнее поле, и выбрать область сверх - ближнего поля таким образом, чтобы ни один из таких центров, кроме центра нашей структуры, в него не входил.

Иногда  системы (структуры) сближаются настолько, что расстояния  между их центрами меры оказываются меньше некоторого эффективного размера изучаемой нами структуры. В этом случае можно говорить о непосредственном взаимодействии структур, в результате которого может либо измениться тип каждой из них, либо появятся  новые или исчезнут старые структуры. Этот процесс может оказаться как детерминированным, что бывает реже, так и бифуркационным.

Таким образом, при более подробном, чем ранее, рассмотрении, введя континуальную составляющую поля и геометрию - мерного многообразия, в котором структура взаимодействует с полем, мы получили одно из возможных условий, определяющих приближение, а возможно и свершение того процесса, который ранее был назван нами бифуркационным событием. А именно, во многих случаях условием свершения бифуркационного события является сближение взаимодействующих структур на такое расстояние, что невозможно выделить у каждой из них сверх-ближнего поля. Этот случай является наиболее интересным для анализа механизма прохождения бифуркационного взаимодействия структур и систем, и его изучение позволяет вскрыть глубинные причины бифуркационных событий и классифицировать их в случае взаимодействия двух или нескольких структур, как это было сделано нами в случае классификации бифуркационных трансформаций изолированных волн, вихрей и грибовидных структур. Интенсивно изучаемые в настоящее время методами динамики сплошных сред процессы взаимодействия между собой солитонов, ударных волн и границ, вихревых процессов, грибовидных и мультипольных структур обнаруживают всё новые и новые закономерности этих процессов, моделируемых при изучении взаимодействия особых областей комплексных дифференцируемых многообразий.

 Наиболее характерными процессами такого рода являются резонансные процессы, в частности, описанный нами выше вихре - волновой резонанс.

Однако, вернемся к тому случаю общего положения, когда около каждой из структур, взаимодействующих между собой в пространстве ближнего к ним поля,  можно выделить в каждый момент времени некоторое сверх - ближнее поле, в котором отсутствует какая –либо другая структура , кроме исследуемой. Теперь мы можем дать новую, более глубокую интерпретацию введенному нами ранее графу структур и событий.

Вся структурная проекция этого графа может быть погружена в   мерное многообразие, одной из координат которого является время, а остальные  координат формируют в каждый момент времени некоторое  мерное многообразие , соответствующее геометрии пространства , в котором взаимодействуют между собой структуры и окружающие их поля.

 В качестве структурной проекции графа мы получаем некоторое  мерное многообразие, напоминающее сеть с нитями конечной «толщины», скорее канатами или струнами, или сеть с имеющими некоторый «объем» сечения нитями , вложенное в уже упомянутое  мерное пространство. При этом сечениями канатов или нитей являются геометрические - мерные многообразия, соответствующие тем или иным структурам и их сверх - ближним полям. Этот подход является в какой-то мере обобщением теории струн в квантовой теории поля. 

Будем называть, как и прежде, это странное ветвящееся  мерное многообразие структурной проекцией графа структур и событий. Однако, в отличие от предыдущего рассмотрения, здесь, в этой более подробной модели уже можно учесть то, что не было рассмотрено нами ранее, а именно взаимодействие структур с непрерывной компонентой окружающего их поля. Кроме того, можно более глубоко заглянуть в механизм непосредственного  взаимодействия структур и систем, интерпретируя взаимодействие как перезамыкание границ сверх -ближних полей структур и систем.

Дадим более детальное определение понятия бифуркационного процесса.

Процессом, в который включена исследуемая нами система (структура), будем называть часть структурной проекции графа структур и событий, включающая в себя  некоторую часть траектории в   мерном геометрическом пространстве данной системы (структуры) , под которой понимается некоторое многообразие, которое мы будем называть  по аналогии с теорией динамических систем «мировой линией» структуры совместно со сверх - ближним полем, а также «мировую линию» в том же многообразии континуальной части ближнего поля исследуемой нами структуры с включенными в нее «мировыми линиями» других структур (систем), расположенных в ближнем поле нашей структуры. При этом под «мировыми линиями» этих структур так же как и «мировой линией»  нашей структуры, понимается «мировая линия» самой структуры с её сверх - ближним полем.

Если структура участвует в бифуркационных событиях, то описание процесса становится неоднозначным и необходимо рассматривать несколько ( а возможно, и бесконечное число) возможных процессов, соответствующих динамике нашей структуры.

Назовем эту совокупность процессов – бифуркационным процессом, соответствующим данной структуре.

Подчеркнем  еще раз основной принцип, заложенный в наше рассмотрение. Мы ориентируемся на систему или на структуру как на первичное, что есть в окружающем нас мире. Именно со структурами или системами происходят всевозможные процессы. Именно структуры или системы взаимодействуют между собой и стремятся сохраниться при всех происходящих с ними процессах. Процессы характеризуют динамику изменения структур или систем, их рождения и гибели. Если структуры нет, то нет процесса, с ней связанного.

Для геометрического описания бифуркационного процесса дополнительно к мерному геометрическому пространству , описывающему структурную проекцию модифицированного нами таким образом графа  структур и событий необходимо добавить, как это мы делали ранее, еще и бифуркационную координату, которая, в свою очередь, может представлять собой либо дискретное множество точек, либо счетное их множество, либо одномерную континуальную ось, либо некоторое абстрактное множество.

     Рассмотренные выше определения позволяют для каждой изучаемой структуры (совместно с её контроллером и ближним полем) ввести для заданного промежутка времени как понятие однозначно реализованного процесса, так и бифуркационного процесса, то есть совокупности всех процессов, которые могли бы быть реализованы как в прошлом, так и в будущем на временном отрезке данного процесса, в случае если в некоторый нулевой момент времени состояние структуры, её контроллера и поля известны.

Если конкретная реализация бифуркационного процесса данной структуры представляет вытянутое вдоль оси времени трубчатое мерное многообразие, сечением которого в каждый момент времени является геометрическое многообразие, соответствующее ближнему полю данной структуры, то соответствующий бифуркационный процесс представляет уже многообразие с большей размерностью.  Эту новую размерность даёт бифуркационная координата.

Для каждой структурной реализации бифуркационного процесса можно ввести некоторое - мерное трубчатое ветвящееся многообразие, являющееся совокупностью границ ближнего поля нашей структуры на отрезке времени, определяющем бифуркационный процесс, соответствующий данной системе (структуре). В объёме, ограниченном этой границей существует еще как минимум, два типа трубчатых ветвящихся объемов,.

1.Первый из них – это определенная нами ранее «мировая линия» , соответствующая изучаемой структуре и ее сверхближнему полю.

2. Второй (или точнее – вторые) – это «мировые линии» других структур, находящихся в ближнем поле изучаемой нами структуры.

     При этом «мировая линия», соответствующая исследуемой структуре, находится в «центре» процесса – процесс как бы «надет» на нее. Она является «стержневой» нитью каната . Но в канате- процессе присутствуют другие нити – «мировые линии» других структур. Эти нити – «мировые линии» могут входить в процесс –канат, и выходить из него, при этом сам процесс вхождения и выхода может быть плавным и скачкообразным, детерминированным и бифуркационным.

     Однако, выделив тот или иной конкретный процесс, мы пренебрегаем всей той частью поля структуры, которая, как мы считаем, лежит вне данного процесса . Именно из этого поля входят в процесс новые структуры или системы. Но так как мы исследуем только наш процесс, то мы не можем знать когда, как и какая  новая структура попадет в исследуемый нами процесс. Не зависимо от того, попадает ли в поле нашего зрения, новая структура детерминированным или бифуркационным образом, для нас как исследователей появление новых входящих в процесс структур является на нашем уровне рассмотрения непредсказуемым заранее явлением – то есть таким явлением, которое называют словом – «случайное».  Именно такие – «случайные» явления могут оказаться наиболее опасными для изучаемой нами структуры, именно  для предварительного анализа возможности появления в ближнем поле структур, несущих опасность для нашей и необходимо исследовать не только взаимодействие структур и систем в рамках единичного процесса, связанного с данной структурой, а изучать взаимодействие в более широком контексте, который мы будем называть взаимодействием бифуркационных процессов.

Так же , как мы построили модель бифуркационного процесса, соответствующего данной системе или структуре, мы можем построить аналогичные бифуркационные процессы для  описания динамики других структур и систем, включенных в мировой граф структур и событий.  Таким образом, многобразие, моделирующее динамику Вселенной   может быть покрыто некоторым покрытием из подпроцессов, соответствующих различным структурам. Если нам удалось бы проанализировать динамику движения структур в каждом из таких подпроцессов, то для каждого из них мы могли бы определить какая  система (структура)  вышла из него и в какой момент времени. А так как у многих из этих процессов их пространства пересекаются, то тем самым можно было бы определить, когда и какие структуры вошли в другие процессы. 

Таким образом, одновременное рассмотрение ряда процессов, соответствующих близким структурам, позволяет принципиально решить проблему неопределенности, связанной с вхождением в тот или иной процесс новых структур, то есть на другом уровне сложности определять тип и время взаимодействия структур, входящих в бифуркационный процесс. Применяя затем к каждому из элементарных процессов, соответствующих определенной структуре, подход, разработанный нами ранее для более простого случая, можно, так же как и ранее, ввести понятие связности процесса и связанности структур. В этом случае внутренняя геометрия связанных между собою структур, вводимая нами по аналогии с предыдущим рассмотрением, накладывается на геометрию поля, формируя новую геометрическую структуру. Обычно , если не существует быстро перемещающихся агентов, то между этими двумя геометриями возникает некая локальная связь и новая геометрия локально накладывается на старую, формируя метрическое пространство иногда даже совпадающее с пространством поля (в случае полной однородности). В случае неполной однородности в новом пространстве появляются новые потенциалы, новые волны и новые структуры. Именно так происходит при формировании материальных макроструктур.

Совсем по другому происходит, если новая геометрия формируется агентами связи, перемещающимися в пространстве поля с большими скоростями. В этом случае новая геометрия строится уже не на локальных связях и соответствие первичной и индуцированной геометрий может стать как угодно сложным. В принципе, при бесконечной скорости агентов связи новая и старая геометрии могут стать абсолютно независимыми друг от друга.

Основной проблемой в реализации описанного подхода является необходимость отыскания среди огромного количества процессов, соответствующих различным структурам, таких, которые с минимальными затратами времени исследователя  снимут хотя бы частично проблему «случайности» вхождения «мировых линий» тех или иных структур в процесс, соответствующий данной структуре или системе.

Фактически, задача состоит в оптимальном с этой точки зрения выборе покрытия  многообразия, соответствующего динамике исследуемых нами структур.

Здесь тоже существуют как минимум два аспекта

-       «аспект соседей»

-       иерархический аспект.

 «аспект соседей».

Если мы рассмотрим  всю совокупность бифуркационных процессов соответствующих структурам с масштабом, примерно аналогичным масштабу нашей структуры, то их можно разделить как минимум , на два класса.

1.    Процессы, пересекающиеся  с нашим процессом, то есть такие процессы, у которых ближнее поле структур, которым они соответствуют, на каком – то промежутке времени пересекаются с нашим процессом.- эти процессы формируют

Ближнее поле данного процесса.

2.    Процессы, не пересекающиеся с данным процессом- формируют

Дальнее поле данного процесса.

Существует еще один класс процессов, лежащий на границе между дальним и ближним полем, зона пересечения которых с нашим процессом мала. Такие процессы могут образовать

Пограничные к данному процессу процессы.

Они же могут рассматриваться как граница между ближним и дальним полями данного процесса.

Именно совместное  исследование указанной совокупности процессов и составляет «аспект соседей» в теории взаимодействия процессов.

-       «иерархический аспект».

-       Иерархический аспект в каком то смысле является обобщением рассмотренного нами ранее взаимодействия кванта и волны.

Всякую совокупность взаимодействующих между собой структур, включая сюда их ближние поля и контроллеры, можно, с большим или меньшим основанием, рассматривать как новую систему или структуру следующего уровня иерархии со своим новым контроллером и новым полем, ближним и дальним.  Ей в соответствие приводится новый процесс, который можно считать процессом более высокого уровня иерархии, чем исследуемый нами. Сопоставление информации об обоих процессах, находящихся на различных ступенях иерархии и использование её для  получения знаний о динамике исследуемой структуры и представляет одну из проблем теории взаимодействия процессов. Здесь можно использовать  идеи  асимптотической математики (метод сращиваемых разложений).

 

Меры взаимодействия процессов.

 

Так как понятие взаимодействия бифуркационных процессов является более сложным, чем понятие взаимодействия структур,  то для его описания требуется несколько параметров

Аспект соседей.

1.Простейшим случаем рассмотрения является случай двух процессов, ближние поля которых не пересекаются в  промежутке времени, общем для обоих рассматриваемых процессов. В этом случае каждый из процессов относится к дальнему полю другого процесса. В первом приближении можно считать, что в этом случае эти процессы не  взаимодействуют вообще. Однако, при более глубоком рассмотрении оказывается, что взаимодействие таких процессов может быть учтено следующим образом. Дальнее поле, в принципе, должно существовать независимо от структур и характеризуется неким потенциалом . Существование структуры и динамика её в ближнем поле оказывает некоторое воздействие на дальнее поле в том числе и в районе расположения структуры, центрирующей взаимодействующие процессы. Эти изменения потенциалов вызывают в свою очередь изменение поведения структур, центрирующих процессы. Тем самым оба процесса изменяются по сравнению с тем гипотетическим случаем, когда центрирующие их структуры отсутствуют. Таким образом, мерой взаимодействия процессов в этом случае является мера, характеризующая динамику изменения потенциалов дальнего для каждого из процессов поля при наличии другого процесса по сравнению с тем случаем, когда внешний процесс отсутствует. Эти изменения могут быть оценены теоретически путем рассмотрения трех случаев.

1.    Анализ первого процесса, проходящего в заданном дальнем поле при отсутствии второго процесса .

2.    Анализ второго процесса, проходящего том же внешнем поле при отсутствии первого.

3.    Совместный анализ динамики обоих процессов.

Изменение параметров процессов в третьем случае по сравнению с двумя первыми – и есть результат взаимодействия.

Если изучается взаимодействие расположенных в ближнем поле друг относительно друга или пограничных процессов, то здесь появляются другие параметры взаимодействия, среди которых первым можно считать абсолютный или относительный объем пересечения процессов как многообразий. Абсолютный объем представляет собой интеграл по времени взаимодействия от объема общего ближнего поля обоих взаимодействующих процессов . Может быть введен также и соответствующий относительный объем, когда эта величина делится на объем одного из взаимодействующих процессов.

В некоторых случаях можно в качестве параметра взаимодействия на этом уровне использовать производную по времени от введенной нами величины. То есть объем ближнего поля, общий для обоих процессов в данный момент времени. Для более подробного анализа взаимодействия процессов может быть использована и вторая производная от объема взаимодействия по времени, характеризующая скорость изменения общего объема ближнего поля обоих процессов.   

Другим, более важным критерием взаимодействия в этом случае является совокупность величин, которые могут быть названы параметрами обмена структур.

1.    Первым из них может считаться объем, занимаемый мировыми линиями структур, располагающихся в той части ближнего поля, которая является общей для обоих взаимодействующих процессов. Это практически величина интеграла от меры (действия) всех структур , расположенных одновременно в ближнем поле обеих структур, центрирующих взаимодействующие процессы. Эта величина характеризует степень общности взаимодействующих процессов. Можно даже ввести приближенный критерий, позволяющий определить, когда оба взаимодействующие процесса практически не могут быть разделены и когда их можно рассматривать как единый целостный процесс. Таким критерием может являться принадлежность «мировых линий» центрирующих структур обоих процессов к общей для обоих процессов части ближнего поля.

2.    При прохождении процессов «мировые линии» различных структур могут выходить из ближнего поля одного процесса и входить в ближнее поле другого процесса, а также  оказаться в  общей части обоих процессов. При этом происходят качественные изменения самих взаимодействующих процессов. Эти изменения интегрально  могут быть характеризованы либо числом структур, перешедших из одного процесса в другой, или вошедших и вышедших из общей части обоих процессов. Если считать что «мировые линии» структур, участвующих во взаимодействии процессов, могут быть измерены одной мерой (в качестве которой можно использовать объем этих мировых линий) , то вместо числа структур,  может быть использована суммарная мера всех структур, вошедших  в один из взаимодействующих процессов (или вышедших из него), либо мера структур, входящих (или выходящих) в общий объем взаимодействующих процессов. Эти параметры должны характеризовать своеобразный «обмен веществ» между  процессами.

 

Так как мы рассматриваем бифуркационные процессы, то некоторые структуры, вышедшие из одного процесса, и перешедшие в  процесс с ним взаимодействующий, одновременно с мерой несут также информацию о бифуркационных процессах, происходивших в недрах процесса, из которого они только что вышли. Взаимодействия с контроллером процесса, в который она только что вошла, структура изменяет вероятность реализации того или иного будущего бифуркационного события. Тем самым каждая «мировая линия», перешедшая из одного процесса в другой, несет с собой не только некоторую меру, но и информационный код о произошедших в соседнем процессе ранее событиях, то есть несет с собой некоторую информацию. Эта информация  воспринимается контроллером процесса и может быть превращена им в «знание», которое позволит ему предсказать варианты взаимодействия процессов в будущем и обеспечить безопасность центрирующей процесс структуры. Некоторые типы структур несут с собой очень малую меру, но очень большой объем информации. Такие структуры могут быть названы информационными.  При наличии таких структур взаимодействие процессов может быть разделено , так же как и взаимодействие структуры и поля (и взаимодействие структур между собой) на материальное (обмен мерами структур) и информационное (обмен информации, которую несут «мировые линии» структур, переходящих из одного процесса в другой).

            

. Иерархический аспект.

 

Взаимодействие процессов , принадлежащих к к различным уровням иерархии носит совершенно иной характер. Здесь существенную роль играет параметр структурных и полевых , а также временных масштабов взаимодействующих процессов. Процесс, находящийся в масштабной иерархии выше,  обычно включает в себя один, несколько или очень много процессов более низкого уровня иерархии, взаимодействующих между собой в соответствии с «аспектом соседей»

При этом необходимо рассматривать два очень сильно различающиеся случая.

1. Процесс низкого уровня иерархии геометрически находится все время внутри процесса, принадлежащего к более высокому уровню иерархии.  В этом случае внешний процесс частично (а иногда и полностью) формирует ближнее и дальнее поле процесса меньшего масштаба. В свою очередь, совокупность взаимодействующих процессов более низкого уровня иерархии формирует меру структуры , центрирующей процесс более высокого уровня иерархии.

В отношении же информационного взаимодействия можно , заменяя слово «контроллер структуры» словом контроллер процесса, где под контроллером процесса можно понимать «мировую линию» контроллера центрирующей его структуры, повторить все рассуждения, которые были выполнены нами при изучении взаимодействия контроллеров кванта и волны и структуры и поля.

      По другому обстоит дело, если процесс более низкого уровня иерархии  находится на границе процесса  более высокого уровня иерархии. Тогда мировая линия центрирующей структуры низкого уровня иерархии  может входить или выходить из мировой линии структуры более высокого уровня иерархии и нести в мир или приносить из мира тот или иной объем информации, практически не влияя на меру основной структуры( и соответствующего ей процесса). Таким образом  граничные процессы малого масштаба становятся чаще всего переносчиками информации для процессов больших масштабов. Это рассуждение еще раз подтверждает существенную роль границ в информационном взаимодействии структур и процессов.

 

1.    Басин М. А. Волновой подход к исследованию структур и систем. Реальность и субъект. Том 2. № 2-3. СПб.: 1998. Сс.57-72.

2.    Арнольд В.И. Авец А. Эргодические проблемы классической механики. Ижевск. Ижевская республиканская типография.1999. 284c.

3. Цишанг Х., Фогт Э., Колдевай Х.Л. Поверхности и разрывные группы. М.: «Наука».1988. 688с.

4. Арнольд В. И. Обыкновенные дифференциальные уравнения. Изд. 3, перераб. и доп. М.: «Наука» 1984. 272с.

5. Басин М. А. К теории идеального трансформера. Синергетика и методы науки.- СПб.: «Наука». 1998. 439с.

6.. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Часть 1. СПб.: «Норма». 2000. 168с.

7.    Хакен Г. Синергетика. М.: «Мир».1980. 408с.

8. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика в 10 томах. Том 3. Квантовая механика. Нерелятивистская теория. Издание четвертое, исправленное при участии Л.П. Питаевского. М.: «Наука» ГРФ-МЛ 1989, 768c.

9.   Колмогоров А.Н. Основные понятия теории вероятностей. М.-Л.: ОНТИ, 1936; Изд.2. М.: Наука,1974; Изд.3. М.: Фазис 1998.130с.  

10. Тейяр де Шарден П. Феномен человека М.:“Наука”.1987. 240с.

11. Милнор. Дж. Голоморфная динамика. Ижевск. НИЦ «Регулярная и хаотическая динамика». 2000, 320 с.

12. Басин М.А. Компьютеры. Вихри. Резонансы: Волновая теория взаимодействия структур  и систем. Часть 2. СПб.: «Норма» 2002 160с. (В печати).

13. Баранцев Р. Г. Системные триады и классификация. Теория и методология биологических классификаций. М.: 1983. С.81-89.

14. Баранцев Р. Г. Системная триада - структурная ячейка синтеза. Системные исследования. Ежегодник 1988. М.:1989. С.193-210.

15.. Баранцев Р.Г. Системная структура классификации. Классификация в современной науке. Новосибирск: 1989. Сс.73-86.

16. Семиодинамика. Труды семинара. Под редакцией Р. Г. Баранцева. СПб.:1994 192 с.

17. Баранцев Р. Г. Открытым системам – открытые методы. Синергетика и методы науки. (Редактор М. А. Басин). СПб.: «Наука».1998. Сс.28-40.

18. Баранцев Р. Г. Концепции современного естествознания: опыт целостного подхода. Методическое пособие для студентов гуманитарных факультетов. СПб.: СпбГУ. Юридический факультет. 2001. 80 с.

19. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. М.: «Наука». 1976. 544с.

20. Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М.: «Наука». 1998. 288с.

21. Постон Т. Стюарт И. Теория катастроф и её приложения. М.: «Мир». 1980. 608с.

Poston T. Stewart I. Catastrophe Theory and its Applications. London-San-Francisco- Melbourne 1978

22. N. Bourbaki  Elements de mathematique. Paris.: Hermann.

23. Шварц Л. Анализ. Том 1. М.: Мир 1972. 824с.

 Schwartz L. Analyse Mathematique. Cours Professe a l’Ecole Politechnique. Paris. Hermann 1967.

24. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложения . М: «Наука» 1986. 760с.

25. Пайтген Х.О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем.М.: «Мир» 1993.176с.

Peitgen H.O. Richter P.H. The Beauty of Fractals. Images of Complex Dynamical Systems. With 184 Figures , Many in Color. Springer -Verlag Berlin-Heidelberg - New-York - Tokyo 1986

26.                        Арнольд В.И. Теория катастроф. Изд. 3-е, доп. - М.: «Наука». 1990.128 с.

27.                        Mandelbrot B. The Fractal Geometry of  Nature  N.-Y.; W.H. Freeman 1982.

28. Лихтенберг А., Либерман М. Регулярная и стохастическая динамика. М.: «Мир» 1984. 528с.

29. Управление риском. Риск. Устойчивое развитие. Синергетика. М.: «Наука» 2000. 431с. (Серия «Кибернетика: неограниченные возможности и возможные ограничения»).

30. Баранцев Р. Г. Явление цвишенизма в социальных кризисах. Синергетика, философия, культура. М.: Издательство Российской академии государственной службы при Президенте Российской Федерации. 2001. Сс. 220-225

31. Режимы с обострением. Эволюция идеи: Законы коэволюции сложных структур. – М. « Наука» 1999. 255с. (Серия «Кибернтика: неограниченные возможности и возможные ограничения»).

32. Басин М.А. Спиральные числа. Степенные особенности. Волны. Вихри. Грибовидные структуры. Транспортно-информационные системы. Международная междисциплинарная научно-практическая конференция: «Современные проблемы науки и образования». Керчь, 27 июня – 4 июля 2001 года. Материалы конференции .Часть1. Харьков: 2001. Сс.12-13. 

33. Иванов - Ростовцев А.Г., Колотило Л.Г., Тарасюк Ю.Ф., Шерстянкин П.П. Самоорганизация и саморегуляция природных систем (модель, метод и основы теории D-SELF (под редакцией, с предисловием, комментариями и заключением академика РАН К.Я.Кондратьева). СПб.: Русское географическое общество, 2001.216 с.  

34. Николис Г., Пригожин И. Познание сложного. Введение. М.:”Мир”.1980.

35. Пригожин И. От существующего к возникающему. Время и сложность в физических науках. М.: «Наука». 1985.

36. Пригожин И. Стенгерс И. Порядок из хаоса. Новый диалог человека с природой.Изд. 2. М.: «Эудиториал УРСС». 2000. 312с.

37.                        Вентцель А.Д. Курс теории случайных процессов.М.: «Наука». 1975 320с.

38.                        Poincare H. Les Methodes Nouvelies de la Mecanique Celeste/-Paris:Gauthier - Villars, 1893

Пуанкаре А. Новые методы небесной механики. Т1,2 Избранные труды .- М.:”Наука”,1971-1972.

39. Grawford F.S. Waves. Berkeley Physics Course,Volume 3, Mc-Graw-Hill Book Company 1967

40. Feynman R.P., Leighton R.B., Sands H., The Feynman Lectures on Physics, V.3, Addison-Wesley Publishing Company, INC, Reading, Massachusetts, Palo Alto, London,1963

41.Краснушкин П.Е. Обычные волны М.: "Физический энциклопедический словарь"1963

42. A Discussion on Nonlinear Theory of Wave Propogation in Dispersive Systems Organized by M.J.Lighthill. Sec.R.S., Published by the Royal Society, London,1967.

43. Нелинейные волны. Самоорганизация . Редакторы: А.В.Гапонов-Грехов , М.И. Рабинович, М.: «Наука». 1983. 264с.

44. Нелинейные волны. Структуры и бифуркации. Редакторы: А.В.Гапонов-Грехов, М.И.Рабинович, М:"Наука',1987

45. Сретенский Л.Н. Теория волновых движений жидкости , М.:"Наука" 1977, 815с.

46. Бхатнагар П. Нелинейные волны в одномерных дисперсных системах.М.:Мир 1983.136с.

Bhatnagar P.I. Nonlinear Waves in One-dimentional Dispersive Systems. Clarendon Press, Oxford,1979.

47. Стокер Дж. Дж. Волны на воде, математическая теория и приложения .М.:ИИЛ,1969, 620 с

.Stoker J.J. Water Waves. The Mathematical Theory with Applications. Interscience Publishers ,Inc., New York , Interscience Publishers Ltd., London,1957

48. Lighthill J. Waves in Fluids. Cambridge University Press. Cambridge, London -New-York-Melbourn,1978.

49. Басин М.А., Шилович И.И. Синергетика и Internet. Путь к Synergonet. СПб.:    Наука.1999.- 71с.

50. Синергетика и методы науки. (Редактор М.А. Басин). СПб.: «Наука».1998. 440c.

51. Арнольд В.И. Математические методы классической механики. М.: «Наука».1974. 432с.

52. Андронов А. А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Физматгиз. 1959.

53. Афраймович В. С. Внутренние бифуркации и кризисы аттракторов. Нелинейные волны . Структуры и бифуркации. М.: Наука.1987. C. 189-213.

54. Басин М. А. Основы классификации нелинейных волновых движений и вихревых структур. Явление вихре - волнового резонанса при движении несимметричных тел в неоднородной жидкости. Проблемы гидромеханики в освоении океана Материалы конференции по прикладной гидромеханике. Киев: ИГМ АНУ. 1992. Сс.192-193.

55. Basin M. A. Wave Formation by the Motion of a Surface Ship Hydrodynamic Complex near the Free Boundary. Classification of Nonlinear Waves. Wave-Vortex Resonance.  Papers of IMAM 93 Congress // Ed. By P.A.Bogdanov. Vol.II. Varna. Bulgaria. 1993. Pp. 51-58.

56. Basin M. A. Foundations of Nonlinear Waves and Vortex Structures Classification. Paper, Presented on the International Symposium:" Nonlinear Oscillations, Waves and Vortexes in Fluids". St.-Petersburg: June 1994.

57. Basin M. A. Wave Methods in the Investigations of Structures and Systems. Moscow Forum of Synergetics, the January 1996 Meeting" The Sustainable Development in Changing World", January 27-31, Moscow: Abstracts. Pp.36-38.

58. Басин М. А. Синергетика - волновой подход к исследованию открытых структур и систем .// Проблемы ноосферы и устойчивого развития. Материалы первой международной конференции. С.-Петербург 9-15 сентября 1996 года. СПб.: Издательство СПб Университета . 1996 . Сс. 104-107.

59. Басин М. А. О влиянии нелинейности и диссипации на формирование структур. Доклад на втором международном философско-культурологическом симпозиуме: ”Размышления о хаосе." 18 апреля 1997.

60. Басин М. А. Основы классификации нелинейных волновых движений, вихрей и транспортных систем.// Синергетика и методы науки.(Ответственный редактор М. А. Басин) СПб.: «Наука».1998. Сс.95-113.

61. Басин М. А., Завадовский Н. Ю. Модель двойного спирального вихря как предельная форма свободной поверхности для нестационарного потока идеальной несжимаемой жидкости. Труды семинара по обратным краевым задачам. Вып. 22. Казань: КГУ. 1985.

62. Басин М. А., Шапошников И. Г. Новая модель нестационарного течения около крыла в невязкой жидкости. Математическое и физическое моделирование в гидродинамике судна. Труды НТО СП . Выпуск 18 Л.: "Судостроение" 1989. Сс.27-38.

63. Арнольд В. И. Особенности каустик и волновых фронтов. М.: «Фазис» 1996. 334 с.

64. Басин М.А., Рудкевич Л.А. Синергетический подход к обоснованию связей между физическими и психическими свойствами человека. Синергетика и психология. Материалы круглого стола 10 марта 1997 года. Санкт-Петербург (Ответственные редакторы М.А. Басин , С.В. Харитонов.) Доклады. СПб: НИЦ “Синергетика ” СПбСУ.1997.Сс 23-39.

65. Филипс О.М. Взаимодействие волн - эволюция идеи.  -Современная гидродинамика , успехи и проблемы .(Редакторы Дж.Бетчелор, Г.Моффат) М.: Мир.1984.Сс. 297-314

66 .Басин М. А. Основные уравнения вихревого движения жидкости. Вихре-волновой резонанс. Материалы по обмену опытом. Труды НТО СП.Л.1990.

67. Basin M. A. Basic Equations of Vortex Fluid Motion. Vortex-Wave .Resonance. IUTAM Symposium on Separated Flows and Jets. Novosibirsk:USSR 1990. Pp39-41 Springer - Verlag. Berlin-Heidelberg 1990. V. V. Kozlov, A.V. Dulov (Editors), Pp.113-116.

68. Басин М. А., Лордкипанидзе А. Н., Ткач А. Я. Решение задачи о стационарном движении несущей поверхности вблизи границы раздела сред. Вихре - волновой резонанс. Труды НТО СП. Вып.1. Л.: 1990. C.115-127.

69. Басин М. А., Лордкипанидзе А. Н. Ткач А. Я. Гидродинамические характеристики несущего комплекса, движущегося вблизи свободной поверхности весомой жидкости. Труды Семинара по краевым задачам. Выпуск 26. Аэродинамика течений с неизвестными границами. Казань: КГУ 1991.С.29-59

70. Басин М. А. Вихре - волновой резонанс. Синергетика и методы науки. (Редактор М. А. Басин). СПб.: «Наука».1998. Сс.415-418.

71. Сороко Э.М. Структурная гармония систем, наука и техника. Минск. 1984. 264c.

72.  Марутаев М.А. О гармонии как закономерности.  Принцип симметрии (Отв. ред. Б.М. Кедров, Н.Ф. Овчинников). М. Наука 1978.

73. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение ( Три взгляда на природу гармонии) М.: «Стройиздат». 1990.

74. Быстров М. В. О шуме 1/f с точки зрения всеобщей гармонии. Синергетика и методы науки. (Отв. ред. М.А.Басин) СПб.: «Наука».1998. Сс. 375-390.

75. Смирнов В.Л. Проблемы логики при моделировании самоорганизующихся структур. Синергетика и методы науки. (Отв. ред. М.А.Басин.) СПб.: «Наука».1998 Сс. 40-63.

76.Смирнов В.Л. Солнечный диск: механизм формирования структуры и начальные этапы эволюции. Синергетика и методы науки.(Отв ред. М.А.Басин) СПб.: «Наука».1998. Сс. 390-410.

 

77. Крылов Ю.К. Кудрин Б.И. Целочисленное аппроксимирование ранговых распределений и идентификация техноценозов. // Ценологические исследования . Одиннадцатый выпуск. М.: Центр системных исследований.1999. 80с

 

 

Синергетика. Этюды 70.

Памяти   наших родителей

Смирновой Полины Викторовны  Басиной Цицилии Рувимовны

Смирнова Ивана Ивановича      Басина Абрама Моисеевича

посвящается

 

Басина Г. И., Басин М. А.

НИЦ «Синергетика» Санкт-Петербургского союза учёных.

 

Этюд.

 

Этюд 40.

Теория Synergonet.

 

В монографиях  [4-5]     М. А. Басиным и И. И. Шиловичем при анализе совместного развития Человечества и Internet было введено понятие Synergonet, сложной самоорганизующейся системы, сочетающей в себе детерминизм компьютерных расчётов и неопределённость поведения массы людей, управляющих расчётами и передачей информации внутри сети. Ими было указано не только на достоинства объединения Человечества и Internet в единую систему, но и на возможные опасности такого объединения. Указанные обстоятельства приводят к необходимости построения теоретических основ динамики развития Synergonet, базирующихся на синергетической методологии анализа сложных самоорганизующихся систем. В монографии [3] нами показано, что такая теория может быть построена на базе нового типа компьютера, названного нами целостным [1] и должна быть единой для всех живых объектов, от вируса до Человечества  и Synergonet. Основы такой теории, названной информационно-волновой, кратко изложены нами в монографиях [2] - [8]. В настоящем этюде мы более подробно останавливаемся на фундаментальных положениях развиваемой теории.

     .Каждая изучаемая человеком или искусственно создаваемая им система в каждый момент времени находится в некотором состоянии, которое может быть математически приближённо описано некоторой совокупностью обобщённых координат. С изменением момента времени система переходит в некоторое новое состояние. Процесс перехода системы с изменением момента времени в некоторое новое состояние будем называть событием. В большинстве неживых систем, подчиняющихся уравнениям динамики Ньютона, обладающих теоретически неограниченным числом непрерывно изменяющихся во времени состояний, переход из одного состояния в другие определяется однозначными функциями. Такие системы могут быть названы детерминированными. К детерминированным системам могут быть отнесены и многие компьютерные программы с фиксированными исходными данными. Те системы, которые мы собираемся рассматривать при создании теории Synergonet, обладают обычно как дискретным спектром с очень большим числом состояний, так и непрерывным. По счастью, описание такого спектра с переходом от одного способа описания к другому было выполнено в теории вероятностей и квантовой механике. Поэтому в дальнейшем мы рассмотрим кажущийся более простым, но на наш взгляд, более общий, так как он не содержит условия непрерывности, случай дискретного спектра состояний, считая, что переход к непрерывному и комбинированному спектрам может быть осуществлён с использованием известных процедур.

     Нас в дальнейшем будут интересовать процессы, отличные от детерминированных, то есть такие, в результате свершения которых, принципиально или в результате ограниченности наших знаний, может осуществляться переход не к одному, определённому однозначно состоянию, а к нескольким альтернативным состояниям. Здесь необходимо ввести представления о процессе кванте и обобщенной волне почти идентичных процессов. У детерминированных процессов результат перехода будет идентичным у всех процессов - квантов, входящих в данную обобщённую волну. Процессы, которые нас интересуют, и которые мы назовём бифуркационными, не обладают таким свойством. Оставляя пока в стороне философский вопрос, существуют ли такие процессы в действительности или мы скрываем за их определением недостаточность наших методов выбора обобщённой волны, соответствующей процессу-кванту, считаем, что такие процессы существуют и составляют основу поведения живых систем и Synergonet.

     В этюде 31 мы ввели представление о бифуркационном событии, то есть таком событии, результат которого не может быть заранее однозначно предсказан, и выяснили, что необходимо ввести понятия события-кванта и события обобщённой волны.

     В результате совершения бифуркационного события-кванта система из заданного состояния переходит в некоторое конкретное состояние, предсказать которое однозначно мы не можем, так как при переходе к другому кванту той же обобщённой волны-события система из того же состояния может перейти в иное состояние. Таких новых состояний может быть два, несколько, бесконечное количество как дискретных, так и непрерывно меняющихся.         Совокупность этих состояний была названа спектром бифуркационного события-обобщённой волны при заданном начальном состоянии.

     При совершении бифуркационного события-кванта система из заданного начального состояния переходит лишь в одно состояние из спектра события - волны. Если повторять события-кванты многократно, то различные результирующие состояния могут повторяться с различной частотой и соотношение этих частот может в пределе стремиться к устойчивым значениям, которые в некоторых случаях можно определить, например, из соображений симметрии. Существование в природе таких устойчивых соотношений позволяет присвоить состояниям спектра бифуркационного события-волны некоторое действительное или комплексное число, каким либо образом связанное с частотой встречи состояния в спектре бифуркационного события - волны.

     Данное определение является обобщением ряда определений, введённых ранее различными авторами при создании теории вероятности, теории случайных процессов, квантовой динамики. Благодаря  своей общности, именно оно наиболее адекватно подходит для исследования различных типов наиболее сложных динамических процессов различной природы.

В настоящем этюде мы вводим понятие бифуркационного процесса как последовательности следующих одно за другим бифуркационных событий.        Рассмотрим, как и ранее, частный случай общего подхода, сближающий его с классической теорией вероятности и теорией случайных процессов. Предположим, что каждому состоянию из конечного спектра состояний бифуркационного процесса-волны присвоено некоторое положительное действительное число, меньшее или равное единице, которое по аналогии с теорией вероятности назовём вероятностью реализации данного состояния при свершении бифуркационного процесса. Обозначим его , где  - номер данного состояния в спектре состояний бифуркационного процесса – волны, всего таких состояний  . Примем, что сумма всех значений  равна единице .

Если считать процессы-кванты независимыми, то аналогично случаю теории вероятности можно показать, что асимптотически при числе процессов – квантов, стремящемся к бесконечности, относительное число реализации  -того состояния стремится к величине. Тем самым абстрактные числа  приобретают некоторый физический смысл. Однако, в отличие от случая теории вероятности, в реальных системах подобное отождествление полностью реализовать не удаётся, поэтому у целостных систем их контроллер либо получает информацию о величинах извне, либо «учится» в процессе существования системы, уточняя значения  после каждого свершившегося процесса-кванта.

     Введение в рассмотрение представления о бифуркационном процессе позволяет по-новому взглянуть на проблему времени. Ось времени в этом случае разделяется на три отрезка. Первый отрезок соответствует времени до свершения данного бифуркационного процесса-кванта. В этот период времени мы в лучшем случае знаем лишь прошлые и исходное состояния и спектр возможных будущих состояний системы и их вероятности. Второй отрезок соответствует  течению бифуркационного процесса. В этот период времени осуществляется выбор одного из спектра возможных состояний, реализуется процесс-квант. В следующий момент времени система готова к свершению следующего бифуркационного процесса.

Применительно к бифуркационному процессу-волне по аналогии с теорией вероятностей может быть введено понятие энтропии бифуркационного процесса, которая определяется по формуле

.

В случае, если процесс имеет только один исход (детерминированный процесс), все значения , кроме одного, равны нулю, а это значение равно единице. Энтропия процесса в этом случае равна нулю. Максимальное значение энтропии  достигается, когда все значения  равны между собой. В момент завершения процесса энтропия обращается в нуль - приобретается новая информация о свершившемся процессе-кванте

 

,

которая может быть затем использована наблюдателем или контроллером системы для уточнения величин  процесса-волны.

Таким образом, бифуркационный процесс обладает всеми свойствами бифуркационного события. Однако он является сложным бифуркационным событием. Возникает вопрос о связи параметров бифуркационного процесса со свойствами входящих в него бифуркационных событий.

Предположим, что бифуркационный процесс состоит из последовательно происходящих бифуркационных событий. Рассмотрим, что происходит до и после первого бифуркационного события. В момент перед свершением этого события система находится в некотором -том состоянии. Вероятность перехода в некоторое -тое состояние . Таким образом, формируется матрица перехода для первого бифуркационного события . После гипотетического перехода к началу второго бифуркационного события вероятность нахождения системы в-том состоянии   .Тем самым мы априори в момент начала бифуркационного процесса знаем вероятности реализации каждого из возможных состояний перед вторым бифуркационным событием. Далее, пусть нам известна матрица вероятностей перехода из одного состояния в другое при совершении второго бифуркационного события . Это означает, что, если система до совершения второго события находилась в-том состоянии, то вероятность её перехода в-тое состояние равняется . Однако, система предположительно перед вторым бифуркационным событием находится в  -том состоянии лишь с вероятностью . Можно  предположить, что вероятность системы оказаться в  - том состоянии, пройдя при этом -тое состояние  . Общая вероятность реализации -того состояния в результате второго события представляет результат смешения по всем . В общем случае это смешение может производиться различными способами. Здесь мы примем простейший способ смешения. Общая вероятность реализации -того состояния равен сумме частных вероятностей.

 .

Таким образом, матрица вероятности перехода от нулевого момента ко второму определяется как произведение матриц первого и второго бифуркационных событий.

Распространяя указанный подход на все события изучаемого процесса, получим, что матрица перехода бифуркационного процесса равна произведению матриц перехода входящих в него бифуркационных событий .Таким образом, зная матрицы перехода всех событий данного бифуркационного процесса можно определить матрицу перехода самого процесса.

Если мы имеем матрицы перехода каких либо событий или процессов, то их произведение также удовлетворяет свойствам матрицы перехода. Таким образом, матрицы перехода формируют полугруппу матриц, сумма элементов которых в каждой строке равна единице. Этим свойством должны обладать все матрицы перехода как для бифуркационных событий, так и для бифуркационных процесов. Единицей этой полугруппы является матрица, диагональные члены которой представляют собой единицы, а остальные – нули. Изменение нумерации состояний системы не меняет сути физических процессов. Поэтому матрицы с переставленными строками и соответствующим образом переставленными столбцами могут считаться эквивалентными. Единичная матрица сохраняет любое наперёд заданное состояние и описывает абсолютный покой. Обратные матрицы не относятся к исследуемой полугруппе. Однако полугруппа обратных матриц также имеет определённый физический смысл. Пусть некоторый процесс или некоторое событие имеет некоторую матрицу перехода, преобразующую вектор вероятности в начальный момент времени  в вектор вероятности в конечный момент времени, Тогда обратная матрица преобразует вектор вероятности в конечный момент в вектор вероятности в начальный момент. В связи с этим интерес представляет определитель матрицы перехода. Определитель единичной матрицы равен единице. Как показал анализ матриц перехода второго порядка, он меняется от минус единицы  до плюс единицы , проходя через нуль [3].  Можно предположить, что этим же свойством обладает совокупность матриц перехода любого порядка.  Если определитель матрицы перехода равняется нулю, что происходит, например, в случае, когда две строки матрицы перехода равны между собой, то определитель обратной матрицы стремится к бесконечности. Это означает, что в этом случае по распределению вероятностей в конечный момент времени нельзя однозначно определить распределение вероятности реализации состояний в начальный момент.

Особую роль среди бифуркационных процессов играют процессы, которые могут быть названы квази - стационарными. У этих процессов матрица перехода для всех входящих в процесс событий постоянна и не зависит от номера события. В этом случае, если определитель матрицы перехода для события меньше единицы, то при повторении событий определитель процесса стремится к нулю и возрастает неопределенность в определении начального состояния по конечному.  

Теперь рассмотрим другую проблему. Пусть нам задана матрица перехода для какого-либо бифуркационного события  или бифуркационного процесса  и пусть в результате свершения этого события или процесса система приобрела некоторое -тое состояние. Какова вероятность того, что до свершения события или процесса система находилась в -том состоянии. Эта вероятность может быть определена как вероятность перехода из -того состояния в -тое, делённая на суммы вероятностей перехода в -тое по всем-тым состояниям.

. .

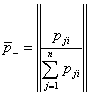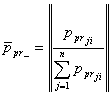Две последние матрицы являются в некотором смысле трансформированными матрицами к матрицам перехода. Матрицы, обратные к этим матрицам, также имеют некоторый физический смысл., так как преобразуют вектор вероятности прошлого в единичный вектор реализации настоящего.

Таким образом, сформирована квазигруппа вероятностных матриц, обладающих специфическими свойствами, отличающими их от классических матриц. Изучение свойств этой квазигруппы и анализ её подгрупп явится одним из основных положений теории Synergonet.

 

Литература.

 

1. Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

2. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168 с.

3. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. СПб.: Норма. 2002. 144 с.

4. Басин М. А., Шилович И. И. Синергетика и Internet. (Путь к Synergonet). СПб.: Наука. 1999. 71 с.

5. Басин М. А., Шилович И. И. Путь в Synergonet. СПб.: Норма. 2004. 128 с.

6. Басина Г. И., Басин М. А. СПб.: Синергетика. Эволюция и ритмы Человечества. Норма. 2003. 260 с.

7. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.

8. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с.

 

 

 

 

 

Этюд 41.

 

Человечество. Synergonet.

 

Кратко остановимся на результатах применения синергетической методологии к изучению некоторых проблем динамики человеческого общества [1]. Одними из главных свойств живых объектов являются их рост и размножение, тесно связанные между собой. В качестве параметра целого при математическом описании элементов триады: клетка-человек-человечество – нами была принята масса. Это позволило с единых позиций рассмотреть динамические процессы на различных уровнях масштабной иерархии и предложить для совместного анализа роста и размножения клеток и роста организма единую математическую модель, представляющую собой комбинацию итерационного процесса для степенных функций комплексного переменного и нелинейного дифференциального уравнения. Эта модель позволяет, в отличие от существующих стандартных моделей, одновременно учесть рост и размножение клеток организма. Предложенная модель может быть легко модифицирована и обобщена на различные типы ветвящихся процессов, каждый участник которых обладает двумя свойствами – роста и деления. Модель содержит три управляющих параметра, которые могут изменяться на каждом шаге размножения, что позволяет учесть влияние внешних условий на динамику размножения и роста. (Авторы благодарят Р.Г. Баранцева за ценные рекомендации по усовершенствованию предложенной модели) [1], [2].

 Для описания динамики параметра целого человеческой популяции, имеющей иной закон зависимости изменения массы от времени, нами была предложена математическая модель, использующая комплексные переменные, анализ которой позволяет не только предсказать гиперболический рост человеческой популяции, наблюдавшийся на этапе демографического взрыва, но и демографический переход, соответствующий  наступающей в настоящее время стабилизации количества людей. Комплексификация модели позволила наряду с результатами, полученными ранее С. П. Капицей [3], проанализировать новое уравнение, которое, в соответствии с нашим предположением, описывает динамику изменения информационного параметра человеческой популяции. В соответствии с исследовавшейся моделью в настоящее время человечество переживает процесс, называемый демографическим переходом, когда интенсивный рост числа людей сменяется стабилизацией, сопровождающимся кризисами, в том числе и экономическими. Можно предположить, что наблюдающийся сейчас экономический кризис является проявлением происходящего в настоящее время качественного изменения динамики роста человеческой популяции. Однако, исследованная модель соответствует лишь одному из возможных будущих сценариев динамики человеческой популяции. В настоящее время могут быть рассмотрены ещё два возможных сценария динамики: резонансная (пессимистическая) модель, поддерживаемая экологами, соответствующая катастрофическому или плавному сокращению числа людей, истощивших ресурсы Земли и не нашедших альтернативных источников существования; космическая (сверх - оптимистическая) модель соответствующая выходу человечества за пределы Земли, а затем и Солнечной системы [1].

 Проекция рассмотренной выше триады [4, 9](Смотри этюд №9)

                                                     Поле

                                                     /           \

                                        Структура - Контроллер

 

 на человеческое общество может выглядеть следующим образом:

                                                        Космос

                                                     /               \

                   Человеческая популяция – Государство.

   

Космос – поле человечества, включает ближнее поле – планету Земля. В качестве дальнего поля можно рассматривать Солнечную систему и даже всю Галактику.

    Человеческая популяция – совокупность людей совместно с их  собственностью, понимаемая как некий материальный объект.

    Государство – под этим термином мы понимаем контроллер человеческой популяции - систему, управляющую взаимоотношениями между людьми и связями человечества с внешней средой - Космосом.

    Эта системная триада может быть дополнена связанной с ней триадой взаимодействия, действующей на стыках элементов основной триады:[1, 4]

                                                    Тело   -   Дух

                                                          \         /

                                                          Душа

     Тело - это процессы материального взаимодействия Человечества с окружающей природой, в результате которых обеспечиваются все элементы материального существования человечества как биологического вида. Сюда относятся, в основном, процессы обмена материей и энергией.

    Душа – результат взаимодействия контроллера человечества, условно названного нами         государством, с естественно выстраивающейся социальной иерархической системой, формируемой   отдельными людьми и их группами.

    Дух - процессы взаимодействия контроллеров человечества и Космоса – окружающей среды – своего рода совместный творческий потенциал человечества и Космоса.

Введённые триады могут быть объединены в единую схему[1].

    Аналогичная система двух связанных триад может быть построена и для отдельного человека:

                                              Внешняя среда человека

                                            /                                            \

                            Организм человека - Управляющая система

 

    Внешняя среда человека – объекты, определяющие жизнедеятельность отдельного человека, в том числе и люди, составляющие часть человечества или всё человечество. В последнее время такой средой всё больше становится Synergonet.

    Управляющая система – контроллер, осуществляющий управление взаимодействием организма    человека с внешней средой и внутренней жизнедеятельностью человека.

    Организм человека – материальная часть человека как системы.

    К этой триаде примыкает двойственная ей триада взаимодействия:

 

                                   Обмен веществ - Интеллект –

                                         \                               /

                                     Управление организмом.

   

    Обмен веществ – материальный обмен человека и внешней среды веществом и энергией.

    Интеллект – информационный обмен человека с внешней средой, управляемый, в основном, нервной системой, в том числе и общение между людьми,      Управление организмом – управление процессами, обеспечивающими целостность организма, осуществляемое, главным образом, эндокринной системой.

Две последние триады также  могут быть объединены в единый комплекс.

    Аналогичные связанные триады могут быть построены и для отдельной клетки:

                                                   Внеклеточная среда

                                                   /                                \

                                           Структура клетки – Геном

 

          Внеклеточная среда – внутренняя среда организма, состоящая из других клеток и межклеточной среды.  Для клеток кожи – это также внешняя среда человеческого организма.

           Контроллер клетки, содержащий информацию о структуре клетки и во многом о структуре организма в целом.

     Структура клетки – материальная часть клетки, в которой осуществляется обмен веществом и энергией.

    Так же, как и ранее, может быть выстроена дополнительная триада взаимодействия, включающая:

 

                                        Питание---------- Информационный обмен

                                                         \                   /

                                     Управление внутренним обменом

    Питание - энергетический материальный обмен клетки с другими клетками и системами, обеспечивающими жизнедеятельность организма.

    Управление внутренним обменом – процессы управления внутренней жизнедеятельностью клетки.

    Информационный обмен - обмен информацией между контроллерами клетки и организма.

 Две последние триады также могут быть объединены в целостный комплекс.     Между построенными комплексами существуют связи, наличие которых позволяет говорить о спирали резонансных взаимодействий элементов различных масштабных уровней.

     Организм человека является основной частью поля отдельной клетки, тогда как человеческая популяция является основной частью поля отдельного человека. Особую роль играют связи контроллера клетки – генома со структурой человеческого организма, а, возможно, и с динамикой развития человеческого общества. Однако, не менее важны резонансные связи между контроллерами клетки, организма и человечества в целом – то есть связи между геномом, нервной и эндокринной системами и информационными структурами, создаваемыми человечеством. Геном клетки резонансно и достаточно жёстко определяет её структуру и структуру человеческого организма, в том числе и структуру эндокринной и нервной системы. Однако нервная система человека неоднозначно определяет структуру человеческого общества. Обратное же влияние внешнего поля на геном человека считается пренебрежимо малым. С таким утверждением трудно согласиться. Если изменения, происходящие с контроллером отдельного человека, практически не влияют на геном половых клеток, то длительные изменения внешней среды, поля, в котором существует человечество как вид, за счёт масштабного резонанса должны вызывать приспособительные изменения генома не только за счёт отбора случайно приобретённых признаков. Эта  проблема требует своего решения именно в настоящее время, так как развитие человечества привело к резкому изменению состояния ближнего поля – биосферы и поверхности Земли, что в свою очередь за счёт обратных связей может привести к изменению генома человека.

В динамике клетки, человеческого организма и человечества всё более возрастающую роль играет информационная составляющая взаимодействия, изучение которой потребовало введения таких понятий как      бифуркационное событие, то есть событие, имеющее дискретное или континуальное множество потенциально возможных исходов; бифуркационный процесс, представляющий последовательность бифуркационных событий. Введение этих понятий потребовало модификации существующих представлений об энтропии и информации сложных систем. Наряду со стандартным определением количества информации как меры уменьшения неопределённости рассмотрено представление об информации как результате отождествления состояний, структур и событий. Наряду с представлением об информации о прошлых событиях введено представление об информации о будущем – знании, которое базируется на отождествлении нескольких аналогичных событий. Введено двухпараметрическое рассмотрение энтропии и информации сложной системы,        использование которого позволило установить многосторонние связи между информационными характеристиками системы и границами раздела сред .[5]

Приближённое графическое представление последовательности связанных между собой бифуркационных событий мы назвали графом структур и событий. У исследуемой системы можно выделить периоды, характеризуемые двумя характерными типами поведения

    а) Периоды сравнительно плавных изменений, когда система приближённо может быть описана как детерминированная и для её описания пригодны методы теории динамических систем (русла в терминологии Г. Г. Малинецкого). Этим периодам соответствуют рёбра графа структур и событий.[6]

 б) Периоды резких бифуркационных изменений, в результате которых система может с некоторой вероятностью приобрести одно из множества возможных состояний  – бифуркационные события (джокеры в терминологии Г.Г. Малинецкого [6]).

 Качественный и количественный анализ графа структур и событий показал, что кроме структурной проекции, характеризуемой триадой параметров (мерой, типом классификации, иерархией), необходимо рассматривать бифуркационную проекцию графа, включающую в себя различные возможные варианты  поведения системы. Именно заполнение этой проекции определяет развитие информационной составляющей динамики человеческого общества.

Для того, чтобы выжить в мире, который не только даёт пищу, воду и воздух, но и приносит природные катастрофы, внутренние раздоры, болезни, врагов и конкурентов, необходимо уметь предсказывать грядущие опасности. Для решения этой проблемы природа наделила каждого человека самым мощным среди животных гомеостатическим контроллером – развитой нервной системой. В процессе развития человечества всё большую роль начинали играть не только непосредственное получение информации, но передача полученной информации другим людям, а также её переработка. Развитие звуковой речи характеризовало очень глубокий уровень переработки информации. Для того, чтобы назвать какой-либо объект, необходимо было не только выделить его из окружающего мира, но и включить в качестве кванта в некоторую обобщённую волну, всем квантам которой было присвоено одно и то же имя, один и тот же символ. Одновременно с возникновением речи был сделан первый шаг к созданию отличной от генетической общечеловеческой памяти – создание каменных скульптур и наскальных изображений, явившихся прообразом изобразительного искусства, сохраняющего образную информацию вне человеческого мозга. Следующим шагом в отчуждении информации от отдельного человека  и передаче её общему контроллеру человечества было изобретение письменности - этой задержанной на долгое время речи. Появились новые символы -  символы символов – цифры, буквы и иероглифы. Так возникла         первая символьная память, носителем которой стал не отдельный человек, а некий меатериальный объект, пользоваться которым мог любой человек, умеющий читать (т.е. знающий код). Появилась и стала интенсивно развиваться индустрия вне-мозгового сохранения словесной информации. Письменность – это гигантский скачок в формировании контроллера человечества как единой волны, так как с её появлением впервые появилась потенциальная возможность создать носители существенно переработанной информации, необходимой для всего человечества, позволяющие длительно хранить эту информацию вне человеческого мозга. Развитие письменности и создание хранилищ рукописей явилось важнейшей формой сохранения общечеловеческой информации – мудрости человечества. Именно в Священных книгах хранились основные положения всех древних религий и учений. Возникла возможность появления почты, передачи письменной информации на произвольные расстояния. Одновременно со средствами запоминания и передачи информации развивались и средства сжатия общечеловеческой информации и превращения её в знание, которое началось с появления языка. Проявлениями этого процесса явились создание и запоминание религиозных учений, в которых сохранялась память о приобретённых ранее знаниях и на их основе давались рекомендации на будущее, определялась мораль человеческого общества – правила взаимоотношения людей, обеспечивающие их совместное выживание. Существенную роль в этом процессе сыграло появление научного знания – то есть отыскание общих качественных и количественных закономерностей окружающего мира и человеческого общества. Следующим важнейшим шагом в развитии информационных структур явилось изобретение книгопечатания – появилась не существовавшая до этого момента возможность создания неограниченного числа копий наиболее важных для отдельных людей литературных и научных произведений. XIX и XX века. принесли человечеству поток новых средств передачи и хранения информации: фотография, телефон, телеграф, радио, телевидение, аудио- видео- аппаратура, компьютеры, мобильные телефоны. При этом всё большую и большую роль стали играть запоминание звуковых и визуальных образов, что значительно изменило форму информационных потоков, циркулирующих в человеческом обществе. Затем появился Internet. Функционирование Internet первое время       практически не сказывалось на потоке информации, циркулирующей в человеческом обществе, и влияющей на его поведение. Однако сегодня Internet - это уникальная глобальная информационная система, управляющая большей частью информации, циркулирующей в человеческом обществе. Развитие Internet является в настоящее время индикатором изменений контроллера человечества. Анализ  динамики её развития позволяет изучить процессы резонансной самоорганизации контроллера человечества и превращения его в принципиально новую структуру, названную М.  А. Басиным и И. И. Шиловичем - Synergonet.[7][8]

Проследим вслед за ними некоторые этапы на пути в Synergonet:

 1 Стандартный компьютер с момента своего появления являлся одним из средств преобразования информации. Компьютерные программы содержат некоторые необходимые для предсказания будущего полученные ранее  исходные данные и детерминированный алгоритм преобразования их в другие данные, необходимые для построения элементов будущих процессов, входящих в граф структур и событий. Первоначально компьютеры были использованы лишь для значительного ускорения рутинной вычислительной работы по преобразованию полученных человеком данных из одной формы в другую, более удобную для практических задач.

2. Компьютерная память – второй этап в процессе передачи информационных потоков компьютерным системам. Компьютер принимает на себя функции библиотеки концентрированной информации.

 3. Появление первых сетей – сначала в архитектуре компьютера для реализации принципа многозадачности разделением времени решения. Затем появление сетей, обеспечивающих информационное взаимодействие многих людей, коллективов, их компьютеров и корпоративных сетей при решении всё более сложных задач. Фактически этот третий этап продолжается и в настоящее время в процессе развития Internet. Однако данный процесс имел два основных под-периода, отличающихся объёмом включения в процессы развития сетей случайного элемента и порождение новых связей между людьми. Первые связи между компьютерами были практически детерминированы и определялись связями между людьми, которые существовали и до введения компьютеров.

 4. Существенное принципиальное значение того, что произошло с развитием Internet, это то, что в компьютерный мир был внедрён рынок – с атрибутами самоорганизации. При этом впервые возникло глубокое обратное влияние Internet на связи между людьми, в частности, на их экономические отношения. Cейчас уже говорят о том, что торговля через Internet скоро полностью заменит другие формы торговли.  

5.А это, в свою очередь, меняет структуру человеческого общества и является первым шагом к формированию принципиально новой структуры, – Synergonet.  Synergonet - результат совместной резонансной самоорганизации человечества и Internet., приводящей к качественному изменению контроллера человеческого общества, а следовательно и самого общества. Интенсивное развитие сети мобильных телефонов и происходящее в настоящее время их резонансное объединение  с Internet – одно из свидетельств этого процесса.

6. Synergonet берёт на себя во всё большей мере роль глобального контроллера , забирая всё больше функций у человеческого мозга  и Государства. Все информационные ресурсы переносятся в Synergonet. Возникает проблема управления при помощи Internet производственными процессами и решением политических и социальных проблем.

7. При этом возникает опасная для человечества перспектива возникновения Synergonet 2.[7][8].  Сеть может приобрести свой собственный внутренний контроллер, целью которого может стать выживание Сети, не обязательно дружественный контроллеру человеческого общества. Изучение  проблемы сознания Сети в настоящее время представляется нам особенно важным. Ведь нынешний глобальный структурный кризис совпал по времени с третьим бифуркационным кризисом Internet, связанным с переходом системы Internet–Человечество в фазу Synergonet, предсказанным М.А. Басиным и И.И. Шиловичем ещё в 1999 году.

 

Литература

 

1. Басина Г. И., Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с.

2. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000. 168 с.

3. Капица С. П. Общая теория роста человечества: сколько людей жило, живёт и будет жить на Земле. М.:.Наука.1999.190 с.

4. Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.

5. Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144с.

6.  Управление риском: Риск. Устойчивое развитие. Синергетика. М.: Наука. 2000. 431 с

7. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71с.

8. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.

9. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма.2006. 56 с.

 

Басина Г. И., Басин М. А.

НИЦ «Синергетика» Санкт-Петербургского союза учёных.

Этюд 42.

Синергетика.

Число Хавинсона. Комментарий.

 

18 октября 2011 года в рамках программы «Академия» на телеканале «Культура» профессор В.Х. Хавинсон прочёл лекцию о последних успехах геронтологии. В частности, он сообщил о своих последних результатах, указывающих на важную роль пептидов в  проблеме продления жизни.

При этом им был обнаружен замечательный факт, что предельное увеличение продолжительности жизни, которое можно получить, равно примерно 42 процентам . При этом аналогичная цифра встречается в различных сериях экспериментов. Это число может быть названо числом Хавинсона. Механизм появления этого числа В.Х. Хавинсону неизвестен.

 В настоящем этюде будут высказаны гипотезы, проверка которых, возможно, прольёт свет на  механизм появления числа Хавинсона.

Несколько модифицируем это число.

Использование пептидов даёт предельное продление жизни организма приблизительно в 1.42 раз.

А это число  очень близко к известному в математике числу – корню из двух - 1.41421.

Если предположить идентичность модифицированного числа Хавинсона и корня из двух, то можно построить приближённую синергетическую модель работы пептидов, которая может быть проверена экспериментально. Корень из двух – это гипотенуза равнобедренного прямоугольного треугольника со стороной, равной единице. Следовательно, гипотеза должна быть геометрической. Можно предположить, что  соединение пептидов с генами имеет два предельных состояния, отличающихся геометрией соединения. При этом второе предельное состояние требует вдвое большего количества пептидов, расположенных по отношению к гену под углом в 45 градусов и следовательно в корень из двух раз менее эффективными. Тогда суммарная эффективность удвоенного количества пептидов будет в корень из двух раз больше, чем в первом состоянии.

Эта гипотеза должна быть проверена экспериментально.

 

 

                                                                     Этюд 43.

 

                                   О современном этапе развития человечества

.

 

.В середине 80-х годов человечество вступило в эпоху демографического перехода. Гиперболический рост числа людей, продолжавшийся в течение миллиона лет, сменился периодом стабилизации числа членов человеческой популяции. Начался период глобализации, сопровождающийся такими качественными изменениями в структуре общества, каких не было за всё время существования человечества. Человечество похоже сейчас на молодого человека, вступающего в этап зрелости.

Глобализация многолика: это и интенсивное развитие научных исследований, и создание и развитие принципиально новых технологий, базирующихся на глубоком проникновении в микромир, и беспрецедентное усиление международных связей, и появление и взрывное развитие такого феномена к ак Internet, которая проникает в каждый дом и всё больше становится похожей на нервную систему (контроллер) человечества, которую мы назвали Synergonet, и всё большая интеграция мировой экономики. Всё это приводит интегрально к увеличению срока жизни каждого отдельного человека.

Но глобализация влечёт за собой новые угрозы и опасности, связанные с тем, что в руках у человека оказались силы , соизмеримые с силами Природы, и неизвестно , хватит ли у людей духовности, разума, воли, чтобы позитивно распорядиться этими силами. Атомное оружие и атомные электростанции, СПИД и наркотики, экологические проблемы, ксенофобия, неограниченное стремление к власти и наживе, не уменьшающееся, и даже растущее социальное неравенство,- вот только некоторые угрозы, которые не только не уменьшаются, но растут с глобализацией.

         Характерным примером глобальных качественных изменений стал недавний экономический кризис, главным уроком которого стало понимание мировой экономической и политической элитой того факта, что окончился не только период неограниченного роста числа людей, но и период безудержного роста экономики.

А это должно изменить философию экономики и политики, ограничить произвол как администраторов, так и предпринимателей и финансистов, стимулировать развитие международных правовых норм, что позволит разрешать  конфликты мирового сообщества на правовой основе, свести к минимуму или вовсе избежать военных конфликтов.

Различные страны вступают в новую эпоху с различным уровнем качества жизни, экономики, различным политическим устройством. И этот уровень определяет то место, которое займёт страна в структуре будущего социального устройства, - будет ли она занимать достойное место в международной иерархии, или останется на задворках истории или вообще исчезнет  как самостоятельная культурная и экономическая единица.

Именно эта проблема стоит в настоящее время перед Россией.

В отличие от многих других стран Россия занимает гигантские пространства на двух континентах, располагаясь между Азией и Европой. Большие пространства одновременно являются и благом и недостатком. Благо- это гигантские возможности использования невозобновляемых и возобновляемых природных ресурсов. Недостаток состоит в том, что большая часть страны имеет неблагоприятные климатические условия и требуется повышенный расход энергии.

В прошлом, для удержания и захвата новых земель требовались значительные затраты на вооружение. Это во многом определяло диктаторский характер Российского правительства, не зависимо от того, как оно называлось: монархия или коммунистическое правление. И хотя в последнем случае стремление создать самое мощное в мире оружие привело к развитию научных исследований и созданию современной военной техники, однако, в конце концов, этот путь привёл к краху коммунистического режима в России.

Поэтому Россия пережила за короткий срок не один а три экономических кризиса

В середине первого из них выдающийся Российский учёный , спасший мир от ядерной катастрофы, Никита Николаевич Моисеев в докладе на Международном синергетическом Форуме поставил вопрос о том, с чем должна Россия войти в Новое мировое сообщество.

Он считал, что главными являются три идеи:

1.    Национальная идея России

2.    Богатый научный потенциал

3.    Транспортная артерия между Востоком и Западом

     Следует отметить, что он отмёл как временное преимущество использование невозобновляемых природных ресурсов.

К трём пунктам Н.Н. Моисеева нам хотелось бы добавить ещё один: возобновляемые природные ресурсы, при этом для России особую роль играют лесные массивы..

С момента выступления Н. Н. Моисеева прошло 15 лет. Что же произошло? Мы по-прежнему живём за счёт невозобновляемых природных ресурсов: нефти, газа, металлов, и строим свой бюджет на высокой цене на нефть. Именно поэтому во время глобального кризиса падение производства в России оказалось значительно сильнее , чем в большинстве развитых стран.

С национальной идеей России оказалось тоже не так хорошо, как хотелось бы. На первый взгляд, кажется, что распад страны приостановлен. Начинает проводиться взвешенная национальная политика. Но это только кажется. Ксенофобия всё больше проникает в массы и иногда прорывается в виде террористических актов и национальной ненависти. Чёткой национальной идеи так и не выработано.

Богатый научный потенциал в некоторых областях фундаментальной и прикладной науки, связанных с гонкой вооружений, носивший односторонний характер, позволил создать мощный военно - промышленный и научный центр, подготовить специалистов высочайшего класса, добиться выдающихся успехов в космосе и атомной промышленности, военном кораблестроении и авиастроении. Однако, развитие страны было односторонним, что привело к катастрофе.Научно-промышленный комплекс, обеспечивавший военный паритет Коммунистического Советского Союза, позволивштй добиться значительных успехов в области космических исследований, авиации и судостроения, а также создать мощную атомную энергетику в условиях непрекращающихся кризисов не смог полностью перестроться на мирные рельсы. Мощная иерархическая система Советской науки , включавшая как замечательные научные школы так и иерархию партийных функционеров-администраторов, начала размываться. Молодые учёные либо уехали за границу либо ушли в бизнес. Многие научные достижения либо устарели, либо были потеряны. США и Израиль, научная элита которых пополнилась выдающимися представителями Советской науки, совершили гигантский технологический скачок. Только сейчас власти России спохватились. Оказывается, только высокие технологии, базирующиеся на прекрасно финансируемых фундаментальных и прикладных научных исследованиях, могут обеспечить конкурентоспособность страны в мировом экономическом процессе.    

 

 

 

 

 

Рейтинг@Mail.ru