Синергетика.
Этюды 70.
Посвящено
100-летию со дня рождения выдающегося учёного, профессора
Басина Абрама Моисеевича.
Басина
Г. И., Басин М. А.
НИЦ
«Синергетика» Санкт-Петербургского союза учёных.
Этюд 8
Ещё
раз о природе времени
23 февраля
2011г.
Одной из вечных загадок природы является время – параметр, который определяет всё наше существование, течение которого происходит, казалось бы, независимо от нас. При этом нам кажется, что мы можем измерять поток времени и даже управлять его течением. Характерным свойством времени является его необратимость. В реальной жизни мы не можем вернуться в прошлое. Это можно сделать лишь мысленно, в нашей памяти. Существует реально лишь один момент времени – настоящее, в который мы осуществляем некоторые действия. Всё, что было до этого, уже прошло и оставило свои следы в нашей памяти, в нашем нынешнем состоянии, в окружающей нас природе. Всё, что будет, является для нас не вполне определённым, то есть таким, что может быть нами однозначно предсказано и обязательно достигнуто. Будущее не является фатальным, а хотя бы частично зависит от наших желаний и нашей воли. Это свойство может быть названо необратимостью времени. В отличие от пространства, в каждое место которого мы, в принципе, можем вернуться, вернуться в прошлое, насколько нам известно, не удавалось никому. При математическом описании процессов окружающего мира время является основным параметром, характеризующим динамику изменения состояний различных структур и систем. При этом выделяются два типа процессов.
Процессы, практически обратимые во времени, будущее поведение структур и систем в которых, в принципе, может быть предсказано однозначно. Такие идеальные процессы описываются при их моделировании, например, законами Ньютона для консервативных систем или обобщающими их уравнениями Шредингера для квантовой физики. Фактически для таких процессов время в нашем обыденном понимании вообще не течёт. Оно как бы исчезает, становится мнимым. Модели таких процессов описывают большое количество явлений окружающего мира. Утверждалось, что они всеобщи, во всяком случае, для неживой природы.
Это утверждение противоречит необратимому характеру процессов, происходящих с живыми организмами, в частности, с каждым из нас. Однако и сама необратимость процессов также двояка. Процессы с течением времени могут деградировать, а могут развиваться, охватывая все большее количество структур и систем. При этом законы деградации и законы развития существенно отличаются друг от друга.
Особое внимание следует обратить также на характер нашего восприятия настоящего, прошедшего и будущего времени. Мы можем ощущать только настоящий момент времени, тот, в который мы существуем. Этот момент как бы скользит с определенной скоростью по шкале времени, совпадая с моментами, которые были для нас будущими, и затем оставляя их в прошлом, к которому мы можем вернуться только в своей памяти. Это ещё одно проявление необратимости времени.
Закономерности протекания тех или иных процессов во времени и в пространстве мы можем выразить математически с помощью изучения уравнений движения и их решений. Так, например, обратимые процессы выражаются математически в виде решений обыкновенных дифференциальных уравнений для положения структуры в пространстве или волновых уравнений для некоторых функций и потенциалов.
Однако
существуют дифференциальные уравнения в частных производных, некоторые решения
которых принципиально несимметрично зависят от времени. Это параболические
уравнения, простейшим частным случаем которых является одномерное уравнение
теплопроводности.
![]() (1)
(1)
Мы считаем, что подробный анализ его фундаментального
решения может пролить новый свет на природу зависимости процессов окружающего мира
от времени. Фундаментальное решение уравнения теплопроводности даётся формулой
Пуассона [1]
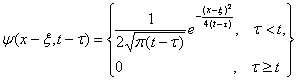 , (2)
, (2)
где функция, ![]() , описывающая процесс, несимметрична относительно момента
измерения
, описывающая процесс, несимметрична относительно момента
измерения ![]() (настоящего момента).
До этого момента она считается равной нулю. В завершение настоящего момента она
представляет собой дельта - функцию Дирака, которая затем диффундирует,
сохраняя неизменным и равным единице
интеграл, взятый вдоль оси x.
(настоящего момента).
До этого момента она считается равной нулю. В завершение настоящего момента она
представляет собой дельта - функцию Дирака, которая затем диффундирует,
сохраняя неизменным и равным единице
интеграл, взятый вдоль оси x.
Это
свойство решения уравнения теплопроводности позволяет интерпретировать его как
распределение вероятности реализации того или иного события и считать его
описывающим математически деградационные процессы, происходящие в природе. Оно
же является символом второго закона термодинамики – закона роста энтропии. В
пределе при очень больших положительных значениях времени фундаментальное
решение (2) при всех значениях координаты стремится к нулю, сохраняя интеграл
равным единице. Время в этом случае выполняет роль меры деградации родившейся в
момент ![]() структуры. Следует
обратить внимание на то, что на отрицательной шкале относительного времени
структуры. Следует
обратить внимание на то, что на отрицательной шкале относительного времени ![]() функция
функция ![]() , описывающая состояние системы, равна нулю. Система как бы
рождается из ничего в момент
, описывающая состояние системы, равна нулю. Система как бы
рождается из ничего в момент ![]() и далее начинает
деградировать, сохраняя некоторый инвариант. Но рождение из ничего противоречит
нашим представлениям о природе. Всё новое рождается из чего-то старого. Как можно
в данном случае найти это старое?
и далее начинает
деградировать, сохраняя некоторый инвариант. Но рождение из ничего противоречит
нашим представлениям о природе. Всё новое рождается из чего-то старого. Как можно
в данном случае найти это старое?
Будем считать, что функция, описывающая
процесс, должна аналитически продолжаться в область отрицательных значений
моментов времени. Для этого можно формально подставить в формулу Пуассона (2)
отрицательные значения относительного времени![]() .
.
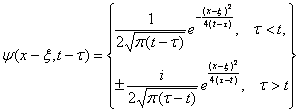 (3)
(3)
Формула (3) обладает следующими свойствами.
Первое
свойство состоит в том, что динамическая функция ![]() при отрицательных значениях относительного времени перестаёт
быть действительной величиной. Реальная часть этой функции обращается в нуль,
как и в выражении (2).
при отрицательных значениях относительного времени перестаёт
быть действительной величиной. Реальная часть этой функции обращается в нуль,
как и в выражении (2).
Во-вторых, появляется мнимая часть, которая может иметь два значения, отличающиеся знаком.
В третьих, необычным оказывается поведение получившейся
функции в зависимости от координаты. Минимальное значение она имеет при ![]() =0, то есть в точке, в которой при положительных значениях
относительного времени рождается новая реальная структура. С увеличением модуля
координаты эта мнимая функция растёт как экспонента квадрата координаты.
=0, то есть в точке, в которой при положительных значениях
относительного времени рождается новая реальная структура. С увеличением модуля
координаты эта мнимая функция растёт как экспонента квадрата координаты.
В четвёртых, рост этой функции от времени при приближении к
моменту ![]() также происходит
чрезвычайно быстро, здесь возникает неинтегрируемая особенность.
также происходит
чрезвычайно быстро, здесь возникает неинтегрируемая особенность.
В пятых, при всех значениях ![]() , приближаясь к моменту «рождения» структуры, мнимая часть
функции стремится к бесконечности.
, приближаясь к моменту «рождения» структуры, мнимая часть
функции стремится к бесконечности.
При этом переход через точку ![]() = 0 во всех местах, кроме
= 0 во всех местах, кроме
![]() =0, обращает действительную и мнимую части комплексной
характеристической функции
=0, обращает действительную и мнимую части комплексной
характеристической функции ![]() в нуль. Создаётся впечатление, что момент
в нуль. Создаётся впечатление, что момент ![]() = 0 является мощным барьером, около которого концентрируется
некий мнимый потенциал, интенсивность которого растёт по мере удаления от точки
рождения реальной структуры.
= 0 является мощным барьером, около которого концентрируется
некий мнимый потенциал, интенсивность которого растёт по мере удаления от точки
рождения реальной структуры.
В самом слабом месте, вблизи точки ![]() =0 этот потенциал как бы рождает и выталкивает реальную
структуру в область реального положительного относительного времени, где она
существует, деградируя во времени и диффундируя в пространстве. Если предположить,
что ось времени замыкается на бесконечности, то функция, переходя на
бесконечности через нуль, возвращается обратно уже в виде пары интенсивно
растущих мнимых функций. Круг замыкается.
=0 этот потенциал как бы рождает и выталкивает реальную
структуру в область реального положительного относительного времени, где она
существует, деградируя во времени и диффундируя в пространстве. Если предположить,
что ось времени замыкается на бесконечности, то функция, переходя на
бесконечности через нуль, возвращается обратно уже в виде пары интенсивно
растущих мнимых функций. Круг замыкается.
Попытки найти в природе некоторые аналоги подобного поведения реальных структур и систем приводят нас к выводу, что нечто подобное происходит в живой природе. Из огромного количества семян, число которых резко возрастает к моменту созревания, рождается одно реально существующее растение, которое затем, погибая, вновь рождает огромное количество семян. Конечно, жизнь намного сложнее простейшей математической модели, описанной нами выше, однако качественное описание процесса рождения рассмотренная нами модель даёт.
Нечто подобное наблюдается при теоретическом исследовании зарождения и диффузии вихрей в вязкой жидкости. Вихревые потоки рождаются сингулярно в зонах неоднородностей и на границах жидкости, а затем диффундируют в соответствии с уравнением теплопроводности внутрь жидкости.
Мнимость характеристической функции при отрицательных значениях относительного времени, возможно, свидетельствует о том, что эта функция характеризует некоторые информационные процессы. Например, в классической триаде Р. Г. Баранцева [2] она может отвечать за «интуицио». Так, в результате «озарения» после усиленного мысленного напряжения рождается новая идея.
В пользу целесообразности выполненного нами анализа и возможности нахождения его реальных аналогов говорит следующее очень важное обстоятельство.
Мы можем наряду с действительным рассматривать и мнимое время. В этом случае уравнение теплопроводности превращается в уравнение Шредингера для свободной частицы, а его решение характеризует волновую функцию сохраняющейся во времени перемещающейся в пространстве свободной элементарной частицы [3]. По утверждению основоположников квантовой механики, это уравнение и его частный случай: уравнение Ньютона описывают все инерционные процессы в неживой природе, происходящие со скоростями, намного меньшими, чем скорость света. Если в него добавить ещё один член, отвечающий за потенциальные силы и учесть достижения теории относительности, в которой априори рассматривается мнимое время, то, по их мнению, можно описать все явления неживой природы.
Но введение мнимого времени является лишь естественным следующим шагом в нашем рассмотрении. То, что рассмотрение мнимого времени дало результат, который вместе со своими обобщениями практически описывает большую часть современных физических представлений, говорит о том, что и первый сделанный нами шаг имеет право на включение его в фундамент современной науки.
Следующим шагом должно быть рассмотрение фундаментальных решений уравнений с комплексным временем и комплексными координатами. Некоторые примеры эффективности подобного рассмотрения приведены в [4-10].
Возражения против выполненного анализа могут быть высказаны в связи с тем, что при стремлении относительного момента времени к нулю со стороны прошлого модуль мнимой части характеристической функции имеет неинтегрируемую особенность. Однако, это может свидетельствовать также о существовании некоторого малого (и одновременно очень большого обратного ему) параметра, характеризующего неопределённость настоящего момента времени и ограничение величины характеристического потенциала сверху. Этот параметр может быть связанным с постоянной Планка, а может быть и не зависимой от неё константой Природы.
Литература.
1.Михлин С. Г. Линейные уравнения в частных производных. Учебное пособие для вузов. М.: Высшая школа».1977. 431 с.
2.Баранцев Р. Г. Становление тринитарного мышления. М. - Ижевск: НИЦ «Регулярная и хаотическая механика» 2005. 124 с.
3. Каку М. Введение в теорию суперструн. М.: Мир .1999. 634с.
4. Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем Ч. 1. СПб: Норма. 2000.168с.
5.Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2.СПб: Норма 2002. 144с.
6. Басин М. А., Шилович И. И. Синергетика и Internet (Путь к Synergonet). СПб: Наука 1999. 71с.
7. Басин М. А., Шилович И. И. Путь в Synergonet. СПб: Норма 2004. 128 с.
8. Басина Г. И.,Басин М. А.: Синергетика. Эволюция и ритмы Человечества. СПб.: Норма 2003. 260 с
9. Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб: Норма. 2006. 56 с.
10. Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008. 144с