ДЕТЕРМИНИРОВАННЫЕ СТРУКТУРЫ С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ. ВОЗМОЖНОСТЬ КОМПЬЮТЕРНОЙ РЕАЛИЗАЦИИ.

УДК 167.0

© Басин Михаил Абрамович, д.т.н., профессор,

Директор научно-исследовательского центра "Синергетика" Санкт-Петербургского союза учёных.

Контакт с автором: basin@soft-tronik.spb.ru

Работа выполнена при поддержке РГНФ  (Грант № 03-03-00247a/Б)

 

 

Аннотация

В работе представлена модель изолированной детерминированной динамической структуры с конечным числом состояний. Показано, что структуры такого типа имеют аттракторы в виде стационарных точек или циклов. Максимальные аттракторы структур описываются математическими моделями, эквивалентными теории конечных групп. Построены различные формы представления динамики изучаемых структур.

 

1.Понятие детерминированной конечной системы.

Начнём математическое моделирование самоорганизующихся структур и систем с простейшего случая, который легко реализуется на компьютере. Предположим, что нам нужно создать простейшую математическую модель изолированной структуры, которая может потенциально существовать бесконечно долгое время [1].

Пусть совокупность обобщенных координат этой структуры составляет некоторый заданный список параметров, описывающих некоторое состояние. Для того, чтобы предлагаемая модель могла быть реализована на компьютере, число состояний структуры, соответствующих различным спискам, следует принять конечной величиной, равной .

Введём понятие автономной детерминированной динамической структуры (или динамического процесса ) с конечным числом состояний. Для этого предположим, что динамика изучаемой структуры описывается следующим образом: наряду с конечным числом списков (состояний) имеется однозначный не меняющийся в динамическом процессе оператор, отображающий одно состояние на другое.

Если ввести в рассмотрение замкнутую цепочку таких последовательных отображений, то процесс становится счётно-бесконечным. Автономная структура, описываемая таким модельным процессом, потенциально может существовать неограниченное время.

Если цепочка отображений такова, что процесс длится бесконечно, то в конце концов он выходит на один из списков, который был уже однажды пройден. С этого шага итераций (момента времени) процесс, описывающий динамику структуры, начинает повторяться – возникает цикл. Если при некоторой - той итерации список отображается сам в себя, то цикл вырождается в некоторое стационарное состояние, из которого автономная структура уже никогда не может выйти, если на неё не подействовать извне.

 

2. Обратимые детерминированные процессы с конечным числом состояний.

Рассмотрим первоначально взаимно однозначные отображения. В этом случае каждая однозначная функция , описывающая отображение множества списков на себя (оператор), имеет однозначное обратное отображение. Если мы пронумеруем все имеющиеся списки (элементы конечного множества списков) числами, то совокупность переходов от одного списка к другому, определяемая отображением , будет эквивалентна некоторой перестановке чисел. Тем самым, мы можем отождествить каждый из введённых нами операторов с элементом группы подстановок из списков (состояний). Эта группа в свою очередь эквивалентна конечной группе порядка [2].

Динамика автономной структуры, имеющей конечное число возможных состояний и определяемая взаимно-однозначным оператором , полностью описывается математической теорией конечных групп. Как известно, каждый элемент такой группы, соответствующий однозначному отображению , образует замкнутые циклические орбиты. Для заданного все списки (элементы множества списков) разбиваются на классы, внутри которых элементы могут циклически переходить друг в друга и не могут переходить в элементы другого класса. Все получающиеся таким образом циклы оказываются детерминированными и строго разделяют все множество списков (состояний). Каждый цикл оказывается автономным и можно считать, что ему соответствует динамика некоторой автономной структуры.

Обратимый алгоритм перехода, однозначно фиксирующий условия перехода из одного состояния в другое, действующий на конечном множестве списков и реализующий потенциально бесконечный процесс, может породить при своей реализации только модели динамических структур, всякое состояние которых бесконечное число раз циклически возвращается на круги своя.

 

3.Необратимые автономные детерминированные процессы с конечным числом состояний.

Пусть функция , являясь однозначной, не является взаимно-однозначной функцией. Тогда, применяя её на первой итерации (первом шаге по времени) к каждому элементу множества списков, в результате этой итерации получим, что число списков, которые будут участвовать во втором шаге динамического процесса, уменьшится. После конечного числа итераций произойдёт так, что -я итерация уже не уменьшит числа списков, и все дальнейшие итерации будут иметь дело с теми элементами, для которых функция окажется взаимно однозначной. Таким образом, из всех возможных состояний структуры (списков данных) в результате конечного числа итераций выделится (выживет) некоторая совокупность (подмножество) – максимальный аттрактор состояний, динамика которого эквивалентна динамике совокупности списков, определяемых взаимно однозначной функцией (конечное инерциальное многообразие) [3]. Будучи сужена на множество-аттрактор, функция становится взаимно однозначной.

Этот максимальный аттрактор может состоять из одного списка, и тогда формируемая им структура может считаться стационарной точкой.

Он может состоять также из единственного цикла, включающего все элементы аттрактора, тогда он может быть назван единственным аттрактором типа предельного цикла. Вся совокупность элементов (списков), задаваемых первоначально, в результате некоторого конечного числа итераций сходится к этому предельному циклу и может быть названа бассейном его притяжения.

Однако, предельная совокупность списков может сформировать, в свою очередь, несколько стационарных точек и циклов, каждый из которых определяет не только соответствующий ему класс списков, в нём участвующих, но и свой бассейн притяжения, то есть совокупность списков (состояний), которые в результате некоторой последовательности итераций сходятся именно к данному циклу (или стационарному состоянию) .

Для каждого числа списков (состояний), равного , может быть подсчитано общее число возможных функций и определена не только каждая из них, но и та динамическая система, которую она описывает.

А следовательно, теоретически или путём компьютерного моделирования может быть осуществлена полная классификация всех возможных функций на конечном множестве и всех автономных динамических систем с конечным числом элементов.

Так как каждой однозначной обратимой функции соответствует одна перестановка, то число таких функций определяется числом возможных перестановок из элементов и равно !

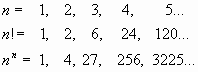
Совокупность набора списков (набора состояний) и однозначного детерминированного алгоритма переходов из одного состояния в другое формирует фазовое пространство модели, описывающей динамику автономной структуры. Фазовая траектория, характеризующая путь динамической системы в пространстве состояний, зависит от того состояния, с которого начинается движение (первая итерация).

В случае взаимно однозначной функции начальное состояние либо является стационарной точкой, либо принадлежит к некоторому циклу.

Каждый элемент группы перестановок конечного числа списков является аттрактором целого класса сжимающих не взаимно однозначных отображений для элементов, где .

Предположим теперь, что динамика автономной структуры с не взаимно однозначной отображающей функцией, реализована в виде некоторой программы на компьютере. Для каждого -того списка введём обозначение соответствующего ему состояния . Запустим нашу программу раз, задавая каждый раз различные значения . На первом шаге итераций число получившихся списков уменьшится. Этот процесс будет продолжаться до тех пор, пока на некотором шаге число списков, участвующих в итерационном процессе, не станет равным , после чего дальнейшее уменьшение числа списков прекратится.

Тем самым мы получим новую взаимно-однозначную функцию от элементов, оставшихся в динамическом процессе. Все остальные списки “вымрут”. Оставшееся множество списков и будет максимальным аттрактором.

Фазовое пространство детерминированной автономной структуры с конечным числом состояний может быть описано также направленным графом, узлы которого представляют состояния (списки или наборы данных), а линии определяют динамику отображений. При этом все пути этого направленного графа (фазовые траектории динамической системы) завершаются либо стационарными точками, либо циклами.

Каждый цикл имеет свой бассейн притяжения. В общем случае всё фазовое пространство разбивается на не связанные между собой направленные графы, каждый из которых кончается предельным циклом. Совокупность однозначных цепочек отображений разделяет все множество списков на предельные циклы и бассейны их притяжения, каждый из которых может рассматриваться как динамическая модель отдельной автономной структуры.

Внутри каждой такой модели , содержащей элементов мы можем выделить траекторий, начинающихся с каждого элемента множества списков. Все эти траектории обладают тем свойством, что, начиная с некоторого члена, своего для каждой траектории, динамика последовательности входит в аттрактор – цикл, единый для всех траекторий.

Начало движения определяется извне – некоей внешней системой, которая определяет начальный списoк (состояние). Можно считать, что начальный элемент списка определяется неким внешним контроллером [4].

“Бесконечность” процесса определяется внешним полем, в котором задается бесконечный натуральный ряд чисел, определяющий бесконечную последовательность итераций.

Таким образом, даже на этом – детерминированном уровне рассмотрения с конечным числом состояний динамическая система сдержит три элемента, которые в более сложных системах выявляются более рельефно.

Возможен ещё один способ описания систем такого типа. Совокупность возможных состояний системы может быть представлена в виде вектора состояний, компоненты которого принимают значения нуль и единица. Каждому состоянию системы соответствует при таком описании единичный вектор, компонента которого, соответствующая данному состоянию, равна единице, а остальные компоненты равны нулю. Алгоритм перехода из одного состояния в другое в этом случае описывается оператором в виде квадратной матрицы порядка , состоящей из нулей и единиц. Если структура описывается обратимой отображающей функцией, то матрица выглядит таким образом, что в каждой её строке и в каждом столбце оказывается по одной единице. Последовательное умножение таких матриц описывает циклический процесс динамики структуры.

Динамика любой детерминированной автономной структуры, принимающей конечное число состояний, может быть асимптотически описана некоторой периодической функцией от натурального ряда чисел. Путем сдвига нуля по номеру итераций в сторону больших значений номеров область её задания может быть расширена на все целые числа, как положительные, так и отрицательные.

Для внешнего описания такой структуры целесообразно ввести в рассмотрение внешнее поле с континуальным представлением о времени. В этом случае дискретный ряд последовательных событий перехода структуры из одного состояния в другое можно представить ступенчатой функциией от внешнего континуального времени, которое можно считать атрибутом поля. Из континуальной оси времени можно выбрать некоторую последовательность и каждому члену этой последовательности поставить в соответствие некоторое значение , равное номеру итерации в рассматриваемой нами динамической модели.

Промежутки могут быть как неравномерными, так и равномерными. Последнее означает, что динамика структуры синхронизирована с динамикой внешнего поля. В случае, когда - постоянная величина, номер итерации связан с соответствующим ему промежутком времени при помощи линейного соотношения . Последняя формула характеризует синхронизацию динамики структуры и внешнего поля. Введение внешнего времени позволяет описывать одновременно различные динамические процессы в одном внешнем поле.

Можно ввести в рассмотрение еще одну величину, характеризующую циклическую структуру, определяющую с точностью до масштаба число циклов, которое пройдено структурой с момента начала отсчёта, которое назовём действием структуры во внешнем поле. Предположим, что за прохождение одного цикла действие структуры изменяется на некоторую постоянную величину . Изменение действия структуры за циклов . Время прохождения структурой одного цикла определяется в случае постоянной величины по формуле , где - число шагов, соответствующих одному циклу. Общее время прохождения циклов

Откуда

. (1)

Если предположить, что в промежутке времени между шагами является гладкой функцией от , то

. (2)

Здесь - энергия цикла.

Параметру, характеризующему непрерывное изменение состояния автономной структуры (волновой функции) можно придать комплексную форму

(3)

Введём обозначение 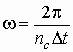- круговая частота цикла. Тогда получим связь между энергией и частотой цикла

. (4)

Любая детерминированная структура с конечным числом состояний является циклической и может быть описана функцией.

, (5)

где

- квант действия, соответствующий прохождению структурой одного цикла;

- энергия структуры, определяющая скорость прохождения цикла;

- число элементов в цикле;

- элементарный отрезок времени, соответствующий одному шагу процесса

В рамках нашего описания умножение и на можно принять в качестве действия некоторых операторов

. (6)

Применяя к функции оператор дифференцирования по переменной , получим

(7)

Это соотношение позволяет, по аналогии с квантовой механикой, отождествить оператор с оператором . В этом случае действие оператора можно расширить на любую функцию от и получить коммутационное соотношение.

или

……. (8)

Траектория структуры может быть представлена также отдельными точками на винтовой спирали единичного радиуса.

По оси спиральной линии будут отложены точки, которые характеризуют время, а длина спирали характеризует в некотором масштабе действие структуры. Отношение характеризует величину энергии структуры.

Таким образом, динамика детерминированных процессов с конечным числом возможных состояний может быть описана путём введения цепочки отображений друг на друга дискретных значений некоторой комплексной функции с модулем равным 1.

Однако, при желании более детально проанализировать сами состояния, в которых может оказаться структура, такое рассмотрение оказывается недостаточным.

Предположим, что среди состояний, моделирующих динамику структуры, имеется определённый класс состояний, переход между которыми определяется некоторым идентичным образом (например, переход от одного натурального числа к ближайшему). В этом случае для данного класса может быть установлен универсальный алгоритм перехода, который может быть описан единым образом, т.е. этот алгоритм не зависит от элемента, к которому он применяется. Тем самым, всё множество списков разбивается на классы, внутри каждого из которых действует свой универсальный алгоритм. Для некоторых элементов класса применение этого алгоритма приводит к тому, что результат выходит за пределы класса. Аналогично происходит и с вхождением в класс.

Рассмотрим первоначально взаимно-однозначную функцию. В этом случае внутри данного класса существует два типа траекторий:

1.      Проходящие траектории, которые входят и выходят из данного класса.

2.      Замкнутые внутри класса траектории – циклы.

Элементы класса (точки), в этом случае могут быть разделены на два типа:

а) внутренние точки.

б) граничные точки.

Граничные точки могут быть разделены на

а) входящие,

б)выходящие.

В частном случае, если входящая точка является одновременно и выходящей, то соответствующая ей проходящая траектория состоит из одной точки.

Если рассматривать динамику автономной структуры, описываемую не взаимно однозначной функцией, то число типов траекторий оказывается больше.

В этом случае не все входящие траектории выходят из данного класса. Часть из них, входя в класс, замыкается на некоторый цикл, часть имеет как входящие, так и выходящие точки. Кроме того, внутри класса могут находиться начальные точки траекторий, которые либо замыкаются на цикл, либо выходят из класса.

Динамика таких структур моделируется на любом стандартном компьютере в виде программ с единичным входом, содержащим циклы и метки. Меняя наборы данных и операторы , мы можем моделировать широкий класс детерминированных бесконечных циклических процессов.

Оператор перехода системы из одного детерминированного состояния в другое может быть комбинированным, состоящим из нескольких последовательно выполняемых операторов. В этом случае возникают промежуточные состояния, переход которых друг в друга зависит не только от исходного состояния, но и от того, какой элемент общего алгоритма мы реализуем. При этом на промежуточных стадиях возвращениe структуры к одному и тому же состоянию может стать нерегулярным. Однако в случае конечности шагов, на которые разбивается основной алгоритм и конечности числа возможных состояний , периодичность процесса , понимаемая теперь в более широком смысле сохраняется.

В компьютерной интерпретации это утверждение звучит таким образом.

Любая конечная детерминированная компьютерная программа, преобразующая любой конечный набор списков либо когда-нибудь остановится, либо будет периодически повторять один и тот же процесс.

 

Литература:

1.      Басин М.А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия структур и систем. Часть 2. СПб.: Норма. 2002. 144с.

2.      Чеботарёв Н. Основы теории Галуа. Часть первая. МЛ ОНТИ ГТТИ 1934. 222.

3.      Малинецкий Г.Г. Потапов А.Б. Современные проблемы нелинейной динамики. М.: Эдиториал УРСС, 2000. 336 с.

4.      Басин М.А. Волны. Кванты. События. Волновая теория взаимодействия структур и систем. Часть 1. СПб. “Норма” 2000. 168с.